第五单元: 面积(单元复习课件)-三年级数学下册 人教版(共40张PPT)
文档属性
| 名称 | 第五单元: 面积(单元复习课件)-三年级数学下册 人教版(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 15:03:10 | ||
图片预览











文档简介
(共40张PPT)
面 积
复习专题
人教版三年级数学下册
1
面积和面积单位
2
长方形、正方形面积的计算
3
面积单位间的进率
4
解决与长方形、正方形面积有关的实际问题
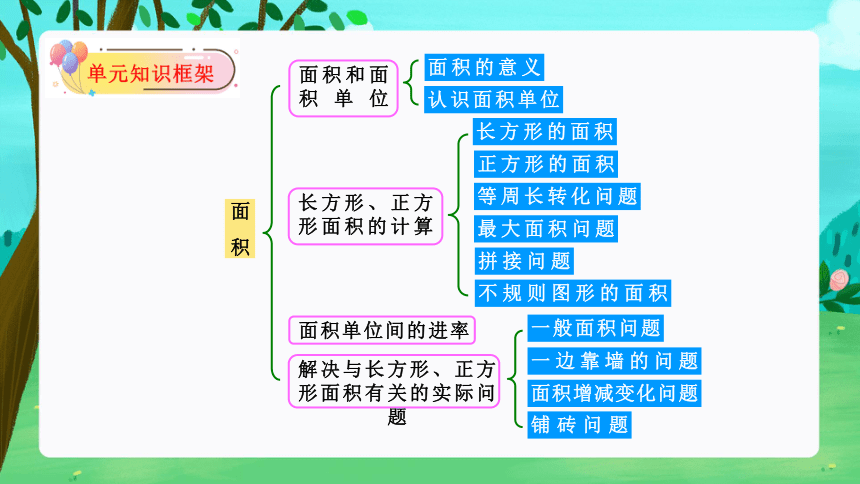
面 积
面积和面积单位
面积的意义
认识面积单位
长方形、正方形面积的计算
长方形的面积
正方形的面积
面积单位间的进率
一般面积问题
一边靠墙的问题
解决与长方形、正方形面积有关的实际问题
不规则图形的面积
等周长转化问题
最大面积问题
拼接问题
面积增减变化问题
铺砖问题
1
面积和面积单位
1、面积的意义
(1)面积:物体表面或封闭图形的大小,叫做它们的面积。
(2)比较两个图形面积的大小,要用统一的面积单位来测量。
2、认识面积单位
(1)常用的面积单位有:平方厘米、平方分米、平方米。
(2)边长是1厘米、1分米、1米的正方形的面积分别是1平方厘米、1平方分米、1平方米。
(3)测量较小物体的面积用平方厘米作单位,测量稍大物体的面积用平方分米作单位,测量较大物体的面积用平方米作单位。
【例1】下面活动中,和“面积”有关的是( )。
A、测量跑道的长度
B、给照片加个边框
C、在墙面上刷一层油漆
选项A测量跑道的长度和选项B给照片加个边框,是和周长有关;
选项C在墙面上刷一层油漆,是和面积有关。
C
面积的意义
【例2】在括号里填上合适的单位名称。
(1)一张报纸的面积大约是24( );
(2)一块黑板的面积大约是4( );
(3)一间房间的占地的面积大约是12( );
(4)一个小学生的身高大约是152( ) ;
(5)一条跑道的长度是50( )。
平方分米
平方米
平方米
厘米
米
认识面积单位
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。( )
根据物体占平面的大小,就是物体的面积。所以桌面的大小就是桌面的面积,原题说法正确。
√
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。 ( )
长度和面积是两种不同意义的量,长度单位和面积单位的意义不同,无法比较大小。原题说法错误。
×
√
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。 ( )
根据生活经验和对面积单位大小的认识可知,一张扑克牌大约40平方厘米。原题说法错误。
×
√
×
2
长方形、正方形面积的计算
1、长方形的面积=长×宽
已知面积求长:长=面积÷宽
已知面积求宽:宽=面积÷长
2、正方形的面积=边长×边长
3、估计物体的面积时,可以借助熟悉的物体的面积作为“非标准”面积单位进行测量,也可以根据已有的知识经验进行估计。
【例4】一个长方形的长是12厘米,宽比长短7厘米,这个长方形的面积是( )平方厘米,周长是( )厘米。
先由长方形的宽=长方形的长-7,计算出长方形的宽:
12-7=5(厘米)
再根据长方形的面积=长×宽,算出面积即可。
12×5=60(平方厘米)
60
长方形的面积
【例4】一个长方形的长是12厘米,宽比长短7厘米,这个长方形的面积是( )平方厘米,周长是( )厘米。
根据长方形的周长=(长+宽)×2,算出周长。
(12+5)×2
=17×2
=34(厘米)
60
34
【例5】一个长方形的面积是63平方厘米,长是9厘米,则这个长方形的周长是( )厘米。
先根据长方形的宽=长方形的面积÷长,求出宽:
63÷9=7(厘米)
再根据长方形的周长=(长+宽)×2,算出周长:
(9+7)×2
=16×2
=32(厘米)
32
正方形的面积
【例6】一个边长是7厘米的正方形,周长是( )厘米,面积是( )平方厘米。
根据正方形的周长=边长×4,求出周长:
7×4=32(厘米);
根据正方形的面积=边长×边长,求出面积:
7×8=49(平方厘米)
28
49
等周长转化问题
【例7】一个长方形的长是12厘米,宽是8厘米。有一个正方形和这根长方形周长相等,正方形的面积是多少平方厘米?
【解析】长方形周长=(长+宽)×2,求出长方形的周长,即正方形的周长;再由正方形边长=正方形周长÷4,求出正方形边长;最后用面积公式:正方形面积=边长×边长,求出正方形面积。
【例7】一个长方形的长是12厘米,宽是8厘米。有一个正方形和这根长方形周长相等,正方形的面积是多少平方厘米?
(12+8)×2
=20×2
=40(厘米)
40÷4=10 (厘米)
10×10=100(平方厘米)
答:正方形的面积是100平方厘米。
最大面积问题
【例8】从一个长20厘米,宽15厘米的长方形中剪下1个面积最大的正方形,剩下部分的面积是( )平方厘米。
以长方形的宽为正方形的边长,可以剪下一个面积最大的正方形。剩下的部分是一个长方形,宽是15厘米,长是20-15=5(厘米);根据长方形的面积=长×宽可得:15×5=75(平方厘米)
75
拼接问题
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
(1)【解析】①当长相接时
大长方形的长是(5+5)厘米,宽是8厘米。
根据长方形的周长=(长+宽)×2,可以求出周长。
②当宽相接时
大长方形的长是8+8=16厘米,宽是5厘米。
根据长方形的周长=(长+宽)×2,可以求出周长。
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
5+5=10厘米
(10+8)×2
=18×2
=36(厘米)
8+8 =16(厘米)
(16+5)×2
=21×2
=42(厘米)
答:大长方形的周长是36厘米或42厘米。
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
(2)【解析】将两个长方形拼成一个大长方形,大长方形的面积等于两个长方形的面积和,根据长方形的面积=长×宽,求出一个长方形的面积,再乘2即可。
8×5×2
=40×2
=80(平方厘米)
答:大长方形的面积是80平方厘米。
【例10】把4个边长是3厘米的小正方形拼成一个长方形,这个长方形的面积是( )平方厘米。
A、12 B、36 C、42
要用4个边长是3厘米的正方形拼成一个长方形,可以4个排成一排,则拼接得到的长方形长为:3×4=12(厘米),宽为3厘米。再根据长方形的面积=长×宽,求出面积为:12×3=36(平方厘米)。
B
【例11】计算下面图形的面积。(单位:厘米)
【解析】把这个图形看成是由一个长4厘米、宽5厘米的长方形和一个长16厘米、宽(11-5)厘米的长方形拼成的,它的面积是:
4×5+16×(11-5)
=20+96
=116(平方厘米)
不规则图形的面积
【例12】下图是将一个边长为7厘米的正方形去掉一部分后剩下的图形,这个图形面积是( )平方厘米。
【解析】这个图形的面积等于正方形的面积减去一个长4厘米、宽2厘米的长方形的面积。
7×7-4×2
=49-8
=41(平方厘米)
41
3
面积单位间的进率
1、面积单位间的进率
每相邻的两个面积单位间的进率都是100,
即1平方米=100平方分米,1平方分米=100平方厘米。
2、面积单位间的换算方法:
【例13】在括号里填上“>”“<”或“=”。
800平方分米( )9平方米;
3000平方分米( )25平方米;
600平方厘米( )6平方分米。
9平方米=900平方分米>800平方分米;
25平方米=2500平方分米<3000平方分米;
6平方分米=600平方厘米。
<
>
=
比较两个图形面积的大小,要先统一的面积单位。
【例14】下列选项中,最接近1平方米的是( )。
A、9平方分米 B、900平方分米 C、9000平方厘米
1平方米=100平方分米
9000平方厘米=90平方分米
9平方分米<90平方分米<100平方分米<900平方分米
所以最接近1平方米的是90平方分米,即9000平方厘米。
C
4
解决问题
【例15】有一个边长为40米的正方形花圃,如果这个花圃每平方米的土地大约可以种3株花,这个花圃大约可种多少株花?
【解析】根据正方形的面积=边长×边长,计算出花圃的面积。再用面积乘以每平方米可种的花的株数,即可得到总数量。
40×40=1600(平方米)
1600×3=4800(株)
答:这个花圃大约可种4800株花。
【例16】做一张名片需要一张长9厘米、宽5厘米的卡纸。做20张这样的名片需要多少平方厘米的卡纸?
【解析】先根据长方形的面积=长×宽计算一张名片所需卡纸的面积;然后将一张名片的面积乘以数量,即可得到所需卡纸的总面积。
9×5=45(平方厘米)
45×20=900(平方厘米)
答:做20张这样的名片需要900平方厘米的卡纸。
【例17】一块长方形草地,长15米,宽9米,草地中有一条小路穿过(如图),小路的宽是2米,这块草地实际面积是多少平方米?
【解析】先计算出长方形草地原来的面积,再减去小路所占的面积,即可得到草地实际的面积。
15×9=135(平方米)
2×15=30(平方米)
135-30=105(平方米)
答:这块草地实际面积是105平方米。
一边靠墙的问题
【例18】给一块一边靠墙的正方形空地(如图)的其它几条边围上篱笆,篱笆长48米。这块空地的面积是多少平方米?
【解析】因为正方形空地一边靠墙,所以篱笆只需要围三面,也就是正方形三条边的长度之和为48米。根据篱笆长度÷3=正方形边长,边长×边长=正方形空地面积,列式计算即可。
48÷3=16(米)
16×16=256(平方米)
答:这块空地的面积是256平方米。
面积增减变化问题
【例19】一个长方形花坛,长为15米,面积是135平方米。若将这个花坛的长增加到30米,宽不变,则扩大后的花坛的面积是多少平方米?
【解析】先根据长方形的宽=长方形的面积÷长,求出原来长方形的宽;再根据扩大后的长×原来的宽=扩大后的长方形面积,列式计算即可。
135÷15=9(米)
30×9=270(平方米)
答:扩大后的花坛的面积是270平方米。
【例20】一个长方形,如果长减少3米,面积就减少18平方米;如果宽增加2米,面积就增加16平方米。这个长方形原来的面积是多少平方米?
【解析】①减少的部分是一个长方形,长是原来长方形的宽,长是3米,用减少部分的面积除以减少的长度,即可算出原来长方形的宽是(18÷3)米。
②增加的部分是一个长方形,长是原来长方形的长,宽是2米。用增加部分的面积除以增加的长度,即可算出原来长方形的长是(16÷2)米。
③根据长方形面积=长×宽,求出长方形原来的面积。
【例20】一个长方形,如果长减少3米,面积就减少18平方米;如果宽增加2米,面积就增加16平方米。这个长方形原来的面积是多少平方米?
18÷3=6(米)
16÷2=9(米)
6×9=54(平方米)
答:这个长方形原来的面积是54平方米。
【例21】将一个正方形水池的边长增加2米,则水池的面积增加36平方米,求原来正方形水池的面积是多少平方米?
【解析】边长增加2米,增加的面积可以分成3部分:图形①和图形②都是长为原来正方形的边长,宽是2米的长方形;图形③是边长是2米的正方形。
从增加的面积36平方米中减去小正方形的面积,得到两个长方形的面积,再除以2可以其中一个长方形的面积;进而求得原正方形的边长;然后求出正方形面积即可。
【例21】将一个正方形水池的边长增加2米,则水池的面积增加36平方米,求原来正方形水池的面积是多少平方米?
2×2=4(平方米)
36-4=32(平方米)
32÷2÷2
=16÷2
=8(米)
8×8=64(平方米)
答:这个长方形原来的面积是64平方米。
铺砖问题
【例22】有一间边长为6米的正方形会议室,用面积是4平方分米的方砖来铺这间会议室,一共需要多少块方砖?
【解析】先根据正方形的面积=边长×边长求出正方形会议室的面积,再会议室的面积除以每块方砖的面积,就可得到所需方砖的块数。
6×6=36(平方米)
36平方米=3600(平方分米)
3600÷4=900(块)
答:一共需要900块方砖。
1、一个正方形的边长是7分米,周长是( )分米,面积是( )平方分米。
2、要给一张长方形饭桌的桌面配一块玻璃,使它刚好盖住桌面,在玻璃四周包上防撞条。已知这张饭桌的桌面长12分米,宽6分米。那么玻璃的面积是( )平方厘米,防撞条长( )厘米。
28
49
72
36
3、有一个周长是52厘米的正方形,它的面积是( )平方厘米。
A.121 B.144 C.169 D.196
4、有一块长3米,宽2米的长方形墙面,要求用整块的正方形瓷砖正好贴满,能用边长是( )厘米规格的正方形瓷砖。
A.4 B.6 C.8 D.10
C
D
5、一个长方形菜园长是15米,宽是8米。这个菜园的面积是多少平方米?如果每平方米大约种20棵白菜,这个菜园可以种多少棵白菜?
15×8=120(平方米)
20×120=2400(棵)
答:这个菜园的面积是120平方米,可以种2400棵白菜。
每一份努力,都将在学习中得到最好的回报。加油!
面 积
复习专题
人教版三年级数学下册
1
面积和面积单位
2
长方形、正方形面积的计算
3
面积单位间的进率
4
解决与长方形、正方形面积有关的实际问题
面 积
面积和面积单位
面积的意义
认识面积单位
长方形、正方形面积的计算
长方形的面积
正方形的面积
面积单位间的进率
一般面积问题
一边靠墙的问题
解决与长方形、正方形面积有关的实际问题
不规则图形的面积
等周长转化问题
最大面积问题
拼接问题
面积增减变化问题
铺砖问题
1
面积和面积单位
1、面积的意义
(1)面积:物体表面或封闭图形的大小,叫做它们的面积。
(2)比较两个图形面积的大小,要用统一的面积单位来测量。
2、认识面积单位
(1)常用的面积单位有:平方厘米、平方分米、平方米。
(2)边长是1厘米、1分米、1米的正方形的面积分别是1平方厘米、1平方分米、1平方米。
(3)测量较小物体的面积用平方厘米作单位,测量稍大物体的面积用平方分米作单位,测量较大物体的面积用平方米作单位。
【例1】下面活动中,和“面积”有关的是( )。
A、测量跑道的长度
B、给照片加个边框
C、在墙面上刷一层油漆
选项A测量跑道的长度和选项B给照片加个边框,是和周长有关;
选项C在墙面上刷一层油漆,是和面积有关。
C
面积的意义
【例2】在括号里填上合适的单位名称。
(1)一张报纸的面积大约是24( );
(2)一块黑板的面积大约是4( );
(3)一间房间的占地的面积大约是12( );
(4)一个小学生的身高大约是152( ) ;
(5)一条跑道的长度是50( )。
平方分米
平方米
平方米
厘米
米
认识面积单位
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。( )
根据物体占平面的大小,就是物体的面积。所以桌面的大小就是桌面的面积,原题说法正确。
√
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。 ( )
长度和面积是两种不同意义的量,长度单位和面积单位的意义不同,无法比较大小。原题说法错误。
×
√
【例3】判断题。(对的画“√“,错的画“×”)
(1)桌面的大小就是桌面的面积。( )
(2)长度单位比面积单位大。( )
(3)一张扑克牌大约40平方分米。 ( )
根据生活经验和对面积单位大小的认识可知,一张扑克牌大约40平方厘米。原题说法错误。
×
√
×
2
长方形、正方形面积的计算
1、长方形的面积=长×宽
已知面积求长:长=面积÷宽
已知面积求宽:宽=面积÷长
2、正方形的面积=边长×边长
3、估计物体的面积时,可以借助熟悉的物体的面积作为“非标准”面积单位进行测量,也可以根据已有的知识经验进行估计。
【例4】一个长方形的长是12厘米,宽比长短7厘米,这个长方形的面积是( )平方厘米,周长是( )厘米。
先由长方形的宽=长方形的长-7,计算出长方形的宽:
12-7=5(厘米)
再根据长方形的面积=长×宽,算出面积即可。
12×5=60(平方厘米)
60
长方形的面积
【例4】一个长方形的长是12厘米,宽比长短7厘米,这个长方形的面积是( )平方厘米,周长是( )厘米。
根据长方形的周长=(长+宽)×2,算出周长。
(12+5)×2
=17×2
=34(厘米)
60
34
【例5】一个长方形的面积是63平方厘米,长是9厘米,则这个长方形的周长是( )厘米。
先根据长方形的宽=长方形的面积÷长,求出宽:
63÷9=7(厘米)
再根据长方形的周长=(长+宽)×2,算出周长:
(9+7)×2
=16×2
=32(厘米)
32
正方形的面积
【例6】一个边长是7厘米的正方形,周长是( )厘米,面积是( )平方厘米。
根据正方形的周长=边长×4,求出周长:
7×4=32(厘米);
根据正方形的面积=边长×边长,求出面积:
7×8=49(平方厘米)
28
49
等周长转化问题
【例7】一个长方形的长是12厘米,宽是8厘米。有一个正方形和这根长方形周长相等,正方形的面积是多少平方厘米?
【解析】长方形周长=(长+宽)×2,求出长方形的周长,即正方形的周长;再由正方形边长=正方形周长÷4,求出正方形边长;最后用面积公式:正方形面积=边长×边长,求出正方形面积。
【例7】一个长方形的长是12厘米,宽是8厘米。有一个正方形和这根长方形周长相等,正方形的面积是多少平方厘米?
(12+8)×2
=20×2
=40(厘米)
40÷4=10 (厘米)
10×10=100(平方厘米)
答:正方形的面积是100平方厘米。
最大面积问题
【例8】从一个长20厘米,宽15厘米的长方形中剪下1个面积最大的正方形,剩下部分的面积是( )平方厘米。
以长方形的宽为正方形的边长,可以剪下一个面积最大的正方形。剩下的部分是一个长方形,宽是15厘米,长是20-15=5(厘米);根据长方形的面积=长×宽可得:15×5=75(平方厘米)
75
拼接问题
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
(1)【解析】①当长相接时
大长方形的长是(5+5)厘米,宽是8厘米。
根据长方形的周长=(长+宽)×2,可以求出周长。
②当宽相接时
大长方形的长是8+8=16厘米,宽是5厘米。
根据长方形的周长=(长+宽)×2,可以求出周长。
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
5+5=10厘米
(10+8)×2
=18×2
=36(厘米)
8+8 =16(厘米)
(16+5)×2
=21×2
=42(厘米)
答:大长方形的周长是36厘米或42厘米。
【例9】用2个长8厘米,宽5厘米的小长方形拼成一个大长方形,大长方形的周长是多少厘米?面积是多少平方厘米?
(2)【解析】将两个长方形拼成一个大长方形,大长方形的面积等于两个长方形的面积和,根据长方形的面积=长×宽,求出一个长方形的面积,再乘2即可。
8×5×2
=40×2
=80(平方厘米)
答:大长方形的面积是80平方厘米。
【例10】把4个边长是3厘米的小正方形拼成一个长方形,这个长方形的面积是( )平方厘米。
A、12 B、36 C、42
要用4个边长是3厘米的正方形拼成一个长方形,可以4个排成一排,则拼接得到的长方形长为:3×4=12(厘米),宽为3厘米。再根据长方形的面积=长×宽,求出面积为:12×3=36(平方厘米)。
B
【例11】计算下面图形的面积。(单位:厘米)
【解析】把这个图形看成是由一个长4厘米、宽5厘米的长方形和一个长16厘米、宽(11-5)厘米的长方形拼成的,它的面积是:
4×5+16×(11-5)
=20+96
=116(平方厘米)
不规则图形的面积
【例12】下图是将一个边长为7厘米的正方形去掉一部分后剩下的图形,这个图形面积是( )平方厘米。
【解析】这个图形的面积等于正方形的面积减去一个长4厘米、宽2厘米的长方形的面积。
7×7-4×2
=49-8
=41(平方厘米)
41
3
面积单位间的进率
1、面积单位间的进率
每相邻的两个面积单位间的进率都是100,
即1平方米=100平方分米,1平方分米=100平方厘米。
2、面积单位间的换算方法:
【例13】在括号里填上“>”“<”或“=”。
800平方分米( )9平方米;
3000平方分米( )25平方米;
600平方厘米( )6平方分米。
9平方米=900平方分米>800平方分米;
25平方米=2500平方分米<3000平方分米;
6平方分米=600平方厘米。
<
>
=
比较两个图形面积的大小,要先统一的面积单位。
【例14】下列选项中,最接近1平方米的是( )。
A、9平方分米 B、900平方分米 C、9000平方厘米
1平方米=100平方分米
9000平方厘米=90平方分米
9平方分米<90平方分米<100平方分米<900平方分米
所以最接近1平方米的是90平方分米,即9000平方厘米。
C
4
解决问题
【例15】有一个边长为40米的正方形花圃,如果这个花圃每平方米的土地大约可以种3株花,这个花圃大约可种多少株花?
【解析】根据正方形的面积=边长×边长,计算出花圃的面积。再用面积乘以每平方米可种的花的株数,即可得到总数量。
40×40=1600(平方米)
1600×3=4800(株)
答:这个花圃大约可种4800株花。
【例16】做一张名片需要一张长9厘米、宽5厘米的卡纸。做20张这样的名片需要多少平方厘米的卡纸?
【解析】先根据长方形的面积=长×宽计算一张名片所需卡纸的面积;然后将一张名片的面积乘以数量,即可得到所需卡纸的总面积。
9×5=45(平方厘米)
45×20=900(平方厘米)
答:做20张这样的名片需要900平方厘米的卡纸。
【例17】一块长方形草地,长15米,宽9米,草地中有一条小路穿过(如图),小路的宽是2米,这块草地实际面积是多少平方米?
【解析】先计算出长方形草地原来的面积,再减去小路所占的面积,即可得到草地实际的面积。
15×9=135(平方米)
2×15=30(平方米)
135-30=105(平方米)
答:这块草地实际面积是105平方米。
一边靠墙的问题
【例18】给一块一边靠墙的正方形空地(如图)的其它几条边围上篱笆,篱笆长48米。这块空地的面积是多少平方米?
【解析】因为正方形空地一边靠墙,所以篱笆只需要围三面,也就是正方形三条边的长度之和为48米。根据篱笆长度÷3=正方形边长,边长×边长=正方形空地面积,列式计算即可。
48÷3=16(米)
16×16=256(平方米)
答:这块空地的面积是256平方米。
面积增减变化问题
【例19】一个长方形花坛,长为15米,面积是135平方米。若将这个花坛的长增加到30米,宽不变,则扩大后的花坛的面积是多少平方米?
【解析】先根据长方形的宽=长方形的面积÷长,求出原来长方形的宽;再根据扩大后的长×原来的宽=扩大后的长方形面积,列式计算即可。
135÷15=9(米)
30×9=270(平方米)
答:扩大后的花坛的面积是270平方米。
【例20】一个长方形,如果长减少3米,面积就减少18平方米;如果宽增加2米,面积就增加16平方米。这个长方形原来的面积是多少平方米?
【解析】①减少的部分是一个长方形,长是原来长方形的宽,长是3米,用减少部分的面积除以减少的长度,即可算出原来长方形的宽是(18÷3)米。
②增加的部分是一个长方形,长是原来长方形的长,宽是2米。用增加部分的面积除以增加的长度,即可算出原来长方形的长是(16÷2)米。
③根据长方形面积=长×宽,求出长方形原来的面积。
【例20】一个长方形,如果长减少3米,面积就减少18平方米;如果宽增加2米,面积就增加16平方米。这个长方形原来的面积是多少平方米?
18÷3=6(米)
16÷2=9(米)
6×9=54(平方米)
答:这个长方形原来的面积是54平方米。
【例21】将一个正方形水池的边长增加2米,则水池的面积增加36平方米,求原来正方形水池的面积是多少平方米?
【解析】边长增加2米,增加的面积可以分成3部分:图形①和图形②都是长为原来正方形的边长,宽是2米的长方形;图形③是边长是2米的正方形。
从增加的面积36平方米中减去小正方形的面积,得到两个长方形的面积,再除以2可以其中一个长方形的面积;进而求得原正方形的边长;然后求出正方形面积即可。
【例21】将一个正方形水池的边长增加2米,则水池的面积增加36平方米,求原来正方形水池的面积是多少平方米?
2×2=4(平方米)
36-4=32(平方米)
32÷2÷2
=16÷2
=8(米)
8×8=64(平方米)
答:这个长方形原来的面积是64平方米。
铺砖问题
【例22】有一间边长为6米的正方形会议室,用面积是4平方分米的方砖来铺这间会议室,一共需要多少块方砖?
【解析】先根据正方形的面积=边长×边长求出正方形会议室的面积,再会议室的面积除以每块方砖的面积,就可得到所需方砖的块数。
6×6=36(平方米)
36平方米=3600(平方分米)
3600÷4=900(块)
答:一共需要900块方砖。
1、一个正方形的边长是7分米,周长是( )分米,面积是( )平方分米。
2、要给一张长方形饭桌的桌面配一块玻璃,使它刚好盖住桌面,在玻璃四周包上防撞条。已知这张饭桌的桌面长12分米,宽6分米。那么玻璃的面积是( )平方厘米,防撞条长( )厘米。
28
49
72
36
3、有一个周长是52厘米的正方形,它的面积是( )平方厘米。
A.121 B.144 C.169 D.196
4、有一块长3米,宽2米的长方形墙面,要求用整块的正方形瓷砖正好贴满,能用边长是( )厘米规格的正方形瓷砖。
A.4 B.6 C.8 D.10
C
D
5、一个长方形菜园长是15米,宽是8米。这个菜园的面积是多少平方米?如果每平方米大约种20棵白菜,这个菜园可以种多少棵白菜?
15×8=120(平方米)
20×120=2400(棵)
答:这个菜园的面积是120平方米,可以种2400棵白菜。
每一份努力,都将在学习中得到最好的回报。加油!
