河北省承德市兴隆县2023-2024学年九年级下学期期中数学试题(含答案)
文档属性
| 名称 | 河北省承德市兴隆县2023-2024学年九年级下学期期中数学试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览




文档简介
2024年初中毕业升学文化课模拟考试
数学试卷(一)
卷I(选择题共38分)
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1.计算得,则“?”是( )
A.0 B.1 C.2 D.3
2.如图,将折叠,使点落在边处,展开后得到折痕,则是的( )
A.高线 B.角平分线 C.中线 D.中位线
3.射线的速度为光速的十分之一,若光速为m/s,则射线的速度用科学记数法可表示为( )
A.m/s B.m/s C.m/s D.m/s
4.如图所示的几何体由9个大小相同的小正方体组成,将小正方体1去掉后,所得几何体的三视图没有发生变化的是( )
A.主视图和左视图 B.主视图和俯视图 C.左视图和俯视图 D.主视图、左视图、俯视图
5.若,则代数式的值为( )
A. B. C.2 D.
6.有一个摊位游戏,先旋转一个转盘的指针,如果指针箭头停在奇数的位置,玩的人可以从袋子里抽出一个弹珠,当摸到黑色的弹珠就能得到奖品,转盘和弹珠如下图所示,小明玩了一次这个游戏,则小明得奖的可能性为( )
A.不可能 B.不太可能 C.非常有可能
7.若使用如图所示的,两根直铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以分为两段的铁丝是( )
A.,都可以 B.,都不可以 C.只有可以 D.只有可以
8.已知,,用含、的代数式表示,这个代数式是( )
A. B. C. D.
9.依据所标数据,下列图形中一定为平行四边形的是( )
A. B. C. D.
10.在中,要判断和的大小关系(和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
方案Ⅰ: ①以点为圆心,长为半径作; ②观察点与的位置关系即可。 方案Ⅱ: ①作边的垂直平分线; ②观察与边是否有交点位置关系即可。
对于方案Ⅰ、Ⅱ说法正确的是( )
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行 C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
11.如图,小明为了测量一凉亭的高度(顶端到水平地面的距离),在凉亭的旁边放置一个与凉亭台阶等高的台阶(m,,,三点共线),把一面镜子水平放置在平台上的点处,测得m,然后沿直线后退到点处,这时恰好在镜子里看到凉亭的顶端,测得m,小明身高m,则凉亭的高度约为( )
A.8.5m B.9m C.9.5m D.10m
12.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形的中心重合,且与边、相交于、(如图).图中阴影部分的面积记为,三条线段、、的长度之和记为,在大正六边形绕点旋转过程中,下列说法正确的是( )
A.变化,不变 B.不变,变化 C.变化,变化 D.与均不变
13.将一副直角三角板作如图所示摆放,,,,则下列结论不正确的是( )
A. B. C. D.
14.某女子排球队6名场上队员的身高(单位:cm)是:172,174,178,180,180,184.现用身高为177cm的队员替换场上身高为174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,中位数不变 B.平均数变小,中位数变大
C.平均数变大,中位数不变 D.平均数变大,中位数变大
15.如图,是半圆的直径,、、三点依次在半圆上,若,,则与之间的关系是( )
A. B. C. D.
16.如图是一种轨道示意图,其中、、、分别是正方形的四个顶点,现有两个机器人(看成点)分别从,两点同时出发,沿着轨道以相同的速度匀速移动,其路线分别为和.若移动时间为,两个机器人之间距离为.则与之间的函数关系用图象表示大致为( )
A. B. C. D.
Ⅱ(非选择题,共82分)
二、填空题(本大题共3个小题,每空2分,共10分.)
17.已知,,则__________.
18.如图,等腰中,,,是边上的点,将沿翻折得到,边交于点.
(1)___________°;
(2)若,则__________°.
19.如图,已知点,,点在线段上,并且点的横、纵坐标均为整数.经过点的双曲线为.
(1)当点与点重合时,的值为___________;
(2)的最大值为__________.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)
已知、是两个整式,,.
(1)尝试计算
当时,_____________________
当时,_____________________
(2)大胆猜想
小军猜测:无论为何值,__________始终成立(填“>”、=或“<”).
(3)小心验证
请证明小军猜测的结论.
21.(本小题满分9分)
在知识竞赛中,规定答对一题加5分,答错一题(不答按答错)扣3分,
小明答对道题,答错道题.
(1)用含,的式子表示小明的得分为__________分;
(2)若小明答对20道题,总分在80分以上,求他最多答错多少道题.
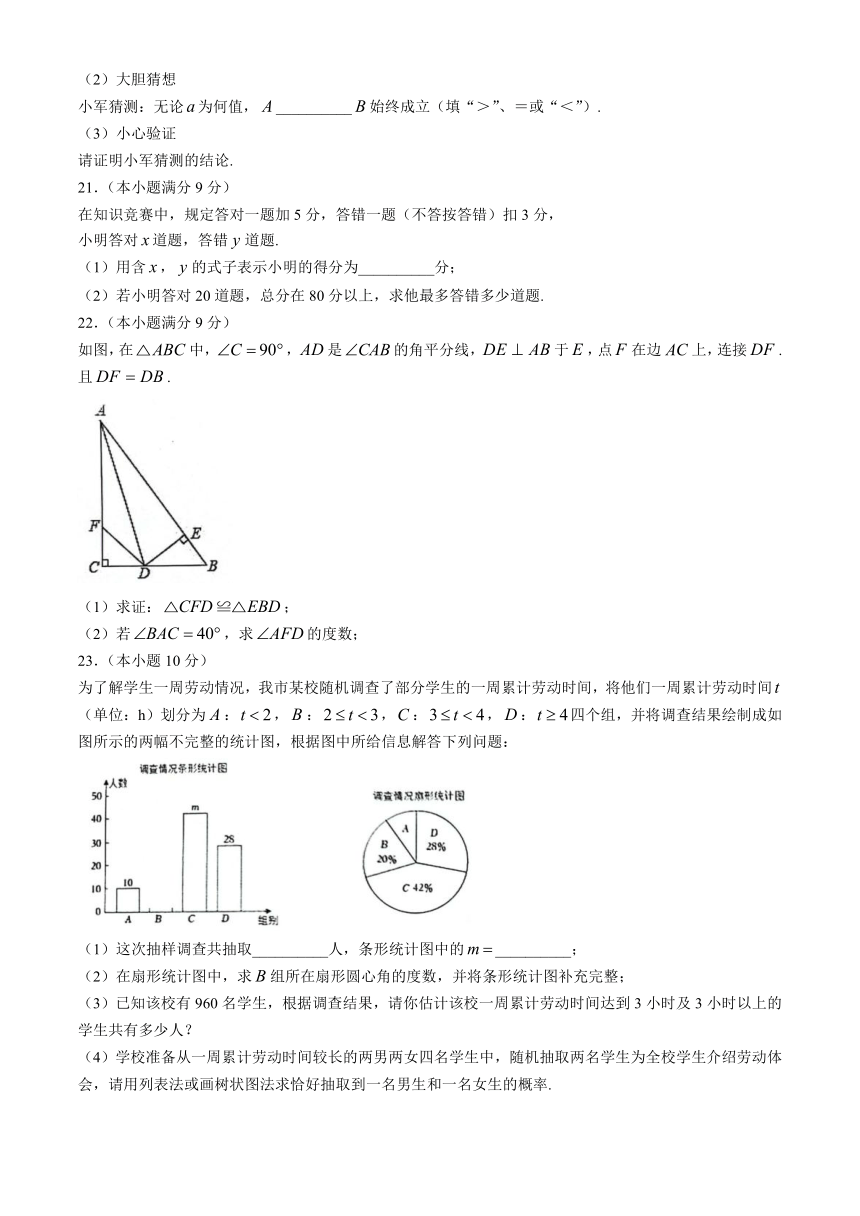
22.(本小题满分9分)
如图,在中,,是的角平分线,于,点在边上,连接.且.
(1)求证:;
(2)若,求的度数;
23.(本小题10分)
为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间(单位:h)划分为:,:,:,:四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取__________人,条形统计图中的__________;
(2)在扇形统计图中,求组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
24.(本小题10分)
已知:,
(1)求的解析式;
(2)直线与线段有公共点,求的取值范围.
(3)点为线段上的点,若直线把的面积分成1:2两部分,直接写出点的坐标.
25.(本小题12分)
高楼火灾越来越受到重视,某区消防中队开展消防技能比赛,如图,在一废弃高楼距地面10m的点和其正上方点处各设置了一个火源.消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与距离忽略不计),第一次灭火时,站在水平地面上的点处,水流恰好到达点处,且水流的最大高度为12m,待处火熄灭后,消防员退到点处,调整水枪进行第二次灭火,使水流恰好到达点处,已知点到高楼的水平距离为12m,假设两次灭火时水流的最高点的水平距离均为3m,建立如图所示的平面直角坐标系,水流的高度(m)与到高楼的水平距离(m)之间的函数关系式为.
(1)求消防员第一次灭火时水流所在抛物线的解析式;
(2)若两次灭火时水流所在抛物线的形状相同,求,之间的距离;
(3)若消防员站在到高楼水平距离为9m的地方,想要扑灭距地面高度12~8m范围内的火苗,当水流最高点到高楼的水平距离始终为3m时,求的取值范围.
26.(本小题13分)
如图,在中,,,,点是的中点.动点沿边从点开始,向点以每秒1个单位长度的速度运动,当点到达点时停止运动,以点为圆心,的长为半径作圆,与交于点,过点作,垂足为点.设运动的时间为秒.
(1)___________,____________;
(2)求的长(用含的代数式表示);
(3)当与相切时,切点为,求的长(,结果保留);
(4)当与线段有交点时,直接写出的取值范围和线段所扫过的面积.
兴隆县2023-2024学年第二学期九年级数学
模拟试卷答案(一)
卷Ⅰ(选择题共38分)
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
D A A A D B C D C C C D C C A B
Ⅱ(非选择题,共82分)
二、填空题(本大题共3个小题,每空2分,共10分.)
17.24 18. 72.5°、107.5° 19. 7 10
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20、(本小题满分9分)
解:(1)每空1分,计4分.
故答案为:2,,8,;
(2)小军猜测:无论为何值,始终成立. 6分
(3)
无论为何值, 9分
21.(本小题满分9分)
【详解】(1)由题意得:; 3分
由题意得: 6分
.小明最多答错6道题 9分
22.(本小题满分9分)
(1)证明:是的角平分线,,
,
; 5分
(2),, 6分
, 8分
9分
23.(本小题10分)
解:(1)这次抽样调查的总人数为(人),
所以;
故答案为:100;42;.........................2分
(2)组所在扇形圆心角的度数为; 3分
组人数为(人),
条形统计图补充完整为:
4分
(3)(人),
所以估计该校一周累计芳动时间达到3小时及3小时以上的学生共有672人; 6分
(4)画树状图为:
8分
共有12种等可能的结果,其中一名男生和一名女生的结果数为8,
所以恰好抽取到一名男生和一名女生的概率 10分
24.(本小题10分)
解:(1)设直线的解析式为
根据题意得解得,
所以的解析式为: 4分
(2)直线过点得,直线过点得
8分
(3)或 10分
25.(本小题12分)
(1)解:由题意可知第一次灭火时水流最高点的坐标为,
设水流所在抛物线的解析式为,点在抛物线上,
,解得,,
消防员第一次灭火时水流所在抛物线解析式为; 4分
(2)两次灭火时水流所在抛物线的形状相同,且水流的最高点到高楼的水平距离均为3米,可设第二次灭火时水流所在抛物线的解析式为
由题意可知该抛物线过点,,解, 6分
,令,则,
,,
,即4、之间的距离为6m; 8分
(3)解:由题意可知灭火过程中与始终满足,将代入后可得,,
, 10分
当抛物线过点时,,解得;
当抛物线过点时,,解得;
; 12分
26.(本小题13分)
解:(1), 2分
(2)由题意得,,
,
在中,,
在中,; 5分
(3)如图所示,设与相切于,连接,
,
在中,,,,
,
,
,
, 7分
,,, 8分
弧的长 10分
(3)如图所示,当恰好经过点时,连接,
,,点为的中点,
,
,
,,
;
如图所示,当恰好经过点时,
,
,
,,
,
,
与线段有交点,
线段所扫过的面积即为梯形的面积,
线段所扫过的面积.
所以答案为 12分
面积为0.3. 13分
数学试卷(一)
卷I(选择题共38分)
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1.计算得,则“?”是( )
A.0 B.1 C.2 D.3
2.如图,将折叠,使点落在边处,展开后得到折痕,则是的( )
A.高线 B.角平分线 C.中线 D.中位线
3.射线的速度为光速的十分之一,若光速为m/s,则射线的速度用科学记数法可表示为( )
A.m/s B.m/s C.m/s D.m/s
4.如图所示的几何体由9个大小相同的小正方体组成,将小正方体1去掉后,所得几何体的三视图没有发生变化的是( )
A.主视图和左视图 B.主视图和俯视图 C.左视图和俯视图 D.主视图、左视图、俯视图
5.若,则代数式的值为( )
A. B. C.2 D.
6.有一个摊位游戏,先旋转一个转盘的指针,如果指针箭头停在奇数的位置,玩的人可以从袋子里抽出一个弹珠,当摸到黑色的弹珠就能得到奖品,转盘和弹珠如下图所示,小明玩了一次这个游戏,则小明得奖的可能性为( )
A.不可能 B.不太可能 C.非常有可能
7.若使用如图所示的,两根直铁丝做成一个三角形框架,需要将其中一根铁丝折成两段,则可以分为两段的铁丝是( )
A.,都可以 B.,都不可以 C.只有可以 D.只有可以
8.已知,,用含、的代数式表示,这个代数式是( )
A. B. C. D.
9.依据所标数据,下列图形中一定为平行四边形的是( )
A. B. C. D.
10.在中,要判断和的大小关系(和均为锐角),同学们提供了许多方案,老师选取其中两位同学的方案(如图1和图2)
方案Ⅰ: ①以点为圆心,长为半径作; ②观察点与的位置关系即可。 方案Ⅱ: ①作边的垂直平分线; ②观察与边是否有交点位置关系即可。
对于方案Ⅰ、Ⅱ说法正确的是( )
A.Ⅰ可行、Ⅱ不可行 B.Ⅰ不可行、Ⅱ可行 C.Ⅰ、Ⅱ都可行 D.Ⅰ、Ⅱ都不可行
11.如图,小明为了测量一凉亭的高度(顶端到水平地面的距离),在凉亭的旁边放置一个与凉亭台阶等高的台阶(m,,,三点共线),把一面镜子水平放置在平台上的点处,测得m,然后沿直线后退到点处,这时恰好在镜子里看到凉亭的顶端,测得m,小明身高m,则凉亭的高度约为( )
A.8.5m B.9m C.9.5m D.10m
12.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形的中心重合,且与边、相交于、(如图).图中阴影部分的面积记为,三条线段、、的长度之和记为,在大正六边形绕点旋转过程中,下列说法正确的是( )
A.变化,不变 B.不变,变化 C.变化,变化 D.与均不变
13.将一副直角三角板作如图所示摆放,,,,则下列结论不正确的是( )
A. B. C. D.
14.某女子排球队6名场上队员的身高(单位:cm)是:172,174,178,180,180,184.现用身高为177cm的队员替换场上身高为174cm的队员,与换人前相比,场上队员的身高( )
A.平均数变小,中位数不变 B.平均数变小,中位数变大
C.平均数变大,中位数不变 D.平均数变大,中位数变大
15.如图,是半圆的直径,、、三点依次在半圆上,若,,则与之间的关系是( )
A. B. C. D.
16.如图是一种轨道示意图,其中、、、分别是正方形的四个顶点,现有两个机器人(看成点)分别从,两点同时出发,沿着轨道以相同的速度匀速移动,其路线分别为和.若移动时间为,两个机器人之间距离为.则与之间的函数关系用图象表示大致为( )
A. B. C. D.
Ⅱ(非选择题,共82分)
二、填空题(本大题共3个小题,每空2分,共10分.)
17.已知,,则__________.
18.如图,等腰中,,,是边上的点,将沿翻折得到,边交于点.
(1)___________°;
(2)若,则__________°.
19.如图,已知点,,点在线段上,并且点的横、纵坐标均为整数.经过点的双曲线为.
(1)当点与点重合时,的值为___________;
(2)的最大值为__________.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)
已知、是两个整式,,.
(1)尝试计算
当时,_____________________
当时,_____________________
(2)大胆猜想
小军猜测:无论为何值,__________始终成立(填“>”、=或“<”).
(3)小心验证
请证明小军猜测的结论.
21.(本小题满分9分)
在知识竞赛中,规定答对一题加5分,答错一题(不答按答错)扣3分,
小明答对道题,答错道题.
(1)用含,的式子表示小明的得分为__________分;
(2)若小明答对20道题,总分在80分以上,求他最多答错多少道题.
22.(本小题满分9分)
如图,在中,,是的角平分线,于,点在边上,连接.且.
(1)求证:;
(2)若,求的度数;
23.(本小题10分)
为了解学生一周劳动情况,我市某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间(单位:h)划分为:,:,:,:四个组,并将调查结果绘制成如图所示的两幅不完整的统计图,根据图中所给信息解答下列问题:
(1)这次抽样调查共抽取__________人,条形统计图中的__________;
(2)在扇形统计图中,求组所在扇形圆心角的度数,并将条形统计图补充完整;
(3)已知该校有960名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人?
(4)学校准备从一周累计劳动时间较长的两男两女四名学生中,随机抽取两名学生为全校学生介绍劳动体会,请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率.
24.(本小题10分)
已知:,
(1)求的解析式;
(2)直线与线段有公共点,求的取值范围.
(3)点为线段上的点,若直线把的面积分成1:2两部分,直接写出点的坐标.
25.(本小题12分)
高楼火灾越来越受到重视,某区消防中队开展消防技能比赛,如图,在一废弃高楼距地面10m的点和其正上方点处各设置了一个火源.消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与距离忽略不计),第一次灭火时,站在水平地面上的点处,水流恰好到达点处,且水流的最大高度为12m,待处火熄灭后,消防员退到点处,调整水枪进行第二次灭火,使水流恰好到达点处,已知点到高楼的水平距离为12m,假设两次灭火时水流的最高点的水平距离均为3m,建立如图所示的平面直角坐标系,水流的高度(m)与到高楼的水平距离(m)之间的函数关系式为.
(1)求消防员第一次灭火时水流所在抛物线的解析式;
(2)若两次灭火时水流所在抛物线的形状相同,求,之间的距离;
(3)若消防员站在到高楼水平距离为9m的地方,想要扑灭距地面高度12~8m范围内的火苗,当水流最高点到高楼的水平距离始终为3m时,求的取值范围.
26.(本小题13分)
如图,在中,,,,点是的中点.动点沿边从点开始,向点以每秒1个单位长度的速度运动,当点到达点时停止运动,以点为圆心,的长为半径作圆,与交于点,过点作,垂足为点.设运动的时间为秒.
(1)___________,____________;
(2)求的长(用含的代数式表示);
(3)当与相切时,切点为,求的长(,结果保留);
(4)当与线段有交点时,直接写出的取值范围和线段所扫过的面积.
兴隆县2023-2024学年第二学期九年级数学
模拟试卷答案(一)
卷Ⅰ(选择题共38分)
一、选择题(本大题共16个小题,1-6每小题3分,7-16每小题2分,共38分.在每个小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
D A A A D B C D C C C D C C A B
Ⅱ(非选择题,共82分)
二、填空题(本大题共3个小题,每空2分,共10分.)
17.24 18. 72.5°、107.5° 19. 7 10
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
20、(本小题满分9分)
解:(1)每空1分,计4分.
故答案为:2,,8,;
(2)小军猜测:无论为何值,始终成立. 6分
(3)
无论为何值, 9分
21.(本小题满分9分)
【详解】(1)由题意得:; 3分
由题意得: 6分
.小明最多答错6道题 9分
22.(本小题满分9分)
(1)证明:是的角平分线,,
,
; 5分
(2),, 6分
, 8分
9分
23.(本小题10分)
解:(1)这次抽样调查的总人数为(人),
所以;
故答案为:100;42;.........................2分
(2)组所在扇形圆心角的度数为; 3分
组人数为(人),
条形统计图补充完整为:
4分
(3)(人),
所以估计该校一周累计芳动时间达到3小时及3小时以上的学生共有672人; 6分
(4)画树状图为:
8分
共有12种等可能的结果,其中一名男生和一名女生的结果数为8,
所以恰好抽取到一名男生和一名女生的概率 10分
24.(本小题10分)
解:(1)设直线的解析式为
根据题意得解得,
所以的解析式为: 4分
(2)直线过点得,直线过点得
8分
(3)或 10分
25.(本小题12分)
(1)解:由题意可知第一次灭火时水流最高点的坐标为,
设水流所在抛物线的解析式为,点在抛物线上,
,解得,,
消防员第一次灭火时水流所在抛物线解析式为; 4分
(2)两次灭火时水流所在抛物线的形状相同,且水流的最高点到高楼的水平距离均为3米,可设第二次灭火时水流所在抛物线的解析式为
由题意可知该抛物线过点,,解, 6分
,令,则,
,,
,即4、之间的距离为6m; 8分
(3)解:由题意可知灭火过程中与始终满足,将代入后可得,,
, 10分
当抛物线过点时,,解得;
当抛物线过点时,,解得;
; 12分
26.(本小题13分)
解:(1), 2分
(2)由题意得,,
,
在中,,
在中,; 5分
(3)如图所示,设与相切于,连接,
,
在中,,,,
,
,
,
, 7分
,,, 8分
弧的长 10分
(3)如图所示,当恰好经过点时,连接,
,,点为的中点,
,
,
,,
;
如图所示,当恰好经过点时,
,
,
,,
,
,
与线段有交点,
线段所扫过的面积即为梯形的面积,
线段所扫过的面积.
所以答案为 12分
面积为0.3. 13分
同课章节目录
