2024年河南省驻马店市新蔡县中考一模考试数学 讲评课件 (共71张PPT)
文档属性
| 名称 | 2024年河南省驻马店市新蔡县中考一模考试数学 讲评课件 (共71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 20:44:09 | ||
图片预览










文档简介
(共71张PPT)
2024年河南省中考模拟试卷
数学
主讲人:某某某老师
某某学校
一、选择题
二、填空题
三、解答题
一、选择题
二、填空题
三、解答题
注意:本试卷分试题卷和答题卡两部分,考试时间100分钟,满分120
分.考生应首先阅读试题卷上的文字信息,然后在答题卡上作答,在试
题卷上作答无效,交卷时只交答题卡.
一、选择题
1. 的相反数是( )
A. 2025 B. C. D.
【分析】本题主要考查了求一个数的相反数,熟知只有符号不同的两
个数互为相反数,0的相反数是0是解题的关键.
【详解】解:的相反数是2025,
故选
√
2. 百米飞人大赛,裁判经常会依据视频作出正确
判断,则高空摄像机视角所看到的是运动员撞线的
( )
A. 主视图 B. 左视图 C. 俯视图 D. 右视图
【分析】本题考查的是三视图中俯视图的含义,此图是从上往下得到
的视图,由三视图的含义可得答案.
【详解】解:因为是百米赛跑,看谁先过线,高空摄像机视角是从上
往下得到的视图,该图主要反映了场上运动员的俯视图;
故选:
√
3. 河南许昌胖东来2024年春节假期4天接待游客144万人次,总游客量
超越了河南所有景区跃居榜首,有望成为一个4A级景区,144万用科学
记数法表示为( )
A. B. C. D.
【分析】本题主要考查了科学记数法的表示方法,熟练掌握科学记数
法的表示方法是解题的关键.确定的值时,要看把原数变成时,小数
点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值
大于等于10时,是正整数,当原数绝对值小于1时,是负整数;由
此进行求解即可得到答案.
√
【详解】解:144万,
故选:
4. 下列计算正确的是( )
A. B.
C. D.
【分析】根据合并同类项的法则,同底数幂的除法、乘法运算法则,
幂的乘方运算法则计算即可得出结论.
√
【详解】解:、与不是同类项,不能合并,该选项不符合题意;
B、,该选项不符合题意;
C、,该选项不符合题意;
D、,该选项符合题意;
故选:
【点睛】本题考查了合并同类项的运算法则,同底数幂的乘法、除法
运算法则以及幂的乘方的运算法则,熟记整式乘除法的相关运算法则
是解题的关键.
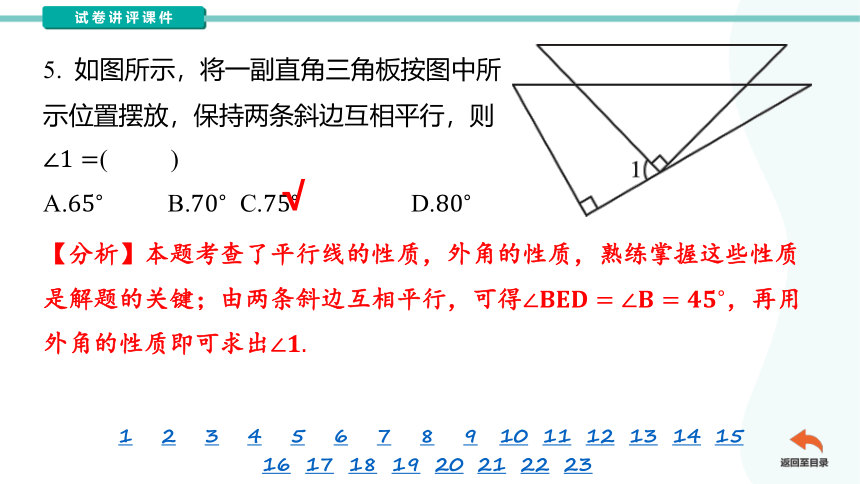
5. 如图所示,将一副直角三角板按图中所
示位置摆放,保持两条斜边互相平行,则
( )
A. B. C. D.
【分析】本题考查了平行线的性质,外角的性质,熟练掌握这些性质
是解题的关键;由两条斜边互相平行,可得,再用
外角的性质即可求出
√
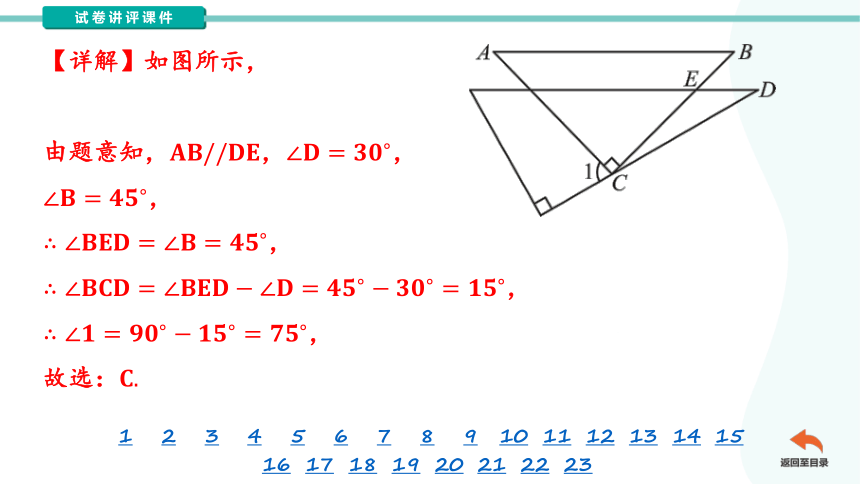
【详解】如图所示,
由题意知,,,
,
,
,
,
故选:
6. 关于的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
【分析】根据方程的根的判别式
判断即可.熟练掌握根的判
别式是解题的关键.
【详解】整理为一般式为,
,
方程有两个不等实根.
故选
√
7. 下表是韩梅参加演讲比赛的得分表,表格中“ ”部分被污损,她的
总得分是( )
韩梅 演讲内容 言语表达 形象风度
得分 80 95 80
权重
A. 86 B. C. D. 88
【分析】题目主要考查加权平均数的计算方法,理解题意是解题关键.
【详解】解:形象风度占比为,
总得分是:,
故选:
√
8. 小康和小明都是短视频爱好者,他们从近期火爆的A,B,C三个
主中随机选择一个关注,则两人关注的是同一个主的概率是( )
A. B. C. D.
【分析】本题考查了用列表法或画树状图法求概率.列表法或画树状图
法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成
的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:
概率所求情况数与总情况数之比.首先根据题意画出树状图,然后由
树状图求得所有等可能的结果以及两人关注的是同一个主的情况,
再利用概率公式求解即可求得答案.
√
【详解】解:根据题意画树状图为:
共有9种等可能的情况,其中两人关注的是同一个主的情况为3,
所以两人关注的是同一个主的概率,
故选:
9. 已知二次函数的图象如图所示,则
一次函数的图象大致为( )
A. B. C. D.
【分析】本题考查了二次函数系数与图象的关系以及一次函数与二次函
数的图象的综合判断,通过分析二次函数图象得到的符号是解题关键.
√
【详解】解:根据已知二次函数图象,抛物线开口向下,则可知,
由抛物线对称轴在y轴右侧,则对称轴为直线,
,
一次函数 图象经过第一、二、四象限,
故应选:
10. 如图所示,矩形的顶点为坐标原
点,,对角线在第二象限的角平分
线上.若矩形从图示位置开始绕点以每秒
的速度顺时针旋转,则第2025秒时,点的对
应坐标为( )
A. B.
C. D.
√
【分析】本题考查旋转变换,矩形的性质等知识,解题的关键是明确
题意,发现点的变化特点,利用数形结合的思想解答,每秒旋转,
则8次一个循环,,第2025秒时,点的对应点
落在轴正半轴上,由此可得到点的坐标.
【详解】解:四边形是矩形,
,
每秒旋转,8次一个循环,,
第2025秒时,点的对应点落在轴正半轴上,
点的坐标为
故选:
二、填空题
11. 若苹果每千克元,用元购买3千克的苹果,找零可用代数式表示
为_______________.
/
【分析】题目主要考查列代数式,理解题意是解题关键.根据题意列出
代数式即可.
【详解】解:已知苹果每千克元,可知3千克的苹果为元,
故找零为,
故答案为:
12. 关于的一元一次不等式组的解集是_________.
【分析】本题主要考查了解一元一次不等式组.先求出不等式组中每一
个不等式的解集,再求出它们的公共部分即可.
【详解】解:,
由①,得;
由②,得;
故不等式组的解集为
13. 如图所示,在菱形中,
,,垂足为,若
,则菱形周长为____.
40
【分析】本题考查了三角函数,菱形的性质,勾股定理,由三角函数
可得到边长比,再利用勾股定理设未知数列方程是解题的关键,由
,可得,设,由勾股定理得,再
由菱形的性质求解即可;
【详解】,
,
在中,
,
,
设,则,
由勾股定理得,
四边形 菱形,
,
,
菱形的周长
故答案为:40.
14. 如图所示,是半圆的直径,将直径
绕点顺时针旋转得对应线段,若,
则图中阴影部分的面积是______.
【分析】本题考查的是扇形面积的计算及图形
旋转的性质,连接,根据题意,用扇形
的面积减去扇形的面积,再减去的面积即可.
【详解】解:连接,
由旋转的性质得:,
由圆周角性质可得,
,
,
的面积,
扇形的面积,
扇形的面积,
阴影部分的面积 ,
故答案为:
15. 在矩形中,,点为射线上一点,将沿着
翻折,使得点 对应点落在射线上,若线段,连接
,则的值为____________.
或
【分析】本题考查了矩形的性质,正方形的判定
和性质,折叠的性质,勾股定理,根据性质,利
用勾股定理分类计算即可.
【详解】①如图1所示,点落在线段上,
矩形,
,
沿着翻折,使得点的对应点落在射线上,
,,
四边形为正方形,
,,
,
;
②如图2所示,点落在射线上,
矩形,
,
沿着翻折,使得点的对应点落在射线上,
,,
四边形为正方形,
,,
,
综上所述,的值为或
三、解答题
16.(1)计算:;
【答案】3;
先求出算术平方根及负整数指数幂、绝对值化简,然后计算加减法即可;
【详解】解:
;
(2)化简:
【答案】
先进行通分,然后计算加减法,再计算除法即可.
【详解】解:
【分析】题目主要考查实数的混合运算及分式的化简,熟练掌握运算法则
是解题关键.
17. 《少年急救官生命教育安全课》寒假第一课于2月1日以视频课的形
式开播.某校为了解学生观看视频课的时长,随机抽取了部分学生观看
视频课的时长(单位: 作为样本,将收集的数据整理后分为A,B,C,
D,E五个组别,其中A组的数据分别为:,绘制成如
下不完整的统计图表.
各组观看视频课时长频数分布表
组别 时间 频数
A 5
B 12
C
D 15
E 8
请根据以上信息回答下列问题:
(1)A组数据的众数是____,中位数是____;
0.2
0.3
【分析】利用中位数,众数的定义计算
即可;
【详解】,
众数是,中位数是,
(2)本次调查的样本容量是____,C组所在扇形的圆心角的大小是______;
60
【分析】利用D项目的人数除以其所占的百分比即可得到结论,利用
扇形的知识计算求解可得到结论;
根据题意,得 (人),
根据题意,得 (人),
,
故答案为:60,
(3)若该校有1800名学生,估计该校学生观看视频课时长超过的人数.
【答案】该校学生观看视频课时长超过的人数大约有690人
【分析】利用样本估计总体的思想计算即可.此题考查了扇形统计图,
频数分布表,读懂统计图,看懂分布表,从不同的统计表和统计图中
得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的
百分比大小.
根据题意,得 (人),
答:该校学生观看视频课时长超过的人数大约有690人.
故答案为:;
18. 已知及圆外一点A,连接线
段,请用无刻度直尺和圆规完成
操作并解答.
(1)过点A作出的两条切线,
,切点分别为点P、点Q;
(保留作图痕迹,不写作法和证明)
【答案】见解析
作的垂直平分线确定的中点,然后以中点为圆心,长为半
径作圆,交圆O于点P、Q,连接即可;
【详解】解:如图所示,,为所作.
(2)在(1)的条件下,若点E为优弧上不与端点重合的一点,且
,求的度数.
【答案】的度数为
连接,,根据圆周角定理确定,再由切
线的性质及圆内接四边求解即可.
【详解】连接,,如图所示
由圆周角定理知:
,为的两条切线,
,
【分析】题目主要考查切线及中垂线的作法,圆周角定理及圆内接四
边形的性质,理解题意,综合运用这些知识点是解题关键.
19. 如图所示,双曲线的图象与
一次函数的图象交于,
两点.
(1)求反比例函数的解析式;
【答案】
先求出点A的坐标,由点A的坐标,利用反比例函数图象上点的坐标特
征可求出的值,进而可得出反比例函数的解析式;
(2)观察图象,直接写出不等式的解集;
【答案】或
观察函数图象,根据两函数图象的上下位置关系,即可得出不等式的
解集;
(3)设直线与轴交于点C,若P为轴正半轴上一点,当的面积
为3时,求点P的坐标.
【答案】点的坐标为
【分析】本题是反比例函数的综合题,主要考查了待定系数法求函数
解析式,反比例函数图象上点的坐标特征,三角形的面积的计算,正
确利用数形结合分析是解题关键.
(3)求出C点的坐标,根据三角形的面积公式即可求出答案.
【详解】解:设直线交轴于,交轴于,
在中,当时,,
,
当时,,解得,
,
设点的坐标为,
,,
,
面积为3,
,解得,
点的坐标为;
20. 太阳能路灯目前已经成为节能环保的代名
词.某校学生开展综合实践活动,测量太阳能
路灯电池板顶端E点离地面的高度.如图所示,
已知测角仪的高度为米,在测点B处安置测
角仪,测得点E的仰角为,在与点B相距
【答案】电池板离地面的高度的长约为米
米的测点D处安置等高的测角仪,测得点E的仰角为 (点B,D与F
在一条直线上),求电池板离地面的高度的长.(结果精确到米;参
考数据:,,,)
【分析】题目主要考查解三角形的应用,理解题意,作出辅助线,熟
练掌握运用解三角形的方法是解题关键.延长交于点,根据等腰
三角形的判定和性质得出为等腰直角三角形,设米,根
据正切函数的定义求解即可.
【详解】解:延长交于点,
由题意得:米,
设米,
,,
为等腰直角三角形,
米,
米,
在中,,
解得,
(米).
电池板离地面的高度的长约为8.1米.
21. 2024年春节假日期间,33万余名游客欢聚云台山,新春喜乐会年味
足.焦作某知名小吃店计划购买A,B两种食材制作小吃,宾飨游客.已
知购买1千克A种食材和2千克B种食材共需49元,购买2千克A种食材和
1千克B种食材共需53元.
(1)求A,B两种食材的单价;
【答案】A种食材的单价是每千克19元,B种食材的单价是每千克15元
设A种食材的单价为元/千克,B种食材的单价为元/千克.根据题意列
出方程组,并解出方程组的解,即可作答.
【详解】解:设A种食材的单价为元/千克,B种食材的单价为元/千
克.
根据题意,得
解得
A种食材的单价是每千克19元,B种食材的单价是每千克15元.
(2)该小吃店计划购买两种食材共48千克,其中购买A种食材千克数不
少于B种食材千克数的3倍,当A,B两种食材分别购买多少千克时,总
费用最少?并求出最少总费用.
【答案】A种食材购买36千克,B种食材购买12千克时,总费用最少,
为864元
设A种食材购买千克,则B种食材购买千克,总费用为元,
依题意,得,根据“购买A种食材千克数不少于B种食材
千克数 3倍,”得,即可作答.
【详解】解:设A种食材购买千克,则B种食材购买千克,
总费用为元.
根据题意,得
,
,
随的增大而增大.
当时,有最小值为: (元).
A种食材购买36千克,B种食材购买12千克时,总费用最少,为864元
【分析】本题考查了二元一次方程组的应用,一次函数的应用,正确
掌握相关性质内容是解题的关键.
22. 在平面直角坐标系中,抛物线经过点,
(1)求抛物线的解析式;
【答案】
【详解】抛物线经过点,,
,
解得,
抛物线的解析式为;
(2)直线经过点A,判断点B是否在直线上,并说明
理由;
【答案】点不在直线上,见解析
【详解】点不在直线上.
理由:直线经过点,
,
解得,
所以直线解析式为
把代入,得,
点不在直线上;
(3)平移抛物线使其顶点仍在直线上,若平
移后抛物线与轴交点的纵坐标为,求的取值范围.
【答案】
【详解】平移抛物线,其顶点仍在直线上,
设平移后的抛物线的解析式为,
设平移后所得抛物线与轴交点的纵坐标为,则
的取值范围为
【分析】本题主要考查了待定系数法求二次函数和一次函数关系式,
根据二次函数的顶点式求最值,对于(1),将两个点的坐标代入关系式,
再求出解即可;
对于(2),将点A的坐标代入求出直线关系式,再将点B的横坐标代入说
明即可;
对于(3),由题意将顶点坐标代入顶点式,再将平移后的坐标
代入,并讨论即可.
23. 在等腰中,,顶角度数为,点是平面内一点,
连接,将线段绕点顺时针旋转得到线段,连接,,
(1)如图1所示,当时,请直接写出线段与的数量关系:
_________;
【分析】由旋转性质,得,,证明和
都是等边三角形,由其性质,证明,即
可作答.
【分析】、(2)的结论,易得四边形是矩形,根据勾股定理,得
,代入数值进行计算,即可作答.
【详解】解:
如图1所示,
将线段绕点顺时针旋转得到线段,
,
和都是等边三角形
,,
(2)如图2所示,当时,(1)中的结论还成立吗,并说明理由;
【答案】不成立,见解析
【分析】同理,证明和都是等腰直角三角形,然后根据
夹角相等,两边成比例证明,再结合相似三角形的性
质,即可作答.
【详解】解:不成立,
理由:如图2所示,
将线段绕点顺时针旋转得到线段,
,
,
和都是等腰直角三角形
,,
,
(3)在(2)的前提下,若,,,请直接写出线段
的长.
【答案】的长为或
【分析】结合
【详解】解:过作交所在直线于
如图1所示,由(2)知,
易得四边形是矩形,
设,则
在中,,
可得方程:,
解得
;
如图2所示,易得四边形是矩形,设,则
在中,,
可得方程:,解得
综上所述,的长为或
【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与
性质,勾股定理,等边三角形的性质,矩形的性质,综合性较强,难
度适中,正确掌握相关性质内容是解题的关键.
2024年河南省中考模拟试卷
数学
主讲人:某某某老师
某某学校
一、选择题
二、填空题
三、解答题
一、选择题
二、填空题
三、解答题
注意:本试卷分试题卷和答题卡两部分,考试时间100分钟,满分120
分.考生应首先阅读试题卷上的文字信息,然后在答题卡上作答,在试
题卷上作答无效,交卷时只交答题卡.
一、选择题
1. 的相反数是( )
A. 2025 B. C. D.
【分析】本题主要考查了求一个数的相反数,熟知只有符号不同的两
个数互为相反数,0的相反数是0是解题的关键.
【详解】解:的相反数是2025,
故选
√
2. 百米飞人大赛,裁判经常会依据视频作出正确
判断,则高空摄像机视角所看到的是运动员撞线的
( )
A. 主视图 B. 左视图 C. 俯视图 D. 右视图
【分析】本题考查的是三视图中俯视图的含义,此图是从上往下得到
的视图,由三视图的含义可得答案.
【详解】解:因为是百米赛跑,看谁先过线,高空摄像机视角是从上
往下得到的视图,该图主要反映了场上运动员的俯视图;
故选:
√
3. 河南许昌胖东来2024年春节假期4天接待游客144万人次,总游客量
超越了河南所有景区跃居榜首,有望成为一个4A级景区,144万用科学
记数法表示为( )
A. B. C. D.
【分析】本题主要考查了科学记数法的表示方法,熟练掌握科学记数
法的表示方法是解题的关键.确定的值时,要看把原数变成时,小数
点移动了多少位,的绝对值与小数点移动的位数相同,当原数绝对值
大于等于10时,是正整数,当原数绝对值小于1时,是负整数;由
此进行求解即可得到答案.
√
【详解】解:144万,
故选:
4. 下列计算正确的是( )
A. B.
C. D.
【分析】根据合并同类项的法则,同底数幂的除法、乘法运算法则,
幂的乘方运算法则计算即可得出结论.
√
【详解】解:、与不是同类项,不能合并,该选项不符合题意;
B、,该选项不符合题意;
C、,该选项不符合题意;
D、,该选项符合题意;
故选:
【点睛】本题考查了合并同类项的运算法则,同底数幂的乘法、除法
运算法则以及幂的乘方的运算法则,熟记整式乘除法的相关运算法则
是解题的关键.
5. 如图所示,将一副直角三角板按图中所
示位置摆放,保持两条斜边互相平行,则
( )
A. B. C. D.
【分析】本题考查了平行线的性质,外角的性质,熟练掌握这些性质
是解题的关键;由两条斜边互相平行,可得,再用
外角的性质即可求出
√
【详解】如图所示,
由题意知,,,
,
,
,
,
故选:
6. 关于的一元二次方程的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
【分析】根据方程的根的判别式
判断即可.熟练掌握根的判
别式是解题的关键.
【详解】整理为一般式为,
,
方程有两个不等实根.
故选
√
7. 下表是韩梅参加演讲比赛的得分表,表格中“ ”部分被污损,她的
总得分是( )
韩梅 演讲内容 言语表达 形象风度
得分 80 95 80
权重
A. 86 B. C. D. 88
【分析】题目主要考查加权平均数的计算方法,理解题意是解题关键.
【详解】解:形象风度占比为,
总得分是:,
故选:
√
8. 小康和小明都是短视频爱好者,他们从近期火爆的A,B,C三个
主中随机选择一个关注,则两人关注的是同一个主的概率是( )
A. B. C. D.
【分析】本题考查了用列表法或画树状图法求概率.列表法或画树状图
法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成
的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:
概率所求情况数与总情况数之比.首先根据题意画出树状图,然后由
树状图求得所有等可能的结果以及两人关注的是同一个主的情况,
再利用概率公式求解即可求得答案.
√
【详解】解:根据题意画树状图为:
共有9种等可能的情况,其中两人关注的是同一个主的情况为3,
所以两人关注的是同一个主的概率,
故选:
9. 已知二次函数的图象如图所示,则
一次函数的图象大致为( )
A. B. C. D.
【分析】本题考查了二次函数系数与图象的关系以及一次函数与二次函
数的图象的综合判断,通过分析二次函数图象得到的符号是解题关键.
√
【详解】解:根据已知二次函数图象,抛物线开口向下,则可知,
由抛物线对称轴在y轴右侧,则对称轴为直线,
,
一次函数 图象经过第一、二、四象限,
故应选:
10. 如图所示,矩形的顶点为坐标原
点,,对角线在第二象限的角平分
线上.若矩形从图示位置开始绕点以每秒
的速度顺时针旋转,则第2025秒时,点的对
应坐标为( )
A. B.
C. D.
√
【分析】本题考查旋转变换,矩形的性质等知识,解题的关键是明确
题意,发现点的变化特点,利用数形结合的思想解答,每秒旋转,
则8次一个循环,,第2025秒时,点的对应点
落在轴正半轴上,由此可得到点的坐标.
【详解】解:四边形是矩形,
,
每秒旋转,8次一个循环,,
第2025秒时,点的对应点落在轴正半轴上,
点的坐标为
故选:
二、填空题
11. 若苹果每千克元,用元购买3千克的苹果,找零可用代数式表示
为_______________.
/
【分析】题目主要考查列代数式,理解题意是解题关键.根据题意列出
代数式即可.
【详解】解:已知苹果每千克元,可知3千克的苹果为元,
故找零为,
故答案为:
12. 关于的一元一次不等式组的解集是_________.
【分析】本题主要考查了解一元一次不等式组.先求出不等式组中每一
个不等式的解集,再求出它们的公共部分即可.
【详解】解:,
由①,得;
由②,得;
故不等式组的解集为
13. 如图所示,在菱形中,
,,垂足为,若
,则菱形周长为____.
40
【分析】本题考查了三角函数,菱形的性质,勾股定理,由三角函数
可得到边长比,再利用勾股定理设未知数列方程是解题的关键,由
,可得,设,由勾股定理得,再
由菱形的性质求解即可;
【详解】,
,
在中,
,
,
设,则,
由勾股定理得,
四边形 菱形,
,
,
菱形的周长
故答案为:40.
14. 如图所示,是半圆的直径,将直径
绕点顺时针旋转得对应线段,若,
则图中阴影部分的面积是______.
【分析】本题考查的是扇形面积的计算及图形
旋转的性质,连接,根据题意,用扇形
的面积减去扇形的面积,再减去的面积即可.
【详解】解:连接,
由旋转的性质得:,
由圆周角性质可得,
,
,
的面积,
扇形的面积,
扇形的面积,
阴影部分的面积 ,
故答案为:
15. 在矩形中,,点为射线上一点,将沿着
翻折,使得点 对应点落在射线上,若线段,连接
,则的值为____________.
或
【分析】本题考查了矩形的性质,正方形的判定
和性质,折叠的性质,勾股定理,根据性质,利
用勾股定理分类计算即可.
【详解】①如图1所示,点落在线段上,
矩形,
,
沿着翻折,使得点的对应点落在射线上,
,,
四边形为正方形,
,,
,
;
②如图2所示,点落在射线上,
矩形,
,
沿着翻折,使得点的对应点落在射线上,
,,
四边形为正方形,
,,
,
综上所述,的值为或
三、解答题
16.(1)计算:;
【答案】3;
先求出算术平方根及负整数指数幂、绝对值化简,然后计算加减法即可;
【详解】解:
;
(2)化简:
【答案】
先进行通分,然后计算加减法,再计算除法即可.
【详解】解:
【分析】题目主要考查实数的混合运算及分式的化简,熟练掌握运算法则
是解题关键.
17. 《少年急救官生命教育安全课》寒假第一课于2月1日以视频课的形
式开播.某校为了解学生观看视频课的时长,随机抽取了部分学生观看
视频课的时长(单位: 作为样本,将收集的数据整理后分为A,B,C,
D,E五个组别,其中A组的数据分别为:,绘制成如
下不完整的统计图表.
各组观看视频课时长频数分布表
组别 时间 频数
A 5
B 12
C
D 15
E 8
请根据以上信息回答下列问题:
(1)A组数据的众数是____,中位数是____;
0.2
0.3
【分析】利用中位数,众数的定义计算
即可;
【详解】,
众数是,中位数是,
(2)本次调查的样本容量是____,C组所在扇形的圆心角的大小是______;
60
【分析】利用D项目的人数除以其所占的百分比即可得到结论,利用
扇形的知识计算求解可得到结论;
根据题意,得 (人),
根据题意,得 (人),
,
故答案为:60,
(3)若该校有1800名学生,估计该校学生观看视频课时长超过的人数.
【答案】该校学生观看视频课时长超过的人数大约有690人
【分析】利用样本估计总体的思想计算即可.此题考查了扇形统计图,
频数分布表,读懂统计图,看懂分布表,从不同的统计表和统计图中
得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的
百分比大小.
根据题意,得 (人),
答:该校学生观看视频课时长超过的人数大约有690人.
故答案为:;
18. 已知及圆外一点A,连接线
段,请用无刻度直尺和圆规完成
操作并解答.
(1)过点A作出的两条切线,
,切点分别为点P、点Q;
(保留作图痕迹,不写作法和证明)
【答案】见解析
作的垂直平分线确定的中点,然后以中点为圆心,长为半
径作圆,交圆O于点P、Q,连接即可;
【详解】解:如图所示,,为所作.
(2)在(1)的条件下,若点E为优弧上不与端点重合的一点,且
,求的度数.
【答案】的度数为
连接,,根据圆周角定理确定,再由切
线的性质及圆内接四边求解即可.
【详解】连接,,如图所示
由圆周角定理知:
,为的两条切线,
,
【分析】题目主要考查切线及中垂线的作法,圆周角定理及圆内接四
边形的性质,理解题意,综合运用这些知识点是解题关键.
19. 如图所示,双曲线的图象与
一次函数的图象交于,
两点.
(1)求反比例函数的解析式;
【答案】
先求出点A的坐标,由点A的坐标,利用反比例函数图象上点的坐标特
征可求出的值,进而可得出反比例函数的解析式;
(2)观察图象,直接写出不等式的解集;
【答案】或
观察函数图象,根据两函数图象的上下位置关系,即可得出不等式的
解集;
(3)设直线与轴交于点C,若P为轴正半轴上一点,当的面积
为3时,求点P的坐标.
【答案】点的坐标为
【分析】本题是反比例函数的综合题,主要考查了待定系数法求函数
解析式,反比例函数图象上点的坐标特征,三角形的面积的计算,正
确利用数形结合分析是解题关键.
(3)求出C点的坐标,根据三角形的面积公式即可求出答案.
【详解】解:设直线交轴于,交轴于,
在中,当时,,
,
当时,,解得,
,
设点的坐标为,
,,
,
面积为3,
,解得,
点的坐标为;
20. 太阳能路灯目前已经成为节能环保的代名
词.某校学生开展综合实践活动,测量太阳能
路灯电池板顶端E点离地面的高度.如图所示,
已知测角仪的高度为米,在测点B处安置测
角仪,测得点E的仰角为,在与点B相距
【答案】电池板离地面的高度的长约为米
米的测点D处安置等高的测角仪,测得点E的仰角为 (点B,D与F
在一条直线上),求电池板离地面的高度的长.(结果精确到米;参
考数据:,,,)
【分析】题目主要考查解三角形的应用,理解题意,作出辅助线,熟
练掌握运用解三角形的方法是解题关键.延长交于点,根据等腰
三角形的判定和性质得出为等腰直角三角形,设米,根
据正切函数的定义求解即可.
【详解】解:延长交于点,
由题意得:米,
设米,
,,
为等腰直角三角形,
米,
米,
在中,,
解得,
(米).
电池板离地面的高度的长约为8.1米.
21. 2024年春节假日期间,33万余名游客欢聚云台山,新春喜乐会年味
足.焦作某知名小吃店计划购买A,B两种食材制作小吃,宾飨游客.已
知购买1千克A种食材和2千克B种食材共需49元,购买2千克A种食材和
1千克B种食材共需53元.
(1)求A,B两种食材的单价;
【答案】A种食材的单价是每千克19元,B种食材的单价是每千克15元
设A种食材的单价为元/千克,B种食材的单价为元/千克.根据题意列
出方程组,并解出方程组的解,即可作答.
【详解】解:设A种食材的单价为元/千克,B种食材的单价为元/千
克.
根据题意,得
解得
A种食材的单价是每千克19元,B种食材的单价是每千克15元.
(2)该小吃店计划购买两种食材共48千克,其中购买A种食材千克数不
少于B种食材千克数的3倍,当A,B两种食材分别购买多少千克时,总
费用最少?并求出最少总费用.
【答案】A种食材购买36千克,B种食材购买12千克时,总费用最少,
为864元
设A种食材购买千克,则B种食材购买千克,总费用为元,
依题意,得,根据“购买A种食材千克数不少于B种食材
千克数 3倍,”得,即可作答.
【详解】解:设A种食材购买千克,则B种食材购买千克,
总费用为元.
根据题意,得
,
,
随的增大而增大.
当时,有最小值为: (元).
A种食材购买36千克,B种食材购买12千克时,总费用最少,为864元
【分析】本题考查了二元一次方程组的应用,一次函数的应用,正确
掌握相关性质内容是解题的关键.
22. 在平面直角坐标系中,抛物线经过点,
(1)求抛物线的解析式;
【答案】
【详解】抛物线经过点,,
,
解得,
抛物线的解析式为;
(2)直线经过点A,判断点B是否在直线上,并说明
理由;
【答案】点不在直线上,见解析
【详解】点不在直线上.
理由:直线经过点,
,
解得,
所以直线解析式为
把代入,得,
点不在直线上;
(3)平移抛物线使其顶点仍在直线上,若平
移后抛物线与轴交点的纵坐标为,求的取值范围.
【答案】
【详解】平移抛物线,其顶点仍在直线上,
设平移后的抛物线的解析式为,
设平移后所得抛物线与轴交点的纵坐标为,则
的取值范围为
【分析】本题主要考查了待定系数法求二次函数和一次函数关系式,
根据二次函数的顶点式求最值,对于(1),将两个点的坐标代入关系式,
再求出解即可;
对于(2),将点A的坐标代入求出直线关系式,再将点B的横坐标代入说
明即可;
对于(3),由题意将顶点坐标代入顶点式,再将平移后的坐标
代入,并讨论即可.
23. 在等腰中,,顶角度数为,点是平面内一点,
连接,将线段绕点顺时针旋转得到线段,连接,,
(1)如图1所示,当时,请直接写出线段与的数量关系:
_________;
【分析】由旋转性质,得,,证明和
都是等边三角形,由其性质,证明,即
可作答.
【分析】、(2)的结论,易得四边形是矩形,根据勾股定理,得
,代入数值进行计算,即可作答.
【详解】解:
如图1所示,
将线段绕点顺时针旋转得到线段,
,
和都是等边三角形
,,
(2)如图2所示,当时,(1)中的结论还成立吗,并说明理由;
【答案】不成立,见解析
【分析】同理,证明和都是等腰直角三角形,然后根据
夹角相等,两边成比例证明,再结合相似三角形的性
质,即可作答.
【详解】解:不成立,
理由:如图2所示,
将线段绕点顺时针旋转得到线段,
,
,
和都是等腰直角三角形
,,
,
(3)在(2)的前提下,若,,,请直接写出线段
的长.
【答案】的长为或
【分析】结合
【详解】解:过作交所在直线于
如图1所示,由(2)知,
易得四边形是矩形,
设,则
在中,,
可得方程:,
解得
;
如图2所示,易得四边形是矩形,设,则
在中,,
可得方程:,解得
综上所述,的长为或
【点睛】本题考查了全等三角形的判定与性质、相似三角形的判定与
性质,勾股定理,等边三角形的性质,矩形的性质,综合性较强,难
度适中,正确掌握相关性质内容是解题的关键.
同课章节目录
