2024年云南省云天化中学九年级学业水平考试数学模拟(一)讲评课件(共70张PPT)
文档属性
| 名称 | 2024年云南省云天化中学九年级学业水平考试数学模拟(一)讲评课件(共70张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览











文档简介
(共70张PPT)
二二四年初中学业水平模拟考试
数学试题卷(一)
主讲人:某某某老师
某某学校
一、选择题
二、填空题
三、解答题
一、选择题
二、填空题
三、解答题
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的
相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题
1. 珠穆朗玛峰是世界最高的山峰,某日测得山脚气温为,山顶气
温为,则山脚与山顶的温度差为( )
A. B. C. D.
【分析】此题主要考查了有理数的减法运算的应用,正确掌握相关运
算法则是解题关键.直接利用有理数的减法运算法则计算得出答案.
【详解】解:山脚气温为,山顶气温为,
山脚与山顶的温度相差为:
故选:
√
2. 我国自主研发的口径球面射电望远镜有“中国天眼”之称,
它的反射面面积约为,用科学记数法表示数据250000为 ( )
A. B. C. D.
【分析】本题主要考查了科学记数法表示绝对值大于1的数,先确定
,,再写成形如的形式即可.
【详解】
故选:
√
3. 如图,直线与直线都相交.若,
,则 ( )
A. B. C. D.
【分析】本题考查平行线的性质,根据两直线平行
同位角相等结合対顶角相等即可得到答案
√
【详解】解:,,
,
,
,
故选:
4. 若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这
个几何体是( )
A. 球体 B. 圆锥 C. 圆柱 D. 正方体
【分析】利用三视图都是圆,则可得出几何体的形状.
【详解】主视图、俯视图和左视图都是圆的几何体是球,
故选
【点睛】本题考查了由三视图确定几何体的形状,熟悉常见几何体的
三视图是解题的关键.
√
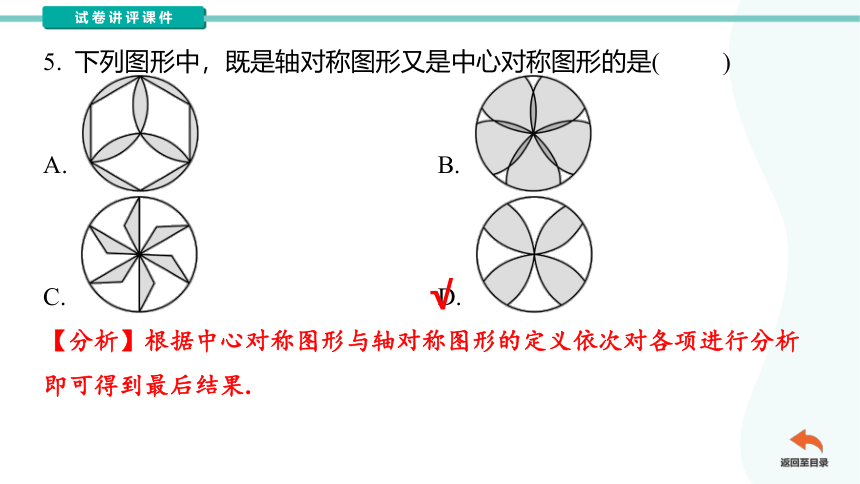
5. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形与轴对称图形的定义依次对各项进行分析
即可得到最后结果.
√
【详解】解:A、此图形沿一条直线对折后能够完全重合,此图形是
轴对称图形,但不是中心对称图形,故此选项错误;
B、此图形沿一条直线对折后能够完全重合,此图形是轴对称图形,但
不是中心对称图形,故此选项错误;
C、此图形沿一条直线对折后不能够完全重合,此图形不是轴对称图
形,故此选项错误;
D、此图形沿一条直线对折后能够完全重合,此图形是轴对称图形,
旋转能够与原图形重合,是中心对称图形,故此选项正确.
故选:D.
【点睛】本题主要考查了中心对称图形与轴对称图形的概念,熟练掌
握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫
做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转
后能够与自身重合,那么这个图形就叫做中心对称图形,这个点
叫做对称中心,是解答本题的关键.
6. 若关于的一元二次方程有两个不相等的实数根,
则实数的取值范围是( )
A. B.
C. 且 D. 且
【分析】本题考查了根的判别式:一元二次方程
的根与有如下关系:当时,
方程有两个不相等的实数根;当时,方程有两个相等的实数根;
当时,方程无实数根.根据一元二次方程的定义和判别式的意义得
到且,然后求出两不等式的公共部分即可.
√
【详解】解:根据题意得且,
解得且
故选:
7. 十二边形的内角和为( )
A. B. C. D.
【分析】本题考查多边形的内角和定理,根据边形的内角和为
计算即可即可得到答案;
【详解】解:由题意可得,
,
故选:
√
8. 下列计算正确的是( )
A. B.
C. D.
【分析】本题考查同底数幂的乘法,除法及合并同类项,根据
,,,
求解即可得到答案;
√
【详解】解:由题意可得,
,故A不正确,不符合题意,
,故B不正确,不符合题意,
,故C正确,符合题意,
,故D不正确,不符合题意,
故选:
9. 一次空气污染指数抽查中,收集到9天的数据如下:60,70,70,56,81,
91,92,91,75.该组数据的中位数是( )
A. 70 B. 81 C. 91 D. 75
【分析】本题考查了确定一组数据的中位数的能力.注意找中位数的时
候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果
数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两
位数的平均数.找中位数要把数据按从小到大的顺序排列,位于最中间
的一个数(或两个数的平均数)为中位数.
√
【详解】解:将这组数据重新排序为:56、60、70、70、75、81、91、
91、92,
则其中位数为75,
故选:
10. 已知为两个连续整数,且,则等于( )
A. 5 B. 7 C. 9 D. 11
【分析】本题考查了无理数的估算,代数式求值,先估算出的取值
范围,得出的大小,代入求值即可.
【详解】解:,
,
为两个连续整数,且,
,,
,
故选:
√
11. 某商品经过两次连续降价,每件售价由原来的100元降到了81元.设
平均每次降价的百分率为,则下列方程中正确的是( )
A. B.
C. D.
【分析】设平均每次降价的百分率为,可先表示出第一次降价后的价
格,那么第一次降价后的价格降价的百分率,把相应数
值代入即可求解.根据题意列出一元二次方程即可;
√
【详解】解:设平均每次降价的百分率为,根据题意,第一降价后的价
格为,第二次降价后的价格为,即:
故选C
【点睛】本题考查了一元二次方程的应用,理解题意列出方程是解题
的关键.
12. 按一定规律排列的单项式:,,,,,,,
第个单项式是( )
A. B. C. D.
【分析】先分析前面所给出的单项式,从三方面(符号、系数的绝对值、
指数)总结规律,发现规律进行概括即可得到答案.
【详解】解: ,,,,,,,
可记为:
第项为:
故选
√
【点睛】本题考查了单项式的知识,分别找出单项式的系数和次数的
规律是解决此类问题的关键.
13. 对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2
分,3分,
4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据
图中信息,这些学生的平均分数
是【 】( )
A. 2.25 B. 2.5 C. 2.95 D. 3
√
【详解】扇形统计图,条形统计图,频数、频率和总量的关系,加权
平均数.
由得4分的频数12,频率,得总量
由得3分的频率,得频数
由得1 分的频数3,得频率
得2分的频率为
这些学生的平均分数是:
故选
14. 已知都在反比例函数的图
象上,则的关系是( )
A. B. C. D.
【分析】本题考查了反比例函数 性质,根据反比例函数的性质先得
到当时,函数值的大小,然后跟时函数值的大小作比较即可,
掌握反比例函数的性质是解题的关键.
√
【详解】解:反比例函数,
当时,随的增大而减小,当时随的增大而减小,
,
,
,
,
即,
故选:
15. 如图,四边形内接于,的半径为
4,,则的长是( )
A. B. C. D.
【分析】本题考查圆内解四边形对角互补及扇形弧
长公式,根据得到,从而得到,
结合求解即可得到答案;
√
【详解】解:四边形内接于,
,
,
,
,
故选:
二、填空题
16. 使有意义的的取值范围为____________.
/
【分析】本题考查了二次根式有意义 条件:二次根式中的被开方数
必须是非负数,否则二次根式无意义.根据被开方数大于等于0列式计
算即可得解.
【详解】解:有意义,
,
解得:,
故答案为:
17. 分解因式:______________________________.
/
【分析】本题考查因式分解,先提取公因式,再根据平方差公式分解
即可得到答案;
【详解】解:,
故答案为:
18. 如图,在中,点D、E分别是、
边的中点,则______.
/0 5
【分析】根据三角形中位线的性质即可解答.
【详解】点D、E分别是、边的中点
故答案为:
【点睛】本题考查了三角形中位线的性质,熟练掌握上述知识点是解
答本题的关键.
19. 已知圆锥的母线长是10,侧面积是,则此圆锥的高是___.
8
【分析】本题考查了圆锥的计算,一元一次方程的应用,勾股定理,
设圆锥的底面半径为,根据侧面积公式列方程求出半径,再根据勾
股定理进行求解即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
圆锥的高,
故答案为:8.
三、解答题
20. 计算:
【答案】8
【分析】本题考查了二次根式的混合远算、绝对值化简、负整数指数
幂、特殊角的三角函数等知识,分别根据二次根式的乘法、绝对值、
负整数指数幂,特殊角三角函数等知识化简,再进行计算即可求解.
【详解】解:
21. 如图,点、在线段上,
,,且 求证:
【答案】见解析
【分析】本题主要考查了全等三角形的判定与性质,平行线的性质,
解题的关键是掌握全等三角形的判定与性质.根据可得
,由,推出,结合已知可证明
,最后根据全等三角形的性质即可求解.
【详解】证明:,
,
,
,
即,
,
在和中,
,
,
22. 某城市出租车起步价行驶的最远路程为3千米,超过3千米的部分按
每千米另收费,甲说:“我乘这种出租车走了5千米,付了9元”;乙说:
“我乘这种出租车走了7千米,付了12元”.请你算一算这种出租车的起步
价是多少元?以及超过3千米后,每千米的车费是多少元?
【答案】这种出租车的起步价是6元,超过3千米后,每千米的车费是1.
5元.
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列
出二元一次方程组是解题的关键.
设这种出租车的起步价是元,超过3千米后,每千米的车费是元,根
据题中的等量关系即可列出二元一次方程组,
【详解】解:设这种出租车的起步价是元,超过3千米后,每千米的
车费是元,
由题意得:,
解得:,
答:这种出租车的起步价是6元,超过3千米后,每千米的车费是1.5元.
23. 某单位决定从甲、乙、丙、丁四名员工中选取两人到社区当志愿者.
现将四名员工的名字分别写在四张完全相同且不透明卡片的正面,把
四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片记
下名字,再从剩余的三张卡片中随机抽取一张卡片,记下名字.
(1)从四张卡片中随机抽取一张,恰好是甲员工的概率为______;
利用概率公式求解即可;
【详解】解:从四张卡片中随机抽取一张,恰好是甲员工的概率为;
第一次 第二次 甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
共有12个等可能的结果,其中抽签活动中A,B两名志愿者被同时选中
的有2种结果,所以抽签活动中甲、乙两名员工同时被抽中的概率为
答:甲、乙两名员工同时被抽中的概率
(2)请用列表或画树状图的方法,求出甲、乙两名员工同时被抽中的概率.
画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据
概率公式求解即可.
【分析】本题考查的是用列表法或画树状图法求概率.列表法或画树状
图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事
件;树状图法适合两步或两步以上完成的事件;注意概率所求情况
数与总情况数之比.
24. 新能源汽车有着动力强油耗低的特点正逐渐成为人们喜爱的交通工
具.某汽车4S店决定采购新能源甲型和乙型两款汽车,已知每辆甲型汽
车的进价是每辆乙型汽车的进价的倍,若用1800万元购进甲型汽车
的数量比1400万元购进乙型汽车的数量多10辆.
(1)甲型和乙型汽车的进价分别为每辆多少万元?
【答案】甲型汽车的进价为每辆12万元,乙型汽车的进价为每辆10万元;
设乙型汽车的进价为每辆万元,则甲型汽车的进价为每辆万元,
再利用用1800万元购进甲型汽车的数量比1400万元购进乙型汽车的数
量多10辆,再建立方程求解即可;
【详解】解:设乙型汽车的进价为每辆万元,则甲型汽车的进价为每
辆万元,
依题意得:,
解得:,
经检验,是方程的解,,
答:甲型汽车的进价为每辆12万元,乙型汽车的进价为每辆10万元;
(2)该公司决定用不多于1120万元购进甲型和乙型汽车共100辆,最多可
以购买多少辆甲型汽车?
【答案】最多可以购买60辆甲型汽车.
设购买辆甲型汽车,则购买辆乙型汽车,利用公司决定用
不多于1120万元购进甲型和乙型汽车共100辆,再建立不等式解题即可.
【详解】解:设购买辆甲型汽车,则购买辆乙型汽车,
依题意得:
解得:,
答:最多可以购买60辆甲型汽车.
【分析】本题考查的是分式方程的应用,一元一次不等式的应用,理
解题意,确定相等关系与不等关系是解本题的关键;
25. 如图,在矩形中,的垂直平分线分
别交于,连接
(1)求证:四边形是菱形;
【答案】详见解析
先证明四边形是平行四边形,再证明,从而可得结论;
【详解】证明:四边形是矩形,是的中点,
,
,
又,
在和中,
,
,且
四边形是平行四边形,
垂直平分
四边形是菱形;
(2)若,求四边形的面积.
【答案】5
利用菱形的性质与勾股定理求解,再求解面积即可.
【详解】四边形是菱形
,
在中,,
,
四边形的面积
【分析】本题考查的是矩形的性质,菱形的判定与性质,熟练的证明
四边形是菱形是解本题的关键;
26. 在平面直角坐标系中,如果点的横坐标和纵坐标相等,则称点
为和谐点,例如:点,,都是和谐点.
(1)判断函数 图象上是否存在和谐点,若存在,求出其和
谐点的坐标;
【答案】
【详解】解:点的横坐标和纵坐标相等,则称点为和谐点,
和谐点都在上,,
解得,
图象上的和谐点为;
(2)若二次函数的图象上有且只有一个和谐点
当时,函数的最小值为
,最大值为0,求实数的取值范围.
【答案】
【详解】解:二次函数的图象上有且只有一
个和谐点,
,即有两个相等的实数根,
,
解得①,
将代入得,
②,
联立①②,得,,
,
其顶点坐标为,则最小值为,
根据对称轴可知,当时,,
根据函数图象可知,当时,函数的最小
值为,最大值为0,
实数的取值范围为
【分析】本题考查二次函数与一次函数的关系,一次函数与一次函数
交点问题:
(1)根据和谐点定义得到点在上,联合求解即可得到答
案;
(2)根据和谐点联立二次函数与一次函数求解即可得到答案;
27. 如图,是的直径,点是劣弧
上一点,,且平
分与交于点
(1)求证:是的切线;
【答案】详见解析
【分析】根据是的直径,可得,即
,根据同弧所对的圆周角相等,以及已知条件可
得,等量代换后即可得,进而得证;
【详解】证明:是的直径,
,
,
,
,
,
,
,
即,
又是的直径
是的切线;
(2)若,求的长;
【答案】
【分析】连接,根据角平分线的定义,以及等边对等角可得
,根据同弧所对的圆周角相等可得,由垂径定
理可得,进而可得,即可求解.
【详解】如图,连接,
平分,
,
是的直径,
,
即,
,
,
,
;
(3)延长交于点,若,求的半径.
【答案】的半径为
【分析】过点作,根据平行线分线段成比例,求得,
设的半径为,则,证明,可得
,在中,,勾股定理建立方程,
解方程即可求解.
【详解】如图,过点作,交于
..
,
,
平分,
,
,
,
,
,
设 半径为,则,
,
,
,
,
,
,
,
在中,
,
在中,,
即,
解得: (负值舍去),
的半径为
【点睛】本题考查了切线的判定,圆周角定理的推论,平行线分线段
成比例,相似三角形的性质与判定,解直角三角形,综合运用以上知
识是解题的关键.
二二四年初中学业水平模拟考试
数学试题卷(一)
主讲人:某某某老师
某某学校
一、选择题
二、填空题
三、解答题
一、选择题
二、填空题
三、解答题
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的
相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题
1. 珠穆朗玛峰是世界最高的山峰,某日测得山脚气温为,山顶气
温为,则山脚与山顶的温度差为( )
A. B. C. D.
【分析】此题主要考查了有理数的减法运算的应用,正确掌握相关运
算法则是解题关键.直接利用有理数的减法运算法则计算得出答案.
【详解】解:山脚气温为,山顶气温为,
山脚与山顶的温度相差为:
故选:
√
2. 我国自主研发的口径球面射电望远镜有“中国天眼”之称,
它的反射面面积约为,用科学记数法表示数据250000为 ( )
A. B. C. D.
【分析】本题主要考查了科学记数法表示绝对值大于1的数,先确定
,,再写成形如的形式即可.
【详解】
故选:
√
3. 如图,直线与直线都相交.若,
,则 ( )
A. B. C. D.
【分析】本题考查平行线的性质,根据两直线平行
同位角相等结合対顶角相等即可得到答案
√
【详解】解:,,
,
,
,
故选:
4. 若一个几何体的主视图、俯视图、左视图都是半径相等的圆,则这
个几何体是( )
A. 球体 B. 圆锥 C. 圆柱 D. 正方体
【分析】利用三视图都是圆,则可得出几何体的形状.
【详解】主视图、俯视图和左视图都是圆的几何体是球,
故选
【点睛】本题考查了由三视图确定几何体的形状,熟悉常见几何体的
三视图是解题的关键.
√
5. 下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形与轴对称图形的定义依次对各项进行分析
即可得到最后结果.
√
【详解】解:A、此图形沿一条直线对折后能够完全重合,此图形是
轴对称图形,但不是中心对称图形,故此选项错误;
B、此图形沿一条直线对折后能够完全重合,此图形是轴对称图形,但
不是中心对称图形,故此选项错误;
C、此图形沿一条直线对折后不能够完全重合,此图形不是轴对称图
形,故此选项错误;
D、此图形沿一条直线对折后能够完全重合,此图形是轴对称图形,
旋转能够与原图形重合,是中心对称图形,故此选项正确.
故选:D.
【点睛】本题主要考查了中心对称图形与轴对称图形的概念,熟练掌
握如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫
做轴对称图形,这条直线叫做对称轴,如果一个图形绕某一点旋转
后能够与自身重合,那么这个图形就叫做中心对称图形,这个点
叫做对称中心,是解答本题的关键.
6. 若关于的一元二次方程有两个不相等的实数根,
则实数的取值范围是( )
A. B.
C. 且 D. 且
【分析】本题考查了根的判别式:一元二次方程
的根与有如下关系:当时,
方程有两个不相等的实数根;当时,方程有两个相等的实数根;
当时,方程无实数根.根据一元二次方程的定义和判别式的意义得
到且,然后求出两不等式的公共部分即可.
√
【详解】解:根据题意得且,
解得且
故选:
7. 十二边形的内角和为( )
A. B. C. D.
【分析】本题考查多边形的内角和定理,根据边形的内角和为
计算即可即可得到答案;
【详解】解:由题意可得,
,
故选:
√
8. 下列计算正确的是( )
A. B.
C. D.
【分析】本题考查同底数幂的乘法,除法及合并同类项,根据
,,,
求解即可得到答案;
√
【详解】解:由题意可得,
,故A不正确,不符合题意,
,故B不正确,不符合题意,
,故C正确,符合题意,
,故D不正确,不符合题意,
故选:
9. 一次空气污染指数抽查中,收集到9天的数据如下:60,70,70,56,81,
91,92,91,75.该组数据的中位数是( )
A. 70 B. 81 C. 91 D. 75
【分析】本题考查了确定一组数据的中位数的能力.注意找中位数的时
候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果
数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两
位数的平均数.找中位数要把数据按从小到大的顺序排列,位于最中间
的一个数(或两个数的平均数)为中位数.
√
【详解】解:将这组数据重新排序为:56、60、70、70、75、81、91、
91、92,
则其中位数为75,
故选:
10. 已知为两个连续整数,且,则等于( )
A. 5 B. 7 C. 9 D. 11
【分析】本题考查了无理数的估算,代数式求值,先估算出的取值
范围,得出的大小,代入求值即可.
【详解】解:,
,
为两个连续整数,且,
,,
,
故选:
√
11. 某商品经过两次连续降价,每件售价由原来的100元降到了81元.设
平均每次降价的百分率为,则下列方程中正确的是( )
A. B.
C. D.
【分析】设平均每次降价的百分率为,可先表示出第一次降价后的价
格,那么第一次降价后的价格降价的百分率,把相应数
值代入即可求解.根据题意列出一元二次方程即可;
√
【详解】解:设平均每次降价的百分率为,根据题意,第一降价后的价
格为,第二次降价后的价格为,即:
故选C
【点睛】本题考查了一元二次方程的应用,理解题意列出方程是解题
的关键.
12. 按一定规律排列的单项式:,,,,,,,
第个单项式是( )
A. B. C. D.
【分析】先分析前面所给出的单项式,从三方面(符号、系数的绝对值、
指数)总结规律,发现规律进行概括即可得到答案.
【详解】解: ,,,,,,,
可记为:
第项为:
故选
√
【点睛】本题考查了单项式的知识,分别找出单项式的系数和次数的
规律是解决此类问题的关键.
13. 对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2
分,3分,
4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据
图中信息,这些学生的平均分数
是【 】( )
A. 2.25 B. 2.5 C. 2.95 D. 3
√
【详解】扇形统计图,条形统计图,频数、频率和总量的关系,加权
平均数.
由得4分的频数12,频率,得总量
由得3分的频率,得频数
由得1 分的频数3,得频率
得2分的频率为
这些学生的平均分数是:
故选
14. 已知都在反比例函数的图
象上,则的关系是( )
A. B. C. D.
【分析】本题考查了反比例函数 性质,根据反比例函数的性质先得
到当时,函数值的大小,然后跟时函数值的大小作比较即可,
掌握反比例函数的性质是解题的关键.
√
【详解】解:反比例函数,
当时,随的增大而减小,当时随的增大而减小,
,
,
,
,
即,
故选:
15. 如图,四边形内接于,的半径为
4,,则的长是( )
A. B. C. D.
【分析】本题考查圆内解四边形对角互补及扇形弧
长公式,根据得到,从而得到,
结合求解即可得到答案;
√
【详解】解:四边形内接于,
,
,
,
,
故选:
二、填空题
16. 使有意义的的取值范围为____________.
/
【分析】本题考查了二次根式有意义 条件:二次根式中的被开方数
必须是非负数,否则二次根式无意义.根据被开方数大于等于0列式计
算即可得解.
【详解】解:有意义,
,
解得:,
故答案为:
17. 分解因式:______________________________.
/
【分析】本题考查因式分解,先提取公因式,再根据平方差公式分解
即可得到答案;
【详解】解:,
故答案为:
18. 如图,在中,点D、E分别是、
边的中点,则______.
/0 5
【分析】根据三角形中位线的性质即可解答.
【详解】点D、E分别是、边的中点
故答案为:
【点睛】本题考查了三角形中位线的性质,熟练掌握上述知识点是解
答本题的关键.
19. 已知圆锥的母线长是10,侧面积是,则此圆锥的高是___.
8
【分析】本题考查了圆锥的计算,一元一次方程的应用,勾股定理,
设圆锥的底面半径为,根据侧面积公式列方程求出半径,再根据勾
股定理进行求解即可.
【详解】解:设圆锥的底面半径为,
则,
解得:,
圆锥的高,
故答案为:8.
三、解答题
20. 计算:
【答案】8
【分析】本题考查了二次根式的混合远算、绝对值化简、负整数指数
幂、特殊角的三角函数等知识,分别根据二次根式的乘法、绝对值、
负整数指数幂,特殊角三角函数等知识化简,再进行计算即可求解.
【详解】解:
21. 如图,点、在线段上,
,,且 求证:
【答案】见解析
【分析】本题主要考查了全等三角形的判定与性质,平行线的性质,
解题的关键是掌握全等三角形的判定与性质.根据可得
,由,推出,结合已知可证明
,最后根据全等三角形的性质即可求解.
【详解】证明:,
,
,
,
即,
,
在和中,
,
,
22. 某城市出租车起步价行驶的最远路程为3千米,超过3千米的部分按
每千米另收费,甲说:“我乘这种出租车走了5千米,付了9元”;乙说:
“我乘这种出租车走了7千米,付了12元”.请你算一算这种出租车的起步
价是多少元?以及超过3千米后,每千米的车费是多少元?
【答案】这种出租车的起步价是6元,超过3千米后,每千米的车费是1.
5元.
【分析】本题考查了二元一次方程组的应用,找准等量关系,正确列
出二元一次方程组是解题的关键.
设这种出租车的起步价是元,超过3千米后,每千米的车费是元,根
据题中的等量关系即可列出二元一次方程组,
【详解】解:设这种出租车的起步价是元,超过3千米后,每千米的
车费是元,
由题意得:,
解得:,
答:这种出租车的起步价是6元,超过3千米后,每千米的车费是1.5元.
23. 某单位决定从甲、乙、丙、丁四名员工中选取两人到社区当志愿者.
现将四名员工的名字分别写在四张完全相同且不透明卡片的正面,把
四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片记
下名字,再从剩余的三张卡片中随机抽取一张卡片,记下名字.
(1)从四张卡片中随机抽取一张,恰好是甲员工的概率为______;
利用概率公式求解即可;
【详解】解:从四张卡片中随机抽取一张,恰好是甲员工的概率为;
第一次 第二次 甲 乙 丙 丁
甲 (乙,甲) (丙,甲) (丁,甲)
乙 (甲,乙) (丙,乙) (丁,乙)
丙 (甲,丙) (乙,丙) (丁,丙)
丁 (甲,丁) (乙,丁) (丙,丁)
共有12个等可能的结果,其中抽签活动中A,B两名志愿者被同时选中
的有2种结果,所以抽签活动中甲、乙两名员工同时被抽中的概率为
答:甲、乙两名员工同时被抽中的概率
(2)请用列表或画树状图的方法,求出甲、乙两名员工同时被抽中的概率.
画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据
概率公式求解即可.
【分析】本题考查的是用列表法或画树状图法求概率.列表法或画树状
图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事
件;树状图法适合两步或两步以上完成的事件;注意概率所求情况
数与总情况数之比.
24. 新能源汽车有着动力强油耗低的特点正逐渐成为人们喜爱的交通工
具.某汽车4S店决定采购新能源甲型和乙型两款汽车,已知每辆甲型汽
车的进价是每辆乙型汽车的进价的倍,若用1800万元购进甲型汽车
的数量比1400万元购进乙型汽车的数量多10辆.
(1)甲型和乙型汽车的进价分别为每辆多少万元?
【答案】甲型汽车的进价为每辆12万元,乙型汽车的进价为每辆10万元;
设乙型汽车的进价为每辆万元,则甲型汽车的进价为每辆万元,
再利用用1800万元购进甲型汽车的数量比1400万元购进乙型汽车的数
量多10辆,再建立方程求解即可;
【详解】解:设乙型汽车的进价为每辆万元,则甲型汽车的进价为每
辆万元,
依题意得:,
解得:,
经检验,是方程的解,,
答:甲型汽车的进价为每辆12万元,乙型汽车的进价为每辆10万元;
(2)该公司决定用不多于1120万元购进甲型和乙型汽车共100辆,最多可
以购买多少辆甲型汽车?
【答案】最多可以购买60辆甲型汽车.
设购买辆甲型汽车,则购买辆乙型汽车,利用公司决定用
不多于1120万元购进甲型和乙型汽车共100辆,再建立不等式解题即可.
【详解】解:设购买辆甲型汽车,则购买辆乙型汽车,
依题意得:
解得:,
答:最多可以购买60辆甲型汽车.
【分析】本题考查的是分式方程的应用,一元一次不等式的应用,理
解题意,确定相等关系与不等关系是解本题的关键;
25. 如图,在矩形中,的垂直平分线分
别交于,连接
(1)求证:四边形是菱形;
【答案】详见解析
先证明四边形是平行四边形,再证明,从而可得结论;
【详解】证明:四边形是矩形,是的中点,
,
,
又,
在和中,
,
,且
四边形是平行四边形,
垂直平分
四边形是菱形;
(2)若,求四边形的面积.
【答案】5
利用菱形的性质与勾股定理求解,再求解面积即可.
【详解】四边形是菱形
,
在中,,
,
四边形的面积
【分析】本题考查的是矩形的性质,菱形的判定与性质,熟练的证明
四边形是菱形是解本题的关键;
26. 在平面直角坐标系中,如果点的横坐标和纵坐标相等,则称点
为和谐点,例如:点,,都是和谐点.
(1)判断函数 图象上是否存在和谐点,若存在,求出其和
谐点的坐标;
【答案】
【详解】解:点的横坐标和纵坐标相等,则称点为和谐点,
和谐点都在上,,
解得,
图象上的和谐点为;
(2)若二次函数的图象上有且只有一个和谐点
当时,函数的最小值为
,最大值为0,求实数的取值范围.
【答案】
【详解】解:二次函数的图象上有且只有一
个和谐点,
,即有两个相等的实数根,
,
解得①,
将代入得,
②,
联立①②,得,,
,
其顶点坐标为,则最小值为,
根据对称轴可知,当时,,
根据函数图象可知,当时,函数的最小
值为,最大值为0,
实数的取值范围为
【分析】本题考查二次函数与一次函数的关系,一次函数与一次函数
交点问题:
(1)根据和谐点定义得到点在上,联合求解即可得到答
案;
(2)根据和谐点联立二次函数与一次函数求解即可得到答案;
27. 如图,是的直径,点是劣弧
上一点,,且平
分与交于点
(1)求证:是的切线;
【答案】详见解析
【分析】根据是的直径,可得,即
,根据同弧所对的圆周角相等,以及已知条件可
得,等量代换后即可得,进而得证;
【详解】证明:是的直径,
,
,
,
,
,
,
,
即,
又是的直径
是的切线;
(2)若,求的长;
【答案】
【分析】连接,根据角平分线的定义,以及等边对等角可得
,根据同弧所对的圆周角相等可得,由垂径定
理可得,进而可得,即可求解.
【详解】如图,连接,
平分,
,
是的直径,
,
即,
,
,
,
;
(3)延长交于点,若,求的半径.
【答案】的半径为
【分析】过点作,根据平行线分线段成比例,求得,
设的半径为,则,证明,可得
,在中,,勾股定理建立方程,
解方程即可求解.
【详解】如图,过点作,交于
..
,
,
平分,
,
,
,
,
,
设 半径为,则,
,
,
,
,
,
,
,
在中,
,
在中,,
即,
解得: (负值舍去),
的半径为
【点睛】本题考查了切线的判定,圆周角定理的推论,平行线分线段
成比例,相似三角形的性质与判定,解直角三角形,综合运用以上知
识是解题的关键.
同课章节目录
