物理人教版(2019)选择性必修第三册2.2气体的等温变化(共36张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第三册2.2气体的等温变化(共36张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 62.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
第二节
气体的等温变化
第二章 气体、固体和气体
学习目标
1
新课讲解
3
新课导入
2
经典例题
4
课堂练习
5
本课小结
6
目录
学习目标
1.通过实验知道气体的等温变化。
2.了解玻意耳定律,能用气体等温变化规律求解简单的实际问题。
新课导入
快要热炸了
为什么图中的轮胎快要热炸了?
温度升高,气体膨胀,压强增大
第一节
气体等温变化的规律
气体等温变化的规律
等温变化
等温变化实验
气体在温度不变的状态下,发生的变化
一定质量的气体,在温度不变的条件下,其压强与体积变化时的关系。
实验目的:
先选定一个热力学系统,比如一定质量的空气,在温度不变的情况下,测量气体在不同体积时的压强,再分析气体压强与体积的关系。
实验原理:
等温变化实验
等温变化实验
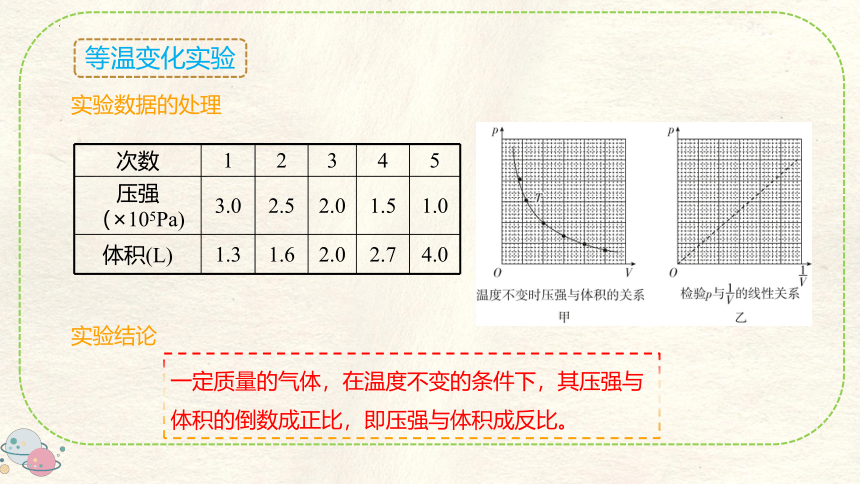
实验数据的处理
次数 1 2 3 4 5
压强(×105Pa) 3.0 2.5 2.0 1.5 1.0
体积(L) 1.3 1.6 2.0 2.7 4.0
一定质量的气体,在温度不变的条件下,其压强与体积的倒数成正比,即压强与体积成反比。
实验结论
状态参量与平衡态
状态参量
描述物质系统状态的宏观物理量叫做状态参量
系统间力的作用用压强P
力学参量
几何参量
确定系统冷热程度用温度T
热学参量
容积为100L
温度为20oC
确定空间范围用体积V
状态参量
第二节
玻意耳定律
玻意耳定律
玻意耳定律
1.内容
一定质量的某种气体,在 不变的情况下,压强p与体积V成 。
2.公式
pV=C或 。
3.条件
气体的 一定, 不变。
4.适用范围:温度不太低,压强不太大。
p1V1=p2V2
反比
质量
温度
温度
玻意耳定律
等温线
P
1/V
P
V
图像:
物理意义:反映压强随体积的变化关系。
玻意耳定律
两种等温变化图像所比较
p
V
0
t1
t2
离原点越远,温度越高
T2>T1
斜率越大,温度越高
玻意耳定律的理解及应用
(1)玻意耳定律成立的条件是什么?
答案 一定质量的气体,且温度不变
(2)用p1V1=p2V2解题时各物理量的单位必须是国际单位制中的单位吗?
答案 不必.只要同一物理量使用同一单位即可
(3)玻意耳定律的表达式pV=C中的C是一个与气体无关的常量吗?
答案 pV=C中的常量C不是一个普适恒量,它与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量越大.
玻意耳定律的理解及应用
1.常量的意义
p1V1=p2V2=C,该常量C与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量C越大.
2.应用玻意耳定律解题的一般步骤
(1)确定研究对象,并判断是否满足玻意耳定律的条件.
(2)确定初、末状态及状态参量(p1、V1;p2、V2).
(3)根据玻意耳定律列方程求解.(注意统一单位)
(4)注意分析隐含条件,作出必要的判断和说明.
特别提醒 确定气体压强或体积时,只要初、末状态的单位统一即可,没有必要都转换成国际单位制.
第三节
封闭气体压强的计算
封闭气体压强的计算
h
A
B
h
D
C
p=p0+ρgh
p=p0-ρgh
p = p0-ρgh
h
①取等压面法:同一水平液面处压强相同
容器静止或匀速运动时封闭气体压强的计算
封闭气体压强的计算
②力平衡法
汽缸横截面积为S,活塞质量为m
h
h
h
m
M
m
S
S
m
封闭气体压强的计算
当容器加速运动时,通常选与气体相关联的液柱、汽缸或活塞为研究对象,并对其进行受力分析,然后由牛顿第二定律列方程,求出封闭气体的压强。
容器加速时封闭气体压强的计算
如图所示,当竖直放置的玻璃管向上加速运动时,对液柱受力分析有:
pS-p0S-mg=ma
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
求用固体(如活塞)封闭在静止容器内的气体压强,应对固体进行受力分析。然后根据平衡条件求解。
G
P0S
PS
PS = P0S+mg
m
S
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
S
m
G
PS
P0S′
S′
PS =mg +P0S'cosθ
PS = mg+P0S
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
M
m
S
M
m
S
以活塞为研究对象
以气缸为研究对象
mg+PS = P0S
Mg+PS = P0S
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
1. 理论依据
(1)液体压强的计算公式 p = gh。
(2)液面与外界大气相接触,则液面下h处的压强为 p = p0 + gh
(3)连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平面上的压强是相等的。
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
(1)连通器原理:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面.由两侧压强相等列方程求解压强。
例如图中,同一液面C、D处压强相等 pA=p0+ph。
2.计算方法
(2)受力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强。
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
2.计算方法
(3)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强。
例如,图中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知 (pA+ph0)S=(p0+ph+ph0)S。即pA=p0+ph。
封闭气体压强的计算
①
h
h
②
h
③
下列各图装置均处于静止状态。设大气压强为P0,用水银(或活塞)封闭一定量的气体在玻璃管(或气缸)中,求封闭气体的压强P
P =ρgh
P = cmHg(柱)
P—帕
h—米
P =P0
P =P0+ρgh
P =P0- ρgh
封闭气体压强的计算
h
④
h
⑤
h
⑥
连通器原理:同种液体在同一高度压强相等
P =P0+ρgh
P =P0- ρgh
P =P0- ρgh
经典例题
如图所示,竖直静止放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内.已知水银柱a长h1为10 cm,水银柱b两个液面间的高度差h2为5 cm,大气压强为75 cmHg,求空气柱A、B的压强分别是多少.
65 cmHg 60 cmHg
答案:65 cmHg 60 cmHg
设管的横截面积为S,选a的下端面为参考液面,它受向下的压力为(pA+ph1)S,受向上的大气压力为p0S,由于系统处于静止状态,则
(pA+ph1)S=p0S,
所以pA=p0-ph1=(75-10) cmHg=65 cmHg,
再选b的左下端面为参考液面,由连通器原理知:液柱h2的上表面处的压强等于pB,则(pB+ph2)S=pAS,所以pB=pA-ph2=(65-5) cmHg=60 cmHg.
如图所示,竖直放置的导热汽缸,活塞横截面积为S=0.01 m2,可在汽缸内无摩擦滑动,汽缸侧壁有一个小孔与装有水银的U形玻璃管相通,汽缸内封闭了一段高为H=70 cm的气柱(U形管内的气体体积不计).已知活塞质量m=6.8 kg,大气压强p0=1×105 Pa,水银密度ρ=13.6×103 kg/m3,g=10 m/s2.
(1)求U形管中左管与右管的水银面的高度差h1;
5 cm
答案:5 cm
以活塞为研究对象,p0S+mg=p1S
得
而p1=p0+ρgh1
所以有
解得:
如图所示,竖直放置的导热汽缸,活塞横截面积为S=0.01 m2,可在汽缸内无摩擦滑动,汽缸侧壁有一个小孔与装有水银的U形玻璃管相通,汽缸内封闭了一段高为H=70 cm的气柱(U形管内的气体体积不计).已知活塞质量m=6.8 kg,大气压强p0=1×105 Pa,水银密度ρ=13.6×103 kg/m3,g=10 m/s2.
(2)若在活塞上加一竖直向上的拉力使U形管中左管
水银面高出右管水银面h2=5 cm,求活塞平衡时与汽
缸底部的高度为多少厘米(结果保留整数).
80 cm
答案:80 cm
活塞上加一竖直向上的拉力,U形管中左管水银面高出右管水银面h2=5 cm
封闭气体的压强p2=p0-ρgh2=(1×105-13.6×103×10×0.05) Pa=93 200 Pa
初始时封闭气体的压强为:
汽缸内的气体发生的是等温变化,根据玻意耳定律,有:p1V1=p2V2
代入数据:106 800×70S=93 200×hS
解得:h≈80 cm.
如图所示,一开口向上的汽缸固定在水平地面上,质量均为m、横截面积均为S且厚度不计的活塞A、B将缸内气体分成Ⅰ、Ⅱ两部分.在活塞A的上方放置一质量为2m的物块,整个装置处于平衡状态,此时Ⅰ、Ⅱ两部分气体的长度均为l0.已知大气压强与活塞质量的关系为p0= ,活塞移动过程中无气体泄漏且温度始终保持不变,不计一切摩擦,汽缸足够高.现将活塞A上面的物块取走,
试求重新达到平衡状态后,A活塞上升的高度.
0.9l0
当堂检测
答案:0.9l0
对Ⅰ部分气体,其初态压强 ,末态压强为
解得
对Ⅱ部分气体,其初态压强为
末态压强为
设末态时Ⅱ部分气体的长度为l2,则由玻意耳定律可得p2l0S=p2′l2S
代入数据解得
设末态时Ⅰ部分气体的长度为l1,则由玻意耳定律可得p1l0S=p1′l1S
故活塞A上升的高度为Δh=l1+l2-2l0=0.9l0
本课小结
气体的等温变化
探究气体等温变化的规律
玻意耳定律
平衡态下固体(活塞、气缸)密闭气体压强的计算
等温变化实验
一定质量的气体,在温度不变的情况下,它的压强P跟体积V成反比。
表达式PV=C
P1V1=P2V2
适用条件
图像
平衡态下液体封闭气体压强的计算
第二节
气体的等温变化
第二章 气体、固体和气体
学习目标
1
新课讲解
3
新课导入
2
经典例题
4
课堂练习
5
本课小结
6
目录
学习目标
1.通过实验知道气体的等温变化。
2.了解玻意耳定律,能用气体等温变化规律求解简单的实际问题。
新课导入
快要热炸了
为什么图中的轮胎快要热炸了?
温度升高,气体膨胀,压强增大
第一节
气体等温变化的规律
气体等温变化的规律
等温变化
等温变化实验
气体在温度不变的状态下,发生的变化
一定质量的气体,在温度不变的条件下,其压强与体积变化时的关系。
实验目的:
先选定一个热力学系统,比如一定质量的空气,在温度不变的情况下,测量气体在不同体积时的压强,再分析气体压强与体积的关系。
实验原理:
等温变化实验
等温变化实验
实验数据的处理
次数 1 2 3 4 5
压强(×105Pa) 3.0 2.5 2.0 1.5 1.0
体积(L) 1.3 1.6 2.0 2.7 4.0
一定质量的气体,在温度不变的条件下,其压强与体积的倒数成正比,即压强与体积成反比。
实验结论
状态参量与平衡态
状态参量
描述物质系统状态的宏观物理量叫做状态参量
系统间力的作用用压强P
力学参量
几何参量
确定系统冷热程度用温度T
热学参量
容积为100L
温度为20oC
确定空间范围用体积V
状态参量
第二节
玻意耳定律
玻意耳定律
玻意耳定律
1.内容
一定质量的某种气体,在 不变的情况下,压强p与体积V成 。
2.公式
pV=C或 。
3.条件
气体的 一定, 不变。
4.适用范围:温度不太低,压强不太大。
p1V1=p2V2
反比
质量
温度
温度
玻意耳定律
等温线
P
1/V
P
V
图像:
物理意义:反映压强随体积的变化关系。
玻意耳定律
两种等温变化图像所比较
p
V
0
t1
t2
离原点越远,温度越高
T2>T1
斜率越大,温度越高
玻意耳定律的理解及应用
(1)玻意耳定律成立的条件是什么?
答案 一定质量的气体,且温度不变
(2)用p1V1=p2V2解题时各物理量的单位必须是国际单位制中的单位吗?
答案 不必.只要同一物理量使用同一单位即可
(3)玻意耳定律的表达式pV=C中的C是一个与气体无关的常量吗?
答案 pV=C中的常量C不是一个普适恒量,它与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量越大.
玻意耳定律的理解及应用
1.常量的意义
p1V1=p2V2=C,该常量C与气体的种类、质量、温度有关,对一定质量的气体,温度越高,该常量C越大.
2.应用玻意耳定律解题的一般步骤
(1)确定研究对象,并判断是否满足玻意耳定律的条件.
(2)确定初、末状态及状态参量(p1、V1;p2、V2).
(3)根据玻意耳定律列方程求解.(注意统一单位)
(4)注意分析隐含条件,作出必要的判断和说明.
特别提醒 确定气体压强或体积时,只要初、末状态的单位统一即可,没有必要都转换成国际单位制.
第三节
封闭气体压强的计算
封闭气体压强的计算
h
A
B
h
D
C
p=p0+ρgh
p=p0-ρgh
p = p0-ρgh
h
①取等压面法:同一水平液面处压强相同
容器静止或匀速运动时封闭气体压强的计算
封闭气体压强的计算
②力平衡法
汽缸横截面积为S,活塞质量为m
h
h
h
m
M
m
S
S
m
封闭气体压强的计算
当容器加速运动时,通常选与气体相关联的液柱、汽缸或活塞为研究对象,并对其进行受力分析,然后由牛顿第二定律列方程,求出封闭气体的压强。
容器加速时封闭气体压强的计算
如图所示,当竖直放置的玻璃管向上加速运动时,对液柱受力分析有:
pS-p0S-mg=ma
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
求用固体(如活塞)封闭在静止容器内的气体压强,应对固体进行受力分析。然后根据平衡条件求解。
G
P0S
PS
PS = P0S+mg
m
S
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
S
m
G
PS
P0S′
S′
PS =mg +P0S'cosθ
PS = mg+P0S
封闭气体压强的计算
平衡态下固体(活塞、气缸)密闭气体压强的计算
M
m
S
M
m
S
以活塞为研究对象
以气缸为研究对象
mg+PS = P0S
Mg+PS = P0S
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
1. 理论依据
(1)液体压强的计算公式 p = gh。
(2)液面与外界大气相接触,则液面下h处的压强为 p = p0 + gh
(3)连通器原理:在连通器中,同一种液体(中间液体不间断)的同一水平面上的压强是相等的。
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
(1)连通器原理:根据同种液体在同一水平液面处压强相等,在连通器内灵活选取等压面.由两侧压强相等列方程求解压强。
例如图中,同一液面C、D处压强相等 pA=p0+ph。
2.计算方法
(2)受力平衡法:选与封闭气体接触的液柱为研究对象进行受力分析,由F合=0列式求气体压强。
封闭气体压强的计算
平衡态下液体密闭气体压强的计算
2.计算方法
(3)参考液片法:选取假想的液体薄片(自身重力不计)为研究对象,分析液片两侧受力情况,建立平衡方程消去面积,得到液片两侧压强相等,进而求得气体压强。
例如,图中粗细均匀的U形管中封闭了一定质量的气体A,在其最低处取一液片B,由其两侧受力平衡可知 (pA+ph0)S=(p0+ph+ph0)S。即pA=p0+ph。
封闭气体压强的计算
①
h
h
②
h
③
下列各图装置均处于静止状态。设大气压强为P0,用水银(或活塞)封闭一定量的气体在玻璃管(或气缸)中,求封闭气体的压强P
P =ρgh
P = cmHg(柱)
P—帕
h—米
P =P0
P =P0+ρgh
P =P0- ρgh
封闭气体压强的计算
h
④
h
⑤
h
⑥
连通器原理:同种液体在同一高度压强相等
P =P0+ρgh
P =P0- ρgh
P =P0- ρgh
经典例题
如图所示,竖直静止放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内.已知水银柱a长h1为10 cm,水银柱b两个液面间的高度差h2为5 cm,大气压强为75 cmHg,求空气柱A、B的压强分别是多少.
65 cmHg 60 cmHg
答案:65 cmHg 60 cmHg
设管的横截面积为S,选a的下端面为参考液面,它受向下的压力为(pA+ph1)S,受向上的大气压力为p0S,由于系统处于静止状态,则
(pA+ph1)S=p0S,
所以pA=p0-ph1=(75-10) cmHg=65 cmHg,
再选b的左下端面为参考液面,由连通器原理知:液柱h2的上表面处的压强等于pB,则(pB+ph2)S=pAS,所以pB=pA-ph2=(65-5) cmHg=60 cmHg.
如图所示,竖直放置的导热汽缸,活塞横截面积为S=0.01 m2,可在汽缸内无摩擦滑动,汽缸侧壁有一个小孔与装有水银的U形玻璃管相通,汽缸内封闭了一段高为H=70 cm的气柱(U形管内的气体体积不计).已知活塞质量m=6.8 kg,大气压强p0=1×105 Pa,水银密度ρ=13.6×103 kg/m3,g=10 m/s2.
(1)求U形管中左管与右管的水银面的高度差h1;
5 cm
答案:5 cm
以活塞为研究对象,p0S+mg=p1S
得
而p1=p0+ρgh1
所以有
解得:
如图所示,竖直放置的导热汽缸,活塞横截面积为S=0.01 m2,可在汽缸内无摩擦滑动,汽缸侧壁有一个小孔与装有水银的U形玻璃管相通,汽缸内封闭了一段高为H=70 cm的气柱(U形管内的气体体积不计).已知活塞质量m=6.8 kg,大气压强p0=1×105 Pa,水银密度ρ=13.6×103 kg/m3,g=10 m/s2.
(2)若在活塞上加一竖直向上的拉力使U形管中左管
水银面高出右管水银面h2=5 cm,求活塞平衡时与汽
缸底部的高度为多少厘米(结果保留整数).
80 cm
答案:80 cm
活塞上加一竖直向上的拉力,U形管中左管水银面高出右管水银面h2=5 cm
封闭气体的压强p2=p0-ρgh2=(1×105-13.6×103×10×0.05) Pa=93 200 Pa
初始时封闭气体的压强为:
汽缸内的气体发生的是等温变化,根据玻意耳定律,有:p1V1=p2V2
代入数据:106 800×70S=93 200×hS
解得:h≈80 cm.
如图所示,一开口向上的汽缸固定在水平地面上,质量均为m、横截面积均为S且厚度不计的活塞A、B将缸内气体分成Ⅰ、Ⅱ两部分.在活塞A的上方放置一质量为2m的物块,整个装置处于平衡状态,此时Ⅰ、Ⅱ两部分气体的长度均为l0.已知大气压强与活塞质量的关系为p0= ,活塞移动过程中无气体泄漏且温度始终保持不变,不计一切摩擦,汽缸足够高.现将活塞A上面的物块取走,
试求重新达到平衡状态后,A活塞上升的高度.
0.9l0
当堂检测
答案:0.9l0
对Ⅰ部分气体,其初态压强 ,末态压强为
解得
对Ⅱ部分气体,其初态压强为
末态压强为
设末态时Ⅱ部分气体的长度为l2,则由玻意耳定律可得p2l0S=p2′l2S
代入数据解得
设末态时Ⅰ部分气体的长度为l1,则由玻意耳定律可得p1l0S=p1′l1S
故活塞A上升的高度为Δh=l1+l2-2l0=0.9l0
本课小结
气体的等温变化
探究气体等温变化的规律
玻意耳定律
平衡态下固体(活塞、气缸)密闭气体压强的计算
等温变化实验
一定质量的气体,在温度不变的情况下,它的压强P跟体积V成反比。
表达式PV=C
P1V1=P2V2
适用条件
图像
平衡态下液体封闭气体压强的计算
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
