2023-2024学年冀教版数学九年级下册第二十九章 直线与圆的位置关系专项1 与切线有关的证明与计算 课件-(21张PPT)
文档属性
| 名称 | 2023-2024学年冀教版数学九年级下册第二十九章 直线与圆的位置关系专项1 与切线有关的证明与计算 课件-(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 721.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第二十九章 直线与圆的位置关系
专项1 与切线有关的证明与计算——河北中考热点
过专项 阶段强化专项训练
类型1 连半径,证垂直
模型展示
(1)如图1,已知 是 上一点, 为 的半径,证 ,得 是
的切线.
图1
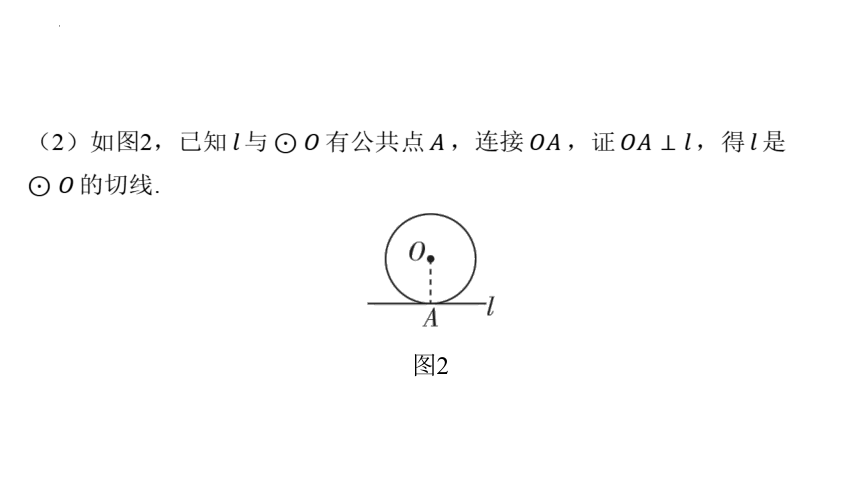
(2)如图2,已知 与 有公共点 ,连接 ,证 ,得 是
的切线.
图2
1.一题多解 [2023沧州期末]如图,已知 ,以 为
圆心、 长为半径的圆交 于 ,交 的延长线于
点 ,过 作 的垂线交 的延长线于 ,连接 ,
且 平分 .
(1)求证: 与 相切于点 .
证明:证法一 如图, 平分 , ,
, ,
, ,
, ,
又 为 的半径,
与 相切于点 .
证法二 如图, 平分 , ,
, ,
.
, ,
,
,
又 为 的半径,
与 相切于点 .
(2)若 , ,求圆的半径.
解:在 中, ,
, ,
又 ,
.
连接 ,如图,在 中, , ,
,
圆的半径为2.
2.[2023十堰中考]如图,在 中,
, ,点 在 上,以
为圆心、 为半径的半圆分别与 ,
, 有公共点 , , ,且点 是
的中点.
(1)求证: 与半圆 相切.
证明:连接 , ,如图,
, ,
,
,
,
,
点 是 的中点,
,
,
.
为半圆 的半径, 与半圆 相切.
(2)若 ,求图中阴影部分的面积(结果保留 ).
解: , ,
为等腰直角三角形,
设 ,则 ,
,
,
,
,
.
3.[2022乐山中考]如图,线段 为 的直
径,点 , 在 上, ,过点
作 ,垂足为点 ,连接 交 于
点 .
(1)求证: .
证明:如图,连接 ,
线段 为 的直径,
, .
,
,
.
, ,
, .
(2)已知 的半径为6, ,延长 至点 ,使 .
求证: 与 相切.
如图,连接 ,交 于 ,
, .
, , .
, .
又 , ,
, .
又 是 的半径, 与 相切.
类型2 作垂直,证半径
模型展示
已知 的半径为 ,过点 作 于点 ,证 ,得 是
的切线.
4.[2023广西中考]如图, 平分 ,
与 相切于点 ,延长 交 于点 ,过
点 作 ,垂足为 .
(1)求证: 与 相切.
证明: 与 相切于点 ,且 是 的半径,
,
平分 , 于点 , 于点 ,
, 点 在 上,
是 的半径,且 ,
与 相切.
(2)若 的半径为4, ,求 的长.
解: , ,
,
, ,
.
, ,
,
的长是12.
第二十九章 直线与圆的位置关系
专项1 与切线有关的证明与计算——河北中考热点
过专项 阶段强化专项训练
类型1 连半径,证垂直
模型展示
(1)如图1,已知 是 上一点, 为 的半径,证 ,得 是
的切线.
图1
(2)如图2,已知 与 有公共点 ,连接 ,证 ,得 是
的切线.
图2
1.一题多解 [2023沧州期末]如图,已知 ,以 为
圆心、 长为半径的圆交 于 ,交 的延长线于
点 ,过 作 的垂线交 的延长线于 ,连接 ,
且 平分 .
(1)求证: 与 相切于点 .
证明:证法一 如图, 平分 , ,
, ,
, ,
, ,
又 为 的半径,
与 相切于点 .
证法二 如图, 平分 , ,
, ,
.
, ,
,
,
又 为 的半径,
与 相切于点 .
(2)若 , ,求圆的半径.
解:在 中, ,
, ,
又 ,
.
连接 ,如图,在 中, , ,
,
圆的半径为2.
2.[2023十堰中考]如图,在 中,
, ,点 在 上,以
为圆心、 为半径的半圆分别与 ,
, 有公共点 , , ,且点 是
的中点.
(1)求证: 与半圆 相切.
证明:连接 , ,如图,
, ,
,
,
,
,
点 是 的中点,
,
,
.
为半圆 的半径, 与半圆 相切.
(2)若 ,求图中阴影部分的面积(结果保留 ).
解: , ,
为等腰直角三角形,
设 ,则 ,
,
,
,
,
.
3.[2022乐山中考]如图,线段 为 的直
径,点 , 在 上, ,过点
作 ,垂足为点 ,连接 交 于
点 .
(1)求证: .
证明:如图,连接 ,
线段 为 的直径,
, .
,
,
.
, ,
, .
(2)已知 的半径为6, ,延长 至点 ,使 .
求证: 与 相切.
如图,连接 ,交 于 ,
, .
, , .
, .
又 , ,
, .
又 是 的半径, 与 相切.
类型2 作垂直,证半径
模型展示
已知 的半径为 ,过点 作 于点 ,证 ,得 是
的切线.
4.[2023广西中考]如图, 平分 ,
与 相切于点 ,延长 交 于点 ,过
点 作 ,垂足为 .
(1)求证: 与 相切.
证明: 与 相切于点 ,且 是 的半径,
,
平分 , 于点 , 于点 ,
, 点 在 上,
是 的半径,且 ,
与 相切.
(2)若 的半径为4, ,求 的长.
解: , ,
,
, ,
.
, ,
,
的长是12.
