人教版第二十章数据的分析章末复习 课件-2023-2024学年人教版数学八年级下册(28张PPT)
文档属性
| 名称 | 人教版第二十章数据的分析章末复习 课件-2023-2024学年人教版数学八年级下册(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 23:02:31 | ||
图片预览





文档简介
(共28张PPT)
第二十章数据的分析章末复习
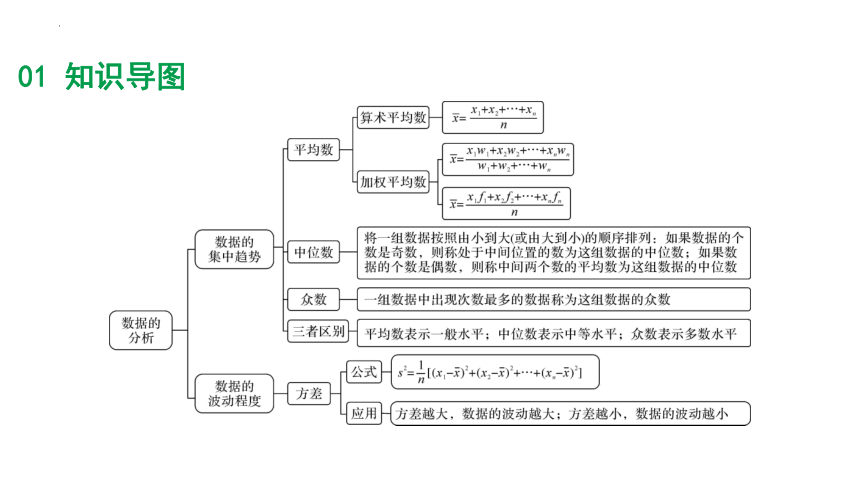
01 知识导图
02 聚焦广东
考点1 平均数、中位数、众数和方差的计算
1.(1)(2023·中山期末)数据3,4,4,5,7的众数是___.
(2)(2023·广州海珠区期末)一组数据1,6,7,4,7,5,2的中
位数是___.
(3)(2022·广州荔湾区期末改编)已知一组数据2, ,6,9,12的平均
数为7,则 ____,该组数据的方差为_ __.
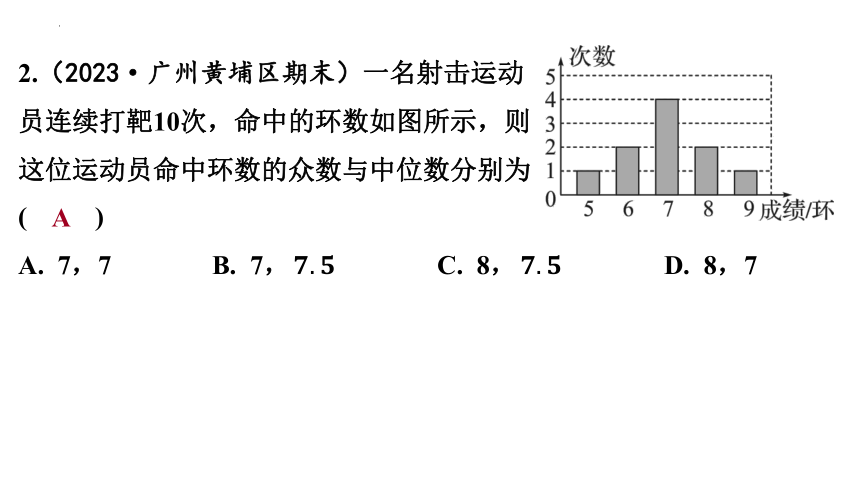
2.(2023·广州黄埔区期末)一名射击运动
员连续打靶10次,命中的环数如图所示,则
这位运动员命中环数的众数与中位数分别为
( )
A
A. 7,7 B. 7, C. 8, D. 8,7
3.(2023·惠州惠东县期末)21世纪已经进入了中国太空时代,2021
年到2022年,我国通过11次航天发射完成空间站建设,空间站由“天和”
核心舱、“问天”和“梦天”两个实验舱,我国空间站的建成将为开展太
空实验及更广泛的国际合作提供精彩舞台.校团委以此为契机,组织了
“中国梦·航天情”系列活动.下面是八年级甲、乙两个班各项目的成绩
(单位:分)
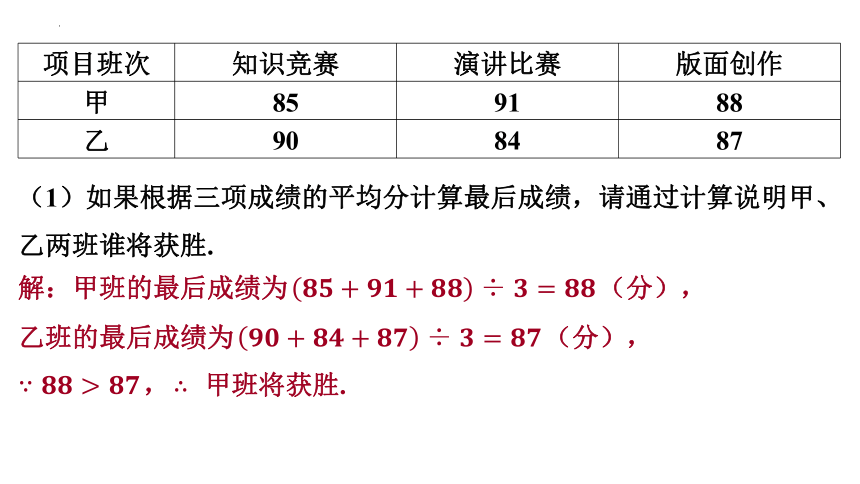
项目班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
(1)如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲、乙两班谁将获胜.
解:甲班的最后成绩为 (分),
乙班的最后成绩为 (分),
, 甲班将获胜.
(2)如果将知识竞赛、演讲比赛、版面创作按 的比例确定最后
成绩,请通过计算说明甲乙两班谁将获胜.
[答案] 由题意可得,甲班的最后成绩为 (分),
乙班的最后成绩为 (分),
, 乙班将获胜.
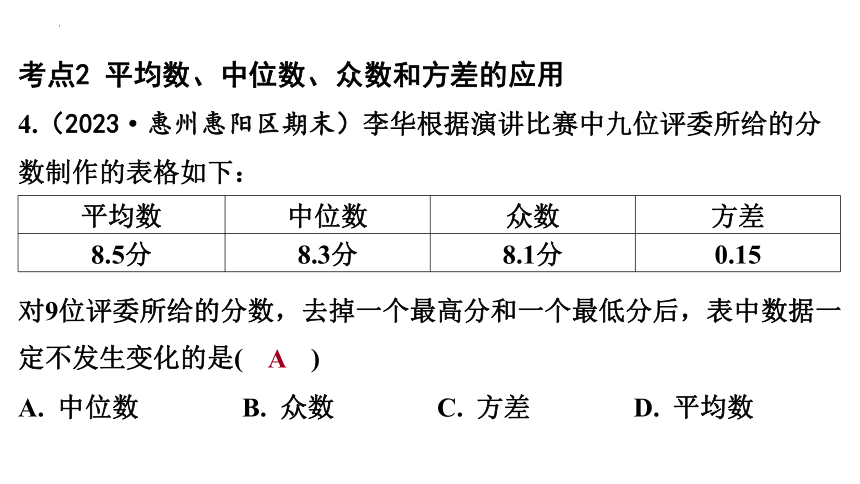
考点2 平均数、中位数、众数和方差的应用
4.(2023·惠州惠阳区期末)李华根据演讲比赛中九位评委所给的分数制作的表格如下:
平均数 中位数 众数 方差
8.5分 8.3分 8.1分 0.15
对9位评委所给的分数,去掉一个最高分和一个最低分后,表中数据一
定不发生变化的是( )
A
A. 中位数 B. 众数 C. 方差 D. 平均数
5.(2023·珠海香洲区期末)甲、乙、丙三个旅行团的游客人数相等,
且平均年龄都是32岁,游客年龄的方差分别是 ,
, .导游小王最喜欢带游客年龄相近的旅行团,则
他应选( )
C
A. 甲旅行团 B. 乙旅行团 C. 丙旅行团 D. 无法确定
6.(2023·广东)小红家到学校有两条公共汽车线路.为了解两条线路
的乘车所用时间,小红做了试验,第一周(5个工作日)选择 线路,
第二周(5个工作日)选择 线路,每天在固定时间段内乘车2次并分
别记录所用时间.数据(单位: )统计如下:
实验序号 1 2 3 4 5 6 7 8 9 10
线路所用时间/ 15 32 15 16 34 18 21 14 35 20
线路所用时间/ 25 29 23 25 27 26 31 28 30 24
统计量 平均数 中位数 众数 方差
线路所用时间/ 22 15 63.2
线路所用时间/ 26.5 6.36
根据以上信息解答下列问题:
(1)填空: ____, _____, ____.
19
26.8
25
续表
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
解:小红统计的选择 线路的平均数为22,选
择 线路的平均数为 ,用时差不太多.而
方差 ,因此 路线的波动性更小.
所以选择 路线更优.
课后强化
1.(2023·巴中)一组数据1,3,5,2,8,13的中位数是___.
4
2.(2023·营口)某班35名同学一周课外阅读时间统计如表所示:
时间/时 7 8 9 10
人数/人 4 12 13 6
则该班35名同学一周课外阅读时间的众数是___小时.
9
3.(2022·东莞期末)小丽的笔试成绩为100分,面试成绩为90分.若得
笔试成绩、面试成绩按 的比例计算平均成绩,则小丽的平均成绩
是 ____分.
96
4.(2023·广州黄埔区期末)在一次芭蕾舞比赛中,甲、乙两个芭蕾
舞团参加表演的女演员的身高的方差分别是 , ,则
____(填“甲”或“乙” )芭蕾舞团演员的身高更整齐.
甲
5.(2023·泰安)为了解学生的身体素质状况,国家每年都会进行中
小学生身体素质抽测.在今年的抽测中,某校九年级二班随机抽取了10
名男生进行引体向上测试,他们的成绩(单位:个)如下:7,11,10,
11,6,14,11,10,11,9.根据这组数据判断下列结论中错误的是
( )
B
A. 这组数据的众数是11 B. 这组数据的中位数是10
C. 这组数据的平均数是10 D. 这组数据的方差是4.6
6.(2023·珠海斗门区期末)为了解养殖鱼的生长情况,养鱼者从鱼塘中随机捕捞了20条鱼,称得它们的质量如下表:
质量/ 1.0 1.2 1.5 2
频数 4 5 8 3
(1)样本的中位数是 ____.
1.5
(2)如果鱼塘里有10 000条鱼,通过计算估计鱼塘共有多少千克的鱼.
解: ,
.
答:鱼塘大约共有14 000千克的鱼.
7.(2023·惠州惠城区期末)在“我的中国梦”演讲比赛中,有5名学生
参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自
己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩
的( )
A
A. 中位数 B. 众数 C. 平均数 D. 方差
8.(2023·惠州惠城区期末)惠城区横沥
镇的陈大叔承包了甲、乙两座小山,各栽
了100棵荔枝树,发现其成活率均为 ,
为了分析收成情况,他分别从两山上各随
(1)直接写出甲山的4棵荔枝树的产量的中位数.
解: .
机采摘了4棵树的荔枝,每棵的产量如折线统计图所示.
(2)分别计算甲、乙两座山的荔枝样本的平均数,并判断哪座山的样本的产量高.
[答案] (千克), (千克),
甲、乙两山的样本的产量一样多.
(3)用样本平均数估计甲、乙两座山的荔枝的产量总和.
[答案] 总产量为 (千克).
答:甲、乙两山荔枝的产量总和为7 760千克.
9.(2023·珠海香洲区期末)为普及“垃圾分类”知识,某校组织全校
学生参加了垃圾分类主题知识竞赛.为了解竞赛成绩,学校随机抽样调
查了七、八年级各10名学生的成绩 (单位:分),分数如下:
七年级10名学生竞赛成绩:92,83,99,89,99,86,100,81,92,
99;
八年级10名学生竞赛成绩中分布在 的成绩:93,94,95.
【整理数据】:
年级
七年级 2 2 4
八年级 1 2 3 4
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 92 45.8
八年级 94 100 38.2
根据以上提供的信息,回答下列问题:
(1)填空: ___, ____, ____, _____.
2
99
92
94.5
(2)若该校七年级学生有300人,且全部参加竞赛,请估计七年级成绩高于90分的人数.
解: (人).
答:七年级成绩高于90分的人数大约为180人.
(3)请你根据以上信息,推断哪个年级的成绩更好,并说明理由(写出一条理由即可).
解:八年级成绩更好.理由:
从平均数看,八年级成绩的平均数大于七年级,所以八年级成绩更好.(答案不唯一)
第二十章数据的分析章末复习
01 知识导图
02 聚焦广东
考点1 平均数、中位数、众数和方差的计算
1.(1)(2023·中山期末)数据3,4,4,5,7的众数是___.
(2)(2023·广州海珠区期末)一组数据1,6,7,4,7,5,2的中
位数是___.
(3)(2022·广州荔湾区期末改编)已知一组数据2, ,6,9,12的平均
数为7,则 ____,该组数据的方差为_ __.
2.(2023·广州黄埔区期末)一名射击运动
员连续打靶10次,命中的环数如图所示,则
这位运动员命中环数的众数与中位数分别为
( )
A
A. 7,7 B. 7, C. 8, D. 8,7
3.(2023·惠州惠东县期末)21世纪已经进入了中国太空时代,2021
年到2022年,我国通过11次航天发射完成空间站建设,空间站由“天和”
核心舱、“问天”和“梦天”两个实验舱,我国空间站的建成将为开展太
空实验及更广泛的国际合作提供精彩舞台.校团委以此为契机,组织了
“中国梦·航天情”系列活动.下面是八年级甲、乙两个班各项目的成绩
(单位:分)
项目班次 知识竞赛 演讲比赛 版面创作
甲 85 91 88
乙 90 84 87
(1)如果根据三项成绩的平均分计算最后成绩,请通过计算说明甲、乙两班谁将获胜.
解:甲班的最后成绩为 (分),
乙班的最后成绩为 (分),
, 甲班将获胜.
(2)如果将知识竞赛、演讲比赛、版面创作按 的比例确定最后
成绩,请通过计算说明甲乙两班谁将获胜.
[答案] 由题意可得,甲班的最后成绩为 (分),
乙班的最后成绩为 (分),
, 乙班将获胜.
考点2 平均数、中位数、众数和方差的应用
4.(2023·惠州惠阳区期末)李华根据演讲比赛中九位评委所给的分数制作的表格如下:
平均数 中位数 众数 方差
8.5分 8.3分 8.1分 0.15
对9位评委所给的分数,去掉一个最高分和一个最低分后,表中数据一
定不发生变化的是( )
A
A. 中位数 B. 众数 C. 方差 D. 平均数
5.(2023·珠海香洲区期末)甲、乙、丙三个旅行团的游客人数相等,
且平均年龄都是32岁,游客年龄的方差分别是 ,
, .导游小王最喜欢带游客年龄相近的旅行团,则
他应选( )
C
A. 甲旅行团 B. 乙旅行团 C. 丙旅行团 D. 无法确定
6.(2023·广东)小红家到学校有两条公共汽车线路.为了解两条线路
的乘车所用时间,小红做了试验,第一周(5个工作日)选择 线路,
第二周(5个工作日)选择 线路,每天在固定时间段内乘车2次并分
别记录所用时间.数据(单位: )统计如下:
实验序号 1 2 3 4 5 6 7 8 9 10
线路所用时间/ 15 32 15 16 34 18 21 14 35 20
线路所用时间/ 25 29 23 25 27 26 31 28 30 24
统计量 平均数 中位数 众数 方差
线路所用时间/ 22 15 63.2
线路所用时间/ 26.5 6.36
根据以上信息解答下列问题:
(1)填空: ____, _____, ____.
19
26.8
25
续表
(2)应用你所学的统计知识,帮助小红分析如何选择乘车线路.
解:小红统计的选择 线路的平均数为22,选
择 线路的平均数为 ,用时差不太多.而
方差 ,因此 路线的波动性更小.
所以选择 路线更优.
课后强化
1.(2023·巴中)一组数据1,3,5,2,8,13的中位数是___.
4
2.(2023·营口)某班35名同学一周课外阅读时间统计如表所示:
时间/时 7 8 9 10
人数/人 4 12 13 6
则该班35名同学一周课外阅读时间的众数是___小时.
9
3.(2022·东莞期末)小丽的笔试成绩为100分,面试成绩为90分.若得
笔试成绩、面试成绩按 的比例计算平均成绩,则小丽的平均成绩
是 ____分.
96
4.(2023·广州黄埔区期末)在一次芭蕾舞比赛中,甲、乙两个芭蕾
舞团参加表演的女演员的身高的方差分别是 , ,则
____(填“甲”或“乙” )芭蕾舞团演员的身高更整齐.
甲
5.(2023·泰安)为了解学生的身体素质状况,国家每年都会进行中
小学生身体素质抽测.在今年的抽测中,某校九年级二班随机抽取了10
名男生进行引体向上测试,他们的成绩(单位:个)如下:7,11,10,
11,6,14,11,10,11,9.根据这组数据判断下列结论中错误的是
( )
B
A. 这组数据的众数是11 B. 这组数据的中位数是10
C. 这组数据的平均数是10 D. 这组数据的方差是4.6
6.(2023·珠海斗门区期末)为了解养殖鱼的生长情况,养鱼者从鱼塘中随机捕捞了20条鱼,称得它们的质量如下表:
质量/ 1.0 1.2 1.5 2
频数 4 5 8 3
(1)样本的中位数是 ____.
1.5
(2)如果鱼塘里有10 000条鱼,通过计算估计鱼塘共有多少千克的鱼.
解: ,
.
答:鱼塘大约共有14 000千克的鱼.
7.(2023·惠州惠城区期末)在“我的中国梦”演讲比赛中,有5名学生
参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自
己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩
的( )
A
A. 中位数 B. 众数 C. 平均数 D. 方差
8.(2023·惠州惠城区期末)惠城区横沥
镇的陈大叔承包了甲、乙两座小山,各栽
了100棵荔枝树,发现其成活率均为 ,
为了分析收成情况,他分别从两山上各随
(1)直接写出甲山的4棵荔枝树的产量的中位数.
解: .
机采摘了4棵树的荔枝,每棵的产量如折线统计图所示.
(2)分别计算甲、乙两座山的荔枝样本的平均数,并判断哪座山的样本的产量高.
[答案] (千克), (千克),
甲、乙两山的样本的产量一样多.
(3)用样本平均数估计甲、乙两座山的荔枝的产量总和.
[答案] 总产量为 (千克).
答:甲、乙两山荔枝的产量总和为7 760千克.
9.(2023·珠海香洲区期末)为普及“垃圾分类”知识,某校组织全校
学生参加了垃圾分类主题知识竞赛.为了解竞赛成绩,学校随机抽样调
查了七、八年级各10名学生的成绩 (单位:分),分数如下:
七年级10名学生竞赛成绩:92,83,99,89,99,86,100,81,92,
99;
八年级10名学生竞赛成绩中分布在 的成绩:93,94,95.
【整理数据】:
年级
七年级 2 2 4
八年级 1 2 3 4
【分析数据】:
年级 平均数 众数 中位数 方差
七年级 92 45.8
八年级 94 100 38.2
根据以上提供的信息,回答下列问题:
(1)填空: ___, ____, ____, _____.
2
99
92
94.5
(2)若该校七年级学生有300人,且全部参加竞赛,请估计七年级成绩高于90分的人数.
解: (人).
答:七年级成绩高于90分的人数大约为180人.
(3)请你根据以上信息,推断哪个年级的成绩更好,并说明理由(写出一条理由即可).
解:八年级成绩更好.理由:
从平均数看,八年级成绩的平均数大于七年级,所以八年级成绩更好.(答案不唯一)
