初中数学人教版七年级下册5.2.2 平行线的判定课件(20张PPT)
文档属性
| 名称 | 初中数学人教版七年级下册5.2.2 平行线的判定课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 752.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 10:39:52 | ||
图片预览




文档简介
(共20张PPT)
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?你能用定义和平行公理的推论解决吗?如果不能还有什么方法呢?
情境引入
A
B
P
你还记得如何用三角板和直尺画平行线吗?
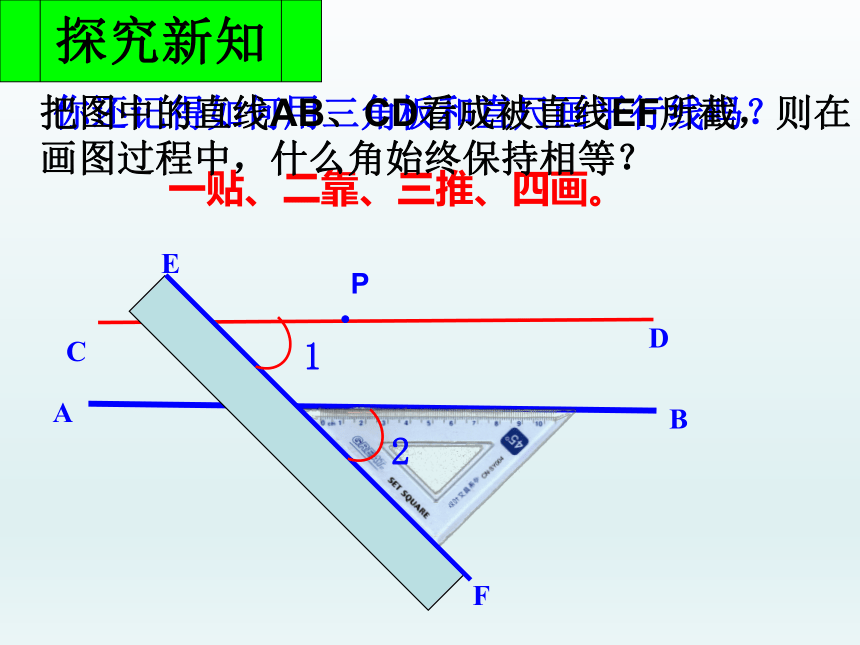
一贴、二靠、三推、四画。
C
D
1
2
探究新知
E
F
把图中的直线AB、CD看成被直线EF所截,则在
画图过程中,什么角始终保持相等?
把图中的直线AB、CD看成被直线EF所截,则在
画图过程中,什么角始终保持相等?
同位角
·
A
B
P
C
D
1
2
F
E
探究新知
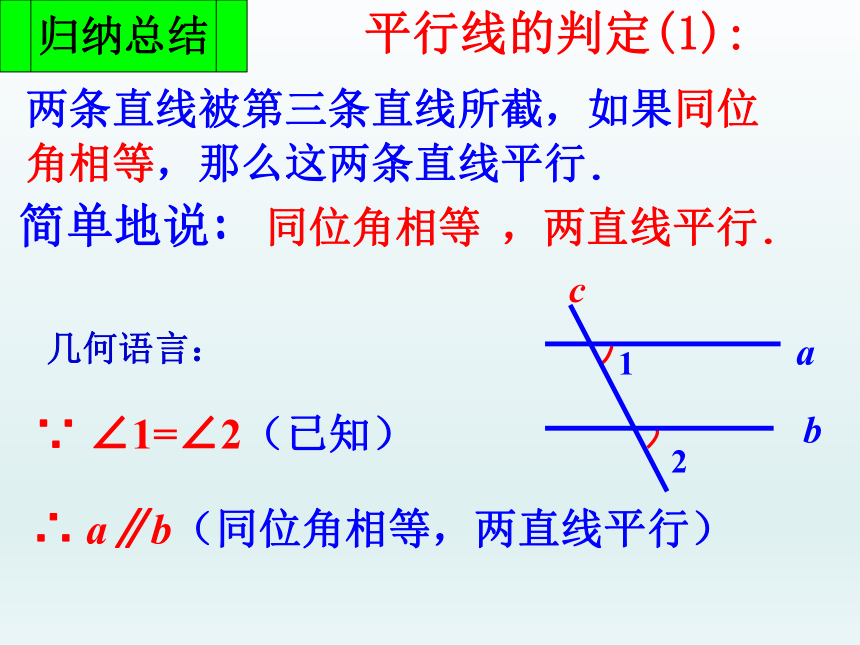
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
归纳总结
平行线的判定(1):
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
c
a
b
1
2
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
深入思考:
深入思考
继续探究
1
a
b
3
2
c
4
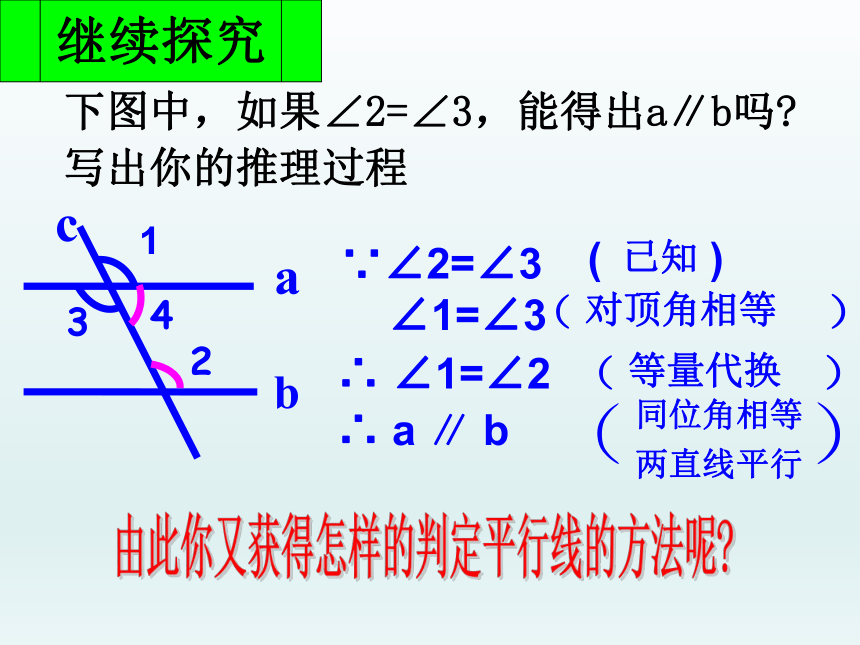
下图中,如果∠2=∠3,能得出a∥b吗
写出你的推理过程
∵∠2=∠3
∠1=∠3
∴ ∠1=∠2
∴ a ∥ b
( )
( )
对顶角相等
( )
等量代换
同位角相等
两直线平行
已知
( )
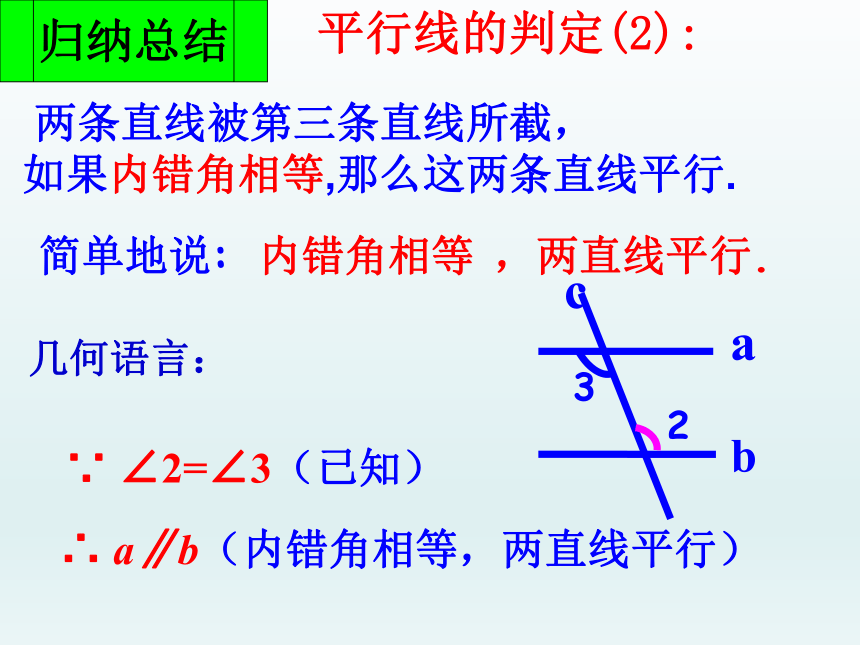
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.
简单地说: 内错角相等 ,两直线平行.
归纳总结
平行线的判定(2):
a
b
3
2
c
几何语言:
∵ ∠2=∠3(已知)
∴ a∥b(内错角相等,两直线平行)
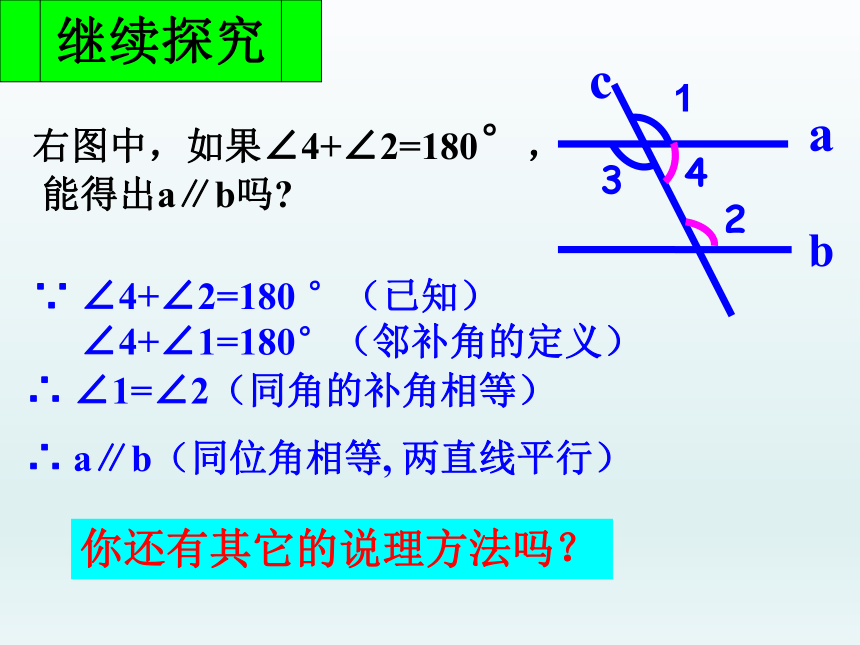
右图中,如果∠4+∠2=180°,
能得出a∥b吗
∵ ∠4+∠2=180 °(已知)
∠4+∠1=180°(邻补角的定义)
∴ ∠1=∠2(同角的补角相等)
∴ a∥b(同位角相等, 两直线平行)
你还有其它的说理方法吗?
继续探究
1
a
b
3
2
c
4
∴ ∠2=∠3(同角的补角相等)
∴ a∥b(内错角相等, 两直线平行)
下图中,如果∠4+∠2=180°,
能得出a∥b吗
探究新知
1
a
b
3
2
c
4
∵ ∠4+∠2=180 °(已知)
∠4+∠3=180°(邻补角的定义)
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.
简单地说:同旁内角互补,两直线平行.
平行线的判定(3):
归纳总结
a
b
c
1
2
几何语言:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
例. “在同一平面内,垂直于同一条直线的两条直线互相平行”吗?为什么?
解:平行.
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
理由如下:
a
b
c
1
2
>
>
范例点击
你还有其他方法吗?
(
3
4
(
1. 如图,若∠1=∠3,则 ∥ ;
若∠3=∠5,则 ∥ 。
牛刀小试
若∠4+∠5=180°,则_____∥_____,
其理由是 _________________;
若∠1=∠6,则_____∥_____,
其理由是 _________________ ;
AB
DE
BC
EF
BC
EF
同旁内角互补,两直线平行
AB
DE
内错角相等,两直线平行
从∠1=∠2,可以推出 ∥ ,
理由是 。
(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(2)从∠4=∠ ,可以推出AD∥BC,
理由是 。
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
3
内错角相等,两直线平行
2.如图
牛刀小试
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
解决问题
1
2
方案1:
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
解决问题
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案2:
解决问题
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案3:
解决问题
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
课堂小结
1. p14 练习 第1题
2. p15 1、 (1)
3. p17 第7题 (1)
作业布置
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?你能用定义和平行公理的推论解决吗?如果不能还有什么方法呢?
情境引入
A
B
P
你还记得如何用三角板和直尺画平行线吗?
一贴、二靠、三推、四画。
C
D
1
2
探究新知
E
F
把图中的直线AB、CD看成被直线EF所截,则在
画图过程中,什么角始终保持相等?
把图中的直线AB、CD看成被直线EF所截,则在
画图过程中,什么角始终保持相等?
同位角
·
A
B
P
C
D
1
2
F
E
探究新知
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
归纳总结
平行线的判定(1):
几何语言:
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
c
a
b
1
2
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
深入思考:
深入思考
继续探究
1
a
b
3
2
c
4
下图中,如果∠2=∠3,能得出a∥b吗
写出你的推理过程
∵∠2=∠3
∠1=∠3
∴ ∠1=∠2
∴ a ∥ b
( )
( )
对顶角相等
( )
等量代换
同位角相等
两直线平行
已知
( )
两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.
简单地说: 内错角相等 ,两直线平行.
归纳总结
平行线的判定(2):
a
b
3
2
c
几何语言:
∵ ∠2=∠3(已知)
∴ a∥b(内错角相等,两直线平行)
右图中,如果∠4+∠2=180°,
能得出a∥b吗
∵ ∠4+∠2=180 °(已知)
∠4+∠1=180°(邻补角的定义)
∴ ∠1=∠2(同角的补角相等)
∴ a∥b(同位角相等, 两直线平行)
你还有其它的说理方法吗?
继续探究
1
a
b
3
2
c
4
∴ ∠2=∠3(同角的补角相等)
∴ a∥b(内错角相等, 两直线平行)
下图中,如果∠4+∠2=180°,
能得出a∥b吗
探究新知
1
a
b
3
2
c
4
∵ ∠4+∠2=180 °(已知)
∠4+∠3=180°(邻补角的定义)
两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.
简单地说:同旁内角互补,两直线平行.
平行线的判定(3):
归纳总结
a
b
c
1
2
几何语言:
∵ ∠1+∠2=180°(已知)
∴ a∥b(同旁内角互补,两直线平行)
例. “在同一平面内,垂直于同一条直线的两条直线互相平行”吗?为什么?
解:平行.
∵b⊥a ,c ⊥a (已知)
∴b∥c
(同位角相等,两直线平行)
∴∠1= ∠2 = 90°
(垂直的定义)
理由如下:
a
b
c
1
2
>
>
范例点击
你还有其他方法吗?
(
3
4
(
1. 如图,若∠1=∠3,则 ∥ ;
若∠3=∠5,则 ∥ 。
牛刀小试
若∠4+∠5=180°,则_____∥_____,
其理由是 _________________;
若∠1=∠6,则_____∥_____,
其理由是 _________________ ;
AB
DE
BC
EF
BC
EF
同旁内角互补,两直线平行
AB
DE
内错角相等,两直线平行
从∠1=∠2,可以推出 ∥ ,
理由是 。
(3)从∠ABC +∠ =180,可以推出AB∥CD ,
理由是 。
(2)从∠4=∠ ,可以推出AD∥BC,
理由是 。
AB
内错角相等,两直线平行
CD
BCD
同旁内角互补,两直线平行
3
内错角相等,两直线平行
2.如图
牛刀小试
有一块木板,身边只有直尺和量角器,我们怎样才能知道它上下边缘是否平行?
解决问题
1
2
方案1:
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
解决问题
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案2:
解决问题
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
1
2
方案3:
解决问题
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
数量关系
位置关系
课堂小结
1. p14 练习 第1题
2. p15 1、 (1)
3. p17 第7题 (1)
作业布置
