华师大版八年级上册数学第13.5.3 角平分线的性质 教案
文档属性
| 名称 | 华师大版八年级上册数学第13.5.3 角平分线的性质 教案 | 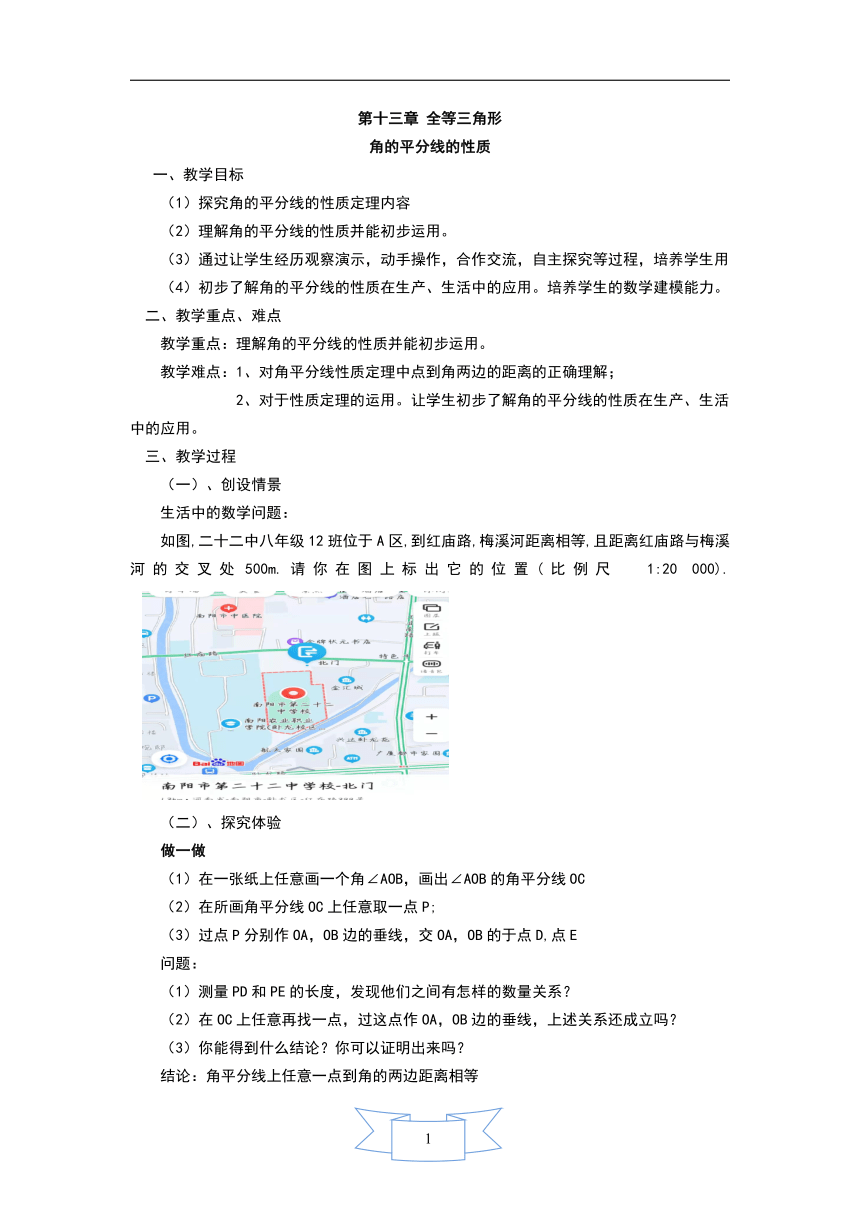 | |
| 格式 | doc | ||
| 文件大小 | 947.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 11:04:02 | ||
图片预览


文档简介
第十三章 全等三角形
角的平分线的性质
一、教学目标
(1)探究角的平分线的性质定理内容
(2)理解角的平分线的性质并能初步运用。
(3)通过让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用
(4)初步了解角的平分线的性质在生产、生活中的应用。培养学生的数学建模能力。
二、教学重点、难点
教学重点:理解角的平分线的性质并能初步运用。
教学难点:1、对角平分线性质定理中点到角两边的距离的正确理解;
2、对于性质定理的运用。让学生初步了解角的平分线的性质在生产、生活中的应用。
三、教学过程
(一)、创设情景
生活中的数学问题:
如图,二十二中八年级12班位于A区,到红庙路,梅溪河距离相等,且距离红庙路与梅溪河的交叉处500m.请你在图上标出它的位置(比例尺 1:20 000).
(二)、探究体验
做一做
在一张纸上任意画一个角∠AOB,画出∠AOB的角平分线OC
在所画角平分线OC上任意取一点P;
(3)过点P分别作OA,OB边的垂线,交OA,OB的于点D,点E
问题:
测量PD和PE的长度,发现他们之间有怎样的数量关系?
在OC上任意再找一点,过这点作OA,OB边的垂线,上述关系还成立吗?
你能得到什么结论?你可以证明出来吗?
结论:角平分线上任意一点到角的两边距离相等
(4)请学生自己写出已知求证验证结论的正确性。
利用三角形全等证明角平分线,进一步明确命题的题设与结论,熟悉几何证明过程。
利用多媒体直观优势,突破教学难点。
结合图形写出已知,求证,分析后写出证明过程。教师归纳,强调定理的条件和作用。
教师用文字语言叙述得到的结论。引导学生结合图形写出已知、求证,分析后写出证明过程,证明后,教师强调经过证明正确的命题可作为定理。同时强调文字命题的证明步骤。
(三)、巩固练习
判断正误,并说明理由:
(1)如图1,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF。
(2)如图2,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF。
(3)如图3,在∠AOB的平分线OC上任取一点P,若P到OA的距离为3cm,则P到OB的距离为3cm。
用多媒体展示判断题 ,学生独立思考完成,并请学生举手发表见解,教师予以肯定、鼓励。
让学生运用本节课所学的知识回答课前引例中的问题:
再次展示引例情景,用抢答的形式请同学们举手回答。
(四)、例题讲解
例 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F。求证:EB=FC。
变式:如图,在△ABC中,AB =AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足.
(1)求证 EB=FC.
(2)若∠A = 120°,判断△DEF的 形状并证明.
(3)连接AD,猜想AD与EF的关系,并证明
多媒体的运用,促进了课堂教学方法与模式的变革。
教师用多媒体展示问题,学生观察识图,独立思考,并且在小组内讨论交流,找出证明思路,再鼓励学生通过实物投影展示自己的证明过程,教师点评一题多变及一题多解。
通过学生观察识图、独立思考、小组讨论,培养学生合作交流的意识。
(五)、课堂小结
这节课你本节课学习了哪些知识?学会了什么方法?
定理 角平分线上的点到这个角的两边距离相等.
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
教师让学生畅谈本节课的收获与体会。学生归纳、梳理交流本节课所获得的知识技能与情感体验。
(六)、作业
1、必做题:课本第98页第1题
课本第99页第4题
2、选做题:课本第103复习题 第9题第12题
教师布置作业,学生独立完成。
板书设计:
13.5.3角平分线的性质
角平分线的性质定理: 例题 变式
角平分线上的点到角两边的距离相等.
几何语言描述:
OC平分∠AOB,P是OC上一点
且PD⊥OA于D, PE⊥OB于E.
∴ PD= PE.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:证明线段相等
A
O
B
P
E
F
图2
图3
A
O
B
P
E
A
O
B
P
E
F
图1
A
F
C
D
B
E
D
P
A
C
B
E
O
角的平分线的性质
一、教学目标
(1)探究角的平分线的性质定理内容
(2)理解角的平分线的性质并能初步运用。
(3)通过让学生经历观察演示,动手操作,合作交流,自主探究等过程,培养学生用
(4)初步了解角的平分线的性质在生产、生活中的应用。培养学生的数学建模能力。
二、教学重点、难点
教学重点:理解角的平分线的性质并能初步运用。
教学难点:1、对角平分线性质定理中点到角两边的距离的正确理解;
2、对于性质定理的运用。让学生初步了解角的平分线的性质在生产、生活中的应用。
三、教学过程
(一)、创设情景
生活中的数学问题:
如图,二十二中八年级12班位于A区,到红庙路,梅溪河距离相等,且距离红庙路与梅溪河的交叉处500m.请你在图上标出它的位置(比例尺 1:20 000).
(二)、探究体验
做一做
在一张纸上任意画一个角∠AOB,画出∠AOB的角平分线OC
在所画角平分线OC上任意取一点P;
(3)过点P分别作OA,OB边的垂线,交OA,OB的于点D,点E
问题:
测量PD和PE的长度,发现他们之间有怎样的数量关系?
在OC上任意再找一点,过这点作OA,OB边的垂线,上述关系还成立吗?
你能得到什么结论?你可以证明出来吗?
结论:角平分线上任意一点到角的两边距离相等
(4)请学生自己写出已知求证验证结论的正确性。
利用三角形全等证明角平分线,进一步明确命题的题设与结论,熟悉几何证明过程。
利用多媒体直观优势,突破教学难点。
结合图形写出已知,求证,分析后写出证明过程。教师归纳,强调定理的条件和作用。
教师用文字语言叙述得到的结论。引导学生结合图形写出已知、求证,分析后写出证明过程,证明后,教师强调经过证明正确的命题可作为定理。同时强调文字命题的证明步骤。
(三)、巩固练习
判断正误,并说明理由:
(1)如图1,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF。
(2)如图2,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF。
(3)如图3,在∠AOB的平分线OC上任取一点P,若P到OA的距离为3cm,则P到OB的距离为3cm。
用多媒体展示判断题 ,学生独立思考完成,并请学生举手发表见解,教师予以肯定、鼓励。
让学生运用本节课所学的知识回答课前引例中的问题:
再次展示引例情景,用抢答的形式请同学们举手回答。
(四)、例题讲解
例 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F。求证:EB=FC。
变式:如图,在△ABC中,AB =AC,D是BC边的中点,DE⊥AB,DF⊥AC,点E、F为垂足.
(1)求证 EB=FC.
(2)若∠A = 120°,判断△DEF的 形状并证明.
(3)连接AD,猜想AD与EF的关系,并证明
多媒体的运用,促进了课堂教学方法与模式的变革。
教师用多媒体展示问题,学生观察识图,独立思考,并且在小组内讨论交流,找出证明思路,再鼓励学生通过实物投影展示自己的证明过程,教师点评一题多变及一题多解。
通过学生观察识图、独立思考、小组讨论,培养学生合作交流的意识。
(五)、课堂小结
这节课你本节课学习了哪些知识?学会了什么方法?
定理 角平分线上的点到这个角的两边距离相等.
∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)
∴PD=PE(角平分线上的点到这个角的两边距离相等).
教师让学生畅谈本节课的收获与体会。学生归纳、梳理交流本节课所获得的知识技能与情感体验。
(六)、作业
1、必做题:课本第98页第1题
课本第99页第4题
2、选做题:课本第103复习题 第9题第12题
教师布置作业,学生独立完成。
板书设计:
13.5.3角平分线的性质
角平分线的性质定理: 例题 变式
角平分线上的点到角两边的距离相等.
几何语言描述:
OC平分∠AOB,P是OC上一点
且PD⊥OA于D, PE⊥OB于E.
∴ PD= PE.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:证明线段相等
A
O
B
P
E
F
图2
图3
A
O
B
P
E
A
O
B
P
E
F
图1
A
F
C
D
B
E
D
P
A
C
B
E
O
