27.3二次函数的实践与探索
图片预览



文档简介
课件24张PPT。
§27.3二次函数的实践与探索
待定系数法求二次函数关系式几种方法
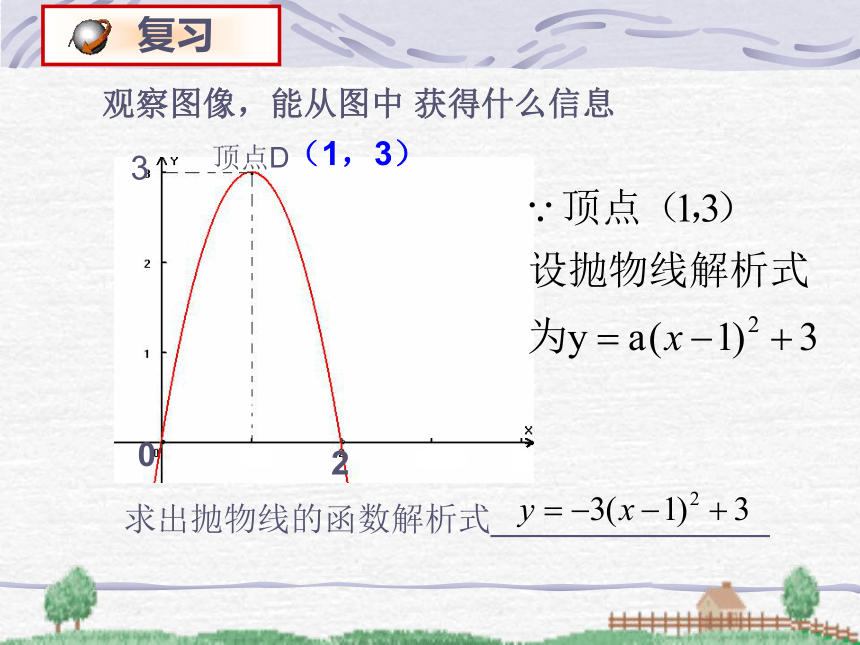
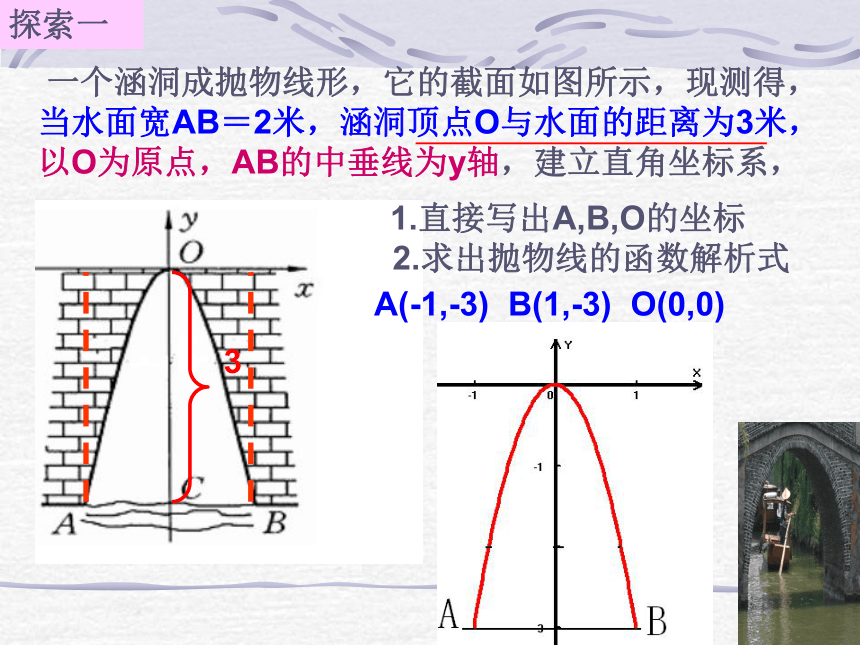
设一般式:设顶点式:观察图像,能从图中 获得什么信息230求出抛物线的函数解析式_______________ (1,3)顶点D一个涵洞成抛物线形, 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
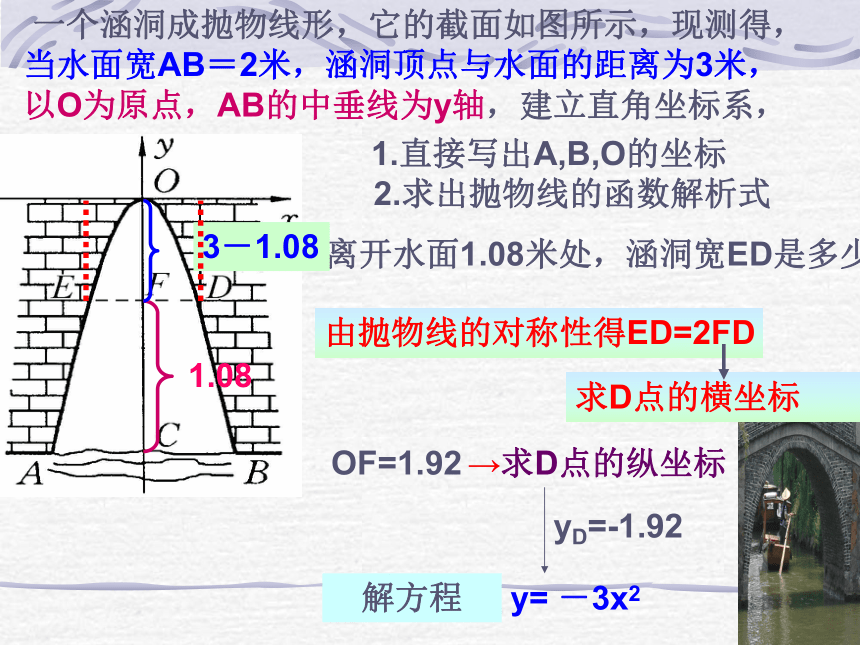
2.求出抛物线的函数解析式3A(-1,-3) B(1,-3) O(0,0)探索一 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3.离开水面1.08米处,涵洞宽ED是多少
1.083-1.08OF=1.92→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.92y= -3x2解方程小结找点坐标求解析式解决问题已知y求x,已知x求y点坐标一个涵洞成抛物线形,它的截面如图所示,现测得,
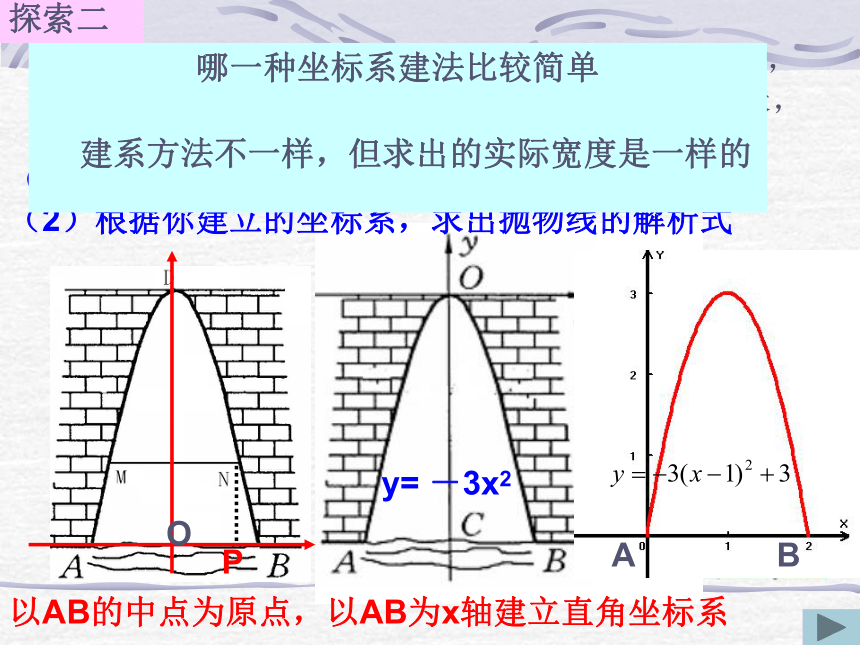
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
(2)根据你建立的坐标系,求出抛物线的解析式y= -3x2探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系O哪一种坐标系建法比较简单
建系方法不一样,但求出的实际宽度是一样的PAB图像可通过平移而得到(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FENNF→求N点的纵坐标oOF=0.8(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FE(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FEFNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高若箱子从涵洞正中通过,当通过的底为1.6时,能通过的最大高度为NF=1.08,小于正方体的高1.6,
所以不能通过
小结找点坐标求解析式解决问题已知y求x,已知x求y练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?
(货车视为长方体)8练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?
(货车视为长方体)8FN2当通过的底为2时,能通过的最大高度为NF,比较NF 与车的高CFCCF练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?8若要求车辆与隧道顶部的距离超过0.5米,能否通过(货车视为长方体)小结找点坐标求解析式解决问题已知y求x,已知x求y把实际问题转化为点坐标作业周末练习卷1.一个运动员推铅球,铅球在A点处出手,铅球的
飞行线路为抛物线铅球落地点为B,则这个运动员的成绩为__________米
2.
课后作业探索二O根据题目选择哪一种坐标系建法一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
(2)根据你建立的坐标系,求出抛物线的解析式探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系OP
§27.3二次函数的实践与探索
待定系数法求二次函数关系式几种方法
设一般式:设顶点式:观察图像,能从图中 获得什么信息230求出抛物线的函数解析式_______________ (1,3)顶点D一个涵洞成抛物线形, 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点O与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3A(-1,-3) B(1,-3) O(0,0)探索一 一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点与水面的距离为3米,
以O为原点,AB的中垂线为y轴,建立直角坐标系,1.直接写出A,B,O的坐标
2.求出抛物线的函数解析式3.离开水面1.08米处,涵洞宽ED是多少
1.083-1.08OF=1.92→求D点的纵坐标由抛物线的对称性得ED=2FD求D点的横坐标yD=-1.92y= -3x2解方程小结找点坐标求解析式解决问题已知y求x,已知x求y点坐标一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
(2)根据你建立的坐标系,求出抛物线的解析式y= -3x2探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系O哪一种坐标系建法比较简单
建系方法不一样,但求出的实际宽度是一样的PAB图像可通过平移而得到(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FENNF→求N点的纵坐标oOF=0.8(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FE(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FEFNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高(4)对称轴右侧0.8米的点F处,对应的涵洞壁离水面
的高是多少(NF=1.08)
(5)又一个边长为1.6米的正方体木箱,能否通过此
涵洞,说明理由(木箱底面与水面同一平面)FNc1.6当通过的底为1.6时,能通过的最大高度为NF,比较NF与正方体的高若箱子从涵洞正中通过,当通过的底为1.6时,能通过的最大高度为NF=1.08,小于正方体的高1.6,
所以不能通过
小结找点坐标求解析式解决问题已知y求x,已知x求y练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?
(货车视为长方体)8练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?
(货车视为长方体)8FN2当通过的底为2时,能通过的最大高度为NF,比较NF 与车的高CFCCF练习:
如图一个抛物线隧道,隧道离地面的最大高度为4米,
跨度为8米,隧道内设有双行道,在隧道正中间设
有隔离带(宽度不记),
一辆宽为2米,高为2.75米的货车能否通过隧道?8若要求车辆与隧道顶部的距离超过0.5米,能否通过(货车视为长方体)小结找点坐标求解析式解决问题已知y求x,已知x求y把实际问题转化为点坐标作业周末练习卷1.一个运动员推铅球,铅球在A点处出手,铅球的
飞行线路为抛物线铅球落地点为B,则这个运动员的成绩为__________米
2.
课后作业探索二O根据题目选择哪一种坐标系建法一个涵洞成抛物线形,它的截面如图所示,现测得,
当水面宽AB=2米,涵洞顶点D与水面的距离为3米,(1)建立适当的直角坐标系(几种建法)
(2)根据你建立的坐标系,求出抛物线的解析式探索二若水面上涨1米,则此时的水面宽MN为多少 以AB的中点为原点,以AB为x轴建立直角坐标系OP
