人教版三年级下册数学第八单元(数学广角——搭配《练习二十二》课件(27张PPT)
文档属性
| 名称 | 人教版三年级下册数学第八单元(数学广角——搭配《练习二十二》课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-27 19:37:40 | ||
图片预览





文档简介
(共27张PPT)
人教版三年级数学下册
第八单元 数学广角——搭配(二)
《练习二十二》
(课本第104页、105页)
课前律动操
学生操作
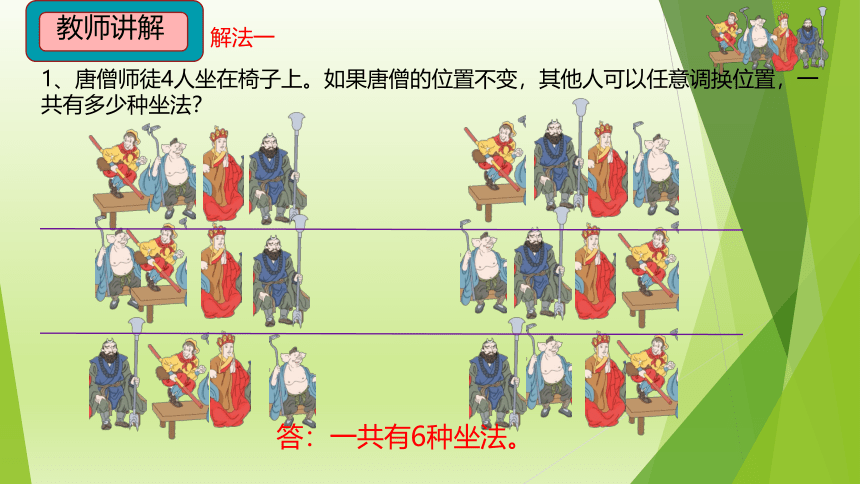
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法一
上面4个人物已经“打开授课克隆模式”。
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法一
教师讲解
答:一共有6种坐法。
学生操作
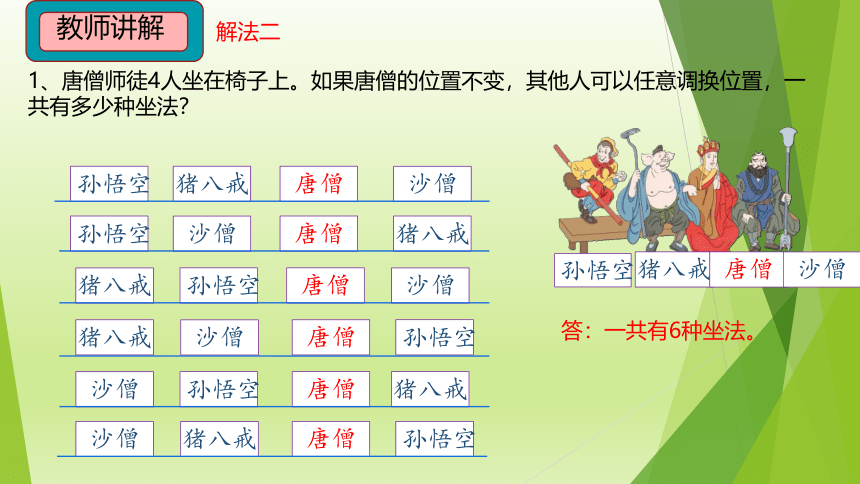
解法二
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
孙悟空
上面4个人物的名字卡片已经“打开授课克隆模式”。
猪八戒
唐僧
沙僧
答:一共有6种坐法。
教师讲解
孙悟空
猪八戒
唐僧
沙僧
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法二
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
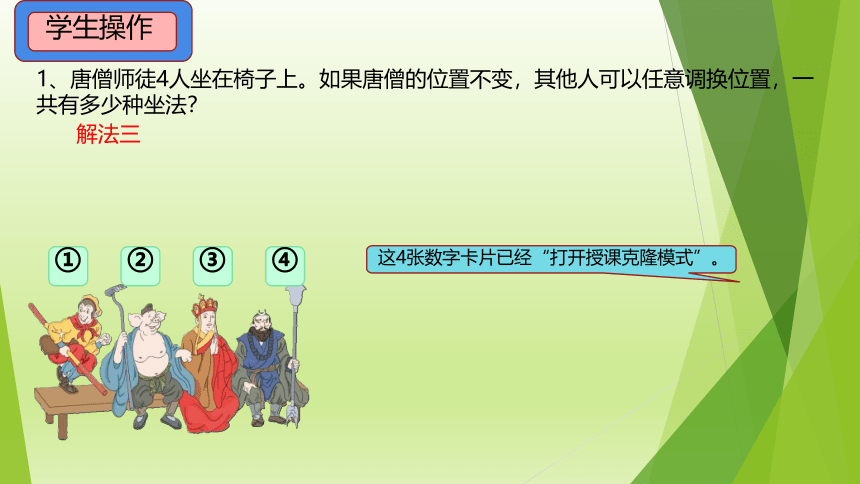
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
学生操作
①
②
④
③
这4张数字卡片已经“打开授课克隆模式”。
解法三
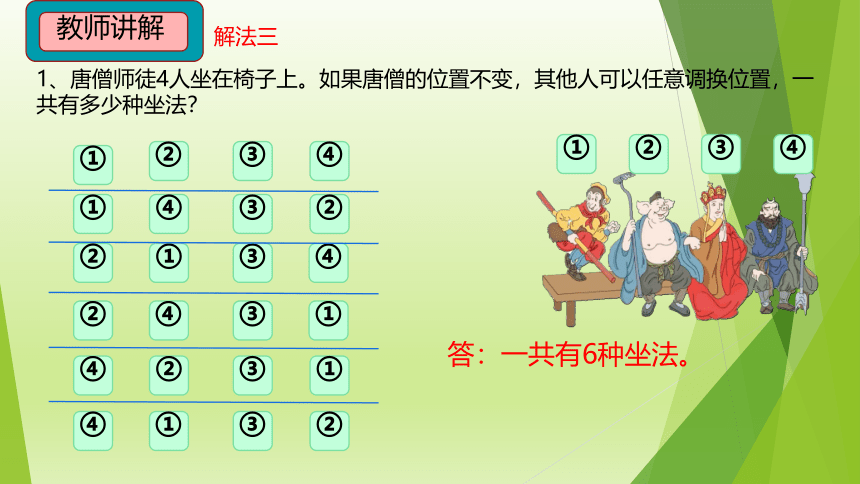
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
③
④
①
②
教师讲解
①
①
①
①
①
②
②
②
②
②
③
③
③
③
③
④
④
④
④
④
①
②
④
③
答:一共有6种坐法。
解法三
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
2
5
7
9
学生操作
这4张卡片已经打开授课克隆模式
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
答:能组成9个个位是单数的两位数。
2
5
7
9
固定个位法
教师讲解
2
2
2
5
5
5
5
7
7
7
7
7
9
9
9
9
9
5
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
答:能组成9个个位是单数的两位数。
2
5
7
9
固定十位法
教师讲解
2
2
2
5
5
5
5
7
7
7
7
7
9
9
9
9
9
5
右面4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A摆最左边有6种摆法。
B摆最左边有6种摆法。
D摆最左边有6种摆法。
答:一共有18摆法。
6╳3=18(种)
3.
A1
A2
B1
B2
B3
B4
A1
A2
B1
B2
B3
B4
一共要拍多少张照片?
答:一共要拍8张照片。
4.
A1
分别和别人合拍4次
A2
分别和别人合拍4次
4╳2=8(张)
右图中一共有多少个长方形?
由一个图形组成的长方形:
4个
答:右图中一共有9个长方形。
由两个图形组成的长方形:
4个
由四个图形组成的长方形:
1个
5.
从鸟岛到狮虎山,共有多少条路线?
答:从鸟岛到狮虎山,共有8条路线。
A1
A2
B1
B2
C1
C2
A1
→B1
→C1
A1
→B1
→C2
A1
→B2
→C1
A1
→B2
→C2
A2
→B1
→C1
A2
→B1
→C2
A2
→B2
→C1
A2
→B2
→C2
6.
甲、乙、丙、丁4人参加乒乓球小组赛,每2人比赛一场,一共要比赛多少场?
7.
甲
乙
丙
丁
答:一共要比赛6场。
(1)小明想从中任选2本,共有多少种选法?
答:共有6种选法。
8.
(2)小明想选《数学家的故事》和1本其他的书分别送给小红和小丽,共有多少种送法?
小红
小丽
A
B
C
D
AB
AC
AD
A
B
B
A
A
C
C
A
A
D
D
A
答:一共有6种送法。
8.
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
9.
5
学生操作
这5张数字卡片已经“打开授课克隆模式”。
0
7
6
.
(1)小于1而小数部分是三位的小数。
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
9.
5
学生操作
这5张数字卡片已经“打开授课克隆模式”。
0
7
6
.
(2)大于7而小数部分是三位的小数。
(1)小于1而小数部分是三位的小数。
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(2)大于7而小数部分是三位的小数。
0.567
0.576
0.657
0.675
0.756
0.765
7.056
7.065
7.506
7.560
7.605
7.650
9.
教师讲解
从100到300的数中,有多少个十位和个位相同的数?
十
个
百
1
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
十
个
百
2
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
十
个
百
3
0 0
10+10+1=21(个)
答:共有21个十位和个位相同的数。
10.
本节课结束了,你有什么收获?
接下来是玩游戏时间!
人教版三年级数学下册
第八单元 数学广角——搭配(二)
《练习二十二》
(课本第104页、105页)
课前律动操
学生操作
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法一
上面4个人物已经“打开授课克隆模式”。
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法一
教师讲解
答:一共有6种坐法。
学生操作
解法二
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
孙悟空
上面4个人物的名字卡片已经“打开授课克隆模式”。
猪八戒
唐僧
沙僧
答:一共有6种坐法。
教师讲解
孙悟空
猪八戒
唐僧
沙僧
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
解法二
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
孙悟空
猪八戒
唐僧
沙僧
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
学生操作
①
②
④
③
这4张数字卡片已经“打开授课克隆模式”。
解法三
1、唐僧师徒4人坐在椅子上。如果唐僧的位置不变,其他人可以任意调换位置,一 共有多少种坐法?
③
④
①
②
教师讲解
①
①
①
①
①
②
②
②
②
②
③
③
③
③
③
④
④
④
④
④
①
②
④
③
答:一共有6种坐法。
解法三
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
2
5
7
9
学生操作
这4张卡片已经打开授课克隆模式
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
答:能组成9个个位是单数的两位数。
2
5
7
9
固定个位法
教师讲解
2
2
2
5
5
5
5
7
7
7
7
7
9
9
9
9
9
5
用2、5、7、9能组成没有重复数字的两位数,能组成多少个个位是单数的两位数?
2.
答:能组成9个个位是单数的两位数。
2
5
7
9
固定十位法
教师讲解
2
2
2
5
5
5
5
7
7
7
7
7
9
9
9
9
9
5
右面4个分类垃圾桶摆成一排,其中“其它垃圾”桶不能摆在最左边,这样的摆法一共有多少种?
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A摆最左边有6种摆法。
B摆最左边有6种摆法。
D摆最左边有6种摆法。
答:一共有18摆法。
6╳3=18(种)
3.
A1
A2
B1
B2
B3
B4
A1
A2
B1
B2
B3
B4
一共要拍多少张照片?
答:一共要拍8张照片。
4.
A1
分别和别人合拍4次
A2
分别和别人合拍4次
4╳2=8(张)
右图中一共有多少个长方形?
由一个图形组成的长方形:
4个
答:右图中一共有9个长方形。
由两个图形组成的长方形:
4个
由四个图形组成的长方形:
1个
5.
从鸟岛到狮虎山,共有多少条路线?
答:从鸟岛到狮虎山,共有8条路线。
A1
A2
B1
B2
C1
C2
A1
→B1
→C1
A1
→B1
→C2
A1
→B2
→C1
A1
→B2
→C2
A2
→B1
→C1
A2
→B1
→C2
A2
→B2
→C1
A2
→B2
→C2
6.
甲、乙、丙、丁4人参加乒乓球小组赛,每2人比赛一场,一共要比赛多少场?
7.
甲
乙
丙
丁
答:一共要比赛6场。
(1)小明想从中任选2本,共有多少种选法?
答:共有6种选法。
8.
(2)小明想选《数学家的故事》和1本其他的书分别送给小红和小丽,共有多少种送法?
小红
小丽
A
B
C
D
AB
AC
AD
A
B
B
A
A
C
C
A
A
D
D
A
答:一共有6种送法。
8.
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
9.
5
学生操作
这5张数字卡片已经“打开授课克隆模式”。
0
7
6
.
(1)小于1而小数部分是三位的小数。
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
9.
5
学生操作
这5张数字卡片已经“打开授课克隆模式”。
0
7
6
.
(2)大于7而小数部分是三位的小数。
(1)小于1而小数部分是三位的小数。
按下面的要求,用5、0、7和6这几个数字写出没有重复数字的小数。
(2)大于7而小数部分是三位的小数。
0.567
0.576
0.657
0.675
0.756
0.765
7.056
7.065
7.506
7.560
7.605
7.650
9.
教师讲解
从100到300的数中,有多少个十位和个位相同的数?
十
个
百
1
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
十
个
百
2
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
十
个
百
3
0 0
10+10+1=21(个)
答:共有21个十位和个位相同的数。
10.
本节课结束了,你有什么收获?
接下来是玩游戏时间!
