沪教版六年级数学下册 8.4长方体中棱与平面位置关系的认识 试题(含解析)
文档属性
| 名称 | 沪教版六年级数学下册 8.4长方体中棱与平面位置关系的认识 试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 225.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览

文档简介
8.4长方体中棱与平面位置关系的认识
一、单选题
1.下列说法中,错误的是( )
A.旗杆垂直于地面 B.墙面一般垂直于地面
C.东方明珠电视塔垂直于地面 D.树木一定垂直于地面
2.在长方体中,与一个面垂直的棱有( )
A.2条 B.3条 C.4条 D.6条
3.长方体中,与一条棱异面的棱有( )
A.2条 B.3条 C.4条 D.6条
4.下面不能用来检验直线与平面垂直的工具是( )
A.长方形纸片 B.合页型折纸 C.铅垂线 D.三角尺
5.下列关于长方体的说法中正确的是( )
A.最少有4条棱相等 B.最多有8条棱相等
C.最多有2个面相等 D.最多有5个面相等
6.如图所示几何体的主视图为( )
A. B. C. D.
二、填空题
7.如图所示:
(1)与线段垂直的面有____________________________.
(2)与面垂直的线段有____________________________.
(3)与线段平行的线段有____________________________.
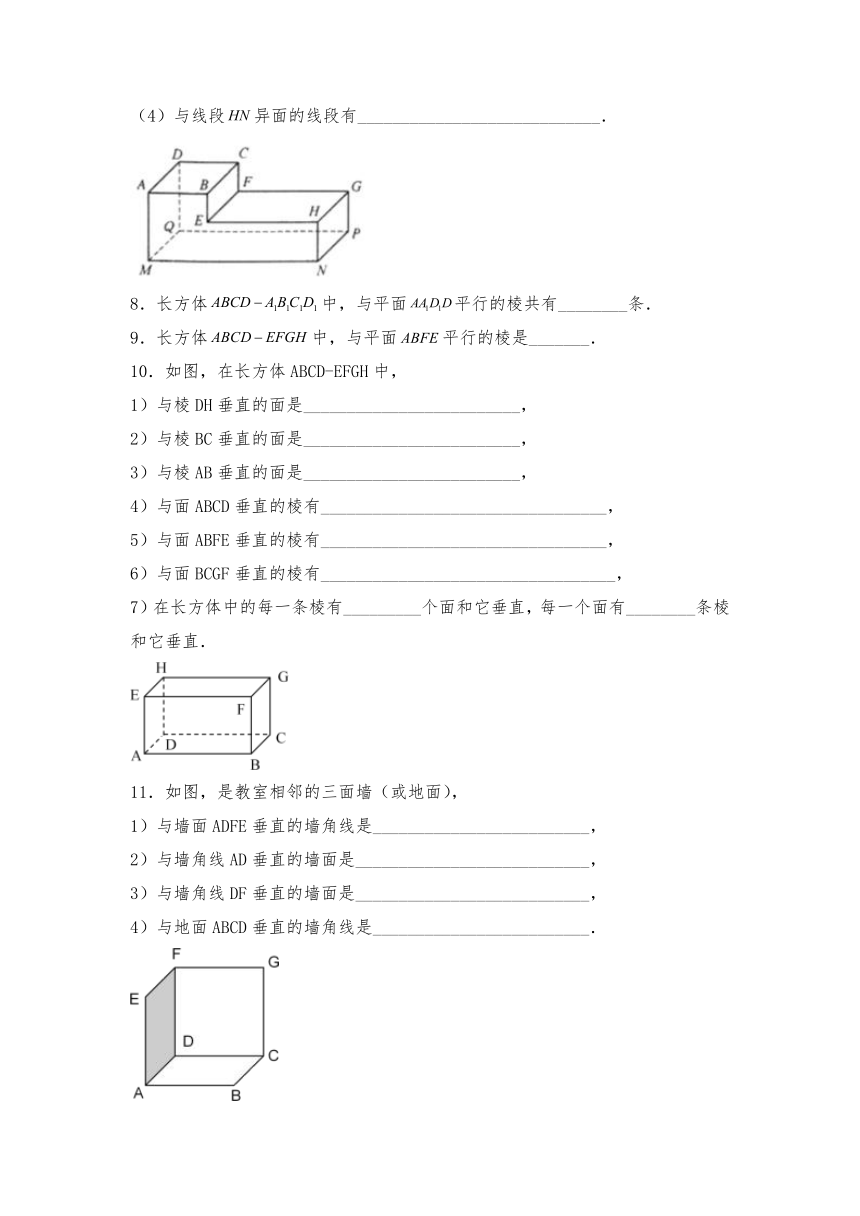
(4)与线段异面的线段有____________________________.
8.长方体中,与平面平行的棱共有________条.
9.长方体中,与平面平行的棱是_______.
10.如图,在长方体ABCD-EFGH中,
1)与棱DH垂直的面是_________________________,
2)与棱BC垂直的面是_________________________,
3)与棱AB垂直的面是_________________________,
4)与面ABCD垂直的棱有_________________________________,
5)与面ABFE垂直的棱有_________________________________,
6)与面BCGF垂直的棱有__________________________________,
7)在长方体中的每一条棱有_________个面和它垂直,每一个面有________条棱和它垂直.
11.如图,是教室相邻的三面墙(或地面),
1)与墙面ADFE垂直的墙角线是_________________________,
2)与墙角线AD垂直的墙面是___________________________,
3)与墙角线DF垂直的墙面是___________________________,
4)与地面ABCD垂直的墙角线是_________________________.
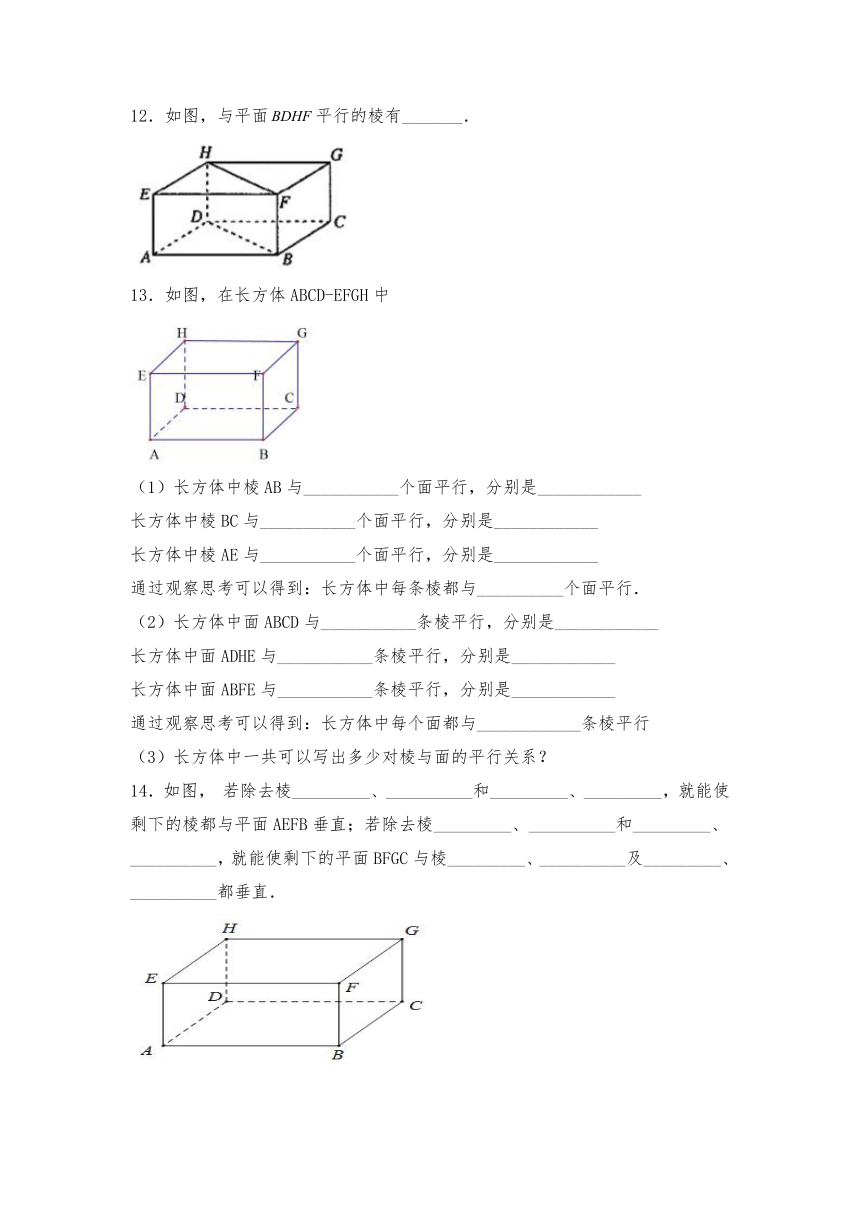
12.如图,与平面平行的棱有_______.
13.如图,在长方体ABCD-EFGH中
(1)长方体中棱AB与___________个面平行,分别是____________
长方体中棱BC与___________个面平行,分别是____________
长方体中棱AE与___________个面平行,分别是____________
通过观察思考可以得到:长方体中每条棱都与__________个面平行.
(2)长方体中面ABCD与___________条棱平行,分别是____________
长方体中面ADHE与___________条棱平行,分别是____________
长方体中面ABFE与___________条棱平行,分别是____________
通过观察思考可以得到:长方体中每个面都与____________条棱平行
(3)长方体中一共可以写出多少对棱与面的平行关系?
14.如图, 若除去棱_________、__________和_________、_________,就能使剩下的棱都与平面AEFB垂直;若除去棱_________、__________和_________、__________,就能使剩下的平面BFGC与棱_________、__________及_________、__________都垂直.
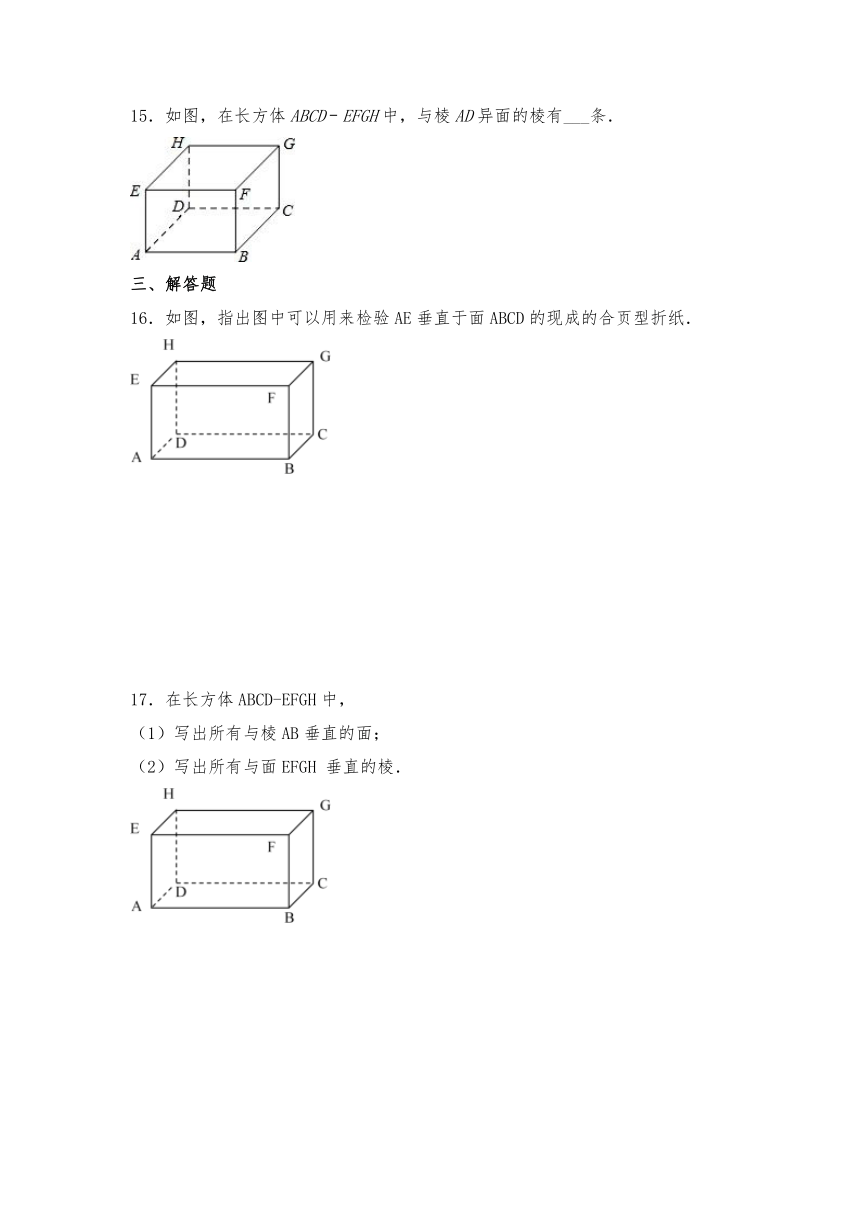
15.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有___条.
三、解答题
16.如图,指出图中可以用来检验AE垂直于面ABCD的现成的合页型折纸.
17.在长方体ABCD-EFGH中,
(1)写出所有与棱AB垂直的面;
(2)写出所有与面EFGH 垂直的棱.
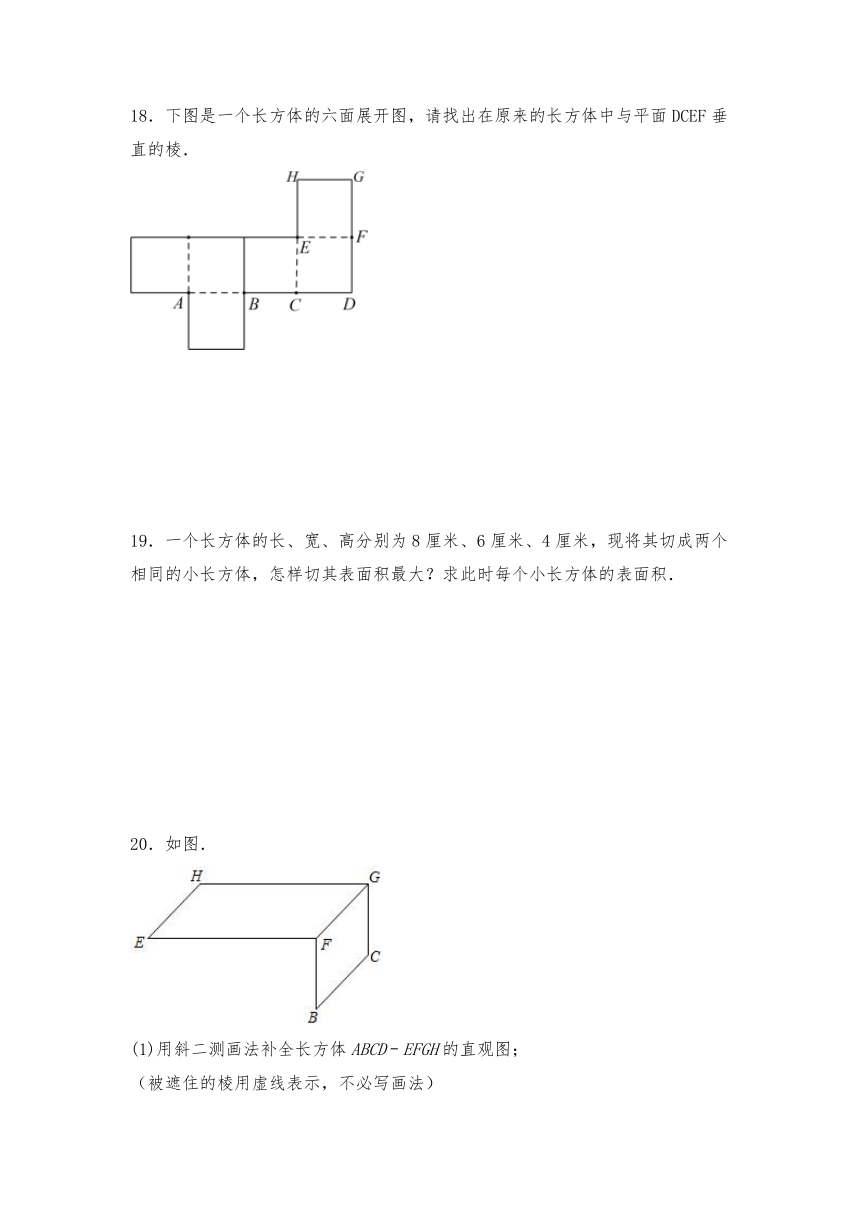
18.下图是一个长方体的六面展开图,请找出在原来的长方体中与平面DCEF垂直的棱.
19.一个长方体的长、宽、高分别为8厘米、6厘米、4厘米,现将其切成两个相同的小长方体,怎样切其表面积最大?求此时每个小长方体的表面积.
20.如图.
(1)用斜二测画法补全长方体ABCD﹣EFGH的直观图;
(被遮住的棱用虚线表示,不必写画法)
(2)长方体中与棱FG平行的平面有 ;
(3)联结HF、DB,与平面HFBD垂直的面有 .
答案
一、单选题
1.D
【思路指引】
根据实际情况逐一分析即可.
【详解详析】
解:A. 旗杆一般垂直于地面,故正确;
B. 墙面一般垂直于地面,故正确;
C. 东方明珠电视塔垂直于地面,故正确;
D.在山坡上的树木不一定垂直于地面,大多数是垂直于水平面的,故错误.
故选D.
2.C
【思路指引】
根据长方体中棱和面的位置关系进行选择.
【详解详析】
长方体中与一个面垂直的棱有4条.
故选:C.
3.C
【思路指引】
由题意根据长方体中棱与平面位置关系可知与一条棱异面的平面上所有棱长都异面,以此进行分析即可得出答案.
【详解详析】
解:因为与一条棱异面的平面上有4条棱长,
所以长方体中,与一条棱异面的棱有4条.
故选:C.
4.A
【思路指引】
根据长方体中棱与面的位置关系,逐项分析判定可知.
【详解详析】
解:铅垂线,三角尺,合页型折纸可以用来检验直线与平面是否垂直,
而长方形纸片只能判断两条直线互相垂直,不能判断直线与平面是否垂直,
故选:A.
5.A
【思路指引】
根据长方体的特征:相对的面面积相等,所以长方体中至少有2个面的面积相等,如果长方体有2个面是正方形,最多有4个面的面积相等;长方体的长、宽、高如果有两个相等,这时最多有8条棱的长度相等,据此解答即可.
【详解详析】
解:长方体有6个面,8个顶点,12条棱.长方体每个面都是长方形,特殊情况有两个面是正方形,长方体的12条棱中至少有4条棱相等,最多有8条棱的长度相等,最多有4个面相等,
故选:A.
6.D
【思路指引】
根据从正面看得到的图形为主视图,即可求解;
【详解详析】
从正面看:
故选:D.
二、填空题
7.(1)面、面、面;(2)、、、、、;(3)、、、、;(4)、、、、、、.
【思路指引】
(1)根据题意及图形可直接得出答案;
(2)根据长方体中棱与面的位置关系可直接解答;
(3)根据长方体中的棱与棱的位置关系可直接作答;
(4)根据长方体中棱与棱的位置关系可直接作答.
【详解详析】
如图所示:
(1)与线段垂直的面有:面、面、面;
(2)与面垂直的线段有:、、、、、;
(3)与线段平行的线段有:、、、、;
(4)与线段异面的线段有:、、、、、、.
故答案为(1)面、面、面;(2)、、、、、;(3)、、、、;(4)、、、、、、.
8.4
【思路指引】
根据题意,画出图形,即可得出结论.
【详解详析】
解:如图所示,与平面平行的棱有BC、,共有4条
故答案为:4.
9.棱、、、
【思路指引】
由题意直接根据长方体的结构特征,结合平行线的定义进行分析作答.
【详解详析】
解:如图:
可得长方体中,与平面平行的棱是棱、、、.
故答案为:棱、、、.
10. 面ABCD、面EFGH 面ABFE、面DCGH 面ADHE、面BCGF 棱AE、棱BF、棱CG、棱DH 棱AD、棱BC、棱FG、棱EH 棱AB、棱CD、棱HG、棱EF 两 四
【思路指引】
根据棱和平面垂直的检验方法,可以采用“铅锤法”、“三角尺法”或者“合页型折纸法”进行,检验长方体中棱和面的垂直关系,由此得到对应的面或者棱,并表示出来.
【详解详析】
利用“铅锤法”、“三角尺法”或者“合页型折纸法”可得知与棱DH垂直的面是面ABCD、面EFGH;与棱BC垂直的面是面ABFE、面DCGH;与棱AB垂直的面是面ADHE、面BCGF;与面ABCD垂直的棱有棱AE、棱BF、棱CG、棱DH;与面ABFE垂直的棱有棱AD、棱BC、棱FG、棱EH;与面BCGF垂直的棱有棱AB、棱CD、棱HG、棱EF;在长方体中的每一条棱有两个面和它垂直,每一个面有四条棱和它垂直.
故答案为:(1)面ABCD、面EFGH.
(2)面ABFE、面DCGH.
(3)面ADHE、面BCGF.
(4)棱AE、棱BF、棱CG、棱DH.
(5)棱AD、棱BC、棱FG、棱EH.
(6)棱AB、棱CD、棱HG、棱EF.
(7)两 四.
11. 棱CD 面DCGF 面ABCD 棱DF
【思路指引】
根据题意,利用长方体中棱与平面的位置关系来判断题目中棱与面的垂直关系.
【详解详析】
(1)与墙面ADFE垂直的墙角线是棱CD;
(2)与墙角线AD垂直的墙面是面DCGF;
(3)与墙角线DF垂直的墙面是面ABCD;
(4)与地面ABCD垂直的墙角线是棱DF.
故答案是:棱CD;面DCGF;面ABCD;棱DF.
12.棱、
【思路指引】
直接根据长方体中棱与平面的位置关系进行解答即可.
【详解详析】
如图所示:与平面平行的棱有棱、,
故答案为棱、.
13.(1)两,面EFGH、面CDHG;两,面ADHE、面EFGH;两,面BCGF、面CDHG;两;(2)四,棱EF、棱FG、棱GH、棱HE;四,棱BC、棱CG、棱GF、棱FB;四,棱CD、棱DH、棱HG、棱GC;四,(3)12对
【思路指引】
根据长方体棱与面之间的关系解答即可.
【详解详析】
(1)长方体中棱AB与两个面平行,分别是:面EFGH、面CDHG;
长方体中棱BC与两个面平行,分别是:面ADHE、面EFGH;
长方体中棱AE与两个面平行,分别是:面BCGF、面CDHG;
通过观察思考可以得到:长方体中每条棱都与两个面平行.
故答案为:两,面EFGH、面CDHG;两,面ADHE、面EFGH;两,面BCGF、面CDHG;两;
(2)长方体中面ABCD与四条棱平行,分别是:棱EF、棱FG、棱GH、棱HE;
长方体中面ADHE与四条棱平行,分别是:棱BC、棱CG、棱GF、棱FB;
长方体中面ABFE与四条棱平行,分别是:棱CD、棱DH、棱HG、棱GC;
通过观察思考可以得到:长方体中每个面都与四条棱平行;
故答案为:四,棱EF、棱FG、棱GH、棱HE;四,棱BC、棱CG、棱GF、棱FB;四,棱CD、棱DH、棱HG、棱GC;四;
(3)长方体中一共可以写出12对棱与面的平行关系.
如:棱AB与面EFGH;棱BC与面ADHE;棱CD与面ABFE;棱AD与面BCGF;棱EF与面ABCD;棱FG与面ADHE;棱GH与面ABCD;棱EH与面BCGF;棱AE与面BCGF;棱BF与面DCGH;棱CG与面ADHE;棱DH与面ABFE.
14.棱CD,棱DH,棱GH,棱CG,棱AD,棱DH,棱HE,棱EA,棱EF,棱AB,棱DC,棱HG
【思路指引】
根据长方体的特征,观察可得出结果.
【详解详析】
根据长方体的特征,与平面AEFB垂直的棱有棱棱CD,棱DH,棱GH,棱CG,
因此,若去掉长方体中的棱棱AD,棱DH,棱HE,棱EA,
则剩下的棱棱EF,棱AB,棱DC,棱HG都能与平面BFGC垂直,
故答案为:棱CD,棱DH,棱GH,棱CG,棱AD,棱DH,棱HE,棱EA,棱EF,棱AB,棱DC,棱HG.
15.4
【思路指引】
异面指不在同一个平面内,AD可看作在下面和左面两个平面内,只要不在下面和左面内的棱即可.
【详解详析】
解:棱AD异面的棱:BF、CG、EF、HG,
故答案为:4.
三、解答题
16.
解:如果把面ADHE和面ABFE组成的图形看作直立于面ABCD上的合页型折纸,那么可以说明棱AE⊥平面 ABCD.
∴图中可以用来检验AE垂直于面ABCD的现成的合页型折纸是面ADHE和面ABFE.
17.
(1)与棱AB垂直的面有两个:面CBGF、面ADHE;
(2)与面EFGH 垂直的棱有棱AE、棱BF、棱CG、棱DH.
18.
解:根据题意,
与平面DCEF垂直的棱有:棱FG、棱EH、棱CB、棱AD.共4条.
19.
解:把一个长方体切成两个长方体,只切一次,增加两个横截面,
所以只要增加的两个横截面的面积最大,则切成的表面积就最大,
所以应该按照高来切,平分成两个小长方体,切的横截面即为长×宽,
此时每一个小长方体的表面积为:2×(8×6)+2×(8×2)+2×(6×2)=96+32+24=152平面厘米,
故答案为:按照高来切,平分成两个小长方体;每个小长方体表面积为152平方厘米.
20.
(1)
如图,长方体ABCD﹣EFGH即为所求.
(2)
与棱FG平行的平面有平面ADHE,平面ABCD.
故答案为:平面ADHE,平面ABCD.
(3)
与平面HFBD垂直的平面有平面ABCD,平面EFGH.
故答案为:平面ABCD,平面EFGH.
一、单选题
1.下列说法中,错误的是( )
A.旗杆垂直于地面 B.墙面一般垂直于地面
C.东方明珠电视塔垂直于地面 D.树木一定垂直于地面
2.在长方体中,与一个面垂直的棱有( )
A.2条 B.3条 C.4条 D.6条
3.长方体中,与一条棱异面的棱有( )
A.2条 B.3条 C.4条 D.6条
4.下面不能用来检验直线与平面垂直的工具是( )
A.长方形纸片 B.合页型折纸 C.铅垂线 D.三角尺
5.下列关于长方体的说法中正确的是( )
A.最少有4条棱相等 B.最多有8条棱相等
C.最多有2个面相等 D.最多有5个面相等
6.如图所示几何体的主视图为( )
A. B. C. D.
二、填空题
7.如图所示:
(1)与线段垂直的面有____________________________.
(2)与面垂直的线段有____________________________.
(3)与线段平行的线段有____________________________.
(4)与线段异面的线段有____________________________.
8.长方体中,与平面平行的棱共有________条.
9.长方体中,与平面平行的棱是_______.
10.如图,在长方体ABCD-EFGH中,
1)与棱DH垂直的面是_________________________,
2)与棱BC垂直的面是_________________________,
3)与棱AB垂直的面是_________________________,
4)与面ABCD垂直的棱有_________________________________,
5)与面ABFE垂直的棱有_________________________________,
6)与面BCGF垂直的棱有__________________________________,
7)在长方体中的每一条棱有_________个面和它垂直,每一个面有________条棱和它垂直.
11.如图,是教室相邻的三面墙(或地面),
1)与墙面ADFE垂直的墙角线是_________________________,
2)与墙角线AD垂直的墙面是___________________________,
3)与墙角线DF垂直的墙面是___________________________,
4)与地面ABCD垂直的墙角线是_________________________.
12.如图,与平面平行的棱有_______.
13.如图,在长方体ABCD-EFGH中
(1)长方体中棱AB与___________个面平行,分别是____________
长方体中棱BC与___________个面平行,分别是____________
长方体中棱AE与___________个面平行,分别是____________
通过观察思考可以得到:长方体中每条棱都与__________个面平行.
(2)长方体中面ABCD与___________条棱平行,分别是____________
长方体中面ADHE与___________条棱平行,分别是____________
长方体中面ABFE与___________条棱平行,分别是____________
通过观察思考可以得到:长方体中每个面都与____________条棱平行
(3)长方体中一共可以写出多少对棱与面的平行关系?
14.如图, 若除去棱_________、__________和_________、_________,就能使剩下的棱都与平面AEFB垂直;若除去棱_________、__________和_________、__________,就能使剩下的平面BFGC与棱_________、__________及_________、__________都垂直.
15.如图,在长方体ABCD﹣EFGH中,与棱AD异面的棱有___条.
三、解答题
16.如图,指出图中可以用来检验AE垂直于面ABCD的现成的合页型折纸.
17.在长方体ABCD-EFGH中,
(1)写出所有与棱AB垂直的面;
(2)写出所有与面EFGH 垂直的棱.
18.下图是一个长方体的六面展开图,请找出在原来的长方体中与平面DCEF垂直的棱.
19.一个长方体的长、宽、高分别为8厘米、6厘米、4厘米,现将其切成两个相同的小长方体,怎样切其表面积最大?求此时每个小长方体的表面积.
20.如图.
(1)用斜二测画法补全长方体ABCD﹣EFGH的直观图;
(被遮住的棱用虚线表示,不必写画法)
(2)长方体中与棱FG平行的平面有 ;
(3)联结HF、DB,与平面HFBD垂直的面有 .
答案
一、单选题
1.D
【思路指引】
根据实际情况逐一分析即可.
【详解详析】
解:A. 旗杆一般垂直于地面,故正确;
B. 墙面一般垂直于地面,故正确;
C. 东方明珠电视塔垂直于地面,故正确;
D.在山坡上的树木不一定垂直于地面,大多数是垂直于水平面的,故错误.
故选D.
2.C
【思路指引】
根据长方体中棱和面的位置关系进行选择.
【详解详析】
长方体中与一个面垂直的棱有4条.
故选:C.
3.C
【思路指引】
由题意根据长方体中棱与平面位置关系可知与一条棱异面的平面上所有棱长都异面,以此进行分析即可得出答案.
【详解详析】
解:因为与一条棱异面的平面上有4条棱长,
所以长方体中,与一条棱异面的棱有4条.
故选:C.
4.A
【思路指引】
根据长方体中棱与面的位置关系,逐项分析判定可知.
【详解详析】
解:铅垂线,三角尺,合页型折纸可以用来检验直线与平面是否垂直,
而长方形纸片只能判断两条直线互相垂直,不能判断直线与平面是否垂直,
故选:A.
5.A
【思路指引】
根据长方体的特征:相对的面面积相等,所以长方体中至少有2个面的面积相等,如果长方体有2个面是正方形,最多有4个面的面积相等;长方体的长、宽、高如果有两个相等,这时最多有8条棱的长度相等,据此解答即可.
【详解详析】
解:长方体有6个面,8个顶点,12条棱.长方体每个面都是长方形,特殊情况有两个面是正方形,长方体的12条棱中至少有4条棱相等,最多有8条棱的长度相等,最多有4个面相等,
故选:A.
6.D
【思路指引】
根据从正面看得到的图形为主视图,即可求解;
【详解详析】
从正面看:
故选:D.
二、填空题
7.(1)面、面、面;(2)、、、、、;(3)、、、、;(4)、、、、、、.
【思路指引】
(1)根据题意及图形可直接得出答案;
(2)根据长方体中棱与面的位置关系可直接解答;
(3)根据长方体中的棱与棱的位置关系可直接作答;
(4)根据长方体中棱与棱的位置关系可直接作答.
【详解详析】
如图所示:
(1)与线段垂直的面有:面、面、面;
(2)与面垂直的线段有:、、、、、;
(3)与线段平行的线段有:、、、、;
(4)与线段异面的线段有:、、、、、、.
故答案为(1)面、面、面;(2)、、、、、;(3)、、、、;(4)、、、、、、.
8.4
【思路指引】
根据题意,画出图形,即可得出结论.
【详解详析】
解:如图所示,与平面平行的棱有BC、,共有4条
故答案为:4.
9.棱、、、
【思路指引】
由题意直接根据长方体的结构特征,结合平行线的定义进行分析作答.
【详解详析】
解:如图:
可得长方体中,与平面平行的棱是棱、、、.
故答案为:棱、、、.
10. 面ABCD、面EFGH 面ABFE、面DCGH 面ADHE、面BCGF 棱AE、棱BF、棱CG、棱DH 棱AD、棱BC、棱FG、棱EH 棱AB、棱CD、棱HG、棱EF 两 四
【思路指引】
根据棱和平面垂直的检验方法,可以采用“铅锤法”、“三角尺法”或者“合页型折纸法”进行,检验长方体中棱和面的垂直关系,由此得到对应的面或者棱,并表示出来.
【详解详析】
利用“铅锤法”、“三角尺法”或者“合页型折纸法”可得知与棱DH垂直的面是面ABCD、面EFGH;与棱BC垂直的面是面ABFE、面DCGH;与棱AB垂直的面是面ADHE、面BCGF;与面ABCD垂直的棱有棱AE、棱BF、棱CG、棱DH;与面ABFE垂直的棱有棱AD、棱BC、棱FG、棱EH;与面BCGF垂直的棱有棱AB、棱CD、棱HG、棱EF;在长方体中的每一条棱有两个面和它垂直,每一个面有四条棱和它垂直.
故答案为:(1)面ABCD、面EFGH.
(2)面ABFE、面DCGH.
(3)面ADHE、面BCGF.
(4)棱AE、棱BF、棱CG、棱DH.
(5)棱AD、棱BC、棱FG、棱EH.
(6)棱AB、棱CD、棱HG、棱EF.
(7)两 四.
11. 棱CD 面DCGF 面ABCD 棱DF
【思路指引】
根据题意,利用长方体中棱与平面的位置关系来判断题目中棱与面的垂直关系.
【详解详析】
(1)与墙面ADFE垂直的墙角线是棱CD;
(2)与墙角线AD垂直的墙面是面DCGF;
(3)与墙角线DF垂直的墙面是面ABCD;
(4)与地面ABCD垂直的墙角线是棱DF.
故答案是:棱CD;面DCGF;面ABCD;棱DF.
12.棱、
【思路指引】
直接根据长方体中棱与平面的位置关系进行解答即可.
【详解详析】
如图所示:与平面平行的棱有棱、,
故答案为棱、.
13.(1)两,面EFGH、面CDHG;两,面ADHE、面EFGH;两,面BCGF、面CDHG;两;(2)四,棱EF、棱FG、棱GH、棱HE;四,棱BC、棱CG、棱GF、棱FB;四,棱CD、棱DH、棱HG、棱GC;四,(3)12对
【思路指引】
根据长方体棱与面之间的关系解答即可.
【详解详析】
(1)长方体中棱AB与两个面平行,分别是:面EFGH、面CDHG;
长方体中棱BC与两个面平行,分别是:面ADHE、面EFGH;
长方体中棱AE与两个面平行,分别是:面BCGF、面CDHG;
通过观察思考可以得到:长方体中每条棱都与两个面平行.
故答案为:两,面EFGH、面CDHG;两,面ADHE、面EFGH;两,面BCGF、面CDHG;两;
(2)长方体中面ABCD与四条棱平行,分别是:棱EF、棱FG、棱GH、棱HE;
长方体中面ADHE与四条棱平行,分别是:棱BC、棱CG、棱GF、棱FB;
长方体中面ABFE与四条棱平行,分别是:棱CD、棱DH、棱HG、棱GC;
通过观察思考可以得到:长方体中每个面都与四条棱平行;
故答案为:四,棱EF、棱FG、棱GH、棱HE;四,棱BC、棱CG、棱GF、棱FB;四,棱CD、棱DH、棱HG、棱GC;四;
(3)长方体中一共可以写出12对棱与面的平行关系.
如:棱AB与面EFGH;棱BC与面ADHE;棱CD与面ABFE;棱AD与面BCGF;棱EF与面ABCD;棱FG与面ADHE;棱GH与面ABCD;棱EH与面BCGF;棱AE与面BCGF;棱BF与面DCGH;棱CG与面ADHE;棱DH与面ABFE.
14.棱CD,棱DH,棱GH,棱CG,棱AD,棱DH,棱HE,棱EA,棱EF,棱AB,棱DC,棱HG
【思路指引】
根据长方体的特征,观察可得出结果.
【详解详析】
根据长方体的特征,与平面AEFB垂直的棱有棱棱CD,棱DH,棱GH,棱CG,
因此,若去掉长方体中的棱棱AD,棱DH,棱HE,棱EA,
则剩下的棱棱EF,棱AB,棱DC,棱HG都能与平面BFGC垂直,
故答案为:棱CD,棱DH,棱GH,棱CG,棱AD,棱DH,棱HE,棱EA,棱EF,棱AB,棱DC,棱HG.
15.4
【思路指引】
异面指不在同一个平面内,AD可看作在下面和左面两个平面内,只要不在下面和左面内的棱即可.
【详解详析】
解:棱AD异面的棱:BF、CG、EF、HG,
故答案为:4.
三、解答题
16.
解:如果把面ADHE和面ABFE组成的图形看作直立于面ABCD上的合页型折纸,那么可以说明棱AE⊥平面 ABCD.
∴图中可以用来检验AE垂直于面ABCD的现成的合页型折纸是面ADHE和面ABFE.
17.
(1)与棱AB垂直的面有两个:面CBGF、面ADHE;
(2)与面EFGH 垂直的棱有棱AE、棱BF、棱CG、棱DH.
18.
解:根据题意,
与平面DCEF垂直的棱有:棱FG、棱EH、棱CB、棱AD.共4条.
19.
解:把一个长方体切成两个长方体,只切一次,增加两个横截面,
所以只要增加的两个横截面的面积最大,则切成的表面积就最大,
所以应该按照高来切,平分成两个小长方体,切的横截面即为长×宽,
此时每一个小长方体的表面积为:2×(8×6)+2×(8×2)+2×(6×2)=96+32+24=152平面厘米,
故答案为:按照高来切,平分成两个小长方体;每个小长方体表面积为152平方厘米.
20.
(1)
如图,长方体ABCD﹣EFGH即为所求.
(2)
与棱FG平行的平面有平面ADHE,平面ABCD.
故答案为:平面ADHE,平面ABCD.
(3)
与平面HFBD垂直的平面有平面ABCD,平面EFGH.
故答案为:平面ABCD,平面EFGH.
