沪教版六年级数学下册8.5长方体中平面与平面的位置关系的认识 试题(含解析)
文档属性
| 名称 | 沪教版六年级数学下册8.5长方体中平面与平面的位置关系的认识 试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 328.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览




文档简介
8.5长方体中平面与平面的位置关系的认识
一、单选题
1.下列说法中,正确的有( )
①水平面就是一个平面;②长方体中相对的两个面不是平行就是垂直;③长方体中的每一条棱都会与两个面平行;④长方体中异面的棱共有24对;⑤长方体中与一个面垂直的棱有2条
A.2个 B.3个 C.4个 D.5个
2.下列说法中,不正确的是( )
A.用“长方形纸片”不可以检验直线与平面平行
B.用“三角尺”可以检验直线与平面垂直
C.用“铅垂线”可以检验直线与水平面平行
D.用“合页型折纸”可以检验平面与平面垂直
3.以下方法中并非用于检验直线与平面垂直的是( )
A.合页型折纸法 B.铅垂线法
C.长方形纸片法 D.三角尺法
4.以下表述中不正确的是( )
A.长方体中任何一条棱都与两个面平行
B.长方体中相对的两个面的面积相等
C.长方体中任何一个面都与四个面垂直
D.长方体中棱与棱不是相交就是异面
5.在长方体中,互相垂直的面有_______对,互相平行的面有________对.( )
A.3,1 B.4,2 C.9,3 D.12,3
6.在长方体中,下列说法错误的是( )
A.长方体中互相垂直的面共有12对 B.长方体中互相平行的面共有3对
C.长方体中相交的棱共有12对 D.长方体中异面的棱共有24对
7.在下列叙述中,正确的个数是( )
(1)两点之间线段最短;
(2)有理数分为正有理数和负有理数;
(3)一个锐角的补角是钝角;
(4)长方体中任何一个面都与两个面垂直.
A.1个 B.2个 C.3个 D.4个
8.下列叙述正确的个数是( )
①角的两边越长,角就越大;
②直线没有端点;
③长方体中任何一个面都与两个面垂直;
④长方体中棱与棱不平行就相交.
A.1 B.2 C.3 D.4
9.将棱长为的正方体表面涂上红色切成边长为的小正方体后,一面是红色的小正方体有( )
A.256个 B.992个 C.384个 D.880个
10.下列说法中,错误的是( )
A.长方体中相对的两个面的面积相等
B.长方体中任何一条棱都与两个面平行
C.长方体中棱与棱不是相交就是平行
D.长方体中任何一个面都与四个面垂直
二、填空题
11.长方体的长、宽、高之比是,棱长的总和是80厘米,把这个长方体截成两个正方体时,表面积增加了_______平方厘米.
12.如图所示,它是一个正方体六个面的展开图,那么原正方体中与平面互相平行的平面是_______.(用图中字母表示)
13.对长方体如图所示那样截去一角后余下的几何体有________个顶点、_______条棱、_______个面.
14.将6个棱长为1厘米的正方体拼成一个长方体,则表面积减少了_______平方厘米.
15.一个教室长8米,宽5米,高4米,要粉刷教室的顶面和四周墙壁,除去门窗面积21.5平方米,粉刷面积是_______平方米,如果每平方米用油漆0.25千克,共要用油漆_______千克.
16.如果把骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,则与点数是3的面垂直的所有的面的点数和是_______.
17.一个无盖的长方体木盒,棱长分别为、和,则它的外表面积是_______.
18.将一个棱长为的正方体任意截成两个长方体,这两个长方体表面积的和是_______.
19.一块长方体的木块,从左面和右面分别裁去长为2厘米和5厘米的长方体,成为一个正方体后,表面积减少了84平方厘米,那么原来长方体的体积为_______.
20.如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的_______.(填序号)
三、解答题
21.观察下列图中由棱长为1的小立方体摆成的图形,寻找规律:
如图①:共有1个小立方体,其中1个看得见,0个看不见.
(1)如图②:共有8个小立方体,其中________个看得见,_______个看不见.
(2)如图③:共有_______个小立方体,其中________个看得见,_______个看不见.
(3)按此规律在第⑥个图中,看不见的小立方体有多少个?
22.如图所示,长方体中,从点出发的三条棱、、的长度比为,该长方体的棱长总和为144厘米,求与面垂直的各个面的面积之和.
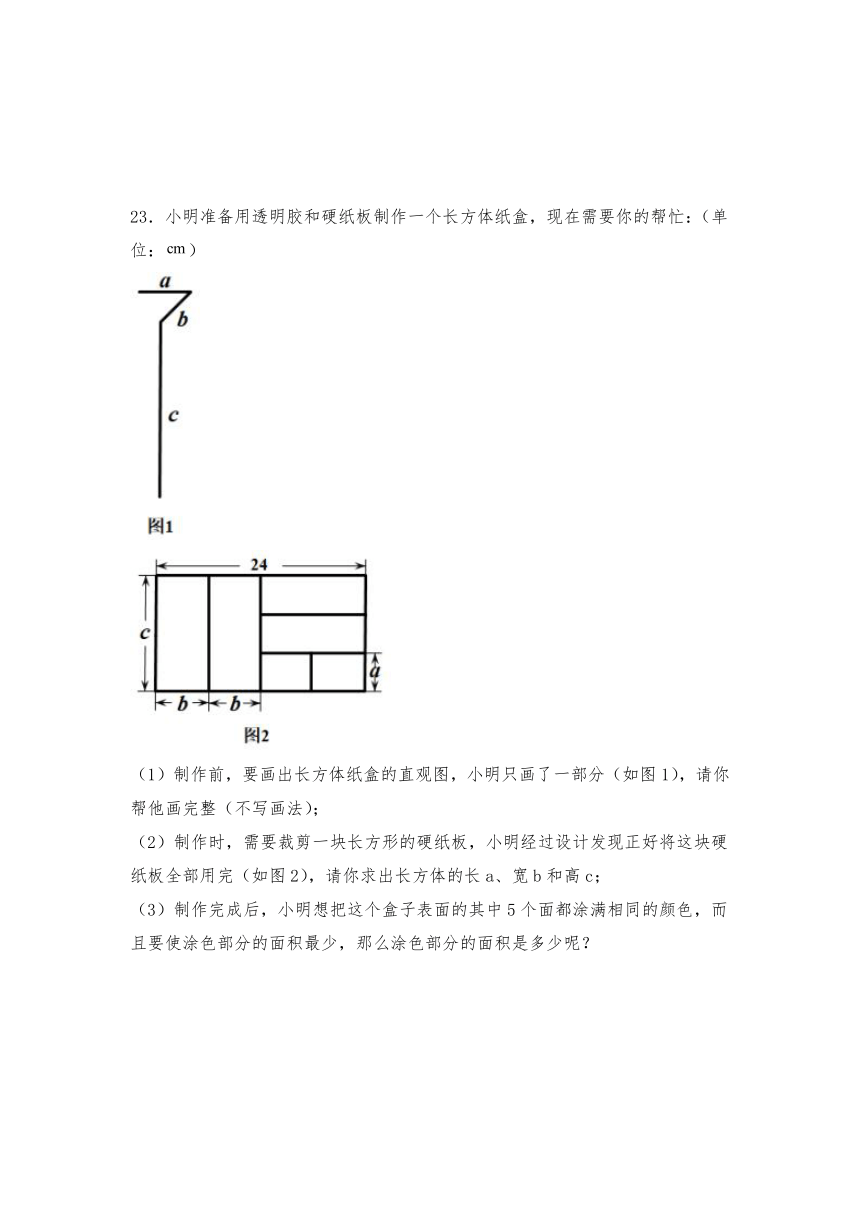
23.小明准备用透明胶和硬纸板制作一个长方体纸盒,现在需要你的帮忙:(单位:)
(1)制作前,要画出长方体纸盒的直观图,小明只画了一部分(如图1),请你帮他画完整(不写画法);
(2)制作时,需要裁剪一块长方形的硬纸板,小明经过设计发现正好将这块硬纸板全部用完(如图2),请你求出长方体的长a、宽b和高c;
(3)制作完成后,小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少,那么涂色部分的面积是多少呢?
24.将棱长为3厘米的正方体木块表面涂成红色,切割成棱长为1厘米的小正方体,分别求出三面红色、两面红色和没有红色的小正方体的数量.
25.如图所示是一个透明的长方体容器,里面装着水,从里面量长、宽、高分别是16厘米、4厘米、8厘米,水深6厘米.如果把长方体的左侧面作为底面,放在桌子上,那么水深多少厘米?
答案
一、单选题
1.B
【思路指引】
根据长方体的特征逐一判断即可.
【详解详析】
①水平面就是一个平面,故正确;
②长方体中相对的两个面不是平行就是垂直,故错误;
③长方体中的每一条棱都会与两个面平行,故正确;
④长方体中异面的棱共有24对,故正确;
⑤长方体中与一个面垂直的棱有2条,故错误;
故选:B.
2.A
【思路指引】
根据直线与平面位置关系的检验方法逐一分析即可.
【详解详析】
A.根据长方形的对边平行,所以用“长方形纸片”可以检验直线与平面平行,故A不正确;
B.利用“三角尺”中的直角可以检验直线与平面垂直,故B正确;
C. 根据重力学原理,铅垂线垂直于水平面,与铅垂线垂直的直线则与平面平行,故C正确;
D. “合页型折纸”其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把折断的两边放到平面上,可判断折痕与水平面垂直,从而检验平面与平面垂直,故D正确.
故选A.
3.C
【思路指引】
检验直线与平面垂直的方法:若该直线与该平面内的两条相交直线垂直,则该直线与该平面垂直;若该直线与该平面中的任意一条直线垂直,则该直线与该平面垂直;若该直线平行于垂直该平面的另一个平面,则该直线与该平面垂直;根据直线与平面的判定方法逐一判断即可.
【详解详析】
A项,如图1,合页型折纸其痕迹与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把两放到水平面上,可判断折痕与水平面垂直,A不符合题意;
B项,如图2,根据重力学原理,铅垂线垂直水平面,B不符合题意;
C项,长方形纸片只能判定长与宽相互垂直,不能判断与水平面垂直,C符合题意;
D项,将两块三角板的直角边重合,另外两条直角边相交,放在水平面上,可判断重合的直角边垂直于水平面,D不符合题意;
故选C.
4.D
【思路指引】
根据长方体中棱与面的关系判断即可;
【详解详析】
长方体中任何一条棱都与两个面平行,正确;
长方体中相对的两个面的面积相等,正确;
长方体中任何一个面都与四个面垂直,正确;
长方体中棱与棱不是相交就是异面,不正确;
故答案选D.
5.D
【思路指引】
在立方体中,面与面之间的关系有平行和垂直两种.
【详解详析】
解:和平面ABCD相交的平面与平面ABCD垂直,有4个;和平面EFGH相交的平面且垂直的,有4个;四个侧面两两互相垂直,有4个;4×3=12(对).
长方体的六个面中,互相平行的面即相对的两个面是互相平行的,所以共有3对互相平行的面.
故选:D.
6.C
【思路指引】
直接根据长方体中棱、面之间的位置关系进行排除即可.
【详解详析】
A、长方体中互相垂直的面共有12对,故正确;
B、长方体中互相平行的面共有3对,故正确;
C、长方体中相交的棱共有24对,故错误;
D、长方体中异面的棱共有24对,故正确.
故选C.
7.B
【思路指引】
依据有理数的分类、线段的性质、补角的定义、根据长方体六个面的关系,即可得到正确结论.
【详解详析】
解:(1)两点之间,线段最短,故本选项正确;
(2)有理数分为正有理数和负有理数以及零,故本选项错误;
(3)一个锐角的补角是钝角,故本选项正确;
(4)长方体中任何一个面都与4个面垂直,所以本选项不正确.
正确的个数是2个,
故选:B.
8.A
【思路指引】
根据角的大小与角的两边的长短无关,直线的特征,长方体的认识,逐项判断即可求解.
【详解详析】
解:角的大小与角的两边的长短无关,故①错误,不符合题意;
直线没有端点,是可以无限延伸的,故②正确,符合题意;
长方体中任何一个面都与4个面垂直,故③错误,不符合题意;
长方体中棱与棱不平行就相交、还有异面,故④错误,不符合题意;
所以正确的有1个.
故选:A
9.C
【思路指引】
根据题意分析出三面涂色、两面涂色、没有涂色的小正方体的个数,然后进行求解即可.
【详解详析】
解:小正方体个数:(个),根据题意可发现顶点处的小正方体三面涂色,除顶点外位于棱上的小正方体两面涂色,而处于正中心的则没徐色,则一面红色的有:(个).
故选C .
10.C
【思路指引】
根据长方体中面与面、棱与棱的位置关系逐项判断即可得.
【详解详析】
A、长方体中相对的两个面的面积相等,此项说法正确;
B、长方体中任何一条棱都与两个面平行,此项说法正确;
C、长方体中棱与棱的位置关系有相交、平行、异面,此项说法错误;
D、长方体中任何一个面都与四个面垂直,此项说法正确;
故选:C.
二、填空题
11.50
【思路指引】
根据题意易得长方体的长宽高,然后可直接进行求解.
【详解详析】
解:设长为厘米,则高与宽都为厘米,由题意得:
,得(厘米),
长方体截成两个正方体,增加了两个正方形的面积,即(平方厘米).
故答案为50.
12.平面
【思路指引】
只需要找出平面B的对面即可;
【详解详析】
根据题意可知:平面B的相对面是平面D,所以平面D与平面B平行;
故答案是平面D.
13. 7 12 7
【思路指引】
根据截一个立体图形的知识点判断即可;
【详解详析】
根据图形可得截去一角后余下的几何体有7个顶点、12条棱、7个面.
故答案是:7,12,7.
14.10或14
【思路指引】
根据题意可得拼接方法有两种:一种是,一种是,然后进行分类求解即可.
【详解详析】
解:①如果是的拼法,拼法之前是(平方厘米),拼之后是(平方厘米),减少了14平方厘米,
②如果是的拼法,拼之前是36平方厘米,拼之后是(平方厘米),减少了10平方厘米.
故答案为10或14.
15. 122.5 30.625
【思路指引】
根据题意直接列式计算求解即可.
【详解详析】
解:由题意得:
粉刷面积:(平方米),
共用油漆:(千克).
故答案为122.5,30.625.
16.14
【思路指引】
根据正方体中面与面的位置关系知道除了点数是4的面,其他的面都与点数是3的面垂直.
【详解详析】
解:与点数是3的面垂直的所有的面的点数和是.
故答案是:14.
17.143,134或118
【思路指引】
根据题意可直接得到长方体的表面积有三种可能,然后分别求解即可.
【详解详析】
解:①以为底面的长方体木盒的表面积
②以为底面的长方体木盒的表面积:.
③以为底面的长方体木盒的表面积:.
故答案为143,134,118.
18.
【思路指引】
将一个棱长为的正方体任意截成两个长方体,对比原棱长为的正方体的面积,找到多出来的部分,通过计算即可得到答案.
【详解详析】
将一个棱长为的正方体任意截成两个长方体,
则:任意截成两个长方体表面积之和=原正方体表面积之和+原正方体的两个面的面积;
∵原棱长为的正方体总共有6个面
又∵一个棱长为的正方体,每个面的面积为:
∴任意截成两个长方体表面积之和=
故答案为:.
19.90立方厘米
【思路指引】
设正方体棱长为厘米,根据题意列方程可求得x的值,进而得到原长方体的长、宽、高的值,再计算体积即可.
【详解详析】
设正方体棱长为厘米,
依题意得,
解得,
则原长方体的宽为3厘米,高为3厘米,长为厘米,
则立方厘米.
20.②⑤
【思路指引】
结合题意,根据简单几何体展开图的性质对各个选项逐个分析,即可得到答案.
【详解详析】
根据题意,再剪开一条棱,展开图不可能为:
故答案为:②⑤.
三、解答题
21.
解:第①幅图,即,共有小立方体的个数是1,看不见的小立方体的个数是0,看得见的小立方体是(个);
(1)第②幅图,即时,共有小立方体(个),看不见的小立方体的个数是,看得见的小立方体的个数是;
故答案为7;1;
(2)第③幅图,即时,共有小立方体(个),看不见的小立方体的个数是(个),看得见小立方体的个数是(个);
故答案为27,19,8;
(3)第⑥幅图,即时,共有小立方体的个数为(个);看不见的小立方体的个数为.
答:看不见的小立方体有125个.
22.
解:设棱、、的长度为厘米、厘米、厘米,由题意得:
∴,,
∴棱、、的长度分别为6厘米、12厘米、18厘米,
则与面垂直的面为面、面、面、面,面积之和为(平方厘米).
23.
(1)见下图
(2)由图2可知:
∴
∵
∴
∵
∴
∴cm,cm,cm.
(3)∵小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少
∴边长为6cm和12cm的两个面中的一个面不涂色
∴cm2.
24.
解:由题意得:
因为(个),所以大正方体每条棱长上面都有3个小正方体;
三面涂色的在8个顶点处,所以一共有8个;
两面都涂有红色,在除了顶点外的棱上:
(个);
一面涂色的在大正方体的6个面上,共(个);
没有涂色的在第二层正中间,只有1个.
答:三面涂色的小正方体有8个,两面涂色的有12个,没有涂色的只有1个.
25.
解:由题意得:
水量一定,水的体积为(立方厘米),左侧面的面积为(平方厘米),水深为(厘米).
答:水深为12厘米.
一、单选题
1.下列说法中,正确的有( )
①水平面就是一个平面;②长方体中相对的两个面不是平行就是垂直;③长方体中的每一条棱都会与两个面平行;④长方体中异面的棱共有24对;⑤长方体中与一个面垂直的棱有2条
A.2个 B.3个 C.4个 D.5个
2.下列说法中,不正确的是( )
A.用“长方形纸片”不可以检验直线与平面平行
B.用“三角尺”可以检验直线与平面垂直
C.用“铅垂线”可以检验直线与水平面平行
D.用“合页型折纸”可以检验平面与平面垂直
3.以下方法中并非用于检验直线与平面垂直的是( )
A.合页型折纸法 B.铅垂线法
C.长方形纸片法 D.三角尺法
4.以下表述中不正确的是( )
A.长方体中任何一条棱都与两个面平行
B.长方体中相对的两个面的面积相等
C.长方体中任何一个面都与四个面垂直
D.长方体中棱与棱不是相交就是异面
5.在长方体中,互相垂直的面有_______对,互相平行的面有________对.( )
A.3,1 B.4,2 C.9,3 D.12,3
6.在长方体中,下列说法错误的是( )
A.长方体中互相垂直的面共有12对 B.长方体中互相平行的面共有3对
C.长方体中相交的棱共有12对 D.长方体中异面的棱共有24对
7.在下列叙述中,正确的个数是( )
(1)两点之间线段最短;
(2)有理数分为正有理数和负有理数;
(3)一个锐角的补角是钝角;
(4)长方体中任何一个面都与两个面垂直.
A.1个 B.2个 C.3个 D.4个
8.下列叙述正确的个数是( )
①角的两边越长,角就越大;
②直线没有端点;
③长方体中任何一个面都与两个面垂直;
④长方体中棱与棱不平行就相交.
A.1 B.2 C.3 D.4
9.将棱长为的正方体表面涂上红色切成边长为的小正方体后,一面是红色的小正方体有( )
A.256个 B.992个 C.384个 D.880个
10.下列说法中,错误的是( )
A.长方体中相对的两个面的面积相等
B.长方体中任何一条棱都与两个面平行
C.长方体中棱与棱不是相交就是平行
D.长方体中任何一个面都与四个面垂直
二、填空题
11.长方体的长、宽、高之比是,棱长的总和是80厘米,把这个长方体截成两个正方体时,表面积增加了_______平方厘米.
12.如图所示,它是一个正方体六个面的展开图,那么原正方体中与平面互相平行的平面是_______.(用图中字母表示)
13.对长方体如图所示那样截去一角后余下的几何体有________个顶点、_______条棱、_______个面.
14.将6个棱长为1厘米的正方体拼成一个长方体,则表面积减少了_______平方厘米.
15.一个教室长8米,宽5米,高4米,要粉刷教室的顶面和四周墙壁,除去门窗面积21.5平方米,粉刷面积是_______平方米,如果每平方米用油漆0.25千克,共要用油漆_______千克.
16.如果把骰子看作是一个正方体,点数1的对面是6,点数5的对面是2,点数4的对面是3,则与点数是3的面垂直的所有的面的点数和是_______.
17.一个无盖的长方体木盒,棱长分别为、和,则它的外表面积是_______.
18.将一个棱长为的正方体任意截成两个长方体,这两个长方体表面积的和是_______.
19.一块长方体的木块,从左面和右面分别裁去长为2厘米和5厘米的长方体,成为一个正方体后,表面积减少了84平方厘米,那么原来长方体的体积为_______.
20.如图是一个没有完全剪开的正方体,若再剪开一条棱,则得到的平面展开图不可能是下列图中的_______.(填序号)
三、解答题
21.观察下列图中由棱长为1的小立方体摆成的图形,寻找规律:
如图①:共有1个小立方体,其中1个看得见,0个看不见.
(1)如图②:共有8个小立方体,其中________个看得见,_______个看不见.
(2)如图③:共有_______个小立方体,其中________个看得见,_______个看不见.
(3)按此规律在第⑥个图中,看不见的小立方体有多少个?
22.如图所示,长方体中,从点出发的三条棱、、的长度比为,该长方体的棱长总和为144厘米,求与面垂直的各个面的面积之和.
23.小明准备用透明胶和硬纸板制作一个长方体纸盒,现在需要你的帮忙:(单位:)
(1)制作前,要画出长方体纸盒的直观图,小明只画了一部分(如图1),请你帮他画完整(不写画法);
(2)制作时,需要裁剪一块长方形的硬纸板,小明经过设计发现正好将这块硬纸板全部用完(如图2),请你求出长方体的长a、宽b和高c;
(3)制作完成后,小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少,那么涂色部分的面积是多少呢?
24.将棱长为3厘米的正方体木块表面涂成红色,切割成棱长为1厘米的小正方体,分别求出三面红色、两面红色和没有红色的小正方体的数量.
25.如图所示是一个透明的长方体容器,里面装着水,从里面量长、宽、高分别是16厘米、4厘米、8厘米,水深6厘米.如果把长方体的左侧面作为底面,放在桌子上,那么水深多少厘米?
答案
一、单选题
1.B
【思路指引】
根据长方体的特征逐一判断即可.
【详解详析】
①水平面就是一个平面,故正确;
②长方体中相对的两个面不是平行就是垂直,故错误;
③长方体中的每一条棱都会与两个面平行,故正确;
④长方体中异面的棱共有24对,故正确;
⑤长方体中与一个面垂直的棱有2条,故错误;
故选:B.
2.A
【思路指引】
根据直线与平面位置关系的检验方法逐一分析即可.
【详解详析】
A.根据长方形的对边平行,所以用“长方形纸片”可以检验直线与平面平行,故A不正确;
B.利用“三角尺”中的直角可以检验直线与平面垂直,故B正确;
C. 根据重力学原理,铅垂线垂直于水平面,与铅垂线垂直的直线则与平面平行,故C正确;
D. “合页型折纸”其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把折断的两边放到平面上,可判断折痕与水平面垂直,从而检验平面与平面垂直,故D正确.
故选A.
3.C
【思路指引】
检验直线与平面垂直的方法:若该直线与该平面内的两条相交直线垂直,则该直线与该平面垂直;若该直线与该平面中的任意一条直线垂直,则该直线与该平面垂直;若该直线平行于垂直该平面的另一个平面,则该直线与该平面垂直;根据直线与平面的判定方法逐一判断即可.
【详解详析】
A项,如图1,合页型折纸其痕迹与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把两放到水平面上,可判断折痕与水平面垂直,A不符合题意;
B项,如图2,根据重力学原理,铅垂线垂直水平面,B不符合题意;
C项,长方形纸片只能判定长与宽相互垂直,不能判断与水平面垂直,C符合题意;
D项,将两块三角板的直角边重合,另外两条直角边相交,放在水平面上,可判断重合的直角边垂直于水平面,D不符合题意;
故选C.
4.D
【思路指引】
根据长方体中棱与面的关系判断即可;
【详解详析】
长方体中任何一条棱都与两个面平行,正确;
长方体中相对的两个面的面积相等,正确;
长方体中任何一个面都与四个面垂直,正确;
长方体中棱与棱不是相交就是异面,不正确;
故答案选D.
5.D
【思路指引】
在立方体中,面与面之间的关系有平行和垂直两种.
【详解详析】
解:和平面ABCD相交的平面与平面ABCD垂直,有4个;和平面EFGH相交的平面且垂直的,有4个;四个侧面两两互相垂直,有4个;4×3=12(对).
长方体的六个面中,互相平行的面即相对的两个面是互相平行的,所以共有3对互相平行的面.
故选:D.
6.C
【思路指引】
直接根据长方体中棱、面之间的位置关系进行排除即可.
【详解详析】
A、长方体中互相垂直的面共有12对,故正确;
B、长方体中互相平行的面共有3对,故正确;
C、长方体中相交的棱共有24对,故错误;
D、长方体中异面的棱共有24对,故正确.
故选C.
7.B
【思路指引】
依据有理数的分类、线段的性质、补角的定义、根据长方体六个面的关系,即可得到正确结论.
【详解详析】
解:(1)两点之间,线段最短,故本选项正确;
(2)有理数分为正有理数和负有理数以及零,故本选项错误;
(3)一个锐角的补角是钝角,故本选项正确;
(4)长方体中任何一个面都与4个面垂直,所以本选项不正确.
正确的个数是2个,
故选:B.
8.A
【思路指引】
根据角的大小与角的两边的长短无关,直线的特征,长方体的认识,逐项判断即可求解.
【详解详析】
解:角的大小与角的两边的长短无关,故①错误,不符合题意;
直线没有端点,是可以无限延伸的,故②正确,符合题意;
长方体中任何一个面都与4个面垂直,故③错误,不符合题意;
长方体中棱与棱不平行就相交、还有异面,故④错误,不符合题意;
所以正确的有1个.
故选:A
9.C
【思路指引】
根据题意分析出三面涂色、两面涂色、没有涂色的小正方体的个数,然后进行求解即可.
【详解详析】
解:小正方体个数:(个),根据题意可发现顶点处的小正方体三面涂色,除顶点外位于棱上的小正方体两面涂色,而处于正中心的则没徐色,则一面红色的有:(个).
故选C .
10.C
【思路指引】
根据长方体中面与面、棱与棱的位置关系逐项判断即可得.
【详解详析】
A、长方体中相对的两个面的面积相等,此项说法正确;
B、长方体中任何一条棱都与两个面平行,此项说法正确;
C、长方体中棱与棱的位置关系有相交、平行、异面,此项说法错误;
D、长方体中任何一个面都与四个面垂直,此项说法正确;
故选:C.
二、填空题
11.50
【思路指引】
根据题意易得长方体的长宽高,然后可直接进行求解.
【详解详析】
解:设长为厘米,则高与宽都为厘米,由题意得:
,得(厘米),
长方体截成两个正方体,增加了两个正方形的面积,即(平方厘米).
故答案为50.
12.平面
【思路指引】
只需要找出平面B的对面即可;
【详解详析】
根据题意可知:平面B的相对面是平面D,所以平面D与平面B平行;
故答案是平面D.
13. 7 12 7
【思路指引】
根据截一个立体图形的知识点判断即可;
【详解详析】
根据图形可得截去一角后余下的几何体有7个顶点、12条棱、7个面.
故答案是:7,12,7.
14.10或14
【思路指引】
根据题意可得拼接方法有两种:一种是,一种是,然后进行分类求解即可.
【详解详析】
解:①如果是的拼法,拼法之前是(平方厘米),拼之后是(平方厘米),减少了14平方厘米,
②如果是的拼法,拼之前是36平方厘米,拼之后是(平方厘米),减少了10平方厘米.
故答案为10或14.
15. 122.5 30.625
【思路指引】
根据题意直接列式计算求解即可.
【详解详析】
解:由题意得:
粉刷面积:(平方米),
共用油漆:(千克).
故答案为122.5,30.625.
16.14
【思路指引】
根据正方体中面与面的位置关系知道除了点数是4的面,其他的面都与点数是3的面垂直.
【详解详析】
解:与点数是3的面垂直的所有的面的点数和是.
故答案是:14.
17.143,134或118
【思路指引】
根据题意可直接得到长方体的表面积有三种可能,然后分别求解即可.
【详解详析】
解:①以为底面的长方体木盒的表面积
②以为底面的长方体木盒的表面积:.
③以为底面的长方体木盒的表面积:.
故答案为143,134,118.
18.
【思路指引】
将一个棱长为的正方体任意截成两个长方体,对比原棱长为的正方体的面积,找到多出来的部分,通过计算即可得到答案.
【详解详析】
将一个棱长为的正方体任意截成两个长方体,
则:任意截成两个长方体表面积之和=原正方体表面积之和+原正方体的两个面的面积;
∵原棱长为的正方体总共有6个面
又∵一个棱长为的正方体,每个面的面积为:
∴任意截成两个长方体表面积之和=
故答案为:.
19.90立方厘米
【思路指引】
设正方体棱长为厘米,根据题意列方程可求得x的值,进而得到原长方体的长、宽、高的值,再计算体积即可.
【详解详析】
设正方体棱长为厘米,
依题意得,
解得,
则原长方体的宽为3厘米,高为3厘米,长为厘米,
则立方厘米.
20.②⑤
【思路指引】
结合题意,根据简单几何体展开图的性质对各个选项逐个分析,即可得到答案.
【详解详析】
根据题意,再剪开一条棱,展开图不可能为:
故答案为:②⑤.
三、解答题
21.
解:第①幅图,即,共有小立方体的个数是1,看不见的小立方体的个数是0,看得见的小立方体是(个);
(1)第②幅图,即时,共有小立方体(个),看不见的小立方体的个数是,看得见的小立方体的个数是;
故答案为7;1;
(2)第③幅图,即时,共有小立方体(个),看不见的小立方体的个数是(个),看得见小立方体的个数是(个);
故答案为27,19,8;
(3)第⑥幅图,即时,共有小立方体的个数为(个);看不见的小立方体的个数为.
答:看不见的小立方体有125个.
22.
解:设棱、、的长度为厘米、厘米、厘米,由题意得:
∴,,
∴棱、、的长度分别为6厘米、12厘米、18厘米,
则与面垂直的面为面、面、面、面,面积之和为(平方厘米).
23.
(1)见下图
(2)由图2可知:
∴
∵
∴
∵
∴
∴cm,cm,cm.
(3)∵小明想把这个盒子表面的其中5个面都涂满相同的颜色,而且要使涂色部分的面积最少
∴边长为6cm和12cm的两个面中的一个面不涂色
∴cm2.
24.
解:由题意得:
因为(个),所以大正方体每条棱长上面都有3个小正方体;
三面涂色的在8个顶点处,所以一共有8个;
两面都涂有红色,在除了顶点外的棱上:
(个);
一面涂色的在大正方体的6个面上,共(个);
没有涂色的在第二层正中间,只有1个.
答:三面涂色的小正方体有8个,两面涂色的有12个,没有涂色的只有1个.
25.
解:由题意得:
水量一定,水的体积为(立方厘米),左侧面的面积为(平方厘米),水深为(厘米).
答:水深为12厘米.
