沪教版七年级数学下册 第十五章 平面直角坐标系 基础过关测试卷 (含解析)
文档属性
| 名称 | 沪教版七年级数学下册 第十五章 平面直角坐标系 基础过关测试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 14:29:01 | ||
图片预览



文档简介
第十五章 《平面直角坐标系》(基础过关测试卷)
一、选择题(每小题4分,共24分)
1.如果点A(3,m)在x轴上,那么点B(m+2,m﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P的横坐标是﹣3,且到x轴的距离为5,则P点的坐标是( )
A.(5,﹣3)或(﹣5,﹣3) B.(﹣3,5)或(﹣3,﹣5)
C.(﹣3,5) D.(﹣3,﹣5)
3.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A.﹣1 B.1 C.5 D.﹣5
4.如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
(﹣3,2) B.(﹣1,﹣3) C.(﹣1,﹣2) D.(0,﹣2)
5.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A,C的坐标分别是(6,0),(0,3),点B在第一象限,则点B的坐标是( )
(3,6) B.(6,3) C.(6,6) D.(3,3)
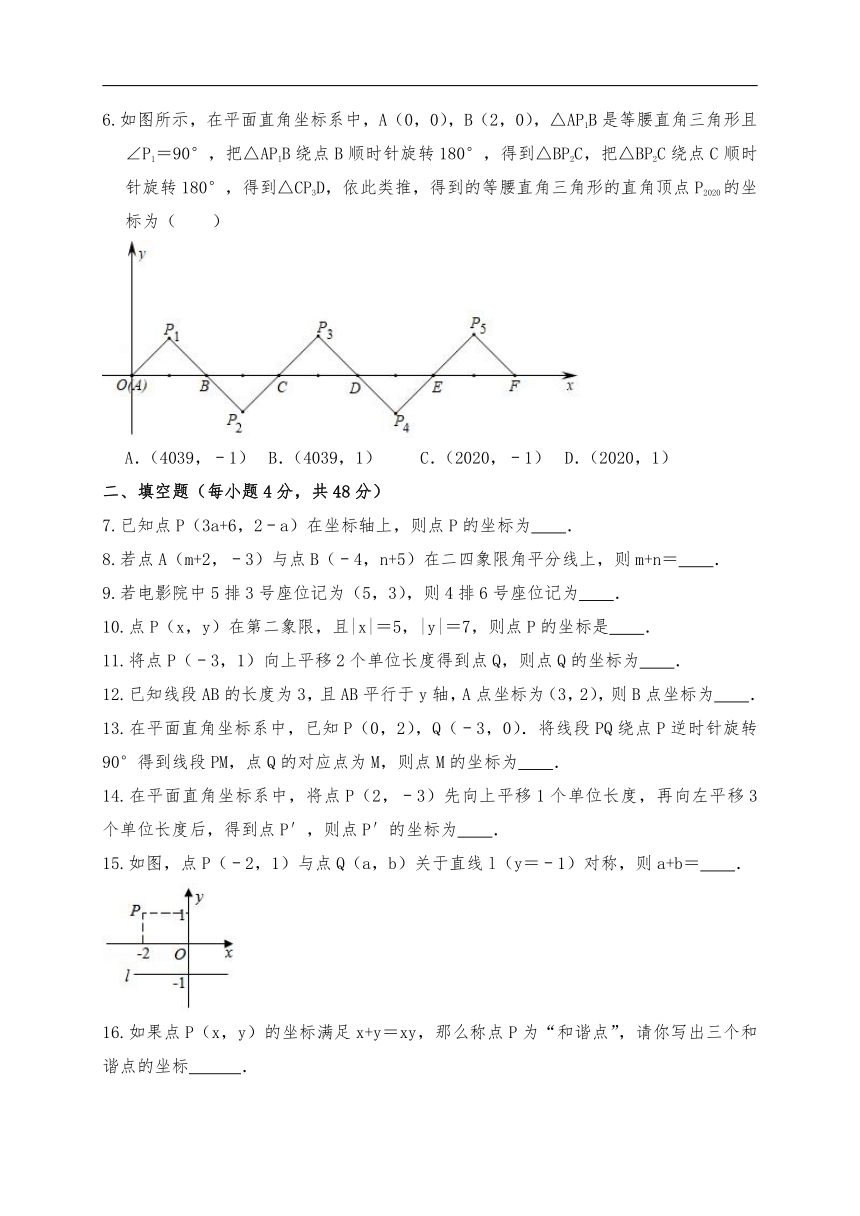
6.如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
A.(4039,﹣1) B.(4039,1) C.(2020,﹣1) D.(2020,1)
二、填空题(每小题4分,共48分)
7.已知点P(3a+6,2﹣a)在坐标轴上,则点P的坐标为 .
8.若点A(m+2,﹣3)与点B(﹣4,n+5)在二四象限角平分线上,则m+n= .
9.若电影院中5排3号座位记为(5,3),则4排6号座位记为 .
10.点P(x,y)在第二象限,且|x|=5,|y|=7,则点P的坐标是 .
11.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.已知线段AB的长度为3,且AB平行于y轴,A点坐标为(3,2),则B点坐标为 .
13.在平面直角坐标系中,已知P(0,2),Q(﹣3,0).将线段PQ绕点P逆时针旋转90°得到线段PM,点Q的对应点为M,则点M的坐标为 .
14.在平面直角坐标系中,将点P(2,﹣3)先向上平移1个单位长度,再向左平移3个单位长度后,得到点P′,则点P′的坐标为 .
15.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= .
16.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,请你写出三个和谐点的坐标 .
17.已知点A(a,2019)与点B(2020,b)关于y轴对称,则a+b的值为 .
18.教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,若两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),例如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4)请利用以上结论解决问题:在平面直角坐标系中,若点E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于x轴上,且到y轴的距离是2,则2a+b的值等于 .
三、解答题(共78分)
19.(8分)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2019的值.
20.(10分)在平面直角坐标系中,已知点M(m﹣1,2m+3).
(1)若点M在y轴上,求m的值.
(2)若点N(﹣3,2),且直线MN∥y轴,求线段MN的长.
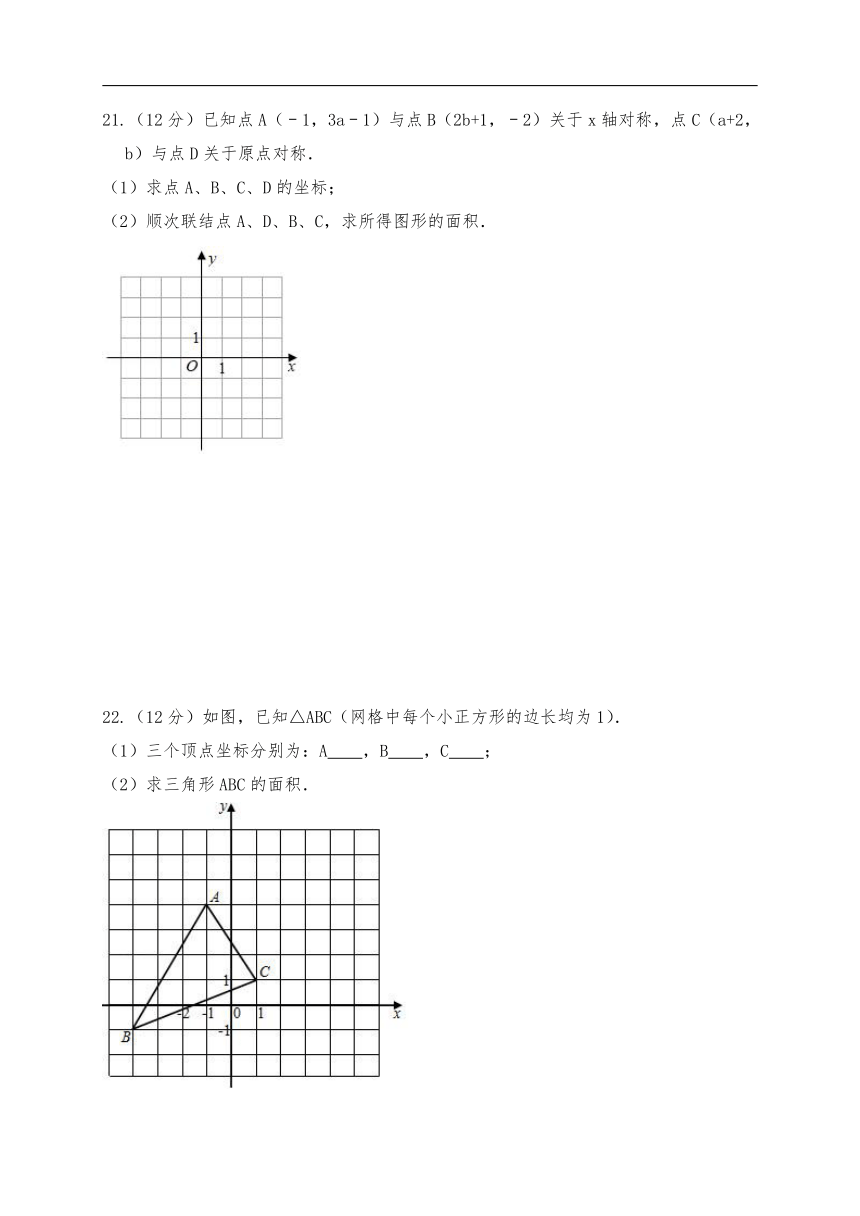
21.(12分)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
22.(12分)如图,已知△ABC(网格中每个小正方形的边长均为1).
(1)三个顶点坐标分别为:A ,B ,C ;
(2)求三角形ABC的面积.
23.(12分)已知点A(a﹣5,1﹣2a),解答下列问题:
(1)若点A到x轴和y轴的距离相等,求点A的坐标;
(2)若点A向右平移若干个单位后,与点B(﹣2,﹣3)关于x轴对称,求点A的坐标.
24.(12分)如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
25.(12分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为 ;
(2)若点P的“5级关联点”的坐标为(9,﹣3),求点P的坐标;
(3)若点P(m﹣1,2m)的“﹣3级关联点”P′位于坐标轴上.求点P′的坐标.
答案
一、选择题
1.D
【分析】根据x轴上的点的纵坐标为0列式求出m的值,然后计算即可得解.
【解答】解:∵A(3,m)在x轴上,
∴m=0,
∴m+2=2,m﹣3=﹣3,
∴B(m+2,m﹣3)所在的象限是第四象限.
故选:D.
2.B
【分析】点P到x轴的距离为5即P点的纵坐标是5或﹣5,又因为点P的横坐标是﹣3,即可得P点坐标.
【解答】解:∵点P到x轴的距离为5,
∴P点的纵坐标是5或﹣5,
∵点P的横坐标是﹣3,
∴P点的坐标是(﹣3,5)或(﹣3,﹣5).
故选:B.
3.B
【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得x、y的值,根据有理数的加法,可得答案.
【解答】解:由P(x、y)在第二象限且|x|=2,|y|=3,得
x=﹣2,y=3.
x+y=﹣2+3=1,
故选:B.
4.C
【分析】利用平移变换的性质解决问题即可.
【解答】解:观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
5.B
【分析】根据矩形的性质得出点B的坐标即可.
【解答】解:∵四边形OABC是矩形,
∴OC=AB,CB=OA,
∵点A,C的坐标分别是(6,0),(0,3),
∴AB=3,OA=6,
∴点B坐标为(6,3),
故选:B.
6.A
【分析】根据等腰直角三角形的性质可找出点P1的坐标,结合旋转的性质即可找出点P2、P3、P4、P5、…、的坐标,根据坐标的变化即可找出变化规律“P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数)”,依此规律即可得出结论.
【解答】解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,
∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,
∴P2(3,﹣1).
同理可得出:P3(5,1),P4(7,﹣1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数).
∵2020=2×1009+2,4×1009+3=4039,
∴P2020(4039,﹣1).
故选:A.
二、填空题
7.(12,0)或(0,4)
【分析】分点P在x轴上,纵坐标为0;在y轴上,横坐标为0,分别列式求出a的值,再求解即可.
【解答】解:当P在x轴上时,2﹣a=0,
解得:a=2,
则3a+6=12,
故P(12,0);
当P在y轴上时,3a+6=0,
解得:a=﹣2,
故2﹣a=4,
则P(0,4).
所以P(12,0)或(0,4).
故答案为:(12,0)或(0,4).
8.0
【分析】由点A(m+2,﹣3)与点B(﹣4,n+5)在二四象限的角平分线上可得m+2与﹣3互为相反数,﹣4与n+5互为相反,从而可求得m,n的值,从而求得m+n的值.
【解答】解:∵A(m+2,﹣3)在二四象限角平分线上,
∴m+2=3,
解得m=1,
∵点B(﹣4,n+5)在二四象限角平分线上,
∴n+5=4,
解得n=﹣1,
∴m+n=1﹣1=0.
故答案为:0.
9.(4,6)
【分析】明确对应关系,排在前,号在后,然后解答.
【解答】解:电影院中的5排3号记为(5,3),
则4排6号记为(4,6).
故答案为:(4,6).
10.(-5,7)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数结合绝对值的性质求出x、y的值,然后写出即可.
【解答】解:∵点P(x,y)在第二象限,且|x|=5,|y|=7,
∴x=﹣5,y=7,
∴点P的坐标为(﹣5,7).
故答案为:(﹣5,7).
11.(-3,3)
【分析】根据向上平移,横坐标不变,纵坐标加可得结论.
【解答】解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
12.(3,-1)或(3,5)
【分析】由AB∥y轴可得A,B两点的横坐标相同,结合AB=3,A(3,2),分B点在A点之上和之下两种情况可求解B点的纵坐标,进而可求解.
【解答】解:∵AB∥y轴,
∴A,B两点的横坐标相同,
∵A(3,2),
∴B点横坐标为3,
∵AB=3,
∴当B点在A点之上时,B点纵坐标为2+3=5,
∴B(3,5);
∴当B点在A点之下时,B点纵坐标为2﹣3=﹣1,
∴B(3,﹣1).
综上B点坐标为(3,﹣1)或(3,5).
故答案为(3,﹣1)或(3,5).
13.(2,-1)
【分析】利用旋转变换的性质作出图形即可解决问题.
【解答】解:如图,由作图可知,M(2,﹣1).
故答案为(2,﹣1).
14.(-1,-2)
【分析】根据平移规律:横坐标右移加,左移减;纵坐标上移加,下移减即可得.
【解答】解:平移后点Q的坐标为(2﹣3,﹣3+1),即(﹣1,﹣2),
故答案为:(﹣1,﹣2).
15.-5
【分析】利用轴对称的性质求出点Q的坐标即可.
【解答】解:∵点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,
∴a=﹣2,b=﹣3,
∴a+b=﹣2﹣3=﹣5,
故答案为﹣5.
16.【分析】根据点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,可得答案.
【解答】解:∵2+2=2×2,3+=3×,4+=4×,
故答案为:(2,2),(3,),(4,).
17.-1
【分析】根据关于y轴对称的两个的坐标之间的关系,两个点的横坐标互为相反数,纵坐标不变可得a、b的值,再计算即可.
【解答】解:根据关于y轴对称的两个的坐标之间的关系得,
a=﹣2020,b=2019.
∴a+b=﹣2020+2019=﹣1,
故答案为:﹣1.
18.【分析】根据线段的中点坐标公式即可得到结论.
【解答】解:∵点E(a﹣1,a),F(b,a﹣b),
∴中点G(,),
∵中点G恰好位于x轴上,且到y轴的距离是2,
∴,
解得:,,
∴2a+b=或﹣4;
故答案为:或﹣4.
三、解答题
19.解:(1)∵点A,B关于x轴对称,
∴,
解得.
(2)∵点A,B关于y轴对称,
∴,
解得,
∴(4a+b)2019=[4×(﹣1)+3]2019=﹣1.
20.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN∥y轴,
∴m﹣1=﹣3,
解得 m=﹣2.
∴M(﹣3,﹣1),
∴MN=2﹣(﹣1)=3.
21.解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
22.解:(1)A点的坐标是(﹣1,4),B点的坐标是(﹣4,﹣1),C点的坐标是(1,1),
故答案为:(﹣1,4),(﹣4,﹣1),(1,1);
(2)
过C作x轴的垂线,分别过A作EF⊥y轴,过C作FG⊥x轴,过B作BE⊥x轴,BG⊥y轴,EF交BE于E,EF交FG于F,BG交FG于G,
∵A点的坐标是(﹣1,4),B点的坐标是(﹣4,﹣1),C点的坐标是(1,1),
∴EF=4+1=5,BE=1+4=5,AE=4﹣1=3,AF=1﹣(﹣1)=2,CF=4﹣1=3,CG=1+1=2,
∴△ABC的面积S=S正方形EFGB﹣S△BEA﹣S△AFC﹣S△BGC=5×5﹣﹣﹣=9.5.
23.解:(1)若点A在第一象限或第三象限,则a﹣5=1﹣2a,
解得:a=2,
则a﹣5=1﹣2a=﹣3,
∴点A的坐标为(﹣3,﹣3),
若点A在第二象限或第四象限,则a﹣5+1﹣2a=0,
解得a=﹣4,
则a﹣5=﹣9,1﹣2a=9,
∴点A的坐标为(﹣9,9),
综上所述,点A的坐标为(﹣3,﹣3)或(﹣9,9);
(2)∵若点A向右平移若干个单位,其纵坐标不变为(1﹣2a),
又∵点A向右平移若干个单位后与点B(﹣2,﹣3)关于x轴对称,
∴1﹣2a+(﹣3)=0,
a=﹣1a﹣5=﹣1﹣5=﹣6,
1﹣2a=1﹣2×(﹣1)=3,
即点A的坐标为(﹣6,3).
24.解:(1)由题意可得,
(2)由(1)中的平面直角坐标系可得,
校门口的坐标是(1,0),信息楼的坐标是(1,﹣2),综合楼的坐标是(﹣5,﹣3),实验楼的坐标是(﹣4,0);
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置,如下图所示,
25.解:(1)3×(﹣1)+5=2;﹣1+3×5=14,
∴若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为(2,14).
故答案为:(2,14);
(2)设点P的坐标为(a,b),
由题意可知,
解得:,
∴点P的坐标为(2,﹣1);
(3)∵点P(m﹣1,2m)的“﹣3级关联点”为P′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),①P′位于x轴上,
∴m﹣1+(﹣3)×2m=0,
解得:m=,
∴﹣3(m﹣1)+2m=,
∴P′(,0).
②P′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴P′(0,﹣16).
综上所述,点P′的坐标为(,0)或(0,﹣16).
一、选择题(每小题4分,共24分)
1.如果点A(3,m)在x轴上,那么点B(m+2,m﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P的横坐标是﹣3,且到x轴的距离为5,则P点的坐标是( )
A.(5,﹣3)或(﹣5,﹣3) B.(﹣3,5)或(﹣3,﹣5)
C.(﹣3,5) D.(﹣3,﹣5)
3.若点P(x,y)在第二象限,且|x|=2,|y|=3,则x+y=( )
A.﹣1 B.1 C.5 D.﹣5
4.如图,在平面直角坐标系中,线段AB的两个端点是A(1,3),B(2,1).将线段AB沿某一方向平移后,若点A的对应点A′的坐标为(﹣2,0),则点B的对应点B′的坐标为( )
(﹣3,2) B.(﹣1,﹣3) C.(﹣1,﹣2) D.(0,﹣2)
5.如图,在平面直角坐标系中,四边形OABC是矩形,点O是坐标原点,点A,C的坐标分别是(6,0),(0,3),点B在第一象限,则点B的坐标是( )
(3,6) B.(6,3) C.(6,6) D.(3,3)
6.如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为( )
A.(4039,﹣1) B.(4039,1) C.(2020,﹣1) D.(2020,1)
二、填空题(每小题4分,共48分)
7.已知点P(3a+6,2﹣a)在坐标轴上,则点P的坐标为 .
8.若点A(m+2,﹣3)与点B(﹣4,n+5)在二四象限角平分线上,则m+n= .
9.若电影院中5排3号座位记为(5,3),则4排6号座位记为 .
10.点P(x,y)在第二象限,且|x|=5,|y|=7,则点P的坐标是 .
11.将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为 .
12.已知线段AB的长度为3,且AB平行于y轴,A点坐标为(3,2),则B点坐标为 .
13.在平面直角坐标系中,已知P(0,2),Q(﹣3,0).将线段PQ绕点P逆时针旋转90°得到线段PM,点Q的对应点为M,则点M的坐标为 .
14.在平面直角坐标系中,将点P(2,﹣3)先向上平移1个单位长度,再向左平移3个单位长度后,得到点P′,则点P′的坐标为 .
15.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= .
16.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,请你写出三个和谐点的坐标 .
17.已知点A(a,2019)与点B(2020,b)关于y轴对称,则a+b的值为 .
18.教材上曾让同学们探索过线段的中点坐标:在平面直角坐标系中,若两点A(x1,y1)、B(x2,y2),所连线段AB的中点是M,则M的坐标为(,),例如:点A(1,2)、点B(3,6),则线段AB的中点M的坐标为(,),即M(2,4)请利用以上结论解决问题:在平面直角坐标系中,若点E(a﹣1,a),F(b,a﹣b),线段EF的中点G恰好位于x轴上,且到y轴的距离是2,则2a+b的值等于 .
三、解答题(共78分)
19.(8分)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2019的值.
20.(10分)在平面直角坐标系中,已知点M(m﹣1,2m+3).
(1)若点M在y轴上,求m的值.
(2)若点N(﹣3,2),且直线MN∥y轴,求线段MN的长.
21.(12分)已知点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,点C(a+2,b)与点D关于原点对称.
(1)求点A、B、C、D的坐标;
(2)顺次联结点A、D、B、C,求所得图形的面积.
22.(12分)如图,已知△ABC(网格中每个小正方形的边长均为1).
(1)三个顶点坐标分别为:A ,B ,C ;
(2)求三角形ABC的面积.
23.(12分)已知点A(a﹣5,1﹣2a),解答下列问题:
(1)若点A到x轴和y轴的距离相等,求点A的坐标;
(2)若点A向右平移若干个单位后,与点B(﹣2,﹣3)关于x轴对称,求点A的坐标.
24.(12分)如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
25.(12分)在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),则称点Q是点P的“a级关联点”(其中a为常数,且a≠0),例如,点P(1,4)的“2级关联点”为Q(2×1+4,1+2×4),即Q(6,9).
(1)若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为 ;
(2)若点P的“5级关联点”的坐标为(9,﹣3),求点P的坐标;
(3)若点P(m﹣1,2m)的“﹣3级关联点”P′位于坐标轴上.求点P′的坐标.
答案
一、选择题
1.D
【分析】根据x轴上的点的纵坐标为0列式求出m的值,然后计算即可得解.
【解答】解:∵A(3,m)在x轴上,
∴m=0,
∴m+2=2,m﹣3=﹣3,
∴B(m+2,m﹣3)所在的象限是第四象限.
故选:D.
2.B
【分析】点P到x轴的距离为5即P点的纵坐标是5或﹣5,又因为点P的横坐标是﹣3,即可得P点坐标.
【解答】解:∵点P到x轴的距离为5,
∴P点的纵坐标是5或﹣5,
∵点P的横坐标是﹣3,
∴P点的坐标是(﹣3,5)或(﹣3,﹣5).
故选:B.
3.B
【分析】根据第二象限内点的横坐标小于零,纵坐标大于零,可得x、y的值,根据有理数的加法,可得答案.
【解答】解:由P(x、y)在第二象限且|x|=2,|y|=3,得
x=﹣2,y=3.
x+y=﹣2+3=1,
故选:B.
4.C
【分析】利用平移变换的性质解决问题即可.
【解答】解:观察图象可知,点B的对应点B′的坐标为(﹣1,﹣2).
故选:C.
5.B
【分析】根据矩形的性质得出点B的坐标即可.
【解答】解:∵四边形OABC是矩形,
∴OC=AB,CB=OA,
∵点A,C的坐标分别是(6,0),(0,3),
∴AB=3,OA=6,
∴点B坐标为(6,3),
故选:B.
6.A
【分析】根据等腰直角三角形的性质可找出点P1的坐标,结合旋转的性质即可找出点P2、P3、P4、P5、…、的坐标,根据坐标的变化即可找出变化规律“P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数)”,依此规律即可得出结论.
【解答】解:∵A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,
∴P1(1,1).
∵把△AP1B绕点B顺时针旋转180°,得到△BP2C1,
∴P2(3,﹣1).
同理可得出:P3(5,1),P4(7,﹣1),P5(9,1),…,
∴P2n+1(4n+1,1),P2n+2(4n+3,﹣1)(n为自然数).
∵2020=2×1009+2,4×1009+3=4039,
∴P2020(4039,﹣1).
故选:A.
二、填空题
7.(12,0)或(0,4)
【分析】分点P在x轴上,纵坐标为0;在y轴上,横坐标为0,分别列式求出a的值,再求解即可.
【解答】解:当P在x轴上时,2﹣a=0,
解得:a=2,
则3a+6=12,
故P(12,0);
当P在y轴上时,3a+6=0,
解得:a=﹣2,
故2﹣a=4,
则P(0,4).
所以P(12,0)或(0,4).
故答案为:(12,0)或(0,4).
8.0
【分析】由点A(m+2,﹣3)与点B(﹣4,n+5)在二四象限的角平分线上可得m+2与﹣3互为相反数,﹣4与n+5互为相反,从而可求得m,n的值,从而求得m+n的值.
【解答】解:∵A(m+2,﹣3)在二四象限角平分线上,
∴m+2=3,
解得m=1,
∵点B(﹣4,n+5)在二四象限角平分线上,
∴n+5=4,
解得n=﹣1,
∴m+n=1﹣1=0.
故答案为:0.
9.(4,6)
【分析】明确对应关系,排在前,号在后,然后解答.
【解答】解:电影院中的5排3号记为(5,3),
则4排6号记为(4,6).
故答案为:(4,6).
10.(-5,7)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数结合绝对值的性质求出x、y的值,然后写出即可.
【解答】解:∵点P(x,y)在第二象限,且|x|=5,|y|=7,
∴x=﹣5,y=7,
∴点P的坐标为(﹣5,7).
故答案为:(﹣5,7).
11.(-3,3)
【分析】根据向上平移,横坐标不变,纵坐标加可得结论.
【解答】解:将点P(﹣3,1)向上平移2个单位长度得到点Q,则点Q的坐标为(﹣3,1+2),即(﹣3,3),
故答案为:(﹣3,3).
12.(3,-1)或(3,5)
【分析】由AB∥y轴可得A,B两点的横坐标相同,结合AB=3,A(3,2),分B点在A点之上和之下两种情况可求解B点的纵坐标,进而可求解.
【解答】解:∵AB∥y轴,
∴A,B两点的横坐标相同,
∵A(3,2),
∴B点横坐标为3,
∵AB=3,
∴当B点在A点之上时,B点纵坐标为2+3=5,
∴B(3,5);
∴当B点在A点之下时,B点纵坐标为2﹣3=﹣1,
∴B(3,﹣1).
综上B点坐标为(3,﹣1)或(3,5).
故答案为(3,﹣1)或(3,5).
13.(2,-1)
【分析】利用旋转变换的性质作出图形即可解决问题.
【解答】解:如图,由作图可知,M(2,﹣1).
故答案为(2,﹣1).
14.(-1,-2)
【分析】根据平移规律:横坐标右移加,左移减;纵坐标上移加,下移减即可得.
【解答】解:平移后点Q的坐标为(2﹣3,﹣3+1),即(﹣1,﹣2),
故答案为:(﹣1,﹣2).
15.-5
【分析】利用轴对称的性质求出点Q的坐标即可.
【解答】解:∵点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,
∴a=﹣2,b=﹣3,
∴a+b=﹣2﹣3=﹣5,
故答案为﹣5.
16.【分析】根据点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,可得答案.
【解答】解:∵2+2=2×2,3+=3×,4+=4×,
故答案为:(2,2),(3,),(4,).
17.-1
【分析】根据关于y轴对称的两个的坐标之间的关系,两个点的横坐标互为相反数,纵坐标不变可得a、b的值,再计算即可.
【解答】解:根据关于y轴对称的两个的坐标之间的关系得,
a=﹣2020,b=2019.
∴a+b=﹣2020+2019=﹣1,
故答案为:﹣1.
18.【分析】根据线段的中点坐标公式即可得到结论.
【解答】解:∵点E(a﹣1,a),F(b,a﹣b),
∴中点G(,),
∵中点G恰好位于x轴上,且到y轴的距离是2,
∴,
解得:,,
∴2a+b=或﹣4;
故答案为:或﹣4.
三、解答题
19.解:(1)∵点A,B关于x轴对称,
∴,
解得.
(2)∵点A,B关于y轴对称,
∴,
解得,
∴(4a+b)2019=[4×(﹣1)+3]2019=﹣1.
20.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)∵点N(﹣3,2),且直线MN∥y轴,
∴m﹣1=﹣3,
解得 m=﹣2.
∴M(﹣3,﹣1),
∴MN=2﹣(﹣1)=3.
21.解:(1)∵点A(﹣1,3a﹣1)与点B(2b+1,﹣2)关于x轴对称,
∴2b+1=﹣1,3a﹣1=2,
解得a=1,b=﹣1,
∴点A(﹣1,2),B(﹣1,﹣2),C(3,﹣1),
∵点C(a+2,b)与点D关于原点对称,
∴点D(﹣3,1);
(2)如图所示:
四边形ADBC的面积为:.
22.解:(1)A点的坐标是(﹣1,4),B点的坐标是(﹣4,﹣1),C点的坐标是(1,1),
故答案为:(﹣1,4),(﹣4,﹣1),(1,1);
(2)
过C作x轴的垂线,分别过A作EF⊥y轴,过C作FG⊥x轴,过B作BE⊥x轴,BG⊥y轴,EF交BE于E,EF交FG于F,BG交FG于G,
∵A点的坐标是(﹣1,4),B点的坐标是(﹣4,﹣1),C点的坐标是(1,1),
∴EF=4+1=5,BE=1+4=5,AE=4﹣1=3,AF=1﹣(﹣1)=2,CF=4﹣1=3,CG=1+1=2,
∴△ABC的面积S=S正方形EFGB﹣S△BEA﹣S△AFC﹣S△BGC=5×5﹣﹣﹣=9.5.
23.解:(1)若点A在第一象限或第三象限,则a﹣5=1﹣2a,
解得:a=2,
则a﹣5=1﹣2a=﹣3,
∴点A的坐标为(﹣3,﹣3),
若点A在第二象限或第四象限,则a﹣5+1﹣2a=0,
解得a=﹣4,
则a﹣5=﹣9,1﹣2a=9,
∴点A的坐标为(﹣9,9),
综上所述,点A的坐标为(﹣3,﹣3)或(﹣9,9);
(2)∵若点A向右平移若干个单位,其纵坐标不变为(1﹣2a),
又∵点A向右平移若干个单位后与点B(﹣2,﹣3)关于x轴对称,
∴1﹣2a+(﹣3)=0,
a=﹣1a﹣5=﹣1﹣5=﹣6,
1﹣2a=1﹣2×(﹣1)=3,
即点A的坐标为(﹣6,3).
24.解:(1)由题意可得,
(2)由(1)中的平面直角坐标系可得,
校门口的坐标是(1,0),信息楼的坐标是(1,﹣2),综合楼的坐标是(﹣5,﹣3),实验楼的坐标是(﹣4,0);
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置,如下图所示,
25.解:(1)3×(﹣1)+5=2;﹣1+3×5=14,
∴若点P的坐标为(﹣1,5),则它的“3级关联点”的坐标为(2,14).
故答案为:(2,14);
(2)设点P的坐标为(a,b),
由题意可知,
解得:,
∴点P的坐标为(2,﹣1);
(3)∵点P(m﹣1,2m)的“﹣3级关联点”为P′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),①P′位于x轴上,
∴m﹣1+(﹣3)×2m=0,
解得:m=,
∴﹣3(m﹣1)+2m=,
∴P′(,0).
②P′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴P′(0,﹣16).
综上所述,点P′的坐标为(,0)或(0,﹣16).
