数学: 1.1.1 《正弦定理》教案(新人教必修5)
文档属性
| 名称 | 数学: 1.1.1 《正弦定理》教案(新人教必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-13 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.1 正弦定理和余弦定理
课标导读:
1.在已有知识的基础上,通过对任意三角形边角关系的探究,发现并掌握三角形中的边长与角度之间的数量关系—正弦定理。
2.掌握正弦定理,能初步运用正弦定理解一些斜三角形;
3.能够运用正弦定理解决某些与测量和几何有关的实际问题。
情境导入:
2008年青岛奥帆赛成功举办,在比赛中千百艘帆船如离弦之“箭”射向终点,我们知道帆船航行的动力来源于风力,风对帆船的动力与帆船上成三角形的帆布有直接关系, 那我们怎样借助于数学知识设计出比较好的帆船呢?
新知导学:
1.正弦定理 在一个三角形中,各边和它所对角的_______的比相等,即_______。
2.一般地,把三角形的三个角和它们所对的边叫做三角形的 ,已知三角形的几个元素求其它元素的过程叫做 。
3.用正弦定理可解决下列那种问题
1 已知三角形三边;②已知三角形两边与其中一边的对角;③已知三角形两边与第三边的对角;④已知三角形三个内角;⑤已知三角形两角与任一边;⑥已知三角形一个内角与它所对边之外的两边。
诱思探究:
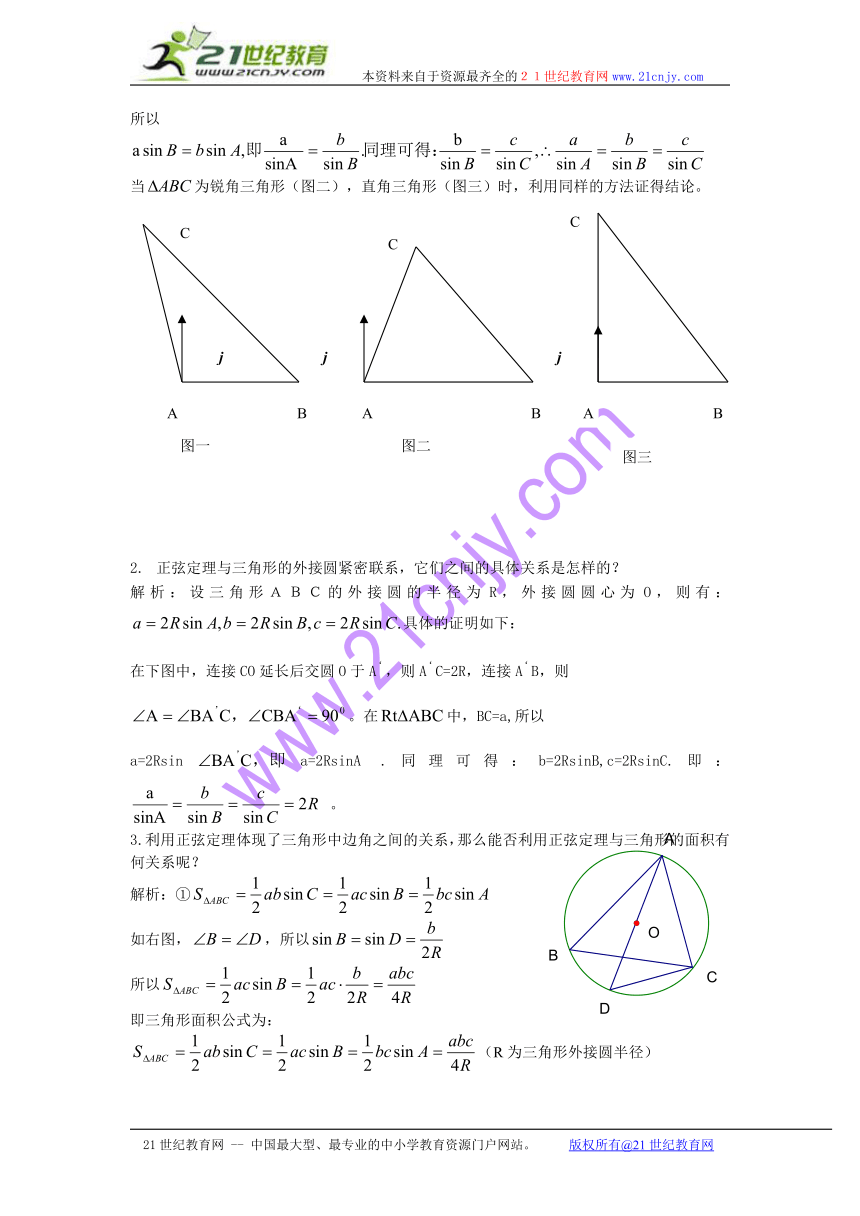
1. 正弦定理除了课本上用几何的方法证明外,和可以用向量的方法进行证明,下面我们以钝角三角形为例进行说明.
解析:在钝角三级形ABC中,如图一中,过A做单位向量j 垂直于,则向量j与为向量j与的夹角为,向量j与的夹角为设AB=c,BC=a,AC=b.因为++=0,所以j(++)=j+ j+ j0。
即 + +0.
所以
当为锐角三角形(图二),直角三角形(图三)时,利用同样的方法证得结论。
2. 正弦定理与三角形的外接圆紧密联系,它们之间的具体关系是怎样的?
解析:设三角形ABC的外接圆的半径为R,外接圆圆心为O,则有:具体的证明如下:
在下图中,连接CO延长后交圆O于A,则AC=2R,连接AB,则
。在中,BC=a,所以
a=2Rsina=2RsinA .同理可得:b=2RsinB,c=2RsinC.即: 。
3.利用正弦定理体现了三角形中边角之间的关系,那么能否利用正弦定理与三角形的面积有何关系呢?
解析:①
如右图,,所以
所以
即三角形面积公式为:
(R为三角形外接圆半径)
疑难导析:
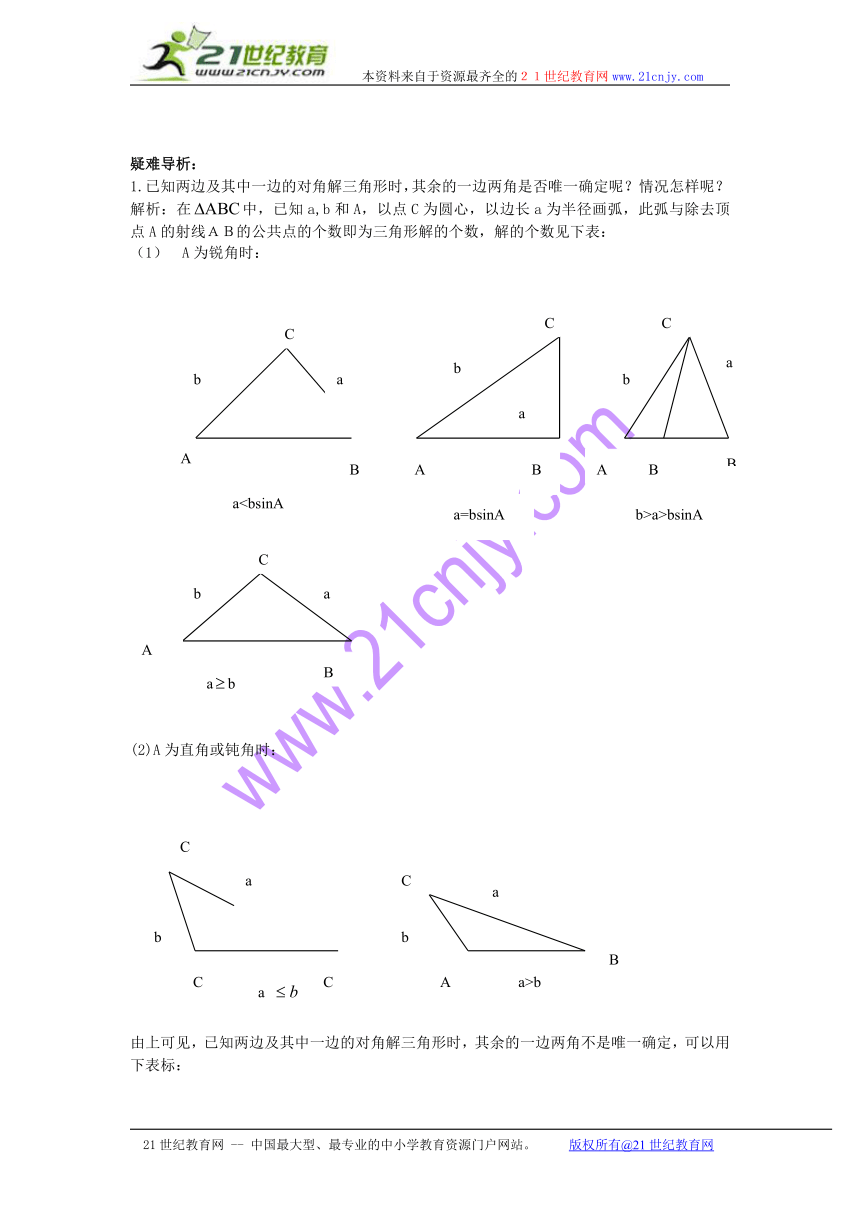
1.已知两边及其中一边的对角解三角形时,其余的一边两角是否唯一确定呢?情况怎样呢?
解析:在中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
(1) A为锐角时:
(2)A为直角或钝角时:
由上可见,已知两边及其中一边的对角解三角形时,其余的一边两角不是唯一确定,可以用下表标:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absinA 两解
a=bsinA 一解
A1. 在问题1.中我们已经知道已知两边及其中一边的对角解三角形时,其余的一边两角不是唯一确定,那如果已知三角形的任意两角与一边,求其它两边和一角的情况怎样呢?这种情况下会有几解呢?
解析:在三角形ABC中,如果已知A,B和b,那C是唯一确定的,利用正弦定理可以发现a,c只有一解,因此如果已知三角形的任意两角与一边,求其它两边和一角只有一种情况,只有一解。
典例导思:
考查目标一:已知三角形两角及其中一角的对边求解三角形。
典例1.已知:在中,,,,解此三角形。
导拨:在该题中,已知C及c,可以利用正弦定理列出方程进行求解。
解析:由,可得
由,可依次计算出,。
规律总结:已知三角形两角及其中一角的对边求解三角形这种情况只有一种,处理方法主要借助于正弦定理解方程,在求方程的过程中我们要分清角及其角的对边,搞清楚各个量之间的关系。
考查目标二:已知三角形两边及其中一边的对角求解三角形。
典例2.已知下列三角形的两边及其一边的对角,判断三角形的情况,有解的作出解答。
(1)a=7,b=9,A=100 (2)a=10,b=20,A=75
(3)a=10,c=5,C=60 (4)a=2
导拨:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体有几解可以借助于《疑难导析》1中的方法解决。
解析:(1)本题无解。
(2)本题无解。
(3)本题有一个解。
利用正弦定理,可得:
(4)本题有两解。
由正弦定理得:
当
综上所述:
规律总结:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体方法可以借助于下了表格:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absinA 两解
a=bsinA 一解
A在线拓展:已知:在中,,,,解此三角形。
解析:由
∴当时, ∴
∴当时, ∴。
考察目标三:求三角形面积。
典例3:在的面积。
导拨:已知三角形两边及其一边的对角,由正弦定理来解题。
解析:根据正弦定理有
则C有两解。
(1)当C为锐角时,
(2)当C为钝角时,
所以,的面积为
规律总结:(R为三角形外接圆半径)
公式中需要知道两边及其夹角,在此题目中需要求出A,而对于A有两种情况,因此该三角形的面积有两解。
考查目标四:正弦定理的综合应用。
典例4:如右图,D是直角斜边BC上的一点,AB=AD,记
(1) 证明:sin(2)若AC=,求的值。
导拨:结合已知条件,利用诱导公式找出角及角的三角函数间关系。
解析:(1)证明: sin。
(2) 在三角形ADC中,由正弦定理可得:
sin
在(1)中sin,
解得:sin
规律总结:正弦定理揭示了任意三角形边角之间的客观关系,是解三角形的重要工具,它经常与三角函数,平面向量知识在三角形中有密切的联系。
分级导练:
基础巩固:
1.已知△ABC中,a=4,b=4,∠A=30°,则∠B等于( D )
A.30° B.30°或150°
C.60° D.60°或120°
1.答案:D。导析:利用正弦定理直接可以求得,要注意解的个数问题。
2.在△ABC中,若,则与的大小关系为( A)
)
A. B. C. ≥ D. 、的大小关系不能确定
2.答案:A。 导析:利用正弦定理可得:
3.在中,若,则等于 ( )
A. B. C. 或 D. 或
3.答案:B。导析:由可得,由正弦定理可知,故可得,故或。
4.已知等腰的腰为底的2倍,则顶角的正切值是 (D )
(A) (B) (C) (D)
4.答案:D。
5.不解三角形,确定下列判断中正确的是 ( )
A. ,有两解 B. ,有一解
C. ,有两解 D. ,无解
5.答案:B。导析:利用三角形中大角对大边,大边对大角定理判定解的个数可知选B。
6.已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为( ).
A.9 B.18 C.9 D.18
6.答案:C 。
7.在△ABC中,若 sinA=,则A= .
7.答案:60°导析: 2sin2A=3cosA,2(1-cos2A)=3cosA,(2cosA-1)(cosA+2)=0,
cosA=2 (舍), ∴cosA=,A=60°.∴A=60°.
8.在中,,,则( )
A. B. C. D.
8.答案:D导析:由比例性质和正弦定理可知。
9.在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c.若sinA:sinB:sinC=5:7:8,则a:b:c= .
9.答案:5:7:8
10.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东,行驶4h后,船到达C处,看到这个灯塔在北偏东,这时船与灯塔的距离为 ______km.
10.答案: 。
11.在中,已知,解此三角形。
11.解析:由正弦定理,即,解得,
因为,所以或,
当时,,为直角三角形,此时;
当时,,,所以。
12.在中,,,,求tanA的值和ΔABC的面积.
12.解析:先解三角方程,求出角A的值.
又,
能力提升:
13.在中,已知,则等于 ( )
A. B. C. D.
13.答案:B。导析:由正弦定理可得,带入可得,由于,所以,,又由正弦定理带入可得。
14.在中,已知,,则的形状是( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
14.解析:由可得,所以,即或,
又由及可知,所以为等腰三角形。
15. 若的内角满足,则 ( D )
A. B C D
15.答案:D
16. △ABC中,若b=2a,B=A+60°,则A= .
16.答案: 30°。导析:由b=2a得sinB=2sinA,又B=A+60°,∴sin(A+60°)=2sinA
∴sinAcos60°+cosAsin60°=2sinA,∴sinA=cosA,∴,
又0°<A<180°,∴A=30°.
17. 在ABC中,设,求A的值。
17. 解析:根据正弦定理:
18.的三个内角为,求当A为何值时,取得最大值,并求出这个最大值.
18.解析: 由A+B+C=π, 得 = - , 所以有cos =sin .cosA+2cos =cosA+2sin =1-2sin2 + 2sin =-2(sin - )2+ ,当sin = , 即A=时, cosA+2cos取得最大值为.
探究拓展:
19. 在中,角A,B,C的对边分别是a,b,c若a+c=2b,
求证:2cos
解析:证明:由正弦定理可得:a=2RsinA,b=2RsinB,c=2RsinC
20.在△ABC中, A、B、C成等差数列,b=1,求证:1<a+c≤2.
20.解析:证法一:由正弦定理:得
[sinA+sin(120°-A)]=2sin(A+30°)
∵0°<A<120°,∴30°<A+30°<150° ∴1<2sin(A+30°)≤2.
证法二 ∵B=60°,b=1,∴a2+c2-b2=2accos60° ∴a2+c2-1=ac,∴a2+c2-ac=1,∴(a+c)2+3(a-c)2=4 ∴(a+c)2=4-3(a-c)2,∵0≤a-c<1 ∴0≤3(a-c)2<3,∴4-3(a-c)2≤4 即(a+c)2≤4,∴a+c≤2, 又a+c>1 ∴1<a+c≤2.
A
B
C
图一
C
B
A
C
B
A
图二
图三
j
j
j
a
C
b
B
C
A
b
B
A
a
C
A
B EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3
b
a
B
C
b
B
A
a
ab>a>bsinA
ab
a=bsinA
C
a
b
C
C
B
A
C
a
a EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3
b
a>b
A
B
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.1 正弦定理和余弦定理
课标导读:
1.在已有知识的基础上,通过对任意三角形边角关系的探究,发现并掌握三角形中的边长与角度之间的数量关系—正弦定理。
2.掌握正弦定理,能初步运用正弦定理解一些斜三角形;
3.能够运用正弦定理解决某些与测量和几何有关的实际问题。
情境导入:
2008年青岛奥帆赛成功举办,在比赛中千百艘帆船如离弦之“箭”射向终点,我们知道帆船航行的动力来源于风力,风对帆船的动力与帆船上成三角形的帆布有直接关系, 那我们怎样借助于数学知识设计出比较好的帆船呢?
新知导学:
1.正弦定理 在一个三角形中,各边和它所对角的_______的比相等,即_______。
2.一般地,把三角形的三个角和它们所对的边叫做三角形的 ,已知三角形的几个元素求其它元素的过程叫做 。
3.用正弦定理可解决下列那种问题
1 已知三角形三边;②已知三角形两边与其中一边的对角;③已知三角形两边与第三边的对角;④已知三角形三个内角;⑤已知三角形两角与任一边;⑥已知三角形一个内角与它所对边之外的两边。
诱思探究:
1. 正弦定理除了课本上用几何的方法证明外,和可以用向量的方法进行证明,下面我们以钝角三角形为例进行说明.
解析:在钝角三级形ABC中,如图一中,过A做单位向量j 垂直于,则向量j与为向量j与的夹角为,向量j与的夹角为设AB=c,BC=a,AC=b.因为++=0,所以j(++)=j+ j+ j0。
即 + +0.
所以
当为锐角三角形(图二),直角三角形(图三)时,利用同样的方法证得结论。
2. 正弦定理与三角形的外接圆紧密联系,它们之间的具体关系是怎样的?
解析:设三角形ABC的外接圆的半径为R,外接圆圆心为O,则有:具体的证明如下:
在下图中,连接CO延长后交圆O于A,则AC=2R,连接AB,则
。在中,BC=a,所以
a=2Rsina=2RsinA .同理可得:b=2RsinB,c=2RsinC.即: 。
3.利用正弦定理体现了三角形中边角之间的关系,那么能否利用正弦定理与三角形的面积有何关系呢?
解析:①
如右图,,所以
所以
即三角形面积公式为:
(R为三角形外接圆半径)
疑难导析:
1.已知两边及其中一边的对角解三角形时,其余的一边两角是否唯一确定呢?情况怎样呢?
解析:在中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
(1) A为锐角时:
(2)A为直角或钝角时:
由上可见,已知两边及其中一边的对角解三角形时,其余的一边两角不是唯一确定,可以用下表标:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absinA 两解
a=bsinA 一解
A
解析:在三角形ABC中,如果已知A,B和b,那C是唯一确定的,利用正弦定理可以发现a,c只有一解,因此如果已知三角形的任意两角与一边,求其它两边和一角只有一种情况,只有一解。
典例导思:
考查目标一:已知三角形两角及其中一角的对边求解三角形。
典例1.已知:在中,,,,解此三角形。
导拨:在该题中,已知C及c,可以利用正弦定理列出方程进行求解。
解析:由,可得
由,可依次计算出,。
规律总结:已知三角形两角及其中一角的对边求解三角形这种情况只有一种,处理方法主要借助于正弦定理解方程,在求方程的过程中我们要分清角及其角的对边,搞清楚各个量之间的关系。
考查目标二:已知三角形两边及其中一边的对角求解三角形。
典例2.已知下列三角形的两边及其一边的对角,判断三角形的情况,有解的作出解答。
(1)a=7,b=9,A=100 (2)a=10,b=20,A=75
(3)a=10,c=5,C=60 (4)a=2
导拨:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体有几解可以借助于《疑难导析》1中的方法解决。
解析:(1)本题无解。
(2)本题无解。
(3)本题有一个解。
利用正弦定理,可得:
(4)本题有两解。
由正弦定理得:
当
综上所述:
规律总结:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体方法可以借助于下了表格:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absinA 两解
a=bsinA 一解
A
解析:由
∴当时, ∴
∴当时, ∴。
考察目标三:求三角形面积。
典例3:在的面积。
导拨:已知三角形两边及其一边的对角,由正弦定理来解题。
解析:根据正弦定理有
则C有两解。
(1)当C为锐角时,
(2)当C为钝角时,
所以,的面积为
规律总结:(R为三角形外接圆半径)
公式中需要知道两边及其夹角,在此题目中需要求出A,而对于A有两种情况,因此该三角形的面积有两解。
考查目标四:正弦定理的综合应用。
典例4:如右图,D是直角斜边BC上的一点,AB=AD,记
(1) 证明:sin(2)若AC=,求的值。
导拨:结合已知条件,利用诱导公式找出角及角的三角函数间关系。
解析:(1)证明: sin。
(2) 在三角形ADC中,由正弦定理可得:
sin
在(1)中sin,
解得:sin
规律总结:正弦定理揭示了任意三角形边角之间的客观关系,是解三角形的重要工具,它经常与三角函数,平面向量知识在三角形中有密切的联系。
分级导练:
基础巩固:
1.已知△ABC中,a=4,b=4,∠A=30°,则∠B等于( D )
A.30° B.30°或150°
C.60° D.60°或120°
1.答案:D。导析:利用正弦定理直接可以求得,要注意解的个数问题。
2.在△ABC中,若,则与的大小关系为( A)
)
A. B. C. ≥ D. 、的大小关系不能确定
2.答案:A。 导析:利用正弦定理可得:
3.在中,若,则等于 ( )
A. B. C. 或 D. 或
3.答案:B。导析:由可得,由正弦定理可知,故可得,故或。
4.已知等腰的腰为底的2倍,则顶角的正切值是 (D )
(A) (B) (C) (D)
4.答案:D。
5.不解三角形,确定下列判断中正确的是 ( )
A. ,有两解 B. ,有一解
C. ,有两解 D. ,无解
5.答案:B。导析:利用三角形中大角对大边,大边对大角定理判定解的个数可知选B。
6.已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积为( ).
A.9 B.18 C.9 D.18
6.答案:C 。
7.在△ABC中,若 sinA=,则A= .
7.答案:60°导析: 2sin2A=3cosA,2(1-cos2A)=3cosA,(2cosA-1)(cosA+2)=0,
cosA=2 (舍), ∴cosA=,A=60°.∴A=60°.
8.在中,,,则( )
A. B. C. D.
8.答案:D导析:由比例性质和正弦定理可知。
9.在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c.若sinA:sinB:sinC=5:7:8,则a:b:c= .
9.答案:5:7:8
10.一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东,行驶4h后,船到达C处,看到这个灯塔在北偏东,这时船与灯塔的距离为 ______km.
10.答案: 。
11.在中,已知,解此三角形。
11.解析:由正弦定理,即,解得,
因为,所以或,
当时,,为直角三角形,此时;
当时,,,所以。
12.在中,,,,求tanA的值和ΔABC的面积.
12.解析:先解三角方程,求出角A的值.
又,
能力提升:
13.在中,已知,则等于 ( )
A. B. C. D.
13.答案:B。导析:由正弦定理可得,带入可得,由于,所以,,又由正弦定理带入可得。
14.在中,已知,,则的形状是( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
14.解析:由可得,所以,即或,
又由及可知,所以为等腰三角形。
15. 若的内角满足,则 ( D )
A. B C D
15.答案:D
16. △ABC中,若b=2a,B=A+60°,则A= .
16.答案: 30°。导析:由b=2a得sinB=2sinA,又B=A+60°,∴sin(A+60°)=2sinA
∴sinAcos60°+cosAsin60°=2sinA,∴sinA=cosA,∴,
又0°<A<180°,∴A=30°.
17. 在ABC中,设,求A的值。
17. 解析:根据正弦定理:
18.的三个内角为,求当A为何值时,取得最大值,并求出这个最大值.
18.解析: 由A+B+C=π, 得 = - , 所以有cos =sin .cosA+2cos =cosA+2sin =1-2sin2 + 2sin =-2(sin - )2+ ,当sin = , 即A=时, cosA+2cos取得最大值为.
探究拓展:
19. 在中,角A,B,C的对边分别是a,b,c若a+c=2b,
求证:2cos
解析:证明:由正弦定理可得:a=2RsinA,b=2RsinB,c=2RsinC
20.在△ABC中, A、B、C成等差数列,b=1,求证:1<a+c≤2.
20.解析:证法一:由正弦定理:得
[sinA+sin(120°-A)]=2sin(A+30°)
∵0°<A<120°,∴30°<A+30°<150° ∴1<2sin(A+30°)≤2.
证法二 ∵B=60°,b=1,∴a2+c2-b2=2accos60° ∴a2+c2-1=ac,∴a2+c2-ac=1,∴(a+c)2+3(a-c)2=4 ∴(a+c)2=4-3(a-c)2,∵0≤a-c<1 ∴0≤3(a-c)2<3,∴4-3(a-c)2≤4 即(a+c)2≤4,∴a+c≤2, 又a+c>1 ∴1<a+c≤2.
A
B
C
图一
C
B
A
C
B
A
图二
图三
j
j
j
a
C
b
B
C
A
b
B
A
a
C
A
B EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3
b
a
B
C
b
B
A
a
a
ab
a=bsinA
C
a
b
C
C
B
A
C
a
a EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3 EMBED Equation.3
b
a>b
A
B
C
D
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
