2015秋鲁教版数学八上5.4《多边形的内角与外角和》ppt课件
文档属性
| 名称 | 2015秋鲁教版数学八上5.4《多边形的内角与外角和》ppt课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 537.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-08 00:00:00 | ||
图片预览




文档简介
课件15张PPT。5.4 多边形的内角和与外角和 矩形拼图 三角形拼图 六边形拼图拼图游戏在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形.
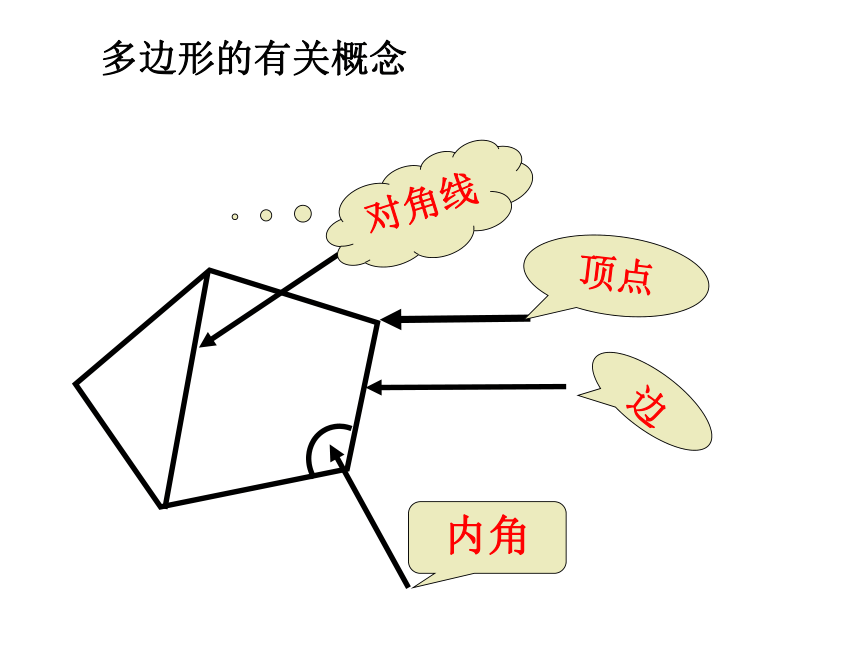
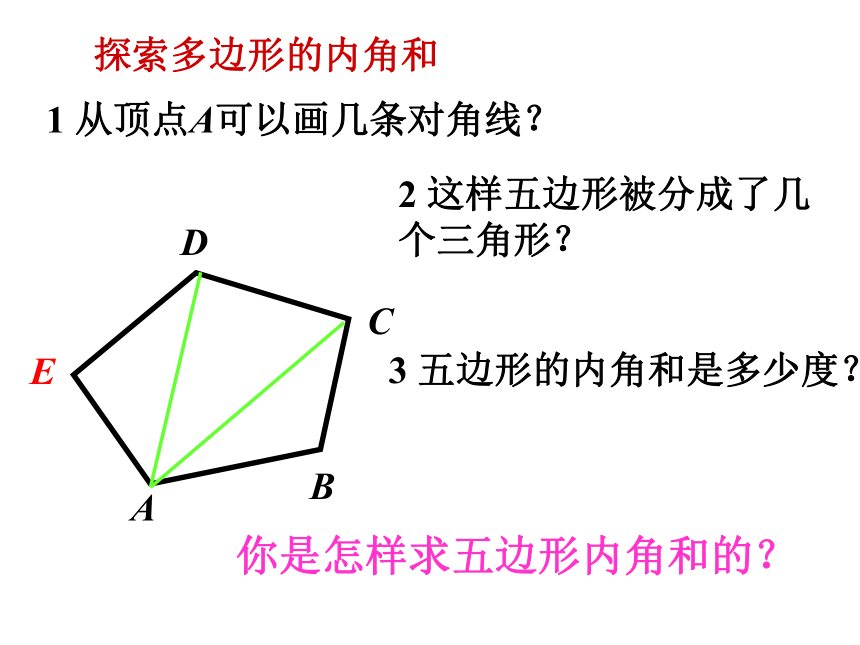
多边形定义顶点边内角对角线多边形的有关概念上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?小明是这样做的.1 从顶点A可以画几条对角线?2 这样五边形被分成了几个三角形?3 五边形的内角和是多少度?
你是怎样求五边形内角和的?探索多边形的内角和 五边形内角和为4×180°-180°=540°五边形内角和为5 ×180°-360° =540°ABCDEOABCDEO连接 OA OB OD 连接 oc OB OE OA OD ABCDE PABCDEAEDBC你来探索六边形的内角和,你一定行!ABDEF44×180°C探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °720 °540 °表中三角形的个数与边数有怎样的关系?多边形的内角和度数与三角形个数有怎样的关系?与边数又有怎样的关系?(n-2) ×180°想一想:观察下面多边形,它们的边,角有什么特点?在平面内,内角都相等,边也都相等的多边形叫做正多边形想一想:正三角形正四边形正五边形正六边形正八边形 上面正多边形的内角各是多少度? 一个多边形的边都相等,它的内角一
定都相等吗?反之结论成立吗?想一想:12边形的内角和是_______已知一个多边形的每个内角为140度则这个多边形 是—————边形 若这多边形边数加1则这多边形的内角和增加———在四边形ABCD中四个内角度数比为2:3:4:3则每个内角—————下列角中能成为一个多边形内角和的是———— A 270度 B 560度 C 1800度 D 1900度练一练: 过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形.这个多边形是---------边形,它的内角和是-------------已知一个多边形的内角和是2340°,则这个多边形的边数是-------------练一练:多边形的有关概念、正多边形、多边形的内角和公式,并能利用公式进行计算. 在学习多边形的有关概念时,我们通过复习三角形的有关概念来类比得出的,这种通过复习旧知识,比较、得出新知识的方法在以往的数学学习中也曾出现过. 我们在研究、探索多边形的内角和公式时,首先从具体的、得出多边形的内角和公式.在研究问题的过程中,特殊的四边形、五边形入手,来把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题,这种研究和探索问题的方法都是我们在学习数学过程中,经常要用到的,希同学们要领悟这种思想方法.课堂小结
多边形定义顶点边内角对角线多边形的有关概念上图中广场中心的边缘是一个五边形,你能设法求出它的五个内角的和吗?小明是这样做的.1 从顶点A可以画几条对角线?2 这样五边形被分成了几个三角形?3 五边形的内角和是多少度?
你是怎样求五边形内角和的?探索多边形的内角和 五边形内角和为4×180°-180°=540°五边形内角和为5 ×180°-360° =540°ABCDEOABCDEO连接 OA OB OD 连接 oc OB OE OA OD ABCDE PABCDEAEDBC你来探索六边形的内角和,你一定行!ABDEF44×180°C探索多边形的内角和这种探索方法你掌握了吗?请完成下表345n-2900 °720 °540 °表中三角形的个数与边数有怎样的关系?多边形的内角和度数与三角形个数有怎样的关系?与边数又有怎样的关系?(n-2) ×180°想一想:观察下面多边形,它们的边,角有什么特点?在平面内,内角都相等,边也都相等的多边形叫做正多边形想一想:正三角形正四边形正五边形正六边形正八边形 上面正多边形的内角各是多少度? 一个多边形的边都相等,它的内角一
定都相等吗?反之结论成立吗?想一想:12边形的内角和是_______已知一个多边形的每个内角为140度则这个多边形 是—————边形 若这多边形边数加1则这多边形的内角和增加———在四边形ABCD中四个内角度数比为2:3:4:3则每个内角—————下列角中能成为一个多边形内角和的是———— A 270度 B 560度 C 1800度 D 1900度练一练: 过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形.这个多边形是---------边形,它的内角和是-------------已知一个多边形的内角和是2340°,则这个多边形的边数是-------------练一练:多边形的有关概念、正多边形、多边形的内角和公式,并能利用公式进行计算. 在学习多边形的有关概念时,我们通过复习三角形的有关概念来类比得出的,这种通过复习旧知识,比较、得出新知识的方法在以往的数学学习中也曾出现过. 我们在研究、探索多边形的内角和公式时,首先从具体的、得出多边形的内角和公式.在研究问题的过程中,特殊的四边形、五边形入手,来把多边形问题通过分割成三角形来研究,即把复杂问题转化为简单问题,这种研究和探索问题的方法都是我们在学习数学过程中,经常要用到的,希同学们要领悟这种思想方法.课堂小结
