期中备考:因数与倍数典型例题与过关练习-数学五年级下册苏教版(含答案)
文档属性
| 名称 | 期中备考:因数与倍数典型例题与过关练习-数学五年级下册苏教版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 528.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中备考:因数与倍数典型例题与过关练习-数学五年级下册苏教版
典型例题
1.王叔叔参加社区抽奖活动,下面是他抽到的号码。这个号码是个四位数,同时也是2、3、5的倍数。王叔叔抽到的号码可能是多少?(写出所有可能)
祝你好运! 23
2.有三个连续的自然数,它们的和是三位数,且是2和5的倍数,这个三位数最小是多少?此时这三个连续的自然数分别是多少?想一想,三个连续的自然数的和是几的倍数?
3.2021年端午节到来之际,为了弘扬传统文化,实验小学开展了“我们的节日——端午”主题活动。其中五年级参加划旱地龙舟的学生在20人~30人之间,赛前预演时,无论4人一组或6人一组都剩余2人,请问五年级参加划旱地龙舟的学生有多少人?
4.为了布置教室,小华将一张长24厘米、宽16厘米的彩纸裁成同样大小的正方形,如果要求彩纸没有剩余,裁出的正方形边长最大是多少厘米?一共可以裁出多少个这样的正方形?
1.王叔叔抽到的号码可能是2130,2430,2730。
【分析】同时被2、3、5整除的特征:个位是0且每个数位上的数字之和是3的倍数。据此解答。
【详解】因千位、十位、个位上的数字分别是2、3、0、这三个数字之和是5,所以:和5相加是3的倍数的数有:;
;
答:王叔叔抽到的号码可能是2130、2430、2730。
2.这个三位数最小是120,此时这三个连续的自然数分别是39、40、41;三个连续的自然数的和是3的倍数。
【分析】本题考查2、3和5的倍数的特征。设三个连续的自然数分别是a-1、a和a+1,它们的和是(a-1)+a+(a+1)=3a,所以任意三个连续的自然数之和一定是3的倍数。这个三位数同时是2,3和5的倍数,它的个位上是0,且各个数位上的数字之和是3的倍数,所以这个三位数最小是120,120÷3=40,这三个连续的自然数分别是39、40、41。
【详解】设三个连续的自然数分别是a-1、a和a+1,它们的和是(a-1)+a+(a+1)=3a,所以任意三个连续的自然数之和一定是3的倍数。它们的和又同时是2和5的倍数,即个位上的数只能是0,最小的数字组合为:,故同时是2、3和5的倍数的最小三位数是120。
中间的数为:120÷3=40,则前一个数为:40-1=39,后一个数为:40+1=41。
答:这个三位数最小是120,此时这三个连续的自然数分别是39、40、41,三个连续的自然数的和是3的倍数。
3.26人
【分析】根据题意,五年级参加旱地龙舟的学生人数在20人~30人之间,无论4人或6人一组都省2人,求出4和6的公倍数,在20~30之间,求出倍数再加上2,就是参加旱地龙舟的学生人数。
【详解】4的倍数:4、8、12、16、20、24、28、32……
6的倍数:6、12、18、24、30……
4和6在20~30之间的倍数是24
24+2=26(人)
答:五年级参加旱地龙舟的学生有26人。
【点睛】本题考查两个数的公倍数的求法。
4.8厘米;6个
【分析】根据题意可知,裁出的正方形边长最大是多少,是求24和16的最大公因数;由于是把这个长方形的彩纸正好裁完,没有剩余,即可以用这张纸的面积除以正方形面积,由此即可解答。
【详解】24=2×2×2×3
16=2×2×2×2
24和16的最大公因数:
2×2×2
=4×2
=8(厘米)
24×16÷(8×8)
=384÷64
=6(个)
答:裁出的正方形的边长最大是8厘米,一共可以裁出6个这样的正方形。
【点睛】此题主要考查求两个数的最大公因数,能够根据求最大公因数的方法解决有关的实际问题。
过关练习
1.圈出下面表格中所有的质数,并填一填。
(1)2~50这些数中,质数有( )个,其中最大的是( ),最小的是( )。
(2)2~50这些数中,既是质数又是偶数的是( )。
(3)2~50这些数中,既是合数又是奇数的有( )。
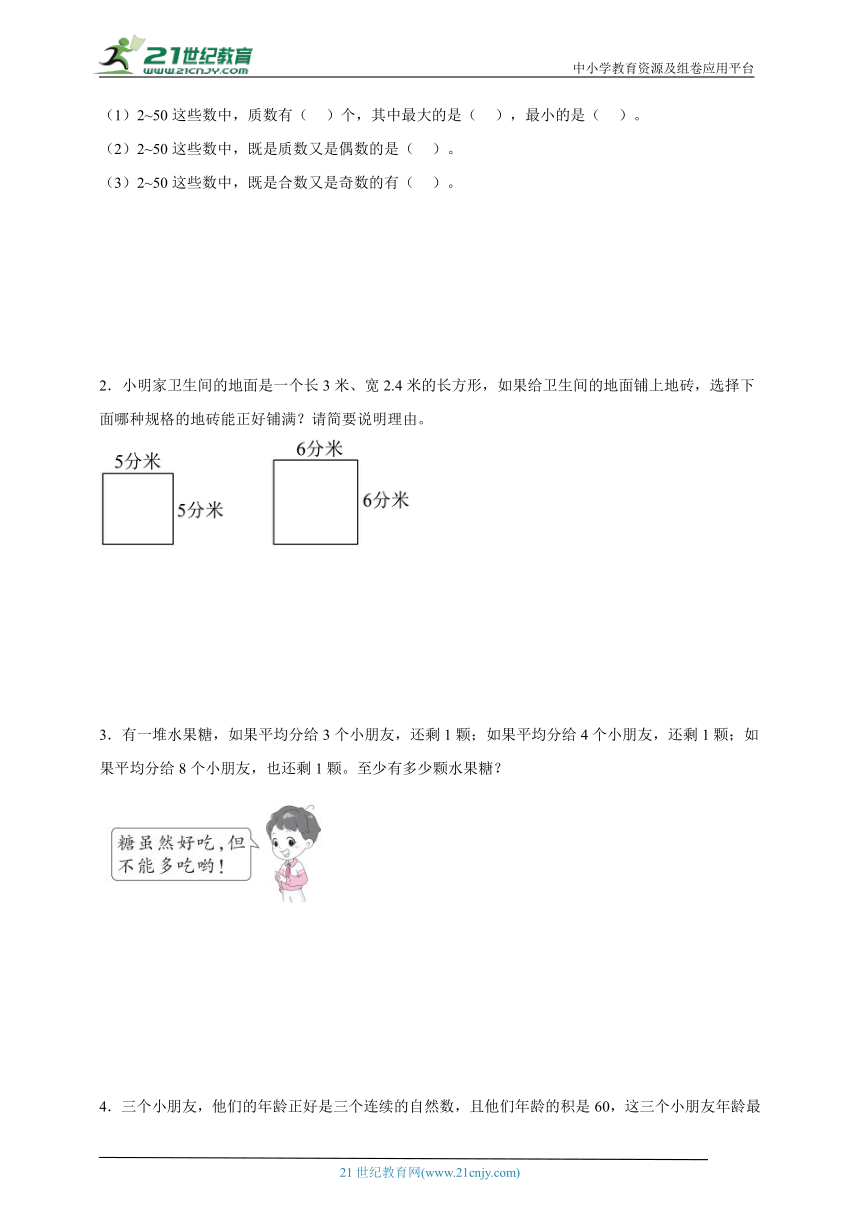
2.小明家卫生间的地面是一个长3米、宽2.4米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
3.有一堆水果糖,如果平均分给3个小朋友,还剩1颗;如果平均分给4个小朋友,还剩1颗;如果平均分给8个小朋友,也还剩1颗。至少有多少颗水果糖?
4.三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是60,这三个小朋友年龄最大的是多少岁?
5.63个小朋友参加表演,如果每5个小朋友分成一组,那么至少再来几个小朋友才能正好分完?如果既能平均分成五组又能平均分成两组,那么至少要去掉几个小朋友?
6.一条跑道长96米,原来从起点到终点每隔3米插一面红旗,现在改成每隔4米插一面红旗,不需要移动的红旗有几面?
7.一篮苹果,5个5个地数,最后还差4个,7个7个地数,最后还余下1个。这篮苹果最少有多少个?
8.亮亮和丽丽去图书馆借书,亮亮每4天去一次,丽丽每7天去一次,7月31日他们两人在图书馆相遇,下一次相遇是几月几日?
9.爸爸今年48岁了,乐乐的年龄是6的倍数,也是爸爸年龄的因数。乐乐今年可能多少岁了?
10.小熊饼干每袋有7块。把下表填写完整,并填空。
袋数 1 2 3 4 5 6 7
饼干块数 7 14
(1)小熊饼干的块数一定是7的( )。
(2)表中7的倍数有( )。
参考答案:
1.
图见详解
(1)15;47;2
(2)2
(3)9、15、21、25、27、33、35、39、45、49
【分析】质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。合数指自然数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。1既不是质数也不是合数。如果一个数能被2整除,则该数是偶数;如果不能被2整除,则该数是奇数。根据质数、合数、奇数、偶数的概念解答。
【详解】2~50的偶数有2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50;
奇数有1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49;
质数如图所示,没画圈的数都是合数;
(1)2~50这些数中,质数有(15)个,其中最大的是(47),最小的是(2)。
(2)2~50这些数中,既是质数又是偶数的是(2)。
(3)2~50这些数中,既是合数又是奇数的有(9、15、21、25、27、33、35、39、45、49)。
2.6分米;理由见详解
【分析】根据题意,要将正方形地砖铺满长方形的区域,找到长和宽的公因数作为正方形的边长,则可正好铺满,据此解答。注意地砖的边长以分米为单位,可先将所有单位换算为分米,1米=10分米。
【详解】3米=30分米
2.4米=24分米
30的因数有:1、2、3、5、6、10、15、30;
24的因数有:1、2、3、4、6、8、12、24;
30和24的公因数有:1、2、3、6;
5不是30和24的公因数,6是30和24的公因数,所以选边长是6分米的正方形地砖能正好铺满;
答:选边长是6分米的正方形地砖能正好铺满,因为6是30和24的公因数。
3.25颗
【分析】根据题意,水果糖平均分给3个、4个、8个小朋友都还剩1颗,则水果糖的颗数比3、4、8的公倍数多1;问至少有多少颗水果糖,则水果糖的颗数为3、4、8的最小公倍数加1,据此解答。
【详解】
3、4、8的最小公倍数是:
(颗)
答:至少有25颗水果糖。
4.5岁
【分析】本题考查利用分解质因数解决问题,可先把60分解质因数,然后把结果写成三个连续自然数的积的形式,即可求得这三个小朋友中最大的年龄。
【详解】60=2×2×3×5
=3×4×5
因为3<4<5
因此年龄最大的是5岁。
答:这三个小朋友年龄最大的是5岁。
【点睛】
5.2个;3个
【分析】5个小朋友分成一组,要求正好分完,则小朋友的个数是5的倍数,即个位上是0或者5,比63大的个位上是5的数最小是65,所以至少再来65-63=2(个)小朋友。既能平均分成五组又能平均分成两组,则小朋友的个数是2和5的倍数,即个位上是0,比63小的个位上是0的数最大是60,所以至少要去掉63-60=3(个)小朋友。据此解答。
【详解】(个)
(组)
(个)
(个)
(个)
答:如果每5个小朋友分成一组,那么至少再来2个小朋友才能正好分完;如果既能平均分成五组又能平均分成两组,那么至少要去掉2个小朋友。
6.9面
【分析】3和4的最小公倍数是12,所以每12米有1面红旗不需要移动,96÷12+1=9(面),注意不能遗漏第1面!
【详解】3和4的最小公倍数是12
96÷12+1
=8+1
=9(面)
答:不需要移动的红旗有9面。
7.36个
【分析】本题考查最小公倍数的应用。5个5个地数差4个,也就是5个5个地数会余下1个;又因为7个7个地数,苹果也余下1个,所以如果拿走1个苹果,那么苹果的个数是5和7的公倍数,所以这篮苹果最少时,个数比5和7的最小公倍数多1个,5和7的最小公倍数是35,据此解答即可。
【详解】5和7的最小公倍数是35,35+1=36(个)
答:这篮苹果最少有36个。
8.8月28日
【分析】4和7 的最小公倍数是28,也就是每28天两人同时去图书馆借书一次,7月31日再过28天是8月 28日,所以下一次相遇是8月28日。
【详解】4和7的最小公倍数是28,所以他们下一次相遇是8月28日。
答:下一次相遇是8月28日。
【点睛】本题考查了最小公倍数的应用 。
9.可能是6岁或12岁或24岁。
【分析】由题意知:在48的范围内找出6的倍数,并根据生活实际进行判断,从而找出合理的数值即可。
【详解】48的因数有:1、2、3、4、6、8、12、16、24、48。
6的倍数有:6、12、18、24、30、36、42、48…
既是6的倍数,又是48的因数的有:6、12、24、48。
乐乐要比爸爸小,所以乐乐今年可能是6岁或12岁或24岁。
答:乐乐今年可能是6岁或12岁或24岁。
10.
21;28;35;42;49
(1)倍数
(2)7、14、21、28、35、42、49
【分析】每袋饼干的数量×袋数=饼干块数,在乘法算式a×b=c(a、b、c均为非0的自然数)中,c是a、b的倍数,所以饼干块数是每袋饼干数量的倍数,即小熊饼干的块数是7的倍数,然后依次写出表中7的倍数即可。
【详解】
填表如下:
袋数 1 2 3 4 5 6 7
饼干块数 7 14 21 28 35 42 49
由分析可知:
(1)小熊饼干的块数一定是7的倍数。
(2)表中7的倍数有7、14、21、28、35、42、49。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中备考:因数与倍数典型例题与过关练习-数学五年级下册苏教版
典型例题
1.王叔叔参加社区抽奖活动,下面是他抽到的号码。这个号码是个四位数,同时也是2、3、5的倍数。王叔叔抽到的号码可能是多少?(写出所有可能)
祝你好运! 23
2.有三个连续的自然数,它们的和是三位数,且是2和5的倍数,这个三位数最小是多少?此时这三个连续的自然数分别是多少?想一想,三个连续的自然数的和是几的倍数?
3.2021年端午节到来之际,为了弘扬传统文化,实验小学开展了“我们的节日——端午”主题活动。其中五年级参加划旱地龙舟的学生在20人~30人之间,赛前预演时,无论4人一组或6人一组都剩余2人,请问五年级参加划旱地龙舟的学生有多少人?
4.为了布置教室,小华将一张长24厘米、宽16厘米的彩纸裁成同样大小的正方形,如果要求彩纸没有剩余,裁出的正方形边长最大是多少厘米?一共可以裁出多少个这样的正方形?
1.王叔叔抽到的号码可能是2130,2430,2730。
【分析】同时被2、3、5整除的特征:个位是0且每个数位上的数字之和是3的倍数。据此解答。
【详解】因千位、十位、个位上的数字分别是2、3、0、这三个数字之和是5,所以:和5相加是3的倍数的数有:;
;
答:王叔叔抽到的号码可能是2130、2430、2730。
2.这个三位数最小是120,此时这三个连续的自然数分别是39、40、41;三个连续的自然数的和是3的倍数。
【分析】本题考查2、3和5的倍数的特征。设三个连续的自然数分别是a-1、a和a+1,它们的和是(a-1)+a+(a+1)=3a,所以任意三个连续的自然数之和一定是3的倍数。这个三位数同时是2,3和5的倍数,它的个位上是0,且各个数位上的数字之和是3的倍数,所以这个三位数最小是120,120÷3=40,这三个连续的自然数分别是39、40、41。
【详解】设三个连续的自然数分别是a-1、a和a+1,它们的和是(a-1)+a+(a+1)=3a,所以任意三个连续的自然数之和一定是3的倍数。它们的和又同时是2和5的倍数,即个位上的数只能是0,最小的数字组合为:,故同时是2、3和5的倍数的最小三位数是120。
中间的数为:120÷3=40,则前一个数为:40-1=39,后一个数为:40+1=41。
答:这个三位数最小是120,此时这三个连续的自然数分别是39、40、41,三个连续的自然数的和是3的倍数。
3.26人
【分析】根据题意,五年级参加旱地龙舟的学生人数在20人~30人之间,无论4人或6人一组都省2人,求出4和6的公倍数,在20~30之间,求出倍数再加上2,就是参加旱地龙舟的学生人数。
【详解】4的倍数:4、8、12、16、20、24、28、32……
6的倍数:6、12、18、24、30……
4和6在20~30之间的倍数是24
24+2=26(人)
答:五年级参加旱地龙舟的学生有26人。
【点睛】本题考查两个数的公倍数的求法。
4.8厘米;6个
【分析】根据题意可知,裁出的正方形边长最大是多少,是求24和16的最大公因数;由于是把这个长方形的彩纸正好裁完,没有剩余,即可以用这张纸的面积除以正方形面积,由此即可解答。
【详解】24=2×2×2×3
16=2×2×2×2
24和16的最大公因数:
2×2×2
=4×2
=8(厘米)
24×16÷(8×8)
=384÷64
=6(个)
答:裁出的正方形的边长最大是8厘米,一共可以裁出6个这样的正方形。
【点睛】此题主要考查求两个数的最大公因数,能够根据求最大公因数的方法解决有关的实际问题。
过关练习
1.圈出下面表格中所有的质数,并填一填。
(1)2~50这些数中,质数有( )个,其中最大的是( ),最小的是( )。
(2)2~50这些数中,既是质数又是偶数的是( )。
(3)2~50这些数中,既是合数又是奇数的有( )。
2.小明家卫生间的地面是一个长3米、宽2.4米的长方形,如果给卫生间的地面铺上地砖,选择下面哪种规格的地砖能正好铺满?请简要说明理由。
3.有一堆水果糖,如果平均分给3个小朋友,还剩1颗;如果平均分给4个小朋友,还剩1颗;如果平均分给8个小朋友,也还剩1颗。至少有多少颗水果糖?
4.三个小朋友,他们的年龄正好是三个连续的自然数,且他们年龄的积是60,这三个小朋友年龄最大的是多少岁?
5.63个小朋友参加表演,如果每5个小朋友分成一组,那么至少再来几个小朋友才能正好分完?如果既能平均分成五组又能平均分成两组,那么至少要去掉几个小朋友?
6.一条跑道长96米,原来从起点到终点每隔3米插一面红旗,现在改成每隔4米插一面红旗,不需要移动的红旗有几面?
7.一篮苹果,5个5个地数,最后还差4个,7个7个地数,最后还余下1个。这篮苹果最少有多少个?
8.亮亮和丽丽去图书馆借书,亮亮每4天去一次,丽丽每7天去一次,7月31日他们两人在图书馆相遇,下一次相遇是几月几日?
9.爸爸今年48岁了,乐乐的年龄是6的倍数,也是爸爸年龄的因数。乐乐今年可能多少岁了?
10.小熊饼干每袋有7块。把下表填写完整,并填空。
袋数 1 2 3 4 5 6 7
饼干块数 7 14
(1)小熊饼干的块数一定是7的( )。
(2)表中7的倍数有( )。
参考答案:
1.
图见详解
(1)15;47;2
(2)2
(3)9、15、21、25、27、33、35、39、45、49
【分析】质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。合数指自然数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。1既不是质数也不是合数。如果一个数能被2整除,则该数是偶数;如果不能被2整除,则该数是奇数。根据质数、合数、奇数、偶数的概念解答。
【详解】2~50的偶数有2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50;
奇数有1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49;
质数如图所示,没画圈的数都是合数;
(1)2~50这些数中,质数有(15)个,其中最大的是(47),最小的是(2)。
(2)2~50这些数中,既是质数又是偶数的是(2)。
(3)2~50这些数中,既是合数又是奇数的有(9、15、21、25、27、33、35、39、45、49)。
2.6分米;理由见详解
【分析】根据题意,要将正方形地砖铺满长方形的区域,找到长和宽的公因数作为正方形的边长,则可正好铺满,据此解答。注意地砖的边长以分米为单位,可先将所有单位换算为分米,1米=10分米。
【详解】3米=30分米
2.4米=24分米
30的因数有:1、2、3、5、6、10、15、30;
24的因数有:1、2、3、4、6、8、12、24;
30和24的公因数有:1、2、3、6;
5不是30和24的公因数,6是30和24的公因数,所以选边长是6分米的正方形地砖能正好铺满;
答:选边长是6分米的正方形地砖能正好铺满,因为6是30和24的公因数。
3.25颗
【分析】根据题意,水果糖平均分给3个、4个、8个小朋友都还剩1颗,则水果糖的颗数比3、4、8的公倍数多1;问至少有多少颗水果糖,则水果糖的颗数为3、4、8的最小公倍数加1,据此解答。
【详解】
3、4、8的最小公倍数是:
(颗)
答:至少有25颗水果糖。
4.5岁
【分析】本题考查利用分解质因数解决问题,可先把60分解质因数,然后把结果写成三个连续自然数的积的形式,即可求得这三个小朋友中最大的年龄。
【详解】60=2×2×3×5
=3×4×5
因为3<4<5
因此年龄最大的是5岁。
答:这三个小朋友年龄最大的是5岁。
【点睛】
5.2个;3个
【分析】5个小朋友分成一组,要求正好分完,则小朋友的个数是5的倍数,即个位上是0或者5,比63大的个位上是5的数最小是65,所以至少再来65-63=2(个)小朋友。既能平均分成五组又能平均分成两组,则小朋友的个数是2和5的倍数,即个位上是0,比63小的个位上是0的数最大是60,所以至少要去掉63-60=3(个)小朋友。据此解答。
【详解】(个)
(组)
(个)
(个)
(个)
答:如果每5个小朋友分成一组,那么至少再来2个小朋友才能正好分完;如果既能平均分成五组又能平均分成两组,那么至少要去掉2个小朋友。
6.9面
【分析】3和4的最小公倍数是12,所以每12米有1面红旗不需要移动,96÷12+1=9(面),注意不能遗漏第1面!
【详解】3和4的最小公倍数是12
96÷12+1
=8+1
=9(面)
答:不需要移动的红旗有9面。
7.36个
【分析】本题考查最小公倍数的应用。5个5个地数差4个,也就是5个5个地数会余下1个;又因为7个7个地数,苹果也余下1个,所以如果拿走1个苹果,那么苹果的个数是5和7的公倍数,所以这篮苹果最少时,个数比5和7的最小公倍数多1个,5和7的最小公倍数是35,据此解答即可。
【详解】5和7的最小公倍数是35,35+1=36(个)
答:这篮苹果最少有36个。
8.8月28日
【分析】4和7 的最小公倍数是28,也就是每28天两人同时去图书馆借书一次,7月31日再过28天是8月 28日,所以下一次相遇是8月28日。
【详解】4和7的最小公倍数是28,所以他们下一次相遇是8月28日。
答:下一次相遇是8月28日。
【点睛】本题考查了最小公倍数的应用 。
9.可能是6岁或12岁或24岁。
【分析】由题意知:在48的范围内找出6的倍数,并根据生活实际进行判断,从而找出合理的数值即可。
【详解】48的因数有:1、2、3、4、6、8、12、16、24、48。
6的倍数有:6、12、18、24、30、36、42、48…
既是6的倍数,又是48的因数的有:6、12、24、48。
乐乐要比爸爸小,所以乐乐今年可能是6岁或12岁或24岁。
答:乐乐今年可能是6岁或12岁或24岁。
10.
21;28;35;42;49
(1)倍数
(2)7、14、21、28、35、42、49
【分析】每袋饼干的数量×袋数=饼干块数,在乘法算式a×b=c(a、b、c均为非0的自然数)中,c是a、b的倍数,所以饼干块数是每袋饼干数量的倍数,即小熊饼干的块数是7的倍数,然后依次写出表中7的倍数即可。
【详解】
填表如下:
袋数 1 2 3 4 5 6 7
饼干块数 7 14 21 28 35 42 49
由分析可知:
(1)小熊饼干的块数一定是7的倍数。
(2)表中7的倍数有7、14、21、28、35、42、49。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
