期中备考:圆柱与圆锥典型例题与过关练习-数学六年级下册苏教版(含答案)
文档属性
| 名称 | 期中备考:圆柱与圆锥典型例题与过关练习-数学六年级下册苏教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 672.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中备考:圆柱与圆锥典型例题与过关练习-数学六年级下册苏教版
典型例题
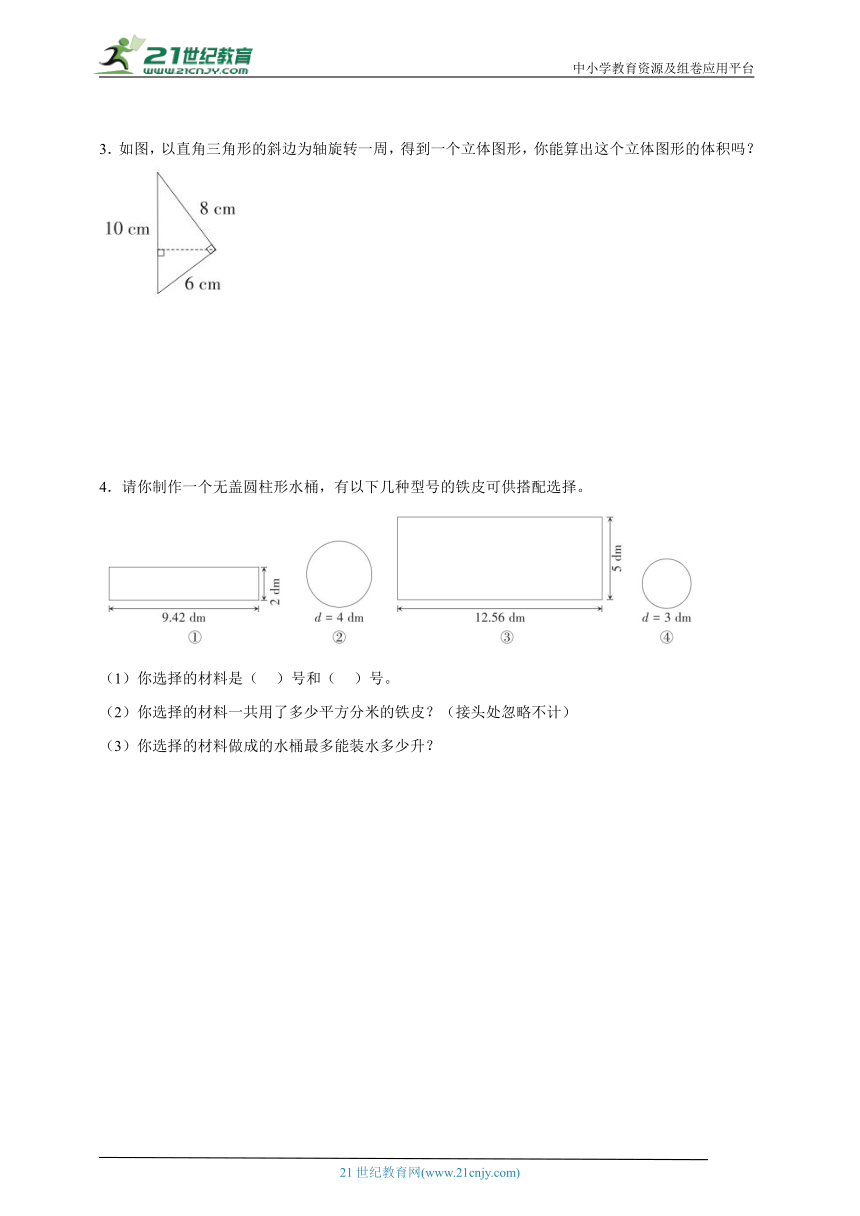
1.用丝带捆扎下面的圆柱形蛋糕盒,打结处正好是底面圆心,打结用去32厘米长的丝带,捆扎这个蛋糕盒至少用去多少厘米丝带?
2.小东利用两种方法分别测量两个石块的体积:
方法1:利用盛水的容器
方法2:利用橡皮泥,比较裹住石块前后揉成的长方体体积。
(1)这两种方法相同的地方是 。
(2)请选择一种你喜欢的方法计算该石块的体积。
3.如图,以直角三角形的斜边为轴旋转一周,得到一个立体图形,你能算出这个立体图形的体积吗?
4.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你选择的材料是( )号和( )号。
(2)你选择的材料一共用了多少平方分米的铁皮?(接头处忽略不计)
(3)你选择的材料做成的水桶最多能装水多少升?
1.172厘米
【分析】
看图,丝带长包括4条底面直径、4条高和打结处的长度,将这三部分的长度相加求出捆扎这个蛋糕盒至少用去多少厘米丝带。
【详解】
20×4+15×4+32
=80+60+32
=172(厘米)
答:捆扎这个蛋糕盒至少用去172厘米丝带。
2.(1)都运用了转化法
(2)一个100.48立方厘米,另一个96立方厘米
【分析】
(1)方法1:将石块的体积转化成圆柱体积进行计算;方法2:将石块的体积转化成长方体体积进行计算。
(2)水面上升的体积就是石块的体积,圆柱底面积×水面上升的高度=石块的体积;橡皮泥前后体积差就是石块的体积,根据长方体体积=长×宽×高,分别求出裹住石块前后的体积,求差即可。
【详解】
(1)这两种方法相同的地方是都运用了转化法。
(2)方法1:3.14×(8÷2)2×(8-6)
=3.14×42×2
=3.14×16×2
=100.48(立方厘米)
方法2:8×4×6-8×2×6
=192-96
=96(立方厘米)
答:一个石块的体积是100.48立方厘米,另一个石块的体积是96立方厘米。
3.241.152立方厘米
【分析】
观察图形可知,以斜边为轴旋转一周,得到的立体图形是上下两个圆锥体,是一个底面半径是(8×6÷2×2÷10)厘米,高的和是10厘米,由此利用圆锥的体积=πr2h,求出两个圆锥的体积再相加,即可解答。
【详解】
底面半径:8×6÷2×2÷10
=48÷2×2÷10
=24×2÷10
=48÷10
=4.8(厘米)
体积:
=×3.14×23.04×10
=×72.3456×10
=24.1152×10
=241.152(立方厘米)
答:这个立体图形的体积241.152立方厘米。
4.(1)①;④
(2)25.905平方分米
(3)14.13升
【分析】
(1)圆柱侧面沿高展开是个长方形,长方形的长或宽等于圆柱底面周长,据此根据圆的周长=圆周率×直径,求出②和④的周长,选择能与之组成圆柱的长方形铁皮即可。
(2)无盖圆柱形水桶只有一个底面,铁皮面积=侧面积+底面积,侧面积=底面周长×高,据此列式解答。
(3)根据圆柱体积=底面积×高,求出水桶容积即可。
【详解】
(1)3.14×4=12.56(分米)
3.14×3=9.42(分米)
选择的材料是①号和④号或②号和③号。
(2)如果选择①号和④号。
9.42×2+3.14×(3÷2)2
=18.84+3.14×1.52
=18.84+3.14×2.25
=18.84+7.065
=25.905(平方分米)
如果选择②号和③号。
12.56×5+3.14×(4÷2)2
=62.8+3.14×22
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:如果选择①号和④号一共用了25.905平方分米的铁皮;如果选择②号和③号一共用了75.36平方分米的铁皮
(3)如果选择①号和④号。
3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=14.13(立方分米)
=14.13(升)
如果选择②号和③号。
3.14×(4÷2)2×5
=3.14×22×5
=3.14×4×5
=62.8(立方分米)
=62.8(升)
答:如果选择①号和④号做成的水桶最多能装水14.13升;如果选择②号和③号做成的水桶最多能装水62.8升。
过关练习
1.一个圆锥形沙堆,底面直径为6米,高是1米,每立方米的沙子重1.5吨。
西樵大桥禁止20吨以上车辆通行,过往车辆请绕道行驶。
(1)林叔叔用一辆空车质量是3吨的卡车一次性运走这堆沙子,能从西樵大桥上通过吗?(写出计算过程)
(2)用这堆沙子在10米宽的公路上铺3厘米厚的路面,能够铺多少米?
2.元代的一种圆形钱币(如图)直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,求垒起来的钱币的体积大约是多少立方厘米?
3.如图,粮囤上面是圆锥形,下面是圆柱形,圆柱的底面周长是12.56米,高是2米,圆锥的高是1.2米。一个粮囤的体积是多少立方米?
4.一个底面直径是8厘米的圆锥,从顶点沿着高将它切成两半后(如图所示),表面积增加72平方厘米。这个圆锥的体积是多少立方厘米?
5.爸爸从超市买了几盒牛肉罐头。好奇的明明对其中一盒罐头进行了测量,请你根据测量出的数据算出这盒罐头侧面的包装纸的面积。
①我用62.8厘米长的绳子围着罐头的中间刚好绕了两周。 ②我用尺子量得罐头高是6厘米。
6.如图,一张长方形纸片,剪下涂色部分正好围成一个圆柱,求这个圆柱的表面积。
7.我们曾经用下面的方法解决了求三角形面积的问题,有这样的经验,请你求出下面这个几何体的体积。(单位:厘米)
8.下图是一个蛋糕,底盘是泡沫板。(单位:厘米)
(1)请你为这个蛋糕选一个合适的蛋糕盒盖。(在正确答案下面的里画“√”)
(2)这种蛋糕盒盖的上面和侧面都是用透明塑料制作的。制作一个合适的蛋糕盒盖至少需要多少平方厘米的透明塑料?(损耗忽略不计)
9.如图,压路机的前轮是一个圆柱,前轮长1.4米,底面直径是0.8米。如果这台压路机每分钟转25圈,它每分钟可以压多少平方米的路面?
10.如图是一个玩具店出售的一种陀螺。它的上面是圆柱,下面是圆锥。圆柱与圆锥等底等高,圆柱的直径是6厘米,高是4厘米。
(1)这种陀螺的体积是多少立方厘米?
(2)如果给一个这样的陀螺制作一个长方体的包装盒,至少需要多少平方厘米的包装纸?(接头处忽略不计)
参考答案:
1.(1)能;计算过程见详解
(2)31.4米
【分析】
(1)根据圆锥体积=底面积×高÷3,求出沙堆体积,沙堆体积×每立方米重量=沙堆重量,再加上空车质量,与大桥限重比较即可。
(2)根据1米=100厘米,统一单位,路面形状是长方体,根据长方体的长=体积÷(宽×高),列式解答即可。
【详解】
(1)
(立方米)
9.42×1.5=14.13(吨)
14.13+3=17.13(吨)
17.13<20
答:能从西樵大桥上通过。
(2)3厘米=0.03米
9.42÷(10×0.03)
=9.42÷0.3
=31.4(米)
答:能够铺31.4米。
2.369.92立方厘米
【分析】
由图可知,20个这样的钱币垒起来就是一个圆柱体,垒起来的体积=圆柱的体积-长方体的体积,根据圆柱的体积=πr2h,长方体的体积=abh,代入数据解答即可。
【详解】
4毫米=0.4厘米
3.14×(8÷2)2×0.4×20-2×2×0.4×20
=3.14×16×0.4×20-4×0.4×20
=50.24×0.4×20-1.6×20
=20.096×20-32
=401.92-32
=369.92(立方厘米)
答:垒起来的钱币的体积大约是369.92立方厘米。
3.30.144立方米
【分析】
粮囤的体积可以看作是一个圆柱的体积加上一个圆锥的体积,其中圆柱的底面积和圆锥的底面积相等,根据圆柱的体积=底面积×高,圆锥的体积=×底面积×高,代入相应数值计算,据此解答。
【详解】
底面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方米)
(立方米)
答:一个粮囤的体积是30.144立方米。
4.立方厘米
【分析】
将圆锥沿高切成两半后,增加的是两个三角形的面积;其中三角形的底与圆锥底面直径相等,三角形的高与圆锥的高相等;根据三角形的面积=底×高÷2,计算出三角形的高,也就是圆锥的高;最后根据圆锥的体积=πr2h,代入相应数值计算,据此解答。
【详解】
圆锥的高:72÷2×2÷8
=36×2÷8
=72÷8
=9(厘米)
圆锥的体积:
(立方厘米)
答:这个圆锥的体积是150.72立方厘米。
5.188.4平方厘米
【分析】
根据①可知,62.8厘米是罐头底面周长的2倍,那么将62.8厘米除以2,即可求出底面周长。根据②可知,罐头的高是6厘米。根据“圆柱侧面积=底面周长×高”求出这盒罐头侧面的包装纸的面积。
【详解】
62.8÷2×6
=31.4×6
=188.4(平方厘米)
答:这盒罐头侧面的包装纸的面积是188.4平方厘米。
6.282.6平方厘米
【分析】
看图,圆柱的底面周长再加上一条直径是长方形纸片的长。底面周长=3.14×直径,那么将长方形纸片的长除以(3.14+1),即可求出底面直径。圆柱的高是底面直径的2倍,将底面直径乘2,即可求出高。根据“圆柱表面积=底面积×2+侧面积”求出这个圆柱的表面积即可。
【详解】
底面直径:24.84÷(3.14+1)
=24.84÷4.14
=6(厘米)
圆柱的高:6×2=12(厘米)
表面积:3.14×(6÷2)2×2+3.14×6×12
=3.14×32×2+226.08
=3.14×9×2+226.08
=56.52+226.08
=282.6(平方厘米)
答:这个圆柱的表面积是282.6平方厘米。
7.6280立方厘米
【分析】
这个几何体的体积可以看成是一个底面直径为20厘米,高为(15+25)厘米的圆柱体积的一半,根据圆柱的体积=底面积×高,代入相应数值计算,据此解答。
【详解】
3.14×(20÷2)2×(15+25)÷2
=3.14×100×40÷2
=314×40÷2
=12560÷2
=6280(立方厘米)
答:这个几何体的体积是6280立方厘米。
8.(1)见详解
(2)1758.4平方厘米
【分析】1)根据生活中的数学知:蛋糕盒的直径和高度要比蛋糕的直径和高度要大点。由此选择第二个蛋糕盒最合适;
(2)根据圆柱的侧面积=圆的底面周长×高 ,圆柱的底面积=,将数值代入计算即可求得制作这个蛋糕盒盖至少需要多少平方厘米的透明塑料。
【详解】(1)根据生活实际,选第二个蛋糕盒盖合适。
(2)3.14×28×13+3.14×(28÷2)2
=1142.96+3.14×196
=1142.96+615.44
=1758.4(平方厘米)
答:制作一个合适的蛋糕盒盖至少需要1758.4平方厘米的透明塑料。
9.87.92平方米
【分析】压路机前轮滚动一圈所压的路面面积等于圆柱的侧面积,圆柱的侧面积=πdh,前轮滚动一圈所压的面积乘每分钟转动的圈数,即可算出它每分钟可以压的路面面积。
【详解】
(平方米)
答:它每分钟可以压87.92平方米的路面。
10.(1)立方厘米
(2)264平方厘米
【分析】(1)圆柱的直径是6厘米,半径是3厘米,根据圆柱的体积公式,圆锥的体积公式,将数值代入计算后再相加即可。
(2)长方体包装盒的上下底是边长为6厘米的正方形,前后左右四个面是形状一样的长方形,长厘米,宽是6厘米,据此列式解答即可求得包装盒的包装纸。
【详解】(1)(厘米)
=113.04+113.04×
=113.04+37.68
=150.72(立方厘米)
答:这种陀螺的体积是150.72立方厘米。
(2)
=72+192
=264(平方厘米)
答:至少需要264平方厘米的包装纸。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中备考:圆柱与圆锥典型例题与过关练习-数学六年级下册苏教版
典型例题
1.用丝带捆扎下面的圆柱形蛋糕盒,打结处正好是底面圆心,打结用去32厘米长的丝带,捆扎这个蛋糕盒至少用去多少厘米丝带?
2.小东利用两种方法分别测量两个石块的体积:
方法1:利用盛水的容器
方法2:利用橡皮泥,比较裹住石块前后揉成的长方体体积。
(1)这两种方法相同的地方是 。
(2)请选择一种你喜欢的方法计算该石块的体积。
3.如图,以直角三角形的斜边为轴旋转一周,得到一个立体图形,你能算出这个立体图形的体积吗?
4.请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
(1)你选择的材料是( )号和( )号。
(2)你选择的材料一共用了多少平方分米的铁皮?(接头处忽略不计)
(3)你选择的材料做成的水桶最多能装水多少升?
1.172厘米
【分析】
看图,丝带长包括4条底面直径、4条高和打结处的长度,将这三部分的长度相加求出捆扎这个蛋糕盒至少用去多少厘米丝带。
【详解】
20×4+15×4+32
=80+60+32
=172(厘米)
答:捆扎这个蛋糕盒至少用去172厘米丝带。
2.(1)都运用了转化法
(2)一个100.48立方厘米,另一个96立方厘米
【分析】
(1)方法1:将石块的体积转化成圆柱体积进行计算;方法2:将石块的体积转化成长方体体积进行计算。
(2)水面上升的体积就是石块的体积,圆柱底面积×水面上升的高度=石块的体积;橡皮泥前后体积差就是石块的体积,根据长方体体积=长×宽×高,分别求出裹住石块前后的体积,求差即可。
【详解】
(1)这两种方法相同的地方是都运用了转化法。
(2)方法1:3.14×(8÷2)2×(8-6)
=3.14×42×2
=3.14×16×2
=100.48(立方厘米)
方法2:8×4×6-8×2×6
=192-96
=96(立方厘米)
答:一个石块的体积是100.48立方厘米,另一个石块的体积是96立方厘米。
3.241.152立方厘米
【分析】
观察图形可知,以斜边为轴旋转一周,得到的立体图形是上下两个圆锥体,是一个底面半径是(8×6÷2×2÷10)厘米,高的和是10厘米,由此利用圆锥的体积=πr2h,求出两个圆锥的体积再相加,即可解答。
【详解】
底面半径:8×6÷2×2÷10
=48÷2×2÷10
=24×2÷10
=48÷10
=4.8(厘米)
体积:
=×3.14×23.04×10
=×72.3456×10
=24.1152×10
=241.152(立方厘米)
答:这个立体图形的体积241.152立方厘米。
4.(1)①;④
(2)25.905平方分米
(3)14.13升
【分析】
(1)圆柱侧面沿高展开是个长方形,长方形的长或宽等于圆柱底面周长,据此根据圆的周长=圆周率×直径,求出②和④的周长,选择能与之组成圆柱的长方形铁皮即可。
(2)无盖圆柱形水桶只有一个底面,铁皮面积=侧面积+底面积,侧面积=底面周长×高,据此列式解答。
(3)根据圆柱体积=底面积×高,求出水桶容积即可。
【详解】
(1)3.14×4=12.56(分米)
3.14×3=9.42(分米)
选择的材料是①号和④号或②号和③号。
(2)如果选择①号和④号。
9.42×2+3.14×(3÷2)2
=18.84+3.14×1.52
=18.84+3.14×2.25
=18.84+7.065
=25.905(平方分米)
如果选择②号和③号。
12.56×5+3.14×(4÷2)2
=62.8+3.14×22
=62.8+3.14×4
=62.8+12.56
=75.36(平方分米)
答:如果选择①号和④号一共用了25.905平方分米的铁皮;如果选择②号和③号一共用了75.36平方分米的铁皮
(3)如果选择①号和④号。
3.14×(3÷2)2×2
=3.14×1.52×2
=3.14×2.25×2
=14.13(立方分米)
=14.13(升)
如果选择②号和③号。
3.14×(4÷2)2×5
=3.14×22×5
=3.14×4×5
=62.8(立方分米)
=62.8(升)
答:如果选择①号和④号做成的水桶最多能装水14.13升;如果选择②号和③号做成的水桶最多能装水62.8升。
过关练习
1.一个圆锥形沙堆,底面直径为6米,高是1米,每立方米的沙子重1.5吨。
西樵大桥禁止20吨以上车辆通行,过往车辆请绕道行驶。
(1)林叔叔用一辆空车质量是3吨的卡车一次性运走这堆沙子,能从西樵大桥上通过吗?(写出计算过程)
(2)用这堆沙子在10米宽的公路上铺3厘米厚的路面,能够铺多少米?
2.元代的一种圆形钱币(如图)直径约为8厘米,厚度为4毫米,正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来,求垒起来的钱币的体积大约是多少立方厘米?
3.如图,粮囤上面是圆锥形,下面是圆柱形,圆柱的底面周长是12.56米,高是2米,圆锥的高是1.2米。一个粮囤的体积是多少立方米?
4.一个底面直径是8厘米的圆锥,从顶点沿着高将它切成两半后(如图所示),表面积增加72平方厘米。这个圆锥的体积是多少立方厘米?
5.爸爸从超市买了几盒牛肉罐头。好奇的明明对其中一盒罐头进行了测量,请你根据测量出的数据算出这盒罐头侧面的包装纸的面积。
①我用62.8厘米长的绳子围着罐头的中间刚好绕了两周。 ②我用尺子量得罐头高是6厘米。
6.如图,一张长方形纸片,剪下涂色部分正好围成一个圆柱,求这个圆柱的表面积。
7.我们曾经用下面的方法解决了求三角形面积的问题,有这样的经验,请你求出下面这个几何体的体积。(单位:厘米)
8.下图是一个蛋糕,底盘是泡沫板。(单位:厘米)
(1)请你为这个蛋糕选一个合适的蛋糕盒盖。(在正确答案下面的里画“√”)
(2)这种蛋糕盒盖的上面和侧面都是用透明塑料制作的。制作一个合适的蛋糕盒盖至少需要多少平方厘米的透明塑料?(损耗忽略不计)
9.如图,压路机的前轮是一个圆柱,前轮长1.4米,底面直径是0.8米。如果这台压路机每分钟转25圈,它每分钟可以压多少平方米的路面?
10.如图是一个玩具店出售的一种陀螺。它的上面是圆柱,下面是圆锥。圆柱与圆锥等底等高,圆柱的直径是6厘米,高是4厘米。
(1)这种陀螺的体积是多少立方厘米?
(2)如果给一个这样的陀螺制作一个长方体的包装盒,至少需要多少平方厘米的包装纸?(接头处忽略不计)
参考答案:
1.(1)能;计算过程见详解
(2)31.4米
【分析】
(1)根据圆锥体积=底面积×高÷3,求出沙堆体积,沙堆体积×每立方米重量=沙堆重量,再加上空车质量,与大桥限重比较即可。
(2)根据1米=100厘米,统一单位,路面形状是长方体,根据长方体的长=体积÷(宽×高),列式解答即可。
【详解】
(1)
(立方米)
9.42×1.5=14.13(吨)
14.13+3=17.13(吨)
17.13<20
答:能从西樵大桥上通过。
(2)3厘米=0.03米
9.42÷(10×0.03)
=9.42÷0.3
=31.4(米)
答:能够铺31.4米。
2.369.92立方厘米
【分析】
由图可知,20个这样的钱币垒起来就是一个圆柱体,垒起来的体积=圆柱的体积-长方体的体积,根据圆柱的体积=πr2h,长方体的体积=abh,代入数据解答即可。
【详解】
4毫米=0.4厘米
3.14×(8÷2)2×0.4×20-2×2×0.4×20
=3.14×16×0.4×20-4×0.4×20
=50.24×0.4×20-1.6×20
=20.096×20-32
=401.92-32
=369.92(立方厘米)
答:垒起来的钱币的体积大约是369.92立方厘米。
3.30.144立方米
【分析】
粮囤的体积可以看作是一个圆柱的体积加上一个圆锥的体积,其中圆柱的底面积和圆锥的底面积相等,根据圆柱的体积=底面积×高,圆锥的体积=×底面积×高,代入相应数值计算,据此解答。
【详解】
底面积:3.14×(12.56÷3.14÷2)2
=3.14×(4÷2)2
=3.14×4
=12.56(平方米)
(立方米)
答:一个粮囤的体积是30.144立方米。
4.立方厘米
【分析】
将圆锥沿高切成两半后,增加的是两个三角形的面积;其中三角形的底与圆锥底面直径相等,三角形的高与圆锥的高相等;根据三角形的面积=底×高÷2,计算出三角形的高,也就是圆锥的高;最后根据圆锥的体积=πr2h,代入相应数值计算,据此解答。
【详解】
圆锥的高:72÷2×2÷8
=36×2÷8
=72÷8
=9(厘米)
圆锥的体积:
(立方厘米)
答:这个圆锥的体积是150.72立方厘米。
5.188.4平方厘米
【分析】
根据①可知,62.8厘米是罐头底面周长的2倍,那么将62.8厘米除以2,即可求出底面周长。根据②可知,罐头的高是6厘米。根据“圆柱侧面积=底面周长×高”求出这盒罐头侧面的包装纸的面积。
【详解】
62.8÷2×6
=31.4×6
=188.4(平方厘米)
答:这盒罐头侧面的包装纸的面积是188.4平方厘米。
6.282.6平方厘米
【分析】
看图,圆柱的底面周长再加上一条直径是长方形纸片的长。底面周长=3.14×直径,那么将长方形纸片的长除以(3.14+1),即可求出底面直径。圆柱的高是底面直径的2倍,将底面直径乘2,即可求出高。根据“圆柱表面积=底面积×2+侧面积”求出这个圆柱的表面积即可。
【详解】
底面直径:24.84÷(3.14+1)
=24.84÷4.14
=6(厘米)
圆柱的高:6×2=12(厘米)
表面积:3.14×(6÷2)2×2+3.14×6×12
=3.14×32×2+226.08
=3.14×9×2+226.08
=56.52+226.08
=282.6(平方厘米)
答:这个圆柱的表面积是282.6平方厘米。
7.6280立方厘米
【分析】
这个几何体的体积可以看成是一个底面直径为20厘米,高为(15+25)厘米的圆柱体积的一半,根据圆柱的体积=底面积×高,代入相应数值计算,据此解答。
【详解】
3.14×(20÷2)2×(15+25)÷2
=3.14×100×40÷2
=314×40÷2
=12560÷2
=6280(立方厘米)
答:这个几何体的体积是6280立方厘米。
8.(1)见详解
(2)1758.4平方厘米
【分析】1)根据生活中的数学知:蛋糕盒的直径和高度要比蛋糕的直径和高度要大点。由此选择第二个蛋糕盒最合适;
(2)根据圆柱的侧面积=圆的底面周长×高 ,圆柱的底面积=,将数值代入计算即可求得制作这个蛋糕盒盖至少需要多少平方厘米的透明塑料。
【详解】(1)根据生活实际,选第二个蛋糕盒盖合适。
(2)3.14×28×13+3.14×(28÷2)2
=1142.96+3.14×196
=1142.96+615.44
=1758.4(平方厘米)
答:制作一个合适的蛋糕盒盖至少需要1758.4平方厘米的透明塑料。
9.87.92平方米
【分析】压路机前轮滚动一圈所压的路面面积等于圆柱的侧面积,圆柱的侧面积=πdh,前轮滚动一圈所压的面积乘每分钟转动的圈数,即可算出它每分钟可以压的路面面积。
【详解】
(平方米)
答:它每分钟可以压87.92平方米的路面。
10.(1)立方厘米
(2)264平方厘米
【分析】(1)圆柱的直径是6厘米,半径是3厘米,根据圆柱的体积公式,圆锥的体积公式,将数值代入计算后再相加即可。
(2)长方体包装盒的上下底是边长为6厘米的正方形,前后左右四个面是形状一样的长方形,长厘米,宽是6厘米,据此列式解答即可求得包装盒的包装纸。
【详解】(1)(厘米)
=113.04+113.04×
=113.04+37.68
=150.72(立方厘米)
答:这种陀螺的体积是150.72立方厘米。
(2)
=72+192
=264(平方厘米)
答:至少需要264平方厘米的包装纸。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
