第三十章 提升拔高 二次函数图像的交点问题 习题课件(共18张PPT)2023-2024学年冀教版数学九年级下册
文档属性
| 名称 | 第三十章 提升拔高 二次函数图像的交点问题 习题课件(共18张PPT)2023-2024学年冀教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 760.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览


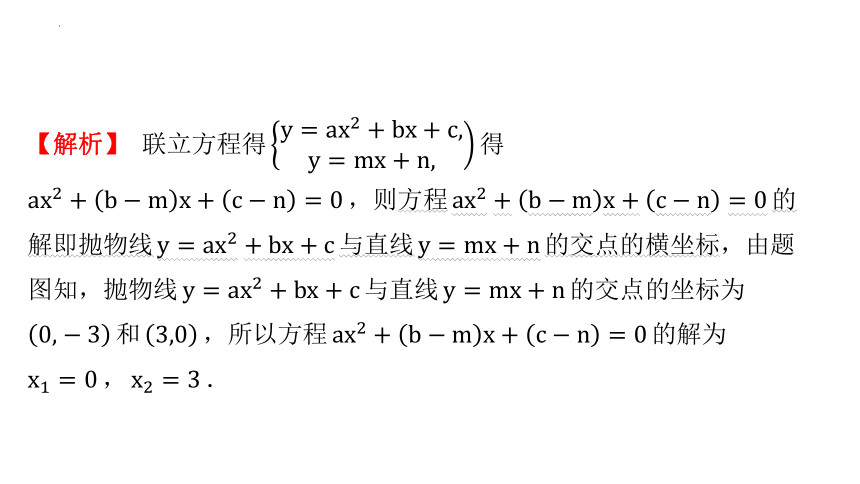




文档简介
(共18张PPT)
第三十章 二次函数
专项4 二次函数图像的交点问题
过专项 阶段强化专项训练
类型1 直线与抛物线的交点问题
第1题图
1.[2023衡水桃城中学期末]在平面直角坐标系中,
抛物线 与直线 如
图所示,方程 的
解为( )
A
A. , B. ,
C. , D. ,
【解析】 联立方程得 得
,则方程 的
解即抛物线 与直线 的交点的横坐标,由题
图知,抛物线 与直线 的交点的坐标为
和 ,所以方程 的解为
, .
第2题图
2.[2021广元中考]将二次函数 的图像
在 轴上方的部分沿 轴翻折后,所得新函数的图像如
图所示.当直线 与新函数的图像恰有3个公共
点时, 的值为( )
A
A. 或 B. 或
C. 或 D. 或
【解析】 二次函数的表达式为
, 抛物线
的顶点坐标为 .当 时,
,解得 , ,如图,则
抛物线 与 轴的交点为 ,
.把抛物线 在 轴上方的部分
沿 轴翻折到 轴下方,则翻折后所得中间部分的抛
物线的表达式为 ,顶点坐标为 .当直
线 过点 时,直线 与该新图像恰好有3个公共点,
,解得 .当直线 与抛物线
相切时,直线 与该新图像恰好有
3个公共点,此时 有两个相等的实数解,整理得
, ,解得 .综上所
述, 的值为 或 .
类型2 线段与抛物线的交点问题
3.[2023贵州师范大学贵阳附属初级中学一模]如图,在平面
直角坐标系中,点 的坐标为 ,点 的坐标为 ,
若抛物线 与线段 有公共点,则 的
取值范围为( )
C
A. B.
C. D. 或
【解析】 如图,
当抛物线过点 时,将 的坐标代入
中,解得 ;当抛物线过点 时,
将 的坐标代入 中,解得
, , 直线 的表达式为
.当抛物线与线段 只有一个公共点时,方程
有两个相等的实数根,则 ,解
得 . 当 时,抛物线与线段 有一个公共点,随着 的增大,
抛物线沿竖直方向向上平移;当 时,抛物线与线段 始终有
公共点;当 时,抛物线与线段 有一个公共点.综上所述,抛物
线 与线段 有公共点, 的取值范围为
.
4.对于题目:在平面直角坐标系中,直线 分别与 轴、 轴交
于点 , ,过点 且平行于 轴的直线与过点 且平行于 轴的直线相
交于点 ,若抛物线 与线段 有唯一公共点,
求 的取值范围.甲的计算结果是 ,乙的计算结果是 ,则
( )
D
A.甲的结果正确 B.乙的结果正确
C.甲与乙的结果合在一起正确 D.甲与乙的结果合在一起也不正确
【解析】 对于 ,
令 ,则 或3,令 ,
则 ,所以抛物线与 轴的
交点坐标分别为 , ,与
轴的交点坐标为 .抛物线
的对称轴为直
线 ,顶点坐标为 ,因为直线 分别与 轴、
轴交于点 , ,所以点 , 的坐标分别为 , ,所以点 的
坐标为 .(1)若 ,如图1,当抛物线过点 时,抛物线与线段
有一个公共点,将点 的坐标代入抛物线的表达式,得
,解得 ,结合图像可知,当抛物线与线段 有唯一公共点时,
.(2)若 ,当抛物线的顶点在线段 上时,抛物线与 有
唯一公共点,此时 ,解得 ;如图2,当抛物线过点 时,抛
物线与 有两个交点,将点 的坐标代入抛物线的表达式,
得 ,解得 ,结合图像可知,当
抛物线与线段 有唯一公共点时, ,故当 时,满足题意
的 的取值范围为 或 .综上, 的取值范围为 或
或 .
类型3 整点问题
5.[2023石家庄藁城区二模]已知抛物线
, 均为常数,
且 , 交 轴于点 ,点 在抛
物线 上,连接 ,且 平行于 轴.
(1)用 表示 ,并求抛物线 的对称轴及 点坐标;
解: 轴,点 、点 在抛物线 上,
点 、点 关于抛物线的对称轴对称,
抛物线 的对称轴为直线 , , ,
在抛物线上,
, .
(2)当抛物线 经过 时,求 的表达式及其顶点坐标;
抛物线 经过点 , ,
解得
的表达式为 ,
顶点坐标为 .
(3)如果把横、纵坐标都是整数的点叫做“整点”,如图,当 时,
若抛物线 位于线段 下方的部分与线段 所围成的区域内(不含边
界)恰有5个“整点”,求 的取值范围.
由(1)知 ,
抛物线的表达式为 ,
顶点坐标为 ,
抛物线 位于线段 下方的部分与线段 所围成的区域内(不含边
界)恰有5个“整点”, , ,
符合题意的整点都在直线 上,符合题意的整点为 ,
, , , ,
, .
第三十章 二次函数
专项4 二次函数图像的交点问题
过专项 阶段强化专项训练
类型1 直线与抛物线的交点问题
第1题图
1.[2023衡水桃城中学期末]在平面直角坐标系中,
抛物线 与直线 如
图所示,方程 的
解为( )
A
A. , B. ,
C. , D. ,
【解析】 联立方程得 得
,则方程 的
解即抛物线 与直线 的交点的横坐标,由题
图知,抛物线 与直线 的交点的坐标为
和 ,所以方程 的解为
, .
第2题图
2.[2021广元中考]将二次函数 的图像
在 轴上方的部分沿 轴翻折后,所得新函数的图像如
图所示.当直线 与新函数的图像恰有3个公共
点时, 的值为( )
A
A. 或 B. 或
C. 或 D. 或
【解析】 二次函数的表达式为
, 抛物线
的顶点坐标为 .当 时,
,解得 , ,如图,则
抛物线 与 轴的交点为 ,
.把抛物线 在 轴上方的部分
沿 轴翻折到 轴下方,则翻折后所得中间部分的抛
物线的表达式为 ,顶点坐标为 .当直
线 过点 时,直线 与该新图像恰好有3个公共点,
,解得 .当直线 与抛物线
相切时,直线 与该新图像恰好有
3个公共点,此时 有两个相等的实数解,整理得
, ,解得 .综上所
述, 的值为 或 .
类型2 线段与抛物线的交点问题
3.[2023贵州师范大学贵阳附属初级中学一模]如图,在平面
直角坐标系中,点 的坐标为 ,点 的坐标为 ,
若抛物线 与线段 有公共点,则 的
取值范围为( )
C
A. B.
C. D. 或
【解析】 如图,
当抛物线过点 时,将 的坐标代入
中,解得 ;当抛物线过点 时,
将 的坐标代入 中,解得
, , 直线 的表达式为
.当抛物线与线段 只有一个公共点时,方程
有两个相等的实数根,则 ,解
得 . 当 时,抛物线与线段 有一个公共点,随着 的增大,
抛物线沿竖直方向向上平移;当 时,抛物线与线段 始终有
公共点;当 时,抛物线与线段 有一个公共点.综上所述,抛物
线 与线段 有公共点, 的取值范围为
.
4.对于题目:在平面直角坐标系中,直线 分别与 轴、 轴交
于点 , ,过点 且平行于 轴的直线与过点 且平行于 轴的直线相
交于点 ,若抛物线 与线段 有唯一公共点,
求 的取值范围.甲的计算结果是 ,乙的计算结果是 ,则
( )
D
A.甲的结果正确 B.乙的结果正确
C.甲与乙的结果合在一起正确 D.甲与乙的结果合在一起也不正确
【解析】 对于 ,
令 ,则 或3,令 ,
则 ,所以抛物线与 轴的
交点坐标分别为 , ,与
轴的交点坐标为 .抛物线
的对称轴为直
线 ,顶点坐标为 ,因为直线 分别与 轴、
轴交于点 , ,所以点 , 的坐标分别为 , ,所以点 的
坐标为 .(1)若 ,如图1,当抛物线过点 时,抛物线与线段
有一个公共点,将点 的坐标代入抛物线的表达式,得
,解得 ,结合图像可知,当抛物线与线段 有唯一公共点时,
.(2)若 ,当抛物线的顶点在线段 上时,抛物线与 有
唯一公共点,此时 ,解得 ;如图2,当抛物线过点 时,抛
物线与 有两个交点,将点 的坐标代入抛物线的表达式,
得 ,解得 ,结合图像可知,当
抛物线与线段 有唯一公共点时, ,故当 时,满足题意
的 的取值范围为 或 .综上, 的取值范围为 或
或 .
类型3 整点问题
5.[2023石家庄藁城区二模]已知抛物线
, 均为常数,
且 , 交 轴于点 ,点 在抛
物线 上,连接 ,且 平行于 轴.
(1)用 表示 ,并求抛物线 的对称轴及 点坐标;
解: 轴,点 、点 在抛物线 上,
点 、点 关于抛物线的对称轴对称,
抛物线 的对称轴为直线 , , ,
在抛物线上,
, .
(2)当抛物线 经过 时,求 的表达式及其顶点坐标;
抛物线 经过点 , ,
解得
的表达式为 ,
顶点坐标为 .
(3)如果把横、纵坐标都是整数的点叫做“整点”,如图,当 时,
若抛物线 位于线段 下方的部分与线段 所围成的区域内(不含边
界)恰有5个“整点”,求 的取值范围.
由(1)知 ,
抛物线的表达式为 ,
顶点坐标为 ,
抛物线 位于线段 下方的部分与线段 所围成的区域内(不含边
界)恰有5个“整点”, , ,
符合题意的整点都在直线 上,符合题意的整点为 ,
, , , ,
, .
