10.5用二元一次方程组解决问题—几何图形问题 专题提升训练(含解析) 苏科版七年级数学下册
文档属性
| 名称 | 10.5用二元一次方程组解决问题—几何图形问题 专题提升训练(含解析) 苏科版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 264.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 06:46:16 | ||
图片预览

文档简介
苏科版七年级数学下册《10.5用二元一次方程组解决问题—几何图形问题》专题提升训练(附答案)
一、单选题
1.如图,一幅宣传画的四周镶嵌宽度为m的花边,镶好后整幅作品的周长比宣传画的周长多16,面积比宣传画的面积大32,则宣传画的周长是( )
A.16 B.8 C.4 D.
2.如图,将四个形状,大小相同的长方形拼成一个大的长方形,如果大长方形的周长为 ,那么大长方形的面积是( )
A. B. C. D.
3.一副三角板按如图方式摆放,且的度数比的度数大,则( )
A. B. C. D.
4.如图,ABCD为一长条形纸带,,将ABCD沿EF折叠,A,D两点分别与,对应,若,设,,根据题意可得( )
A. B. C. D.
5.如图,在长为20m,宽为16m的长方形空地中,沿平行于长方形各边的方向修建三个相同的小长方形花圃,则每个小长方形的面积是( )
A.24m2 B.32m2
C.40m2 D.48m2
6.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高,两块横放的墙砖比两块竖放的墙砖低,则每块墙砖的截面面积是( )
A. B. C. D.
7.个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为厘米的小正方形.设一个小长方形的长为厘米,宽为厘米,则所列二元一次方程组正确的是( )
A. B. C. D.
二、填空题
8.如图所示为两个形状、大小一样的小长方形拼接而成的图形.已知.则小长方形的面积为 .
9.《九章算术》是我国东汉初年编订的一部数学经典著作,其中一次方程组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是,类似的,图(2)所示的算筹图用方程组表示出来,就是 .
10.如图,直线与相交于点O,且,比大,设,则可列方程组为 .
11.已知,x、y分别为小正方形和大正方形的边长,则阴影部分面积为 .
12.如下图,把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放,设大长方形长为x cm,小长方形长为y cm.根据题意,可列方程组 .
13.如图,在长方形中,放入6个形状、大小都相同的长方形,所标尺寸如图所示,则图中阴影部分面积是 ,若平移这六个长方形,则图中剩余的阴影部分面积是否改变? (填“变”或“不变”).
14.如图,AB∥CD,AD∥BC,点E在AD边上,连接BE,使得∠BAE=∠BEA,连接CE并延长与BA延长线交于点F,若∠F+∠BEC=92°,则∠BCE= .
三、解答题
15.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为,求重叠部分面积.
16.如图1,在边长为a的大正方形中剪去一个边长为b的小正方形.
(1)若,分别求S1,S2的面积;
(2)若将图1的阴影部分沿虚线剪开,重新拼成图2的长方形,且长为,宽为,求S1∶S2的值.
17.钟山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米,现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米.
(1)整改后A园区的长为 ,宽为 ;(用代数式表示)
(2)若整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米,求x、y的值.
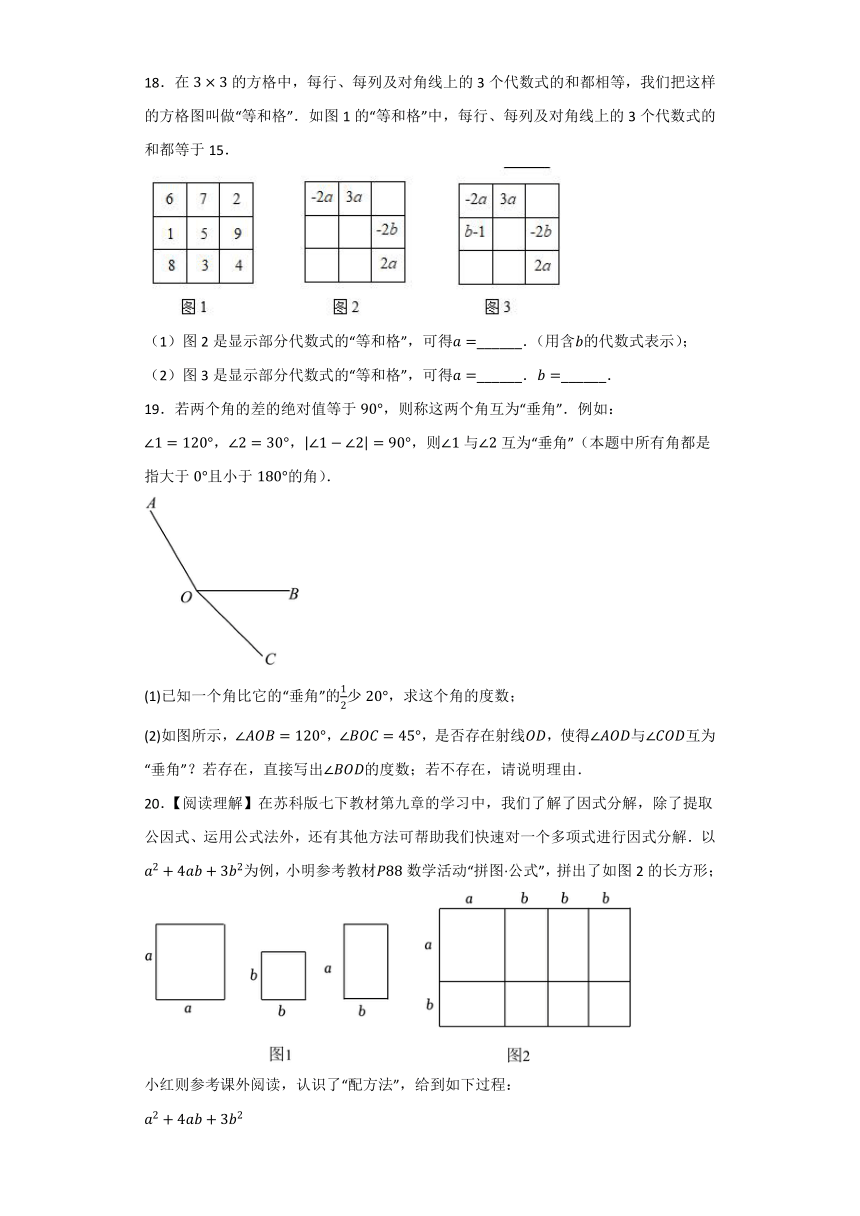
18.在的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得______.(用含的代数式表示);
(2)图3是显示部分代数式的“等和格”,可得______.______.
19.若两个角的差的绝对值等于,则称这两个角互为“垂角”.例如:
,,,则与互为“垂角”(本题中所有角都是指大于且小于的角).
(1)已知一个角比它的“垂角”的少,求这个角的度数;
(2)如图所示,,,是否存在射线,使得与互为“垂角”?若存在,直接写出的度数;若不存在,请说明理由.
20.【阅读理解】在苏科版七下教材第九章的学习中,我们了解了因式分解,除了提取公因式、运用公式法外,还有其他方法可帮助我们快速对一个多项式进行因式分解.以为例,小明参考教材数学活动“拼图公式”,拼出了如图2的长方形;
小红则参考课外阅读,认识了“配方法”,给到如下过程:
,
,
,
【尝试解决】
(1)由拼图可得等式 ;
(2)请接着小红的思路补全解答过程;
(3)上述两种方法,任选一种将因式分解.(注:若选择拼图法,请画出图形,并做适当标注;若选配方法,请写完整过程)
(4)【实际应用】学校有一长方形空地,为了美化校园环境,现欲规划1块型、6块型正方形和5块型小长方形区域、都是正整数),种植不同种类的花草.若长方形空地总面积为,求出、的值分别是多少?
参考答案
1.解:设宣传画的一边长为x,另一边长为y,
则,
,
故选:B.
2.解:设小成方形长为a宽为b,由题意可得,
,
解得:,
大长方形的面积是:,
故选C.
3.解:由题意,可得:,
解得:,
故选:C
4.解:根据题意,得 .
故选:A.
5.解:设小长方形的长为xm,宽为ym,
则根据图形可得,
解得,
∴小长方形的面积为:48=32m.
故选B.
6.解:设每块墙砖的长为,宽为,
根据题意得:,
解得:
∴每块墙砖的截面面积:,
故选:C
7.解:在甲图中, 个小长方形的长个小长方形的宽,在乙图中,个小长方形的宽个长方形的长厘米,可得
故选:A.
8.解:设小长方形的长为x,宽为y,
依题意得:
解得:
∴,
∴小长方形的面积为4.
故答案为:4.
9.解:由图1可得,第一列为x的系数、第二列为y的系数,第三列和第四列为方程右边的常数,且前两列一竖表示1,第三列一横表示10,第四列一竖表示1,一横表示5
则根据图2可得:.
故填.
10.解:由题意得,
故答案为:.
11.解:
∴
解得
则阴影部分面积为:大正方形的面积-小正方形的面积
即:
故答案为:10
12.解: 根据题意得:,
故答案为:.
13.解:设每个长方形的长为xcm,宽为ycm,则有方程组:
解得:
所以大长方形的宽为:7+2×3=13(cm),其面积为13×19=247(cm2),一个小长方形的面积为3×10=30(cm2)
所以阴影部分的面积为:247-6×30=67(cm2)
由于平移不改变图形的面积,故这六个小长方形的总面积不变,又大长方形的面积一定,所以阴影部分的面积不变.
故答案为:67cm2;不变.
14.解:设,
∵
∴,
∵,
∴设,
则,
在中,
,
在中,利用三角形内角和定理可得:
,
即,
解得:,
∴,
故答案为:.
15.解:设大长方形的面积为,小长方形的面积为,根据题意得,
解得:
∴重叠面积为
16.(1)解:由题意得:,
(2)解:由题意得:,
∴
由(1)得,
∴
17.(1)解:整改后A园区的长为:x+y+11x﹣y=12x(米),
宽为:x﹣y﹣(x﹣2y)=y(米),
故答案为:12x米,y米;
(2)依题意有:
,
解得.
18.解:(1)由题意得:,
则,
故.
(2)由题意得:,
解得,
由(1)得,
则.
19.解:(1)设这个角为,它的垂角为,
根据题意,得,
解得:,
故这个角的度数为;
(2)的度数为:或或,
理由如下:分两种情况:
在的内部时,
,
解得或,
∴或;
②在外部时,
,
解得或,
∴或(舍去),
故的度数为:或或.
20.(1)解:由图可得:;
故答案为:;
(2)解:补全解答过程:
,
,
,
;
(3)解:配方法:
;
拼图法:
可得;
(4)解:由(3)知,,
,都是正整数,
或,
解得(舍去)或,
答:的值为1,的值为2.
一、单选题
1.如图,一幅宣传画的四周镶嵌宽度为m的花边,镶好后整幅作品的周长比宣传画的周长多16,面积比宣传画的面积大32,则宣传画的周长是( )
A.16 B.8 C.4 D.
2.如图,将四个形状,大小相同的长方形拼成一个大的长方形,如果大长方形的周长为 ,那么大长方形的面积是( )
A. B. C. D.
3.一副三角板按如图方式摆放,且的度数比的度数大,则( )
A. B. C. D.
4.如图,ABCD为一长条形纸带,,将ABCD沿EF折叠,A,D两点分别与,对应,若,设,,根据题意可得( )
A. B. C. D.
5.如图,在长为20m,宽为16m的长方形空地中,沿平行于长方形各边的方向修建三个相同的小长方形花圃,则每个小长方形的面积是( )
A.24m2 B.32m2
C.40m2 D.48m2
6.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高,两块横放的墙砖比两块竖放的墙砖低,则每块墙砖的截面面积是( )
A. B. C. D.
7.个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,若拼成如图乙所示的正方形,中间还留下一个洞,恰好是边长为厘米的小正方形.设一个小长方形的长为厘米,宽为厘米,则所列二元一次方程组正确的是( )
A. B. C. D.
二、填空题
8.如图所示为两个形状、大小一样的小长方形拼接而成的图形.已知.则小长方形的面积为 .
9.《九章算术》是我国东汉初年编订的一部数学经典著作,其中一次方程组是用算筹布置而成,如图(1)所示的算筹图用我们现在所熟悉的方程组表示出来,就是,类似的,图(2)所示的算筹图用方程组表示出来,就是 .
10.如图,直线与相交于点O,且,比大,设,则可列方程组为 .
11.已知,x、y分别为小正方形和大正方形的边长,则阴影部分面积为 .
12.如下图,把长都是宽的两倍的1个大长方形纸片和4个相同的小长方形纸片按图①、图②方式摆放,设大长方形长为x cm,小长方形长为y cm.根据题意,可列方程组 .
13.如图,在长方形中,放入6个形状、大小都相同的长方形,所标尺寸如图所示,则图中阴影部分面积是 ,若平移这六个长方形,则图中剩余的阴影部分面积是否改变? (填“变”或“不变”).
14.如图,AB∥CD,AD∥BC,点E在AD边上,连接BE,使得∠BAE=∠BEA,连接CE并延长与BA延长线交于点F,若∠F+∠BEC=92°,则∠BCE= .
三、解答题
15.如图所示,两个长方形重叠部分的面积相当于大长方形面积的六分之一,相当于小长方形面积的四分之一,阴影部分的面积为,求重叠部分面积.
16.如图1,在边长为a的大正方形中剪去一个边长为b的小正方形.
(1)若,分别求S1,S2的面积;
(2)若将图1的阴影部分沿虚线剪开,重新拼成图2的长方形,且长为,宽为,求S1∶S2的值.
17.钟山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米,现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米.
(1)整改后A园区的长为 ,宽为 ;(用代数式表示)
(2)若整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米,求x、y的值.
18.在的方格中,每行、每列及对角线上的3个代数式的和都相等,我们把这样的方格图叫做“等和格”.如图1的“等和格”中,每行、每列及对角线上的3个代数式的和都等于15.
(1)图2是显示部分代数式的“等和格”,可得______.(用含的代数式表示);
(2)图3是显示部分代数式的“等和格”,可得______.______.
19.若两个角的差的绝对值等于,则称这两个角互为“垂角”.例如:
,,,则与互为“垂角”(本题中所有角都是指大于且小于的角).
(1)已知一个角比它的“垂角”的少,求这个角的度数;
(2)如图所示,,,是否存在射线,使得与互为“垂角”?若存在,直接写出的度数;若不存在,请说明理由.
20.【阅读理解】在苏科版七下教材第九章的学习中,我们了解了因式分解,除了提取公因式、运用公式法外,还有其他方法可帮助我们快速对一个多项式进行因式分解.以为例,小明参考教材数学活动“拼图公式”,拼出了如图2的长方形;
小红则参考课外阅读,认识了“配方法”,给到如下过程:
,
,
,
【尝试解决】
(1)由拼图可得等式 ;
(2)请接着小红的思路补全解答过程;
(3)上述两种方法,任选一种将因式分解.(注:若选择拼图法,请画出图形,并做适当标注;若选配方法,请写完整过程)
(4)【实际应用】学校有一长方形空地,为了美化校园环境,现欲规划1块型、6块型正方形和5块型小长方形区域、都是正整数),种植不同种类的花草.若长方形空地总面积为,求出、的值分别是多少?
参考答案
1.解:设宣传画的一边长为x,另一边长为y,
则,
,
故选:B.
2.解:设小成方形长为a宽为b,由题意可得,
,
解得:,
大长方形的面积是:,
故选C.
3.解:由题意,可得:,
解得:,
故选:C
4.解:根据题意,得 .
故选:A.
5.解:设小长方形的长为xm,宽为ym,
则根据图形可得,
解得,
∴小长方形的面积为:48=32m.
故选B.
6.解:设每块墙砖的长为,宽为,
根据题意得:,
解得:
∴每块墙砖的截面面积:,
故选:C
7.解:在甲图中, 个小长方形的长个小长方形的宽,在乙图中,个小长方形的宽个长方形的长厘米,可得
故选:A.
8.解:设小长方形的长为x,宽为y,
依题意得:
解得:
∴,
∴小长方形的面积为4.
故答案为:4.
9.解:由图1可得,第一列为x的系数、第二列为y的系数,第三列和第四列为方程右边的常数,且前两列一竖表示1,第三列一横表示10,第四列一竖表示1,一横表示5
则根据图2可得:.
故填.
10.解:由题意得,
故答案为:.
11.解:
∴
解得
则阴影部分面积为:大正方形的面积-小正方形的面积
即:
故答案为:10
12.解: 根据题意得:,
故答案为:.
13.解:设每个长方形的长为xcm,宽为ycm,则有方程组:
解得:
所以大长方形的宽为:7+2×3=13(cm),其面积为13×19=247(cm2),一个小长方形的面积为3×10=30(cm2)
所以阴影部分的面积为:247-6×30=67(cm2)
由于平移不改变图形的面积,故这六个小长方形的总面积不变,又大长方形的面积一定,所以阴影部分的面积不变.
故答案为:67cm2;不变.
14.解:设,
∵
∴,
∵,
∴设,
则,
在中,
,
在中,利用三角形内角和定理可得:
,
即,
解得:,
∴,
故答案为:.
15.解:设大长方形的面积为,小长方形的面积为,根据题意得,
解得:
∴重叠面积为
16.(1)解:由题意得:,
(2)解:由题意得:,
∴
由(1)得,
∴
17.(1)解:整改后A园区的长为:x+y+11x﹣y=12x(米),
宽为:x﹣y﹣(x﹣2y)=y(米),
故答案为:12x米,y米;
(2)依题意有:
,
解得.
18.解:(1)由题意得:,
则,
故.
(2)由题意得:,
解得,
由(1)得,
则.
19.解:(1)设这个角为,它的垂角为,
根据题意,得,
解得:,
故这个角的度数为;
(2)的度数为:或或,
理由如下:分两种情况:
在的内部时,
,
解得或,
∴或;
②在外部时,
,
解得或,
∴或(舍去),
故的度数为:或或.
20.(1)解:由图可得:;
故答案为:;
(2)解:补全解答过程:
,
,
,
;
(3)解:配方法:
;
拼图法:
可得;
(4)解:由(3)知,,
,都是正整数,
或,
解得(舍去)或,
答:的值为1,的值为2.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
