北师大版数学七年级下册期中测试卷.(含答案)
文档属性
| 名称 | 北师大版数学七年级下册期中测试卷.(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 08:01:17 | ||
图片预览


文档简介
北师大数学七年级下数学七年级下学期期中测试卷.
(满分120分)
一、选择题(每小题3分,共30分)
1.下列计算结果正确的是( )
A.2a3+a3=3a6 B.(-a)2·a3=-a6 C.()-2=4 D.(-2)0=-1
2.下列各式中,不能用平方差公式计算的是( )
A.(-4x+3y)(4x+3y) B.(4x-3y)(3y-4x)
C.(-4x+3y)(-4x-3y) D.(4x+3y)(4x-3y)
3.下列计算中,正确的是( )
A.3a3·2a2=6a6 B.2x2·3x2=6x4
C.3x2·4x2=12x2 D.5a3·3a5=15a15
4.已知a+b=3,ab=2,则a2+b2+ab的值为( )
A.5 B.7 C.9 D.13
5.若am=12,an=3,则am-n=( )
A.4 B.9 C.15 D.36
6.如图所示,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD与∠1互为补角 D.∠1的余角等于75°30′
7.如图,AF是∠BAC的平分线,EF//AC交AB于点E,若∠1=25°,则∠BAF的度数为( )
A.15° B.50° C.25° D.12.5°
8.一条公路两次转弯后又回到原来的方向(即AB//CD),如图所示,如果第一次转弯时∠B=140°,那么∠C应等于( )
A.140° B.40° C.100° D.180°
9.关于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是自变量,2是常量
B.C是因变量,R是自变量,2,π是常量
C.R是自变量,2,π,C是常量
D.C是自变量,R是因变量,2,π是常量
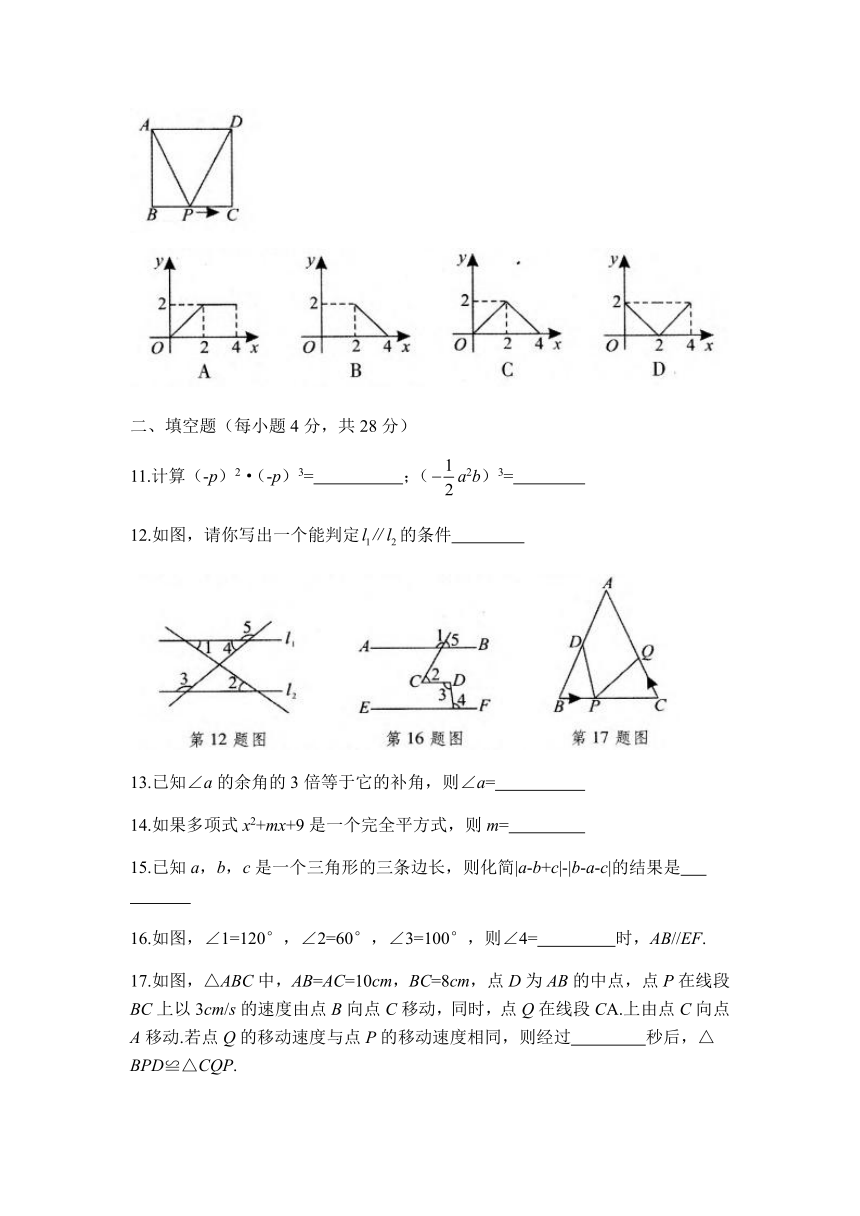
10.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
二、填空题(每小题4分,共28分)
11.计算(-p)2·(-p)3= ;(a2b)3=
12.如图,请你写出一个能判定的条件
13.已知∠a的余角的3倍等于它的补角,则∠a=
14.如果多项式x2+mx+9是一个完全平方式,则m=
15.已知a,b,c是一个三角形的三条边长,则化简|a-b+c|-|b-a-c|的结果是
16.如图,∠1=120°,∠2=60°,∠3=100°,则∠4= 时,AB//EF.
17.如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA.上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过 秒后,△BPD≌△CQP.
三、解答题(一)(每小题6分,共18分)
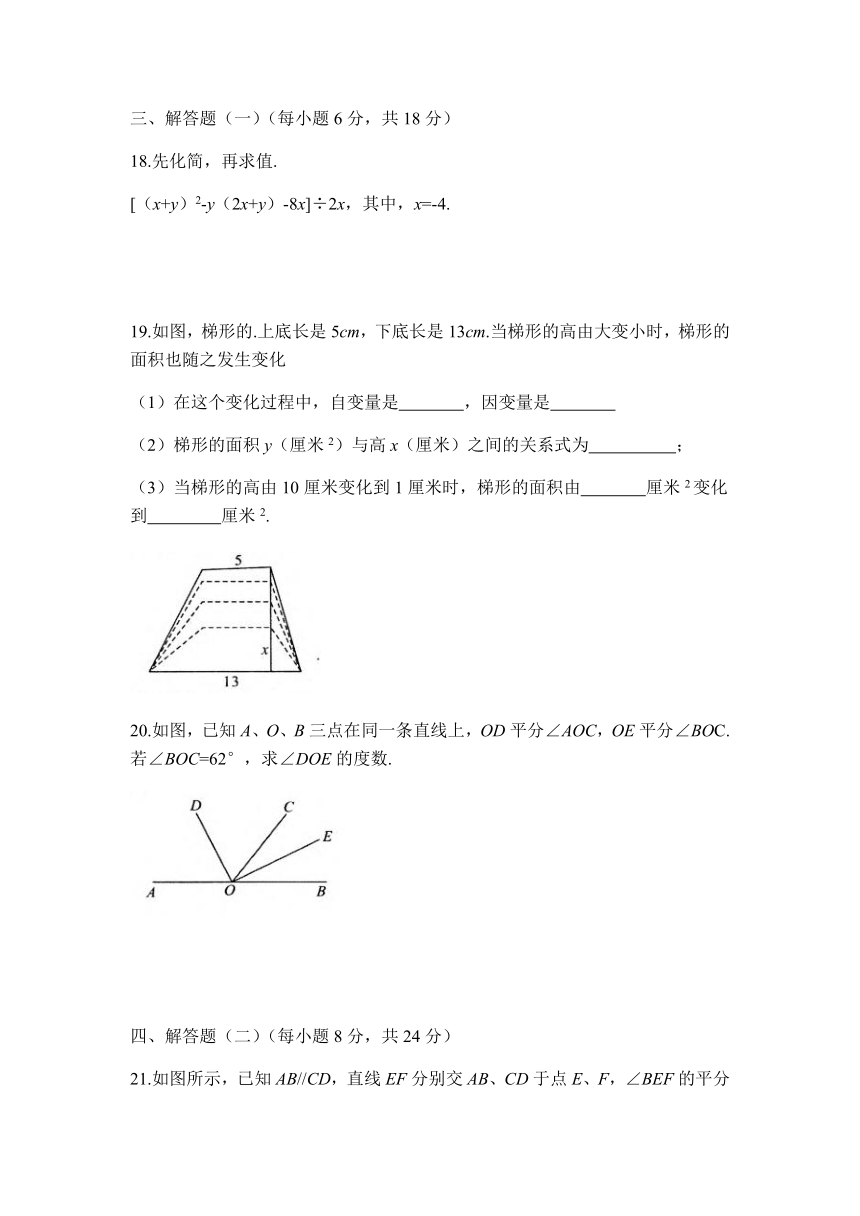
18.先化简,再求值.
[(x+y)2-y(2x+y)-8x]÷2x,其中,x=-4.
19.如图,梯形的.上底长是5cm,下底长是13cm.当梯形的高由大变小时,梯形的面积也随之发生变化
(1)在这个变化过程中,自变量是 ,因变量是
(2)梯形的面积y(厘米2)与高x(厘米)之间的关系式为 ;
(3)当梯形的高由10厘米变化到1厘米时,梯形的面积由 厘米2变化到 厘米2.
20.如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
四、解答题(二)(每小题8分,共24分)
21.如图所示,已知AB//CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EFP与∠FEP互余,试说明理由.
22.(1)已知3m=8,3n=2,求32m-3n+1的值;
(2)已知x2+x-1=0,求的值.
23.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN//BC交AB于M,交AC于N,若BM=2,CN=3,求线段MN的长.
五、解答题(三)(每小题10分,共20分)
24.如图是一个长方形花圃,花圃的一边靠墙,其他三边用12米长的篱笆围成.
(1)如果设花圃靠墙的一边长为x(米),花圃的面积y是多少平方米?
(2)当x从4米变到6米时,面积y如何变化?
25.如图,在△ABC中,AB=AC=8,BC=12,点.D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为t(0(1)运动 秒时,CD=3AE;
(2)运动多少秒时,△ABD≌△DCE能成立?说明理由;
(3)若△ABD≌△DCE,∠BAC=a,则∠ADE= (用含a的式子表示).
2021年-2022年北师大数学七年级下数学七年级下学期期中测试卷.
1.C 2.B 3.B 4.B 5.A 6.D 7.C 8.A 9.B
10.A 11., 12.∠1=∠2(答案不唯一) 13.45°
14. 15.0 16.100° 17.1
18.解:原式=(x2+2xy+y2)-2xy-y2-8x)÷2x
=(x2-8x)÷2x
=x-4
当x=-4时,
原式=×(-4)-4=-6
19.解:(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为y=(5+13)x×=9x;
(3)当梯形的高是10cm时,y=9×10=90(cm2).
当梯形的高是1cm时,y=9×1=9(cm2),
故当梯形的高由10cm变化到1cm时,梯形的面积由90cm2变化到9cm2.
故答案为(1)梯形的高、梯形的面积;(2)y=9x;(3)90,9.
20.解:∠DOE=(∠BOC+∠COA)=[62°+(180°-62°)]=90°
21.解:∵∠FEP=∠BEF,∠EFP=∠DFE,
∴∠EFP+∠FEP=(∠DFE+∠BEF)
∵AB//CD
∴∠BEF+∠DFE=180°
∴∠EFP+∠FEP=×180°=90°
∴∠EFP与∠FEP互余.
22.解:(1)∵3m=83n=2
∴32m-3n+l=(3m)2÷(3n)3×3
=82÷23×3
=24
(2)∵x2+x-1=0
∴x≠0
∴x+1-=0
即x-=-1
∴(x-)2=1
x2-2+=1
∴x2+=3
23.解:∵MN//BC,
∴∠MEB=∠CBE,∠NEC=∠BCE,
∵在△ABC中,∠ABC和∠ACB的平分线交于点E,
∴∠MBE=∠EBC,∠NCE=∠BCE,
∴∠MEB=∠MBE,∠NEC=∠NCE,
∴ME=MB,NE=NC,
∴MN=ME+NE=BM+CN=5,
故线段MN的长为5.
24.解:(1)长方形ABCD的长AD=BC=xm,则矩形的宽AB=CD=
因此矩形的面积为
(2)当x=4时,y=16;当x=6时,y=18,所以x从4m变到6m时,面积由16m2变到18m2.
25.解:(1)由题可得,BD=CE=2t,
∴CD=12-2t,AE=8-2t,
∴当AE=DC时,8-2t=(12-2t)
解得t=3
故答案为3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12-2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°-∠CDE-∠ADB,
∠B=180°-∠BAD-∠ADB
∴∠ADE=∠B
又∵∠BAC=a,AB=AC
∴∠ADE=∠B=(180°-a)=90°-a
故答案为90°-a
(满分120分)
一、选择题(每小题3分,共30分)
1.下列计算结果正确的是( )
A.2a3+a3=3a6 B.(-a)2·a3=-a6 C.()-2=4 D.(-2)0=-1
2.下列各式中,不能用平方差公式计算的是( )
A.(-4x+3y)(4x+3y) B.(4x-3y)(3y-4x)
C.(-4x+3y)(-4x-3y) D.(4x+3y)(4x-3y)
3.下列计算中,正确的是( )
A.3a3·2a2=6a6 B.2x2·3x2=6x4
C.3x2·4x2=12x2 D.5a3·3a5=15a15
4.已知a+b=3,ab=2,则a2+b2+ab的值为( )
A.5 B.7 C.9 D.13
5.若am=12,an=3,则am-n=( )
A.4 B.9 C.15 D.36
6.如图所示,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论不正确的是( )
A.∠2=45° B.∠1=∠3
C.∠AOD与∠1互为补角 D.∠1的余角等于75°30′
7.如图,AF是∠BAC的平分线,EF//AC交AB于点E,若∠1=25°,则∠BAF的度数为( )
A.15° B.50° C.25° D.12.5°
8.一条公路两次转弯后又回到原来的方向(即AB//CD),如图所示,如果第一次转弯时∠B=140°,那么∠C应等于( )
A.140° B.40° C.100° D.180°
9.关于圆的周长公式C=2πR,下列说法正确的是( )
A.π,R是自变量,2是常量
B.C是因变量,R是自变量,2,π是常量
C.R是自变量,2,π,C是常量
D.C是自变量,R是因变量,2,π是常量
10.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
二、填空题(每小题4分,共28分)
11.计算(-p)2·(-p)3= ;(a2b)3=
12.如图,请你写出一个能判定的条件
13.已知∠a的余角的3倍等于它的补角,则∠a=
14.如果多项式x2+mx+9是一个完全平方式,则m=
15.已知a,b,c是一个三角形的三条边长,则化简|a-b+c|-|b-a-c|的结果是
16.如图,∠1=120°,∠2=60°,∠3=100°,则∠4= 时,AB//EF.
17.如图,△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,点P在线段BC上以3cm/s的速度由点B向点C移动,同时,点Q在线段CA.上由点C向点A移动.若点Q的移动速度与点P的移动速度相同,则经过 秒后,△BPD≌△CQP.
三、解答题(一)(每小题6分,共18分)
18.先化简,再求值.
[(x+y)2-y(2x+y)-8x]÷2x,其中,x=-4.
19.如图,梯形的.上底长是5cm,下底长是13cm.当梯形的高由大变小时,梯形的面积也随之发生变化
(1)在这个变化过程中,自变量是 ,因变量是
(2)梯形的面积y(厘米2)与高x(厘米)之间的关系式为 ;
(3)当梯形的高由10厘米变化到1厘米时,梯形的面积由 厘米2变化到 厘米2.
20.如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
四、解答题(二)(每小题8分,共24分)
21.如图所示,已知AB//CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DFE的平分线相交于点P,则∠EFP与∠FEP互余,试说明理由.
22.(1)已知3m=8,3n=2,求32m-3n+1的值;
(2)已知x2+x-1=0,求的值.
23.如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN//BC交AB于M,交AC于N,若BM=2,CN=3,求线段MN的长.
五、解答题(三)(每小题10分,共20分)
24.如图是一个长方形花圃,花圃的一边靠墙,其他三边用12米长的篱笆围成.
(1)如果设花圃靠墙的一边长为x(米),花圃的面积y是多少平方米?
(2)当x从4米变到6米时,面积y如何变化?
25.如图,在△ABC中,AB=AC=8,BC=12,点.D从B出发以每秒2个单位的速度在线段BC上从点B向点C运动,点E同时从点C出发,以每秒2个单位的速度在线段AC上从点A运动,连接AD、DE,设D、E两点运动时间为t(0
(2)运动多少秒时,△ABD≌△DCE能成立?说明理由;
(3)若△ABD≌△DCE,∠BAC=a,则∠ADE= (用含a的式子表示).
2021年-2022年北师大数学七年级下数学七年级下学期期中测试卷.
1.C 2.B 3.B 4.B 5.A 6.D 7.C 8.A 9.B
10.A 11., 12.∠1=∠2(答案不唯一) 13.45°
14. 15.0 16.100° 17.1
18.解:原式=(x2+2xy+y2)-2xy-y2-8x)÷2x
=(x2-8x)÷2x
=x-4
当x=-4时,
原式=×(-4)-4=-6
19.解:(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm2)与高x(cm)之间的关系式为y=(5+13)x×=9x;
(3)当梯形的高是10cm时,y=9×10=90(cm2).
当梯形的高是1cm时,y=9×1=9(cm2),
故当梯形的高由10cm变化到1cm时,梯形的面积由90cm2变化到9cm2.
故答案为(1)梯形的高、梯形的面积;(2)y=9x;(3)90,9.
20.解:∠DOE=(∠BOC+∠COA)=[62°+(180°-62°)]=90°
21.解:∵∠FEP=∠BEF,∠EFP=∠DFE,
∴∠EFP+∠FEP=(∠DFE+∠BEF)
∵AB//CD
∴∠BEF+∠DFE=180°
∴∠EFP+∠FEP=×180°=90°
∴∠EFP与∠FEP互余.
22.解:(1)∵3m=83n=2
∴32m-3n+l=(3m)2÷(3n)3×3
=82÷23×3
=24
(2)∵x2+x-1=0
∴x≠0
∴x+1-=0
即x-=-1
∴(x-)2=1
x2-2+=1
∴x2+=3
23.解:∵MN//BC,
∴∠MEB=∠CBE,∠NEC=∠BCE,
∵在△ABC中,∠ABC和∠ACB的平分线交于点E,
∴∠MBE=∠EBC,∠NCE=∠BCE,
∴∠MEB=∠MBE,∠NEC=∠NCE,
∴ME=MB,NE=NC,
∴MN=ME+NE=BM+CN=5,
故线段MN的长为5.
24.解:(1)长方形ABCD的长AD=BC=xm,则矩形的宽AB=CD=
因此矩形的面积为
(2)当x=4时,y=16;当x=6时,y=18,所以x从4m变到6m时,面积由16m2变到18m2.
25.解:(1)由题可得,BD=CE=2t,
∴CD=12-2t,AE=8-2t,
∴当AE=DC时,8-2t=(12-2t)
解得t=3
故答案为3;
(2)当△ABD≌△DCE成立时,AB=CD=8,
∴12-2t=8,
解得t=2,
∴运动2秒时,△ABD≌△DCE能成立;
(3)当△ABD≌△DCE时,∠CDE=∠BAD,
又∵∠ADE=180°-∠CDE-∠ADB,
∠B=180°-∠BAD-∠ADB
∴∠ADE=∠B
又∵∠BAC=a,AB=AC
∴∠ADE=∠B=(180°-a)=90°-a
故答案为90°-a
同课章节目录
