人教版四年级下册数学第三单元运算定律——乘法运算律课件(共40张PPT)
文档属性
| 名称 | 人教版四年级下册数学第三单元运算定律——乘法运算律课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-28 00:00:00 | ||
图片预览






文档简介
(共40张PPT)
运算定律一
四年级下册
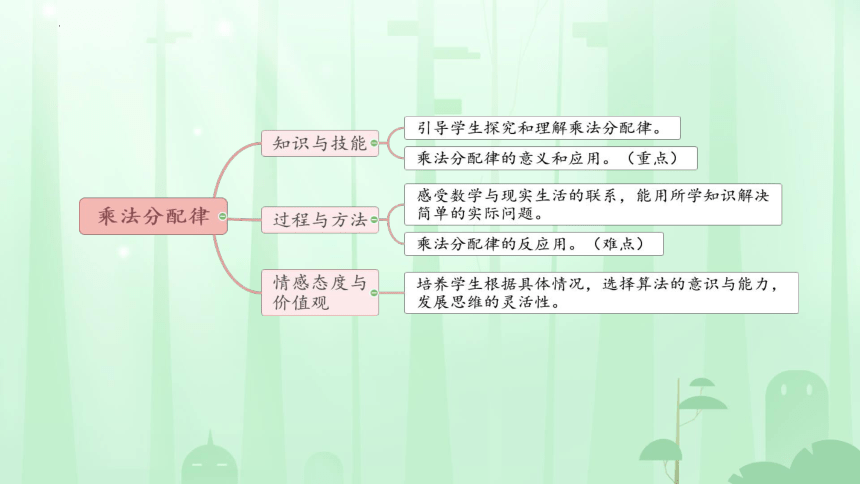
乘法分配律
知识点一
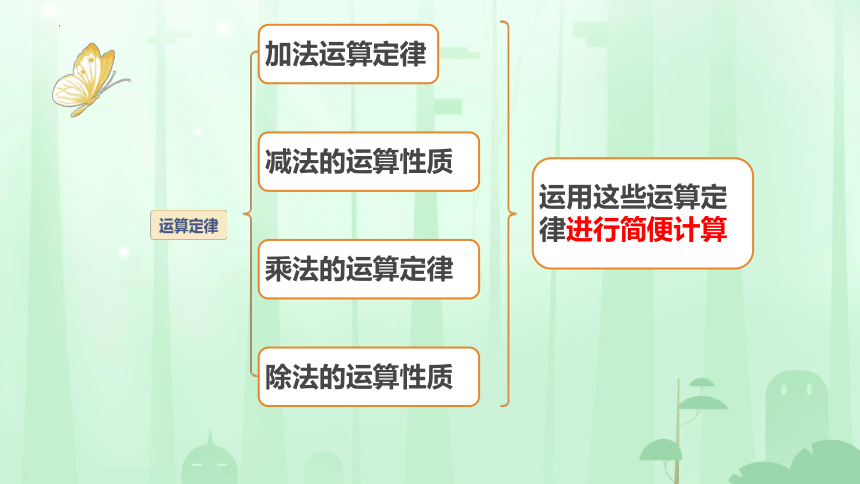
加法运算定律
减法的运算性质
乘法的运算定律
除法的运算性质
运用这些运算定律进行简便计算
巩固复习1:
1.加法运算有哪些运算定律?
加法交换律
加法结合律
2.用字母怎么表示?
加法运算定律
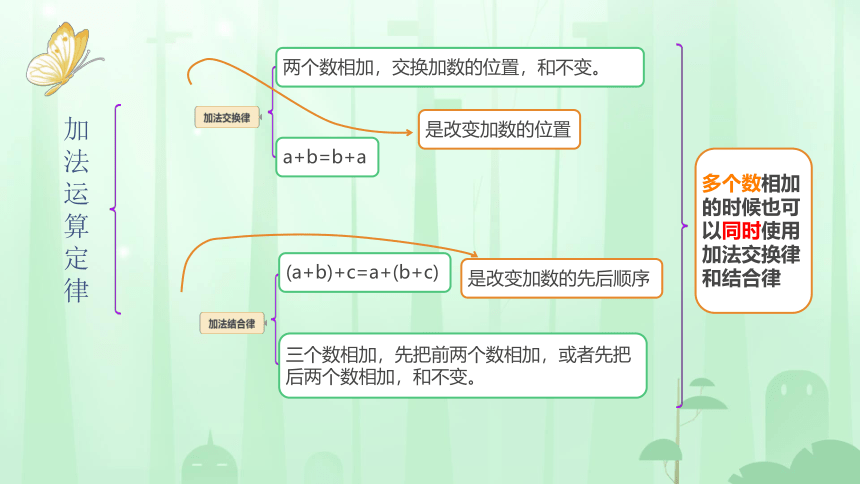
两个数相加,交换加数的位置,和不变。
a+b=b+a
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
是改变加数的位置
是改变加数的先后顺序
多个数相加的时候也可以同时使用加法交换律和结合律
减法的运算性质
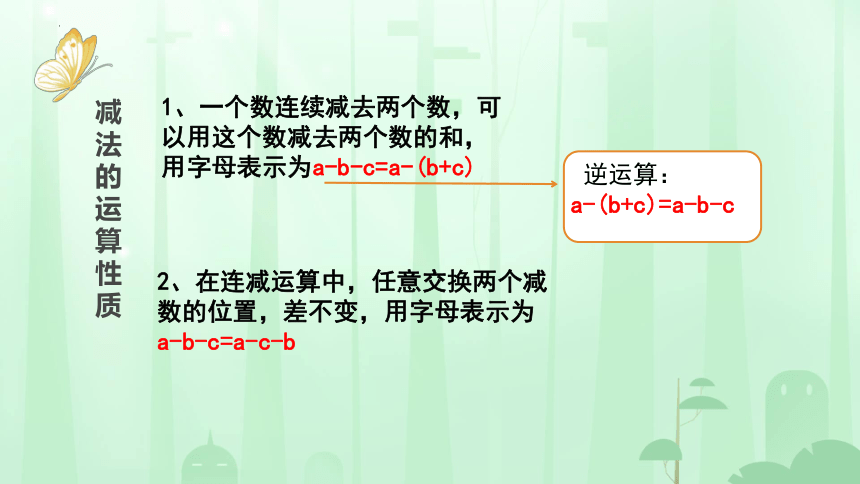
1、一个数连续减去两个数,可 以用这个数减去两个数的和, 用字母表示为a-b-c=a-(b+c)
2、在连减运算中,任意交换两个减 数的位置,差不变,用字母表示为 a-b-c=a-c-b
逆运算:
a-(b+c)=a-b-c
除法的运算性质
一个数连续除以两个数,可以用这个数除以两个数的积。
用字母表示为a÷b÷c=a÷(bⅹc)
除法运算性质的逆运算:a÷(bⅹc)=a÷b÷c
巩固复习2:
1.乘法运算有哪些运算定律?
乘法交换律
乘法结合律
2.用字母怎么表示?
乘法分配律
乘法的运算定律
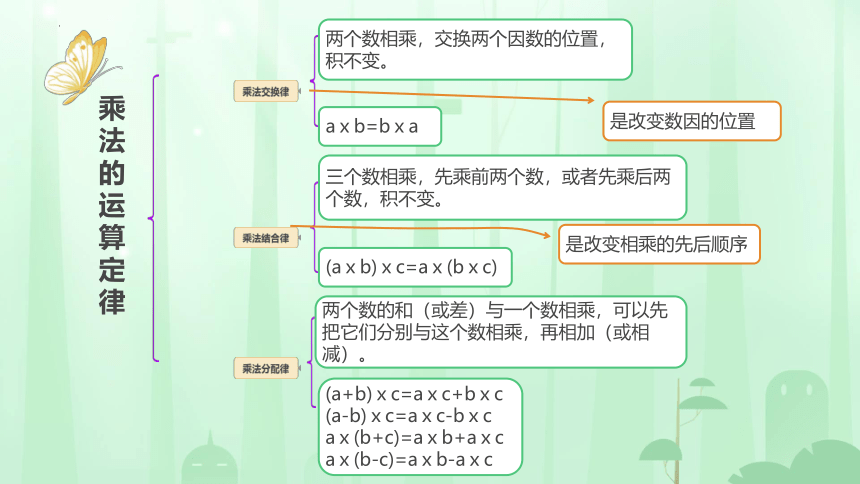
两个数相乘,交换两个因数的位置,积不变。
aⅹb=bⅹa
三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
(aⅹb)ⅹc=aⅹ(bⅹc)
两个数的和(或差)与一个数相乘,可以先把它们分别与这个数相乘,再相加(或相减)。
(a+b)ⅹc=aⅹc+bⅹc
(a-b)ⅹc=aⅹc-bⅹc
aⅹ(b+c)=aⅹb+aⅹc
aⅹ(b-c)=aⅹb-aⅹc
是改变数因的位置
是改变相乘的先后顺序
下列等式应用了什么运算定律。
(126+48)+52=126+(48+52) ( )
60×a=a×0 ( )
(3×25)×4=3×(25×4) ( )
加法结合律
乘法交换律
乘法结合律
复习导入
计算下面各题,怎样简便就怎样计算。
86+49+351
=86+(49+351)
=86+400
=486
143+64+57+136
=(143+57)+(64+136)
=200+200
=400
132-68-32
=132-(68+32)
=132-100
=32
76+237+24
=(76+24)+237
=100+237
=337
72ⅹ125
=9ⅹ(8ⅹ125)
=9ⅹ1000
=9000
4600÷25÷4
=4600÷(25ⅹ4)
=4600÷100
=46
计算题。
1、口算
125ⅹ8= 480÷8÷4= 50ⅹ19ⅹ2=
135+65= 360÷9ⅹ4= 732-74-26=
1000
200
12
160
1900
632
2、先计算,再用交换律进行验算。
1365+407= 86ⅹ15=
1 3 6 5
+ 4 0 7
1
1 7 7 2
验算:
4 0 7
+1 3 6 5
1
1 7 7 2
1772
8 6
ⅹ 1 5
3
4 3 0
8 6
1
1 2 9 0
验算:
1 5
ⅹ 8 6
3
9 0
1 2 0
4
1 2 9 0
1290
口算。
25×4= 125×8=
25×4×2= 125×8×2=
25×4×3= 125×8×3=
100
2000
1000
300
200
3000
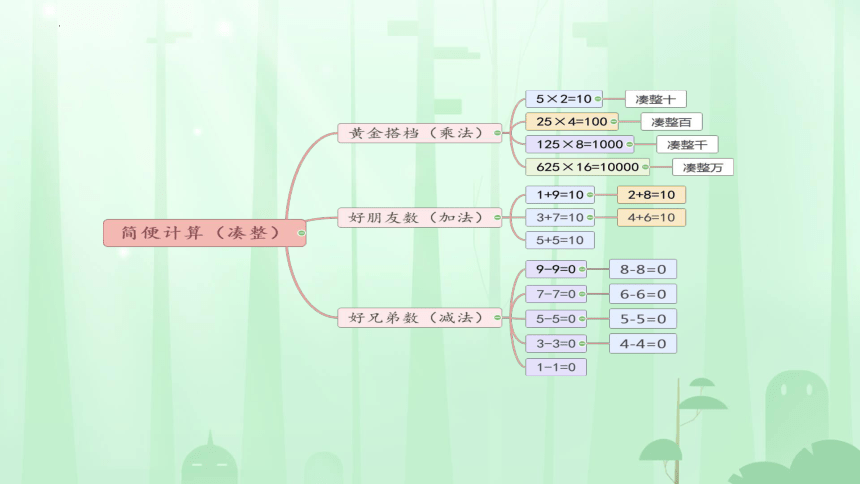
像25、4、2、8和125等这些数字相乘能凑成整百和整千数等,可使计算简便。
复习导入
说一说:我们已经学过哪些运算定律,并用字母表示。
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:a×(a+b)=a×b+a×c)
a×(a-b)=a×b-a×c)
说一说:仔细观察对比两个算式,你发现了什么规律?
(40+4)×25
=44×25
=1100
40×25+4×25
=1000+100
=1100
(40+4)×25=40×25+4×25
发现:(40+4)×25=40×25+4×25,
25×(40+4)=25×40+25×4,
两个数的和与其中一个数相乘,可以先把它们与这个数分别相乘,再相加。
先求出两个数的和,再乘第三个数。
先分别求出两个数的积,再相加。
(40+4)个25
40个25+4个25
?
结果相等
新课导入
举例验证你发现的规律。
(2)结论:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
(1)举例验证。
(40+2)×25=1050
40×25+2×25=1050
(40+2)×25=40×25+2×25
有时根据需要乘法分配律也可以逆用,用字母表示为a×b+a×c=a×(b+c)
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。
用字母表示为:(a+b)×c=a×c+b×c
小组讨论:可以用怎样的方式来表示乘法分配律 写写试试,并展示你的答案。
40×25+4×25
=
(40+4)×25
25×40+25×4
=
25×(40+4)
或:a×(b+c)=a×b+a×c
想一想:
方法二
方法一
方法三
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
6 0
1 2
2 5
×
2 4
3 0 0
12×25=
300
说一说:这3种不同的解法,你喜欢哪种?为什么
后两种方法都是根据数字的特点,利用运算定律使计算变得简便。
5 0
2 5
1 2
×
2 5 0
3 0 0
25×12
=25×(10+2)
=25×2+25×10
=50+250
=300
观察下边的竖式,说一说在计算的过程中运用了什么运算定律。
运用了乘法分配律
知识拓展
两个数的差与其中一个数相乘,可以用被减数和减数分别与这个数相乘,再相减。
用字母表示为(a-b)×c=a×c-b×c
或(b-c)×a=a×b-a×c
乘法结合律:(a×b)×c=a×(b×c)
想一想:怎样区分乘法结合律和乘法分配律呢?
乘法分配律:(a+b)×c=a×c+b×c
或a×(b+c)=a×b+a×c
(a-b)×c=a×c-b×c
或a×(b-c)=a×b-a×c
乘法结合律是三个数相乘的积,而乘法分配律是两个数的和或差,与另一个数相乘。
小结
归纳总结:乘法分配律
两个数的和或差与一个数相乘,可以先把它们与这个数分别相乘,再相加或相减。这叫作乘法分配律。
用字母表示为(a+b)×c=a×c+b×c,
也可以表示为a×(b+c)=a×b+a×c;
知识拓展:
(a-b)×c=a×c-b×c,
(b-c)×a=b×a-c×a。
56×(19+28)=56×19+28 ( )
32×(7×3)=32×7+32×3 ( )
下面哪些算式是正确的?正确的画“√”,错误的画“×”。
64×64+36×64=(64+36)×64 ( )
28×56
乘法分配律含有“+”和“×”
课堂练习
35×5×20 25×(4+8) 2000÷125÷8
=35×(5×20)
=35×100
=3500
=25×4+25×8
=100+200
=300
计算下面各题,怎么简便就怎样算。
=2000÷(125×8)
=2000÷1000
=2
课堂练习
知识拓展
5cm
8cm
3cm
用组合图形的面积也可以表示乘法对加法的分配律。
下面哪些算式运用了乘法分配律?
117×3+117×7=117×(3+7)
24×(5+12)=24×17
4×a+a×5=(4+5)×a
36×(4×6)=36×6×4
(34+125)×8
连一连。
18×16+18×38
7×a+4×a
125×(57+23)
18×(16+38)
(7-4)×a
125×23+57×125
34×8+125×8
李大爷有一块菜地(如下图),这块菜地的面积有多少平方米?
乘99类型
知识点二
43ⅹ98 101ⅹ38-38
=43ⅹ(100-2)
=43ⅹ100-43ⅹ2
=4300-86
=4214
=(100-1)ⅹ38
=100ⅹ38
=3800
=38ⅹ1
计算下面各题,怎样简便就怎样计算。
(1)99×23
(2)102×23
课堂小结
这节课你们都学会了哪些知识?
课后作业
自我巩固:1~10题、例题、笔记
(建议:一天做3-5个题、周四之前网上提交自我巩固、钉钉群里发笔记)
作业:计算下面各题,怎样简便就怎样计算。
81ⅹ4ⅹ25 947-347-253 48ⅹ101-48
99ⅹ26 28ⅹ15+28ⅹ4+28 252+135+48+165
101ⅹ93 435ⅹ25-35ⅹ25 52ⅹ97 72ⅹ103
培优练习:巧算
99999×7+22222
、
77777×9+4444
8888×11
10001×10
1001×100
通过今天的复习,我相信在以后做题的过程中你会很熟练地运用运算定律进行解答的!
再 见!
下周再见啦
运算定律一
四年级下册
乘法分配律
知识点一
加法运算定律
减法的运算性质
乘法的运算定律
除法的运算性质
运用这些运算定律进行简便计算
巩固复习1:
1.加法运算有哪些运算定律?
加法交换律
加法结合律
2.用字母怎么表示?
加法运算定律
两个数相加,交换加数的位置,和不变。
a+b=b+a
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
(a+b)+c=a+(b+c)
是改变加数的位置
是改变加数的先后顺序
多个数相加的时候也可以同时使用加法交换律和结合律
减法的运算性质
1、一个数连续减去两个数,可 以用这个数减去两个数的和, 用字母表示为a-b-c=a-(b+c)
2、在连减运算中,任意交换两个减 数的位置,差不变,用字母表示为 a-b-c=a-c-b
逆运算:
a-(b+c)=a-b-c
除法的运算性质
一个数连续除以两个数,可以用这个数除以两个数的积。
用字母表示为a÷b÷c=a÷(bⅹc)
除法运算性质的逆运算:a÷(bⅹc)=a÷b÷c
巩固复习2:
1.乘法运算有哪些运算定律?
乘法交换律
乘法结合律
2.用字母怎么表示?
乘法分配律
乘法的运算定律
两个数相乘,交换两个因数的位置,积不变。
aⅹb=bⅹa
三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
(aⅹb)ⅹc=aⅹ(bⅹc)
两个数的和(或差)与一个数相乘,可以先把它们分别与这个数相乘,再相加(或相减)。
(a+b)ⅹc=aⅹc+bⅹc
(a-b)ⅹc=aⅹc-bⅹc
aⅹ(b+c)=aⅹb+aⅹc
aⅹ(b-c)=aⅹb-aⅹc
是改变数因的位置
是改变相乘的先后顺序
下列等式应用了什么运算定律。
(126+48)+52=126+(48+52) ( )
60×a=a×0 ( )
(3×25)×4=3×(25×4) ( )
加法结合律
乘法交换律
乘法结合律
复习导入
计算下面各题,怎样简便就怎样计算。
86+49+351
=86+(49+351)
=86+400
=486
143+64+57+136
=(143+57)+(64+136)
=200+200
=400
132-68-32
=132-(68+32)
=132-100
=32
76+237+24
=(76+24)+237
=100+237
=337
72ⅹ125
=9ⅹ(8ⅹ125)
=9ⅹ1000
=9000
4600÷25÷4
=4600÷(25ⅹ4)
=4600÷100
=46
计算题。
1、口算
125ⅹ8= 480÷8÷4= 50ⅹ19ⅹ2=
135+65= 360÷9ⅹ4= 732-74-26=
1000
200
12
160
1900
632
2、先计算,再用交换律进行验算。
1365+407= 86ⅹ15=
1 3 6 5
+ 4 0 7
1
1 7 7 2
验算:
4 0 7
+1 3 6 5
1
1 7 7 2
1772
8 6
ⅹ 1 5
3
4 3 0
8 6
1
1 2 9 0
验算:
1 5
ⅹ 8 6
3
9 0
1 2 0
4
1 2 9 0
1290
口算。
25×4= 125×8=
25×4×2= 125×8×2=
25×4×3= 125×8×3=
100
2000
1000
300
200
3000
像25、4、2、8和125等这些数字相乘能凑成整百和整千数等,可使计算简便。
复习导入
说一说:我们已经学过哪些运算定律,并用字母表示。
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:a×(a+b)=a×b+a×c)
a×(a-b)=a×b-a×c)
说一说:仔细观察对比两个算式,你发现了什么规律?
(40+4)×25
=44×25
=1100
40×25+4×25
=1000+100
=1100
(40+4)×25=40×25+4×25
发现:(40+4)×25=40×25+4×25,
25×(40+4)=25×40+25×4,
两个数的和与其中一个数相乘,可以先把它们与这个数分别相乘,再相加。
先求出两个数的和,再乘第三个数。
先分别求出两个数的积,再相加。
(40+4)个25
40个25+4个25
?
结果相等
新课导入
举例验证你发现的规律。
(2)结论:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
(1)举例验证。
(40+2)×25=1050
40×25+2×25=1050
(40+2)×25=40×25+2×25
有时根据需要乘法分配律也可以逆用,用字母表示为a×b+a×c=a×(b+c)
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。
用字母表示为:(a+b)×c=a×c+b×c
小组讨论:可以用怎样的方式来表示乘法分配律 写写试试,并展示你的答案。
40×25+4×25
=
(40+4)×25
25×40+25×4
=
25×(40+4)
或:a×(b+c)=a×b+a×c
想一想:
方法二
方法一
方法三
12×25
=(3×4)×25
=3×(4×25)
=3×100
=300
12×25
=(10+2)×25
=10×25+2×25
=250+50
=300
6 0
1 2
2 5
×
2 4
3 0 0
12×25=
300
说一说:这3种不同的解法,你喜欢哪种?为什么
后两种方法都是根据数字的特点,利用运算定律使计算变得简便。
5 0
2 5
1 2
×
2 5 0
3 0 0
25×12
=25×(10+2)
=25×2+25×10
=50+250
=300
观察下边的竖式,说一说在计算的过程中运用了什么运算定律。
运用了乘法分配律
知识拓展
两个数的差与其中一个数相乘,可以用被减数和减数分别与这个数相乘,再相减。
用字母表示为(a-b)×c=a×c-b×c
或(b-c)×a=a×b-a×c
乘法结合律:(a×b)×c=a×(b×c)
想一想:怎样区分乘法结合律和乘法分配律呢?
乘法分配律:(a+b)×c=a×c+b×c
或a×(b+c)=a×b+a×c
(a-b)×c=a×c-b×c
或a×(b-c)=a×b-a×c
乘法结合律是三个数相乘的积,而乘法分配律是两个数的和或差,与另一个数相乘。
小结
归纳总结:乘法分配律
两个数的和或差与一个数相乘,可以先把它们与这个数分别相乘,再相加或相减。这叫作乘法分配律。
用字母表示为(a+b)×c=a×c+b×c,
也可以表示为a×(b+c)=a×b+a×c;
知识拓展:
(a-b)×c=a×c-b×c,
(b-c)×a=b×a-c×a。
56×(19+28)=56×19+28 ( )
32×(7×3)=32×7+32×3 ( )
下面哪些算式是正确的?正确的画“√”,错误的画“×”。
64×64+36×64=(64+36)×64 ( )
28×56
乘法分配律含有“+”和“×”
课堂练习
35×5×20 25×(4+8) 2000÷125÷8
=35×(5×20)
=35×100
=3500
=25×4+25×8
=100+200
=300
计算下面各题,怎么简便就怎样算。
=2000÷(125×8)
=2000÷1000
=2
课堂练习
知识拓展
5cm
8cm
3cm
用组合图形的面积也可以表示乘法对加法的分配律。
下面哪些算式运用了乘法分配律?
117×3+117×7=117×(3+7)
24×(5+12)=24×17
4×a+a×5=(4+5)×a
36×(4×6)=36×6×4
(34+125)×8
连一连。
18×16+18×38
7×a+4×a
125×(57+23)
18×(16+38)
(7-4)×a
125×23+57×125
34×8+125×8
李大爷有一块菜地(如下图),这块菜地的面积有多少平方米?
乘99类型
知识点二
43ⅹ98 101ⅹ38-38
=43ⅹ(100-2)
=43ⅹ100-43ⅹ2
=4300-86
=4214
=(100-1)ⅹ38
=100ⅹ38
=3800
=38ⅹ1
计算下面各题,怎样简便就怎样计算。
(1)99×23
(2)102×23
课堂小结
这节课你们都学会了哪些知识?
课后作业
自我巩固:1~10题、例题、笔记
(建议:一天做3-5个题、周四之前网上提交自我巩固、钉钉群里发笔记)
作业:计算下面各题,怎样简便就怎样计算。
81ⅹ4ⅹ25 947-347-253 48ⅹ101-48
99ⅹ26 28ⅹ15+28ⅹ4+28 252+135+48+165
101ⅹ93 435ⅹ25-35ⅹ25 52ⅹ97 72ⅹ103
培优练习:巧算
99999×7+22222
、
77777×9+4444
8888×11
10001×10
1001×100
通过今天的复习,我相信在以后做题的过程中你会很熟练地运用运算定律进行解答的!
再 见!
下周再见啦
