8.5.2直线与平面平行
图片预览
文档简介
中小学教育资源及组卷应用平台
8.5.2 直线与平面平行
班级 姓名
学习目标
1.掌握直线与平面平行的判定定理和性质定理,并能利用这两个定理解决空间中的平行关系问题.
2.利用直线与平面平行的判定定理和性质定理证明空间平行问题.
学习过程
自学指导 自学检测及课堂展示
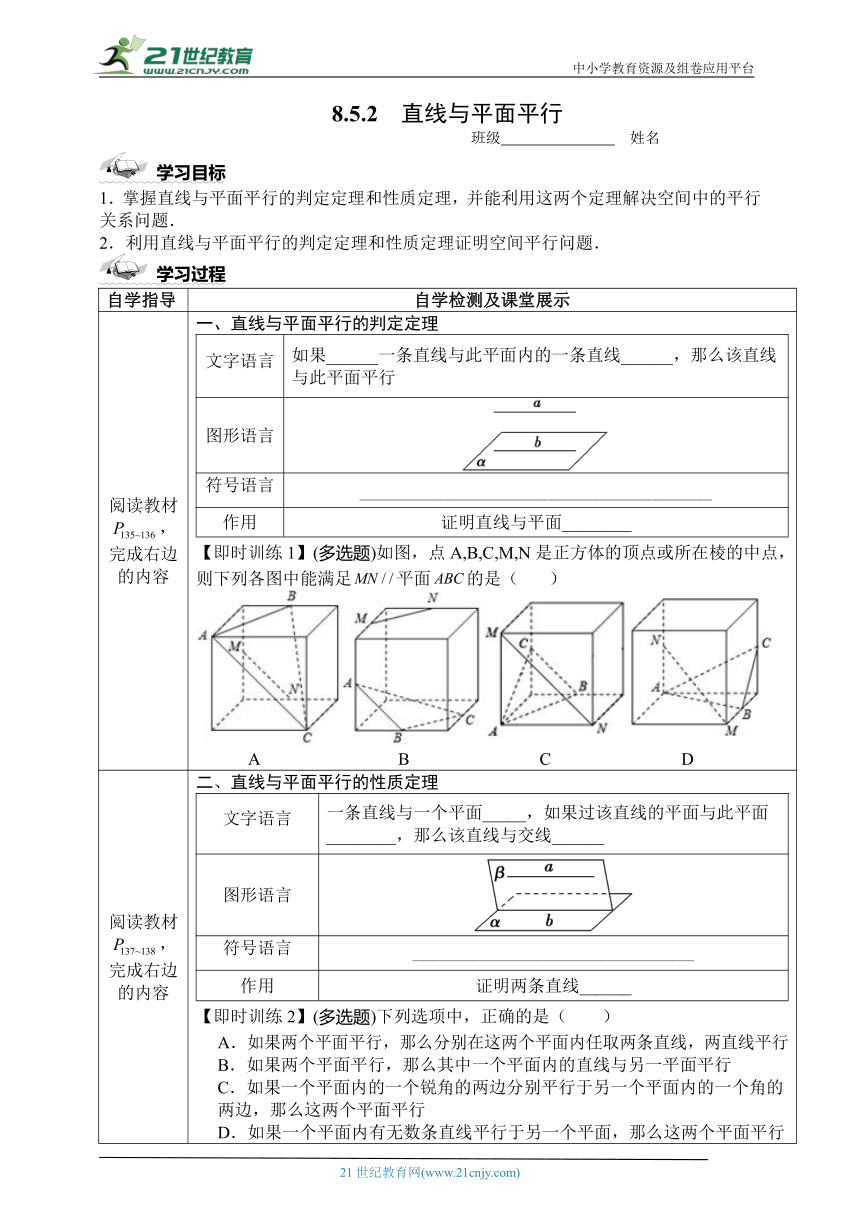
阅读教材,完成右边的内容 一、直线与平面平行的判定定理文字语言如果______一条直线与此平面内的一条直线______,那么该直线与此平面平行图形语言符号语言 _____________________________________________________________作用证明直线与平面________【即时训练1】(多选题)如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则下列各图中能满足平面的是( )A B C D
阅读教材,完成右边的内容 二、直线与平面平行的性质定理文字语言一条直线与一个平面_____,如果过该直线的平面与此平面________,那么该直线与交线______图形语言符号语言 ____________________________________________________作用证明两条直线______【即时训练2】(多选题)下列选项中,正确的是( )A.如果两个平面平行,那么分别在这两个平面内任取两条直线,两直线平行B.如果两个平面平行,那么其中一个平面内的直线与另一平面平行C.如果一个平面内的一个锐角的两边分别平行于另一个平面内的一个角的两边,那么这两个平面平行D.如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行
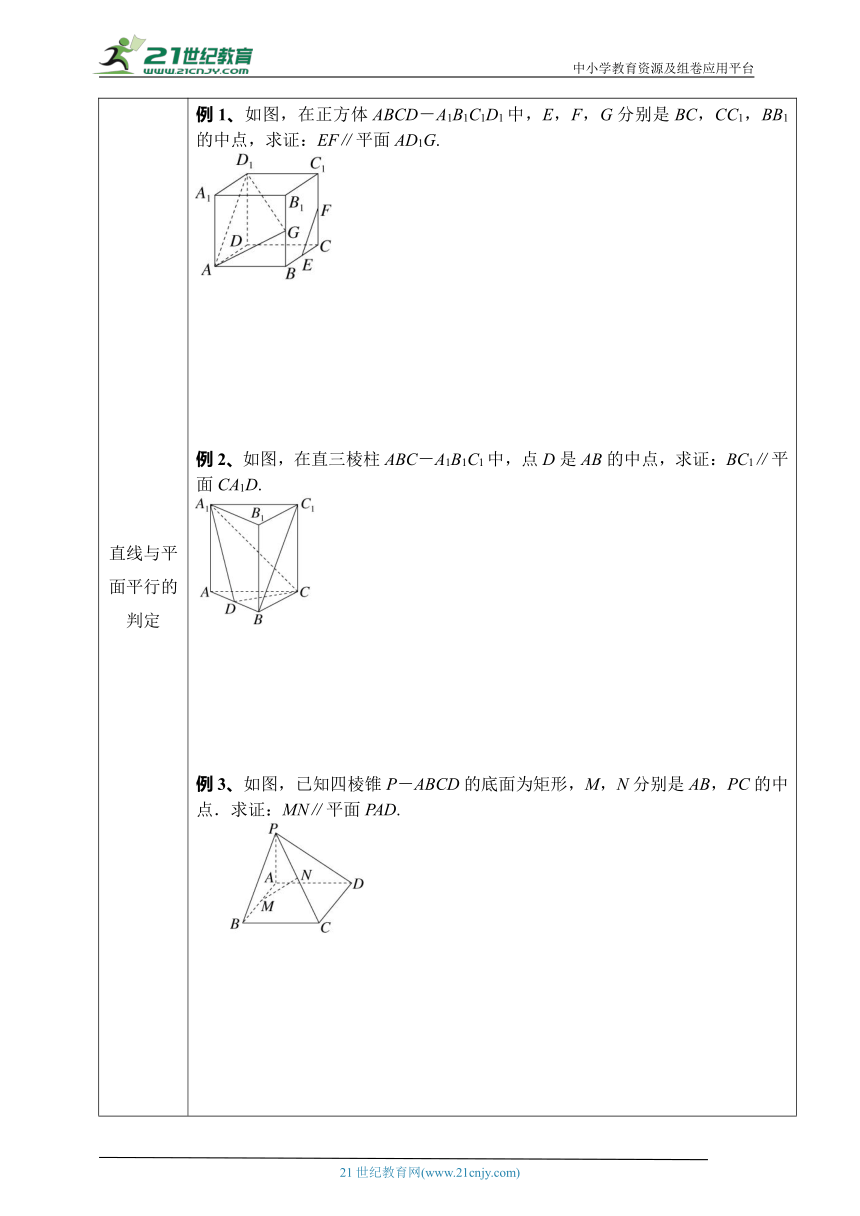
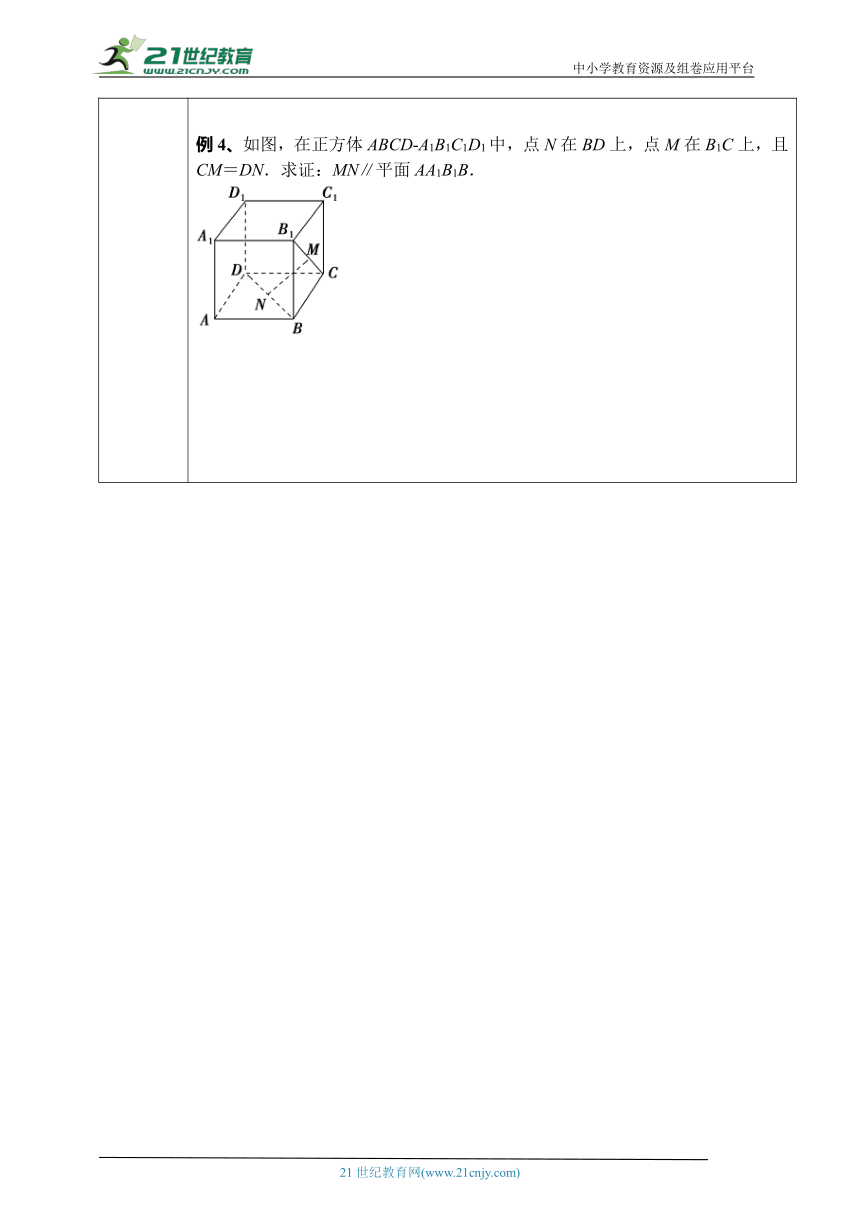
直线与平面平行的判定 例1、如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.例2、如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,求证:BC1∥平面CA1D.例3、如图,已知四棱锥P-ABCD的底面为矩形,M,N分别是AB,PC的中点.求证:MN∥平面PAD.例4、如图,在正方体ABCD A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥平面AA1B1B.
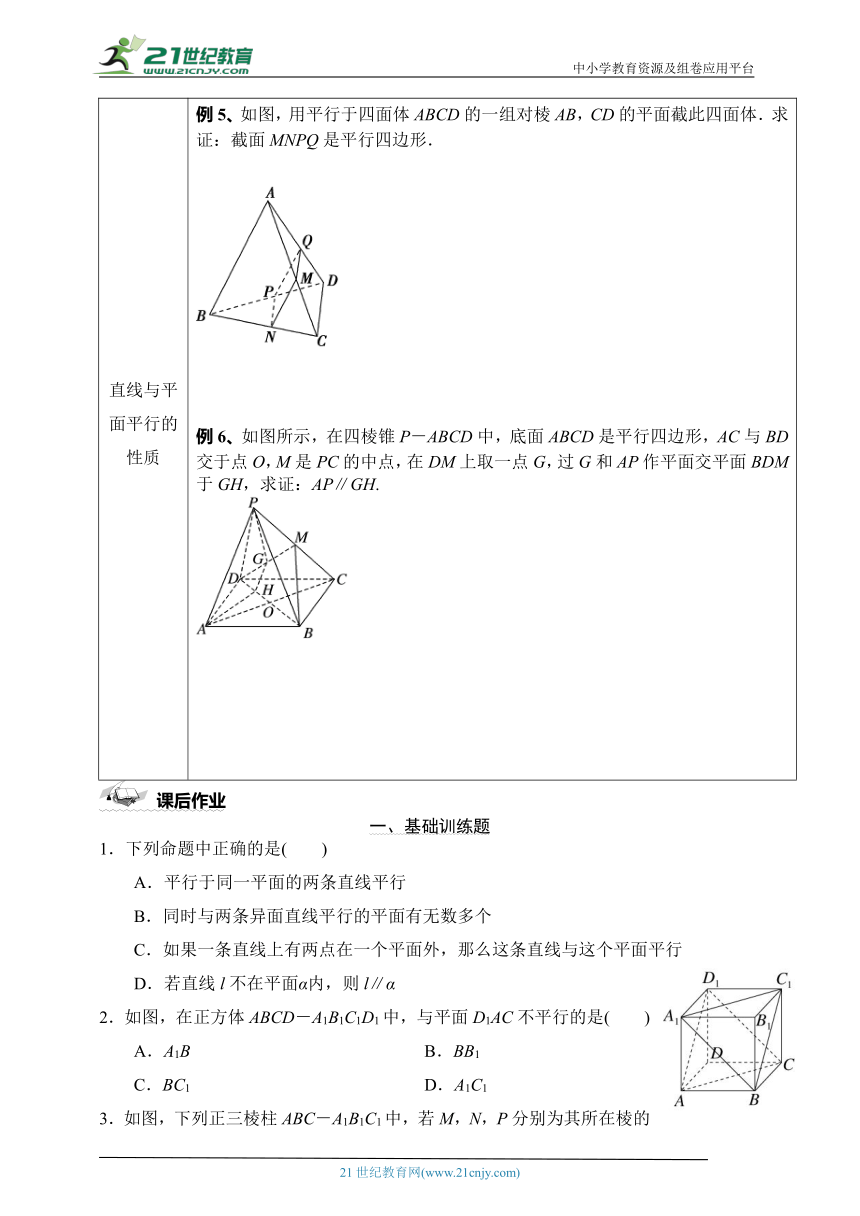
直线与平面平行的性质 例5、如图,用平行于四面体ABCD的一组对棱AB,CD的平面截此四面体.求证:截面MNPQ是平行四边形.例6、如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH. INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\数学 人A 必修第二册(新教材)最新(加双选)\\8-201.TIF" \* MERGEFORMATINET
课后作业
一、基础训练题
1.下列命题中正确的是( )
A.平行于同一平面的两条直线平行
B.同时与两条异面直线平行的平面有无数多个
C.如果一条直线上有两点在一个平面外,那么这条直线与这个平面平行
D.若直线l不在平面α内,则l∥α
2.如图,在正方体ABCD-A1B1C1D1中,与平面D1AC不平行的是( )
A.A1B B.BB1
C.BC1 D.A1C1
3.如图,下列正三棱柱ABC-A1B1C1中,若M,N,P分别为其所在棱的中点,则不能得出AB∥平面MNP的是( )
4.(多选题)若直线a平行于平面α,则下列结论正确的是( )
A.直线a与平面α无交点
B.直线a平行于平面α内的所有直线
C.平面α内有无数条直线与直线a平行
D.平面α内存在无数条直线与直线a为异面直线
5.在长方体ABCD A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有( )
A.2个 B.3个 C.4个 D.5个
6.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,H,G分别为BC,CD的中点,则( )
A.BD∥平面EFG,且四边形EFGH是平行四边形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是平行四边形
D.EH∥平面ADC,且四边形EFGH是梯形
7.(多选题)一几何体的平面展开图如下左图所示(顶点P在展开图中分别为P1,P2,P3,P4),其中四边形ABCD为正方形,E,F分别为P4B,P1C的中点,在此几何体中,给出的下列结论中正确的是( )
A.直线AE与直线BF异面 B.直线AE与直线DF异面
C.直线EF∥平面PAD D.直线EF∥平面ABCD
8.如上右图,直线a∥平面α,A是平面α的另一侧的点,点B,C,D∈a,线段AB,AC,AD分别交α于点E,F,G,若BD=4,CF=4,AF=5,则EG=( )
A. B.
C. D.
9.对于直线m,n和平面α,下面命题中的真命题是( )
A.如果m α,n α,m,n是异面直线,那么n∥α
B.如果m α,n与α相交,那么m,n是异面直线
C.如果m α,n∥α,m,n共面,那么m∥n
D.如果m∥α,n∥α,m,n共面,那么m∥n
10.如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出以下结论:
①OM∥PD;
②OM∥平面PCD;
③OM∥平面PDA;
④OM∥平面PBA;
⑤OM∥平面PBC.其中正确的个数是( )
A.1 B.2 C.3 D.4
11.如下左图,ABCD A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是________.
12.如上右图,P为 ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,=________.
13.如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.求证:AM∥平面BDE.
14.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE,若存在,指出点M的位置,并证明你的结论.
15.如图所示,在三棱柱ABC-A1B1C1中,D是棱CC1的中点,E是棱AB的中点,证明:DE∥平面AB1C1.
16.如图所示,四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.
(1)求证:AB∥平面EFGH,CD∥平面EFGH;
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
二、综合训练题
17.a,b是两条异面直线,下列结论正确的是( )
A.过不在a,b上的任一点,可作一个平面与a,b平行
B.过不在a,b上的任一点,可作一条直线与a,b相交
C.过不在a,b上的任一点,可作一条直线与a,b都平行
D.过a可以并且只可以作一个平面与b平行
18.如图,四棱锥S ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
19.(多选题)如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,下列说法正确的是( )
A.水的部分始终呈棱柱状
B.水面四边形EFGH的面积不改变
C.棱A1D1始终与水面EFGH平行
D.当E∈AA1时,AE+BF是定值
三、能力提升题
20.如图所示,ABCD A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
21.如图,已知E,F分别是菱形ABCD的边BC,CD的中点,EF与AC交于点O,点P在平面ABCD外,M是线段PA上一动点,若PC∥平面MEF,试确定点M的位置.
8.5.2 直线与平面平行
参考答案
例1、【证明】连接BC1(图略),在△BCC1中,
∵E,F分别为BC,CC1的中点,∴EF∥BC1,
又∵AB∥A1B1∥D1C1,且AB=A1B1=D1C1,
∴四边形ABC1D1是平行四边形,
∴BC1∥AD1,∴EF∥AD1,又EF 平面AD1G,
AD1 平面AD1G,∴EF∥平面AD1G.
例2、【证明】如图所示,连接AC1交A1C于点O,连接OD,则O是AC1的中点.
又∵点D是AB的中点,∴OD∥BC1.
又∵OD 平面CA1D,BC1 平面CA1D,
∴BC1∥平面CA1D.
例3、【证明】如图,取PD中点E,连接AE,NE.
∵N,E分别为PC,PD的中点,∴NECD.
又∵M为AB中点,底面ABCD为矩形,
∴AMCD,∴AMNE.
∴四边形AMNE为平行四边形,∴MN∥AE.
又∵MN 面PAD,AE 面PAD,
∴MN∥面PAD.
例4、【证明】法一:如图,作ME∥BC,交BB1于点E,作NF∥AD,
交AB于点F,连接EF,则EF 平面AA1B1B,
且=,=.
∵在正方体ABCD A1B1C1D1中,CM=DN,B1C=BD,∴B1M=NB.
∴==.又AD=BC,
∴ME=NF.又ME∥BC∥AD∥NF,
∴四边形MEFN为平行四边形.∴MN∥EF.
∵MN 平面AA1B1B,EF 平面AA1B1B,
∴MN∥平面AA1B1B.
法二:如图②,连接CN并延长交BA所在直线于点P,连接B1P,则B1P 平面AA1B1B.
∵△NDC∽△NBP,∴=.
又CM=DN,B1C=BD,
∴==.∴MN∥B1P.
∵MN 平面AA1B1B,B1P 平面AA1B1B,
∴MN∥平面AA1B1B.
例5、【证明】因为AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,且AB 平面ABC,
所以由线面平行的性质定理,知AB∥MN.
同理,AB∥PQ,
所以MN∥PQ.同理可得MQ∥NP.
所以截面MNPQ是平行四边形.
例6、【证明】连接MO.
∵四边形ABCD是平行四边形,
∴O是AC的中点.又∵M是PC的中点,∴AP∥OM.
又∵AP 平面BDM,OM 平面BDM,∴AP∥平面BDM.
又∵AP 平面APGH,平面APGH∩平面BDM=GH,∴AP∥GH.
课后作业
1、【答案】B
2、【答案】B
【解析】∵A1B∥D1C,且D1C 平面D1AC,A1B 平面D1AC,∴A1B∥平面D1AC.
∵BC1∥AD1,且AD1 平面D1AC,BC1 平面D1AC,∴BC1∥平面D1AC.
∵A1C1∥AC,且AC 平面D1AC,A1C1 平面D1AC,∴A1C1∥平面D1AC.
3、【答案】C
【解析】在A、B中,易知AB∥A1B1∥MN,由线面平行的判定定理得AB∥平面MNP;在D中,易知AB∥PN,由线面平行的判定定理得AB∥平面MNP.在C中,易知A1B1与平面MNP相交,由AB∥A1B1知AB与平面MNP相交,故选C.
4、【答案】ACD
【解析】由题意知,直线a平行于平面α.直线a与平面α无交点,A正确;直线a与平面α内的直线可能平行或异面,B不正确;平面α内有无数条直线与直线a平行,C正确;平面α内存在无数条直线与直线a成异面直线,D正确.故选ACD.
5、【答案】B
【解析】如图所示,结合图形可知AA1∥平面BC1,AA1∥平面DC1,AA1∥平面BB1D1D.
6、【答案】B
【解析】如图,由题意,得EF∥BD,且EF=BD,HG∥BD,且HG=BD,∴EF∥HG且EF≠HG,∴四边形EFGH是梯形.又EF∥BD,EF 平面BCD,BD 平面BCD,
∴EF∥平面BCD,分析知EH与平面ADC不平行.故选B.
7、【答案】ACD
【解析】如图,将平面展开图还原为几何体,显然AE,BF异面,可知A正确;
易得EF∥BC,又BC∥AD,∴EF∥AD,又EF 平面PAD,AD 平面PAD,
∴EF∥平面PAD,可知C正确;
易知四边形AEFD为梯形,可知B错误;∵EF∥BC,BC 平面ABCD,EF 平面ABCD,
∴EF∥平面ABCD,故D正确.故选ACD.
8、【答案】B
【解析】∵a∥α,α∩平面ABD=EG,a 平面ABD,∴a∥EG,即BD∥EG,
∴==,则EG===.故选B.
9、【答案】C
【解析】对于A,如果m α,n α,m,n是异面直线,则n∥α或n与α相交,故A错;对于B,如果m α,n与α相交,则m,n相交或是异面直线,故B错;对于C,如果m α,n∥α,m,n共面,由线面平行的性质定理,可得m∥n,故C对;对于D,如果m∥α,n∥α,m,n共面,则m∥n或m,n相交,故D错.
10、【答案】C
【解析】由题意知,OM∥PD,PD 平面PCD,PD 平面PDA,OM 平面PCD,OM 平面PDA,所以OM∥平面PCD,OM∥平面PDA.故选C.
11、【答案】平行
【解析】连接A1C1(图略),∵AC∥A1C1,∴AC∥平面A1B1C1D1,
又∵AC 平面AB1C,平面AB1C∩平面A1B1C1D1=l,∴AC∥l.
12、【答案】
【解析】连接AC交BE于G,连接FG,因为PA∥平面EBF,
PA 平面PAC,平面PAC∩平面BEF=FG,所以PA∥FG,所以=.
又因为AD∥BC,E为AD的中点,所以==,所以=.
13、【证明】如图,记AC与BD的交点为O,连接OE.
∵O,M分别是AC,EF的中点,四边形ACEF是矩形,
∴EM∥OA,且EM=OA,
∴四边形AOEM是平行四边形,∴AM∥OE.
又OE 平面BDE,AM 平面BDE,
∴AM∥平面BDE.
14、[解] 存在点M,如图,当点M是线段AE的中点时,PM∥平面BCE.
证明如下:取BE的中点N,连接CN,MN,则MN∥AB且MN=AB.
又PC∥AB且PC=AB,所以MN∥PC且MN=PC,
所以四边形MNCP为平行四边形,所以PM∥CN.
因为PM 平面BCE,CN 平面BCE,
所以PM∥平面BCE.
15、【证明】如图,取AB1的中点H,连接EH,HC1.∵E是棱AB的中点,∴EH∥BB1,且EH=BB1.
∵D是棱CC1的中点,∴DC1=CC1,
又BB1∥CC1,且BB1=CC1,∴DC1∥BB1,且DC1=BB1,
∴EH∥DC1,且EH=DC1,
∴四边形EHC1D为平行四边形,∴DE∥HC1.
又∵HC1 平面AB1C1,DE 平面AB1C1,
∴DE∥平面AB1C1.
16、[解析] (1)证明:∵四边形EFGH为平行四边形,∴EF∥HG.
∵HG 平面ABD,EF 平面ABD,∴EF∥平面ABD.∵EF 平面ABC,
平面ABD∩平面ABC=AB,∴EF∥AB.
又EF 平面EFGH,AB 平面EFGH.∴AB∥平面EFGH.同理可证CD∥平面EFGH.
(2)设EF=x(0从而FG=6-x.∴四边形EFGH的周长l=2=12-x.
又017、【答案】D
【解析】A错,若点与a所确定的平面与b平行时,就不能使这个平面与a平行了.
B错,若点与a所确定的平面与b平行时,就不能作一条直线与a,b相交.
C错,假如这样的直线存在,根据基本事实4就可有a∥b,这与a,b异面矛盾.
D正确,在a上任取一点A,过A点做直线c∥b,则c与a确定一个平面与b平行,这个平面是唯一的.
18、【答案】C
【解析】由AB=BC=CD=DA=2,得AB∥CD,即AB∥平面DCFE,
∵平面SAB∩平面DCFE=EF,∴AB∥EF.∵E是SA的中点,
∴EF=1,DE=CF=.∴四边形DEFC的周长为3+2.
19、【答案】ACD
【解析】将该四棱柱绕BC旋转,面ABFE与面DCGH始终平行且全等,其余面为四边形,且相邻棱平行,所以ABFE-DCGH始终呈棱柱状,A正确;
水面四边形EFGH是矩形,随着倾斜程度的不同,边长EF有变化,面积也随之变化,B错误;
棱A1D1∥EH,由线面平行的判定定理得A1D1始终与水面EFGH平行,C正确;
在旋转过程中,水的体积保持不变,所以当E∈AA1时,四棱柱ABFE-DCGH的体积不变,
高BC不变,梯形ABFE的面积也不变,即S=(AE+BF)·AB是定值,即AE+BF是定值,D正确.
20、【答案】a
【解析】∵MN∥平面AC,平面PMN∩平面AC=PQ,∴MN∥PQ.∵MN∥A1C1∥AC,∴PQ∥AC.
∵AP=,∴DP=DQ=.∴PQ=×=a.
21、[解] 如图,连接BD交AC于点O1,连接OM.
因为PC∥平面MEF,PC 平面PAC,平面PAC∩平面MEF=OM,
所以PC∥OM,所以=.
在菱形ABCD中,因为E,F分别为边BC,CD的中点,所以=.
又AO1=O1C,所以==,
故PM∶MA=1∶3,即点M为线段PA上靠近点P的四等分点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
8.5.2 直线与平面平行
班级 姓名
学习目标
1.掌握直线与平面平行的判定定理和性质定理,并能利用这两个定理解决空间中的平行关系问题.
2.利用直线与平面平行的判定定理和性质定理证明空间平行问题.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 一、直线与平面平行的判定定理文字语言如果______一条直线与此平面内的一条直线______,那么该直线与此平面平行图形语言符号语言 _____________________________________________________________作用证明直线与平面________【即时训练1】(多选题)如图,点A,B,C,M,N是正方体的顶点或所在棱的中点,则下列各图中能满足平面的是( )A B C D
阅读教材,完成右边的内容 二、直线与平面平行的性质定理文字语言一条直线与一个平面_____,如果过该直线的平面与此平面________,那么该直线与交线______图形语言符号语言 ____________________________________________________作用证明两条直线______【即时训练2】(多选题)下列选项中,正确的是( )A.如果两个平面平行,那么分别在这两个平面内任取两条直线,两直线平行B.如果两个平面平行,那么其中一个平面内的直线与另一平面平行C.如果一个平面内的一个锐角的两边分别平行于另一个平面内的一个角的两边,那么这两个平面平行D.如果一个平面内有无数条直线平行于另一个平面,那么这两个平面平行
直线与平面平行的判定 例1、如图,在正方体ABCD-A1B1C1D1中,E,F,G分别是BC,CC1,BB1的中点,求证:EF∥平面AD1G.例2、如图,在直三棱柱ABC-A1B1C1中,点D是AB的中点,求证:BC1∥平面CA1D.例3、如图,已知四棱锥P-ABCD的底面为矩形,M,N分别是AB,PC的中点.求证:MN∥平面PAD.例4、如图,在正方体ABCD A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥平面AA1B1B.
直线与平面平行的性质 例5、如图,用平行于四面体ABCD的一组对棱AB,CD的平面截此四面体.求证:截面MNPQ是平行四边形.例6、如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,AC与BD交于点O,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH. INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMAT INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\8-201.TIF" \* MERGEFORMATINET INCLUDEPICTURE "D:\\2019\\同步\\数学\\人A必修第二册(新教材)\\数学 人A 必修第二册(新教材)最新(加双选)\\8-201.TIF" \* MERGEFORMATINET
课后作业
一、基础训练题
1.下列命题中正确的是( )
A.平行于同一平面的两条直线平行
B.同时与两条异面直线平行的平面有无数多个
C.如果一条直线上有两点在一个平面外,那么这条直线与这个平面平行
D.若直线l不在平面α内,则l∥α
2.如图,在正方体ABCD-A1B1C1D1中,与平面D1AC不平行的是( )
A.A1B B.BB1
C.BC1 D.A1C1
3.如图,下列正三棱柱ABC-A1B1C1中,若M,N,P分别为其所在棱的中点,则不能得出AB∥平面MNP的是( )
4.(多选题)若直线a平行于平面α,则下列结论正确的是( )
A.直线a与平面α无交点
B.直线a平行于平面α内的所有直线
C.平面α内有无数条直线与直线a平行
D.平面α内存在无数条直线与直线a为异面直线
5.在长方体ABCD A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D1、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有( )
A.2个 B.3个 C.4个 D.5个
6.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,H,G分别为BC,CD的中点,则( )
A.BD∥平面EFG,且四边形EFGH是平行四边形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是平行四边形
D.EH∥平面ADC,且四边形EFGH是梯形
7.(多选题)一几何体的平面展开图如下左图所示(顶点P在展开图中分别为P1,P2,P3,P4),其中四边形ABCD为正方形,E,F分别为P4B,P1C的中点,在此几何体中,给出的下列结论中正确的是( )
A.直线AE与直线BF异面 B.直线AE与直线DF异面
C.直线EF∥平面PAD D.直线EF∥平面ABCD
8.如上右图,直线a∥平面α,A是平面α的另一侧的点,点B,C,D∈a,线段AB,AC,AD分别交α于点E,F,G,若BD=4,CF=4,AF=5,则EG=( )
A. B.
C. D.
9.对于直线m,n和平面α,下面命题中的真命题是( )
A.如果m α,n α,m,n是异面直线,那么n∥α
B.如果m α,n与α相交,那么m,n是异面直线
C.如果m α,n∥α,m,n共面,那么m∥n
D.如果m∥α,n∥α,m,n共面,那么m∥n
10.如图,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出以下结论:
①OM∥PD;
②OM∥平面PCD;
③OM∥平面PDA;
④OM∥平面PBA;
⑤OM∥平面PBC.其中正确的个数是( )
A.1 B.2 C.3 D.4
11.如下左图,ABCD A1B1C1D1是正方体,若过A,C,B1三点的平面与底面A1B1C1D1的交线为l,则l与AC的关系是________.
12.如上右图,P为 ABCD所在平面外一点,E为AD的中点,F为PC上一点,当PA∥平面EBF时,=________.
13.如图所示,已知四边形ABCD是正方形,四边形ACEF是矩形,M是线段EF的中点.求证:AM∥平面BDE.
14.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE,若存在,指出点M的位置,并证明你的结论.
15.如图所示,在三棱柱ABC-A1B1C1中,D是棱CC1的中点,E是棱AB的中点,证明:DE∥平面AB1C1.
16.如图所示,四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.
(1)求证:AB∥平面EFGH,CD∥平面EFGH;
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
二、综合训练题
17.a,b是两条异面直线,下列结论正确的是( )
A.过不在a,b上的任一点,可作一个平面与a,b平行
B.过不在a,b上的任一点,可作一条直线与a,b相交
C.过不在a,b上的任一点,可作一条直线与a,b都平行
D.过a可以并且只可以作一个平面与b平行
18.如图,四棱锥S ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )
A.2+ B.3+
C.3+2 D.2+2
19.(多选题)如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,下列说法正确的是( )
A.水的部分始终呈棱柱状
B.水面四边形EFGH的面积不改变
C.棱A1D1始终与水面EFGH平行
D.当E∈AA1时,AE+BF是定值
三、能力提升题
20.如图所示,ABCD A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
21.如图,已知E,F分别是菱形ABCD的边BC,CD的中点,EF与AC交于点O,点P在平面ABCD外,M是线段PA上一动点,若PC∥平面MEF,试确定点M的位置.
8.5.2 直线与平面平行
参考答案
例1、【证明】连接BC1(图略),在△BCC1中,
∵E,F分别为BC,CC1的中点,∴EF∥BC1,
又∵AB∥A1B1∥D1C1,且AB=A1B1=D1C1,
∴四边形ABC1D1是平行四边形,
∴BC1∥AD1,∴EF∥AD1,又EF 平面AD1G,
AD1 平面AD1G,∴EF∥平面AD1G.
例2、【证明】如图所示,连接AC1交A1C于点O,连接OD,则O是AC1的中点.
又∵点D是AB的中点,∴OD∥BC1.
又∵OD 平面CA1D,BC1 平面CA1D,
∴BC1∥平面CA1D.
例3、【证明】如图,取PD中点E,连接AE,NE.
∵N,E分别为PC,PD的中点,∴NECD.
又∵M为AB中点,底面ABCD为矩形,
∴AMCD,∴AMNE.
∴四边形AMNE为平行四边形,∴MN∥AE.
又∵MN 面PAD,AE 面PAD,
∴MN∥面PAD.
例4、【证明】法一:如图,作ME∥BC,交BB1于点E,作NF∥AD,
交AB于点F,连接EF,则EF 平面AA1B1B,
且=,=.
∵在正方体ABCD A1B1C1D1中,CM=DN,B1C=BD,∴B1M=NB.
∴==.又AD=BC,
∴ME=NF.又ME∥BC∥AD∥NF,
∴四边形MEFN为平行四边形.∴MN∥EF.
∵MN 平面AA1B1B,EF 平面AA1B1B,
∴MN∥平面AA1B1B.
法二:如图②,连接CN并延长交BA所在直线于点P,连接B1P,则B1P 平面AA1B1B.
∵△NDC∽△NBP,∴=.
又CM=DN,B1C=BD,
∴==.∴MN∥B1P.
∵MN 平面AA1B1B,B1P 平面AA1B1B,
∴MN∥平面AA1B1B.
例5、【证明】因为AB∥平面MNPQ,平面ABC∩平面MNPQ=MN,且AB 平面ABC,
所以由线面平行的性质定理,知AB∥MN.
同理,AB∥PQ,
所以MN∥PQ.同理可得MQ∥NP.
所以截面MNPQ是平行四边形.
例6、【证明】连接MO.
∵四边形ABCD是平行四边形,
∴O是AC的中点.又∵M是PC的中点,∴AP∥OM.
又∵AP 平面BDM,OM 平面BDM,∴AP∥平面BDM.
又∵AP 平面APGH,平面APGH∩平面BDM=GH,∴AP∥GH.
课后作业
1、【答案】B
2、【答案】B
【解析】∵A1B∥D1C,且D1C 平面D1AC,A1B 平面D1AC,∴A1B∥平面D1AC.
∵BC1∥AD1,且AD1 平面D1AC,BC1 平面D1AC,∴BC1∥平面D1AC.
∵A1C1∥AC,且AC 平面D1AC,A1C1 平面D1AC,∴A1C1∥平面D1AC.
3、【答案】C
【解析】在A、B中,易知AB∥A1B1∥MN,由线面平行的判定定理得AB∥平面MNP;在D中,易知AB∥PN,由线面平行的判定定理得AB∥平面MNP.在C中,易知A1B1与平面MNP相交,由AB∥A1B1知AB与平面MNP相交,故选C.
4、【答案】ACD
【解析】由题意知,直线a平行于平面α.直线a与平面α无交点,A正确;直线a与平面α内的直线可能平行或异面,B不正确;平面α内有无数条直线与直线a平行,C正确;平面α内存在无数条直线与直线a成异面直线,D正确.故选ACD.
5、【答案】B
【解析】如图所示,结合图形可知AA1∥平面BC1,AA1∥平面DC1,AA1∥平面BB1D1D.
6、【答案】B
【解析】如图,由题意,得EF∥BD,且EF=BD,HG∥BD,且HG=BD,∴EF∥HG且EF≠HG,∴四边形EFGH是梯形.又EF∥BD,EF 平面BCD,BD 平面BCD,
∴EF∥平面BCD,分析知EH与平面ADC不平行.故选B.
7、【答案】ACD
【解析】如图,将平面展开图还原为几何体,显然AE,BF异面,可知A正确;
易得EF∥BC,又BC∥AD,∴EF∥AD,又EF 平面PAD,AD 平面PAD,
∴EF∥平面PAD,可知C正确;
易知四边形AEFD为梯形,可知B错误;∵EF∥BC,BC 平面ABCD,EF 平面ABCD,
∴EF∥平面ABCD,故D正确.故选ACD.
8、【答案】B
【解析】∵a∥α,α∩平面ABD=EG,a 平面ABD,∴a∥EG,即BD∥EG,
∴==,则EG===.故选B.
9、【答案】C
【解析】对于A,如果m α,n α,m,n是异面直线,则n∥α或n与α相交,故A错;对于B,如果m α,n与α相交,则m,n相交或是异面直线,故B错;对于C,如果m α,n∥α,m,n共面,由线面平行的性质定理,可得m∥n,故C对;对于D,如果m∥α,n∥α,m,n共面,则m∥n或m,n相交,故D错.
10、【答案】C
【解析】由题意知,OM∥PD,PD 平面PCD,PD 平面PDA,OM 平面PCD,OM 平面PDA,所以OM∥平面PCD,OM∥平面PDA.故选C.
11、【答案】平行
【解析】连接A1C1(图略),∵AC∥A1C1,∴AC∥平面A1B1C1D1,
又∵AC 平面AB1C,平面AB1C∩平面A1B1C1D1=l,∴AC∥l.
12、【答案】
【解析】连接AC交BE于G,连接FG,因为PA∥平面EBF,
PA 平面PAC,平面PAC∩平面BEF=FG,所以PA∥FG,所以=.
又因为AD∥BC,E为AD的中点,所以==,所以=.
13、【证明】如图,记AC与BD的交点为O,连接OE.
∵O,M分别是AC,EF的中点,四边形ACEF是矩形,
∴EM∥OA,且EM=OA,
∴四边形AOEM是平行四边形,∴AM∥OE.
又OE 平面BDE,AM 平面BDE,
∴AM∥平面BDE.
14、[解] 存在点M,如图,当点M是线段AE的中点时,PM∥平面BCE.
证明如下:取BE的中点N,连接CN,MN,则MN∥AB且MN=AB.
又PC∥AB且PC=AB,所以MN∥PC且MN=PC,
所以四边形MNCP为平行四边形,所以PM∥CN.
因为PM 平面BCE,CN 平面BCE,
所以PM∥平面BCE.
15、【证明】如图,取AB1的中点H,连接EH,HC1.∵E是棱AB的中点,∴EH∥BB1,且EH=BB1.
∵D是棱CC1的中点,∴DC1=CC1,
又BB1∥CC1,且BB1=CC1,∴DC1∥BB1,且DC1=BB1,
∴EH∥DC1,且EH=DC1,
∴四边形EHC1D为平行四边形,∴DE∥HC1.
又∵HC1 平面AB1C1,DE 平面AB1C1,
∴DE∥平面AB1C1.
16、[解析] (1)证明:∵四边形EFGH为平行四边形,∴EF∥HG.
∵HG 平面ABD,EF 平面ABD,∴EF∥平面ABD.∵EF 平面ABC,
平面ABD∩平面ABC=AB,∴EF∥AB.
又EF 平面EFGH,AB 平面EFGH.∴AB∥平面EFGH.同理可证CD∥平面EFGH.
(2)设EF=x(0
又0
【解析】A错,若点与a所确定的平面与b平行时,就不能使这个平面与a平行了.
B错,若点与a所确定的平面与b平行时,就不能作一条直线与a,b相交.
C错,假如这样的直线存在,根据基本事实4就可有a∥b,这与a,b异面矛盾.
D正确,在a上任取一点A,过A点做直线c∥b,则c与a确定一个平面与b平行,这个平面是唯一的.
18、【答案】C
【解析】由AB=BC=CD=DA=2,得AB∥CD,即AB∥平面DCFE,
∵平面SAB∩平面DCFE=EF,∴AB∥EF.∵E是SA的中点,
∴EF=1,DE=CF=.∴四边形DEFC的周长为3+2.
19、【答案】ACD
【解析】将该四棱柱绕BC旋转,面ABFE与面DCGH始终平行且全等,其余面为四边形,且相邻棱平行,所以ABFE-DCGH始终呈棱柱状,A正确;
水面四边形EFGH是矩形,随着倾斜程度的不同,边长EF有变化,面积也随之变化,B错误;
棱A1D1∥EH,由线面平行的判定定理得A1D1始终与水面EFGH平行,C正确;
在旋转过程中,水的体积保持不变,所以当E∈AA1时,四棱柱ABFE-DCGH的体积不变,
高BC不变,梯形ABFE的面积也不变,即S=(AE+BF)·AB是定值,即AE+BF是定值,D正确.
20、【答案】a
【解析】∵MN∥平面AC,平面PMN∩平面AC=PQ,∴MN∥PQ.∵MN∥A1C1∥AC,∴PQ∥AC.
∵AP=,∴DP=DQ=.∴PQ=×=a.
21、[解] 如图,连接BD交AC于点O1,连接OM.
因为PC∥平面MEF,PC 平面PAC,平面PAC∩平面MEF=OM,
所以PC∥OM,所以=.
在菱形ABCD中,因为E,F分别为边BC,CD的中点,所以=.
又AO1=O1C,所以==,
故PM∶MA=1∶3,即点M为线段PA上靠近点P的四等分点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
