2015秋鲁教版数学八上4.2图形的旋转课件
文档属性
| 名称 | 2015秋鲁教版数学八上4.2图形的旋转课件 |  | |
| 格式 | zip | ||
| 文件大小 | 608.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-08 19:34:17 | ||
图片预览









文档简介
课件32张PPT。4.2 图形的旋转(2课时)1.经历对生活中的旋转现象有关图形进行观察、分析、欣赏、以及动手操作、画图等过程,掌握有关画图的操作技能,发展初步的审美能力,增强对图形欣赏的意识.
2.通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质.【定义】
在平面内,将一个图形绕一个定点按某个方向
转动一个角度,这样的图形运动称为_____,这个定
点称为________,转动的角称为_______. 旋转旋转中心旋转角旋转不改变图形的形状和大小. (即旋转前后的两个图形是全等形)【例1】如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移 动到什么位置?
3.AO与DO的长有什么关系? BO与EO呢?
4.∠AOD与∠BOE有什么大小 关系?BACODEF【例题】【解析】1.旋转中心是O点,旋转角是∠AOD.旋转角还可以是∠BOE.
2.A旋转到点D的位置,点B旋转到点E的位置.
3.钟表的指针长短、形状没有变化,所以OA与OD是相等的.同样,线段OB与OE是相等的.
4.因为四边形AOBC绕O点旋转到四边形DOEF的位置,在旋转的过程中,图形上的每个点同时都按相同的方向旋转相同的角度,所以∠AOD与∠BOE是相等的. 经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.对应点到旋转中心的距离相等.任意一组对应点与旋转中心的连线所成的角都等于旋转角,对应线段相等,对应角相等.旋转的基本性质:四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
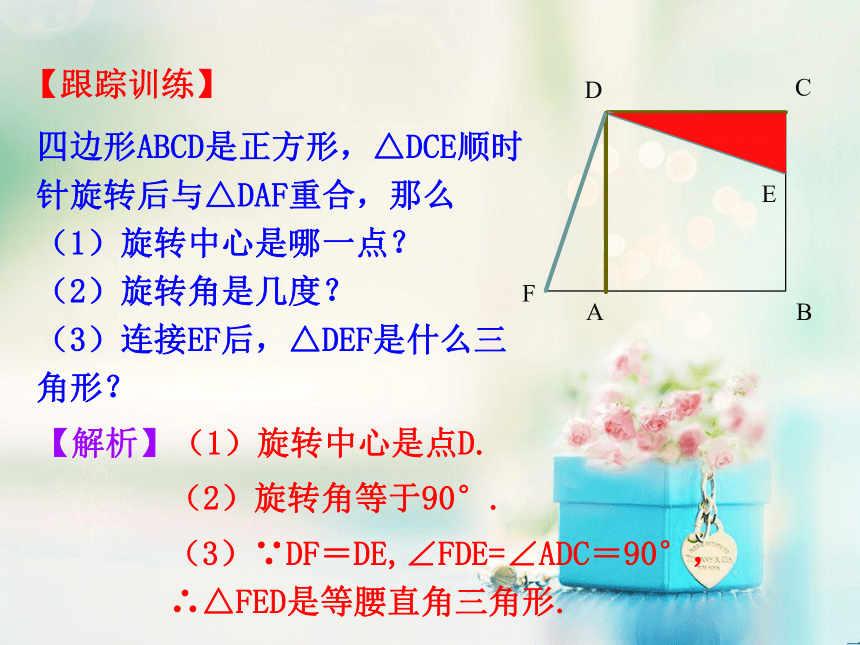
(3)连接EF后,△DEF是什么三角形?【解析】(1)旋转中心是点D.(2)旋转角等于90°.(3)∵DF=DE,∠FDE=∠ADC=90°, ∴△FED是等腰直角三角形.【跟踪训练】【例2】钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
【解析】(1)它的旋转中心是钟表的轴心;
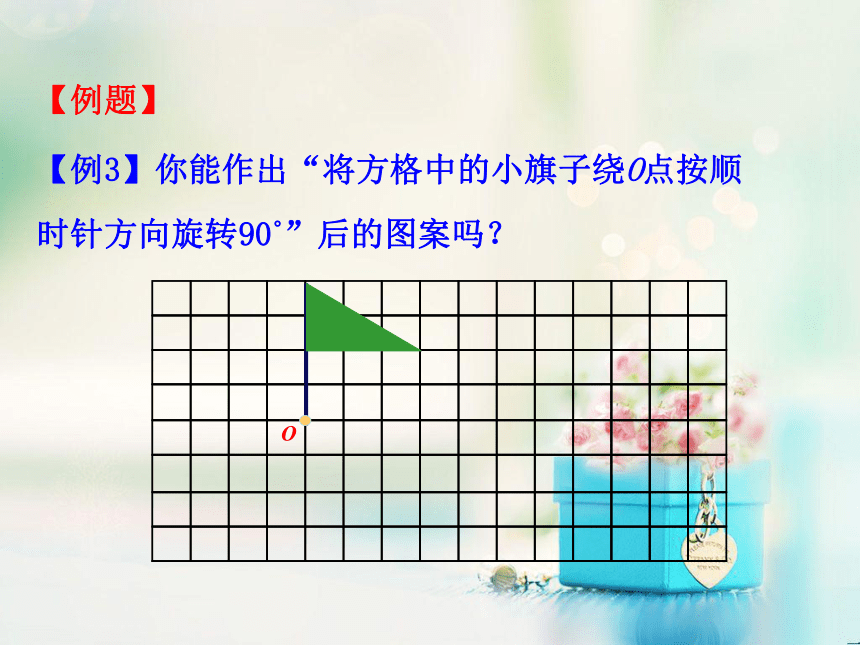
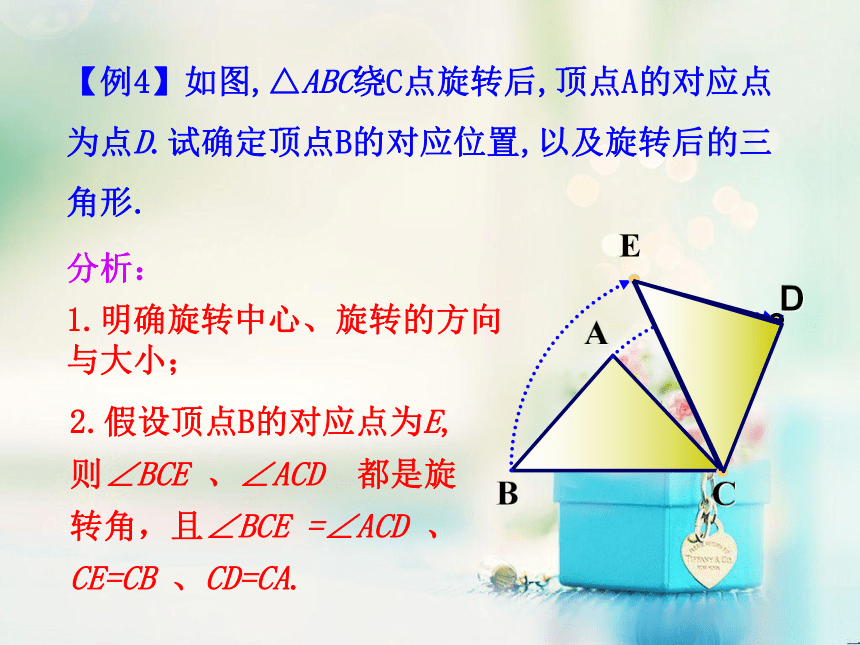
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为【例题】【例3】你能作出“将方格中的小旗子绕O点按顺时针方向旋转90?”后的图案吗?【例题】O【解析】在原图上找了四个点即O点、A点、B点、C点,四个点是表示这面小旗子的关键点.因为旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所组成的旋转角彼此相等,所以根据已知:要把这面小旗绕O点按顺时针旋转90°.在方格中找到点A、B、C的对应点A1、B1、C1,然后连接,就得到了所求作的图形.OA1ACBB1C1【例4】如图,△ABC绕C点旋转后,顶点A的对应点为点D.试确定顶点B的对应位置,以及旋转后的三角形.ABCD分析:1.明确旋转中心、旋转的方向与大小;2.假设顶点B的对应点为E,则∠BCE 、∠ACD 都是旋转角,且∠BCE =∠ACD 、CE=CB 、CD=CA.EABCD【解析】作法一(1)连接CD;(2)以CB 为一边作∠BCF,使
得∠BCF=∠ACD; E(3)在射线CF上截取CE=CB;(4)连接DE .则△DEC就是△ABC绕C点旋转后的图形.FABCDE(1)以点C为圆心、CB长为半径画弧 ,(2)以点D为圆心、AB长为半径画弧 ,(3)两弧的交点E 即为点B的
对应点.(4)连接 CE 、ED、DC.【解析】作法二则△DEC就是△ABC绕C点旋转后的图形.在下图中,将大写字母N绕它右下侧的顶点按顺时针方向旋转 90? ,作出旋转后的图案.【跟踪训练】1. 如图,在等腰直角△ABC中∠B=900,将△ ABC绕顶点A逆时针方向旋转600 ,后得到△ A B′C′,则∠BAC′等于( )A.60° B.105°
C.120° D.135°【解析】选B.如题干图,将△ ABC绕顶点A逆时针方向旋转60°,∴∠CAC′=60°,∵△ ABC是等腰直角三角形,∴∠BAC=45°, ∴∠BAC′= ∠CAC′+ ∠BAC=105°2.(上海·中考)已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为_____.【解析】题目里只说“旋转”,并没有说顺时针还是逆时针,而且说的是“直线BC上的点”,所以有两种情况如图所示:F1C=1,F2B=DE=2,F2C=F2B+BC=5.
答案:1或53.△ABC是等边三角形,△ABP顺时针旋转后能与△CBP′重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连接PP′后,△BPP′是
什么三角形?【解析】(1)旋转中心是点B.(2)旋转角等于60°.(3)∵BP=BP′,∠PBP′=∠ABC=60°,∴△BPP′是等边三角形(有一个角等于60°的等腰三角形是等边三角形).4.在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°.
求证:AD平分∠CDE.【证明】如图连接AC,将△ABC绕点A旋转∠BAE的度数到△AEF的位置,
∵AB=AE,∴AB与AE重合.
∵∠ABC+∠AED=180°,且∠AEF=
∠ABC, ∴∠AEF+∠AED=180°
∴D,E,F三点在一直线上,AC=AF,BC=EF.
在△ADC与△ADF中,
∵DF=DE+EF=DE+BC=CD.,AF=AC,AD=AD
∴△ADC≌△ADF(SSS),
∴∠ADC=∠ADF,
即:AD平分∠CDE.【规律方法】利用旋转解决问题紧紧抓住旋转的性质,经过旋转,旋转角彼此相等,对应点到旋转中心的距离相等.构造全等,是证明角、线段相等的常用方法. 1.旋转中心在旋转过程中保持不动.
2.图形中每一点都绕着旋转中心旋转了同样大小的角度,对应的点到旋转中心的距离相等,对应线段、角均相等.
3.旋转一定角度后能与自身重合.
4.旋转作图要找准原图形的位置、旋转中心、旋转角.1.将一个四边形进行旋转可得到如图所示图形
(1)这个四边形旋转了几次?
(2)每次旋转了多少度?【解析】(1)旋转5次得到.(2)60°【跟踪训练】2.在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.GACBDEFHGACBDEFH【解析】方法一:整个图形可以看成是图形的八分之一绕中心位置,按照同一方向连续旋转45°、90°、135°、180°、225°、270°、315°前后的图形共同组成的.GACBDFH方法二:整个图形也可以看成是图形的四分之一绕中心位置连续旋转90°、180°、270°前后的图形共同组成的.EGACBDFH方法三:整个图形还可以看成是图形的二分之一绕中心位置旋转180°前后的图形共同组成的.E 成功的人是跟别人学习经验,失败的人只跟自己学习经验。
2.通过具体实例认识旋转,理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质.【定义】
在平面内,将一个图形绕一个定点按某个方向
转动一个角度,这样的图形运动称为_____,这个定
点称为________,转动的角称为_______. 旋转旋转中心旋转角旋转不改变图形的形状和大小. (即旋转前后的两个图形是全等形)【例1】如图所示,如果把钟表的指针看作四边形AOBC,它绕O点按顺时针方向旋转得到四边形DOEF.在这个旋转过程中:1.旋转中心是什么?旋转角是什么?
2.经过旋转,点A,B分别移 动到什么位置?
3.AO与DO的长有什么关系? BO与EO呢?
4.∠AOD与∠BOE有什么大小 关系?BACODEF【例题】【解析】1.旋转中心是O点,旋转角是∠AOD.旋转角还可以是∠BOE.
2.A旋转到点D的位置,点B旋转到点E的位置.
3.钟表的指针长短、形状没有变化,所以OA与OD是相等的.同样,线段OB与OE是相等的.
4.因为四边形AOBC绕O点旋转到四边形DOEF的位置,在旋转的过程中,图形上的每个点同时都按相同的方向旋转相同的角度,所以∠AOD与∠BOE是相等的. 经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.对应点到旋转中心的距离相等.任意一组对应点与旋转中心的连线所成的角都等于旋转角,对应线段相等,对应角相等.旋转的基本性质:四边形ABCD是正方形,△DCE顺时针旋转后与△DAF重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连接EF后,△DEF是什么三角形?【解析】(1)旋转中心是点D.(2)旋转角等于90°.(3)∵DF=DE,∠FDE=∠ADC=90°, ∴△FED是等腰直角三角形.【跟踪训练】【例2】钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
【解析】(1)它的旋转中心是钟表的轴心;
(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为【例题】【例3】你能作出“将方格中的小旗子绕O点按顺时针方向旋转90?”后的图案吗?【例题】O【解析】在原图上找了四个点即O点、A点、B点、C点,四个点是表示这面小旗子的关键点.因为旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所组成的旋转角彼此相等,所以根据已知:要把这面小旗绕O点按顺时针旋转90°.在方格中找到点A、B、C的对应点A1、B1、C1,然后连接,就得到了所求作的图形.OA1ACBB1C1【例4】如图,△ABC绕C点旋转后,顶点A的对应点为点D.试确定顶点B的对应位置,以及旋转后的三角形.ABCD分析:1.明确旋转中心、旋转的方向与大小;2.假设顶点B的对应点为E,则∠BCE 、∠ACD 都是旋转角,且∠BCE =∠ACD 、CE=CB 、CD=CA.EABCD【解析】作法一(1)连接CD;(2)以CB 为一边作∠BCF,使
得∠BCF=∠ACD; E(3)在射线CF上截取CE=CB;(4)连接DE .则△DEC就是△ABC绕C点旋转后的图形.FABCDE(1)以点C为圆心、CB长为半径画弧 ,(2)以点D为圆心、AB长为半径画弧 ,(3)两弧的交点E 即为点B的
对应点.(4)连接 CE 、ED、DC.【解析】作法二则△DEC就是△ABC绕C点旋转后的图形.在下图中,将大写字母N绕它右下侧的顶点按顺时针方向旋转 90? ,作出旋转后的图案.【跟踪训练】1. 如图,在等腰直角△ABC中∠B=900,将△ ABC绕顶点A逆时针方向旋转600 ,后得到△ A B′C′,则∠BAC′等于( )A.60° B.105°
C.120° D.135°【解析】选B.如题干图,将△ ABC绕顶点A逆时针方向旋转60°,∴∠CAC′=60°,∵△ ABC是等腰直角三角形,∴∠BAC=45°, ∴∠BAC′= ∠CAC′+ ∠BAC=105°2.(上海·中考)已知正方形ABCD中,点E在边DC上,DE=2,EC=1,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为_____.【解析】题目里只说“旋转”,并没有说顺时针还是逆时针,而且说的是“直线BC上的点”,所以有两种情况如图所示:F1C=1,F2B=DE=2,F2C=F2B+BC=5.
答案:1或53.△ABC是等边三角形,△ABP顺时针旋转后能与△CBP′重合,那么
(1)旋转中心是哪一点?
(2)旋转角是几度?
(3)连接PP′后,△BPP′是
什么三角形?【解析】(1)旋转中心是点B.(2)旋转角等于60°.(3)∵BP=BP′,∠PBP′=∠ABC=60°,∴△BPP′是等边三角形(有一个角等于60°的等腰三角形是等边三角形).4.在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°.
求证:AD平分∠CDE.【证明】如图连接AC,将△ABC绕点A旋转∠BAE的度数到△AEF的位置,
∵AB=AE,∴AB与AE重合.
∵∠ABC+∠AED=180°,且∠AEF=
∠ABC, ∴∠AEF+∠AED=180°
∴D,E,F三点在一直线上,AC=AF,BC=EF.
在△ADC与△ADF中,
∵DF=DE+EF=DE+BC=CD.,AF=AC,AD=AD
∴△ADC≌△ADF(SSS),
∴∠ADC=∠ADF,
即:AD平分∠CDE.【规律方法】利用旋转解决问题紧紧抓住旋转的性质,经过旋转,旋转角彼此相等,对应点到旋转中心的距离相等.构造全等,是证明角、线段相等的常用方法. 1.旋转中心在旋转过程中保持不动.
2.图形中每一点都绕着旋转中心旋转了同样大小的角度,对应的点到旋转中心的距离相等,对应线段、角均相等.
3.旋转一定角度后能与自身重合.
4.旋转作图要找准原图形的位置、旋转中心、旋转角.1.将一个四边形进行旋转可得到如图所示图形
(1)这个四边形旋转了几次?
(2)每次旋转了多少度?【解析】(1)旋转5次得到.(2)60°【跟踪训练】2.在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.GACBDEFHGACBDEFH【解析】方法一:整个图形可以看成是图形的八分之一绕中心位置,按照同一方向连续旋转45°、90°、135°、180°、225°、270°、315°前后的图形共同组成的.GACBDFH方法二:整个图形也可以看成是图形的四分之一绕中心位置连续旋转90°、180°、270°前后的图形共同组成的.EGACBDFH方法三:整个图形还可以看成是图形的二分之一绕中心位置旋转180°前后的图形共同组成的.E 成功的人是跟别人学习经验,失败的人只跟自己学习经验。
