8.6.2 直线与平面垂直 课件(共22张PPT)
文档属性
| 名称 | 8.6.2 直线与平面垂直 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 15:11:29 | ||
图片预览



文档简介
(共22张PPT)
8.6.2 直线与平面垂直
单击此处输入你的副标题,请尽量言简意赅的阐述观点。
问题1:直线与平面呈现了什么样的位置关系?
问题2:阳光下直立于地面的旗杆AB与它在
地面的影子BC位置关系如何?
18世纪法国数学家克莱罗在《几何基础》中给出线面垂直的
直观解释:一条直线不向平面上的任何一面倾斜.
A
B
α
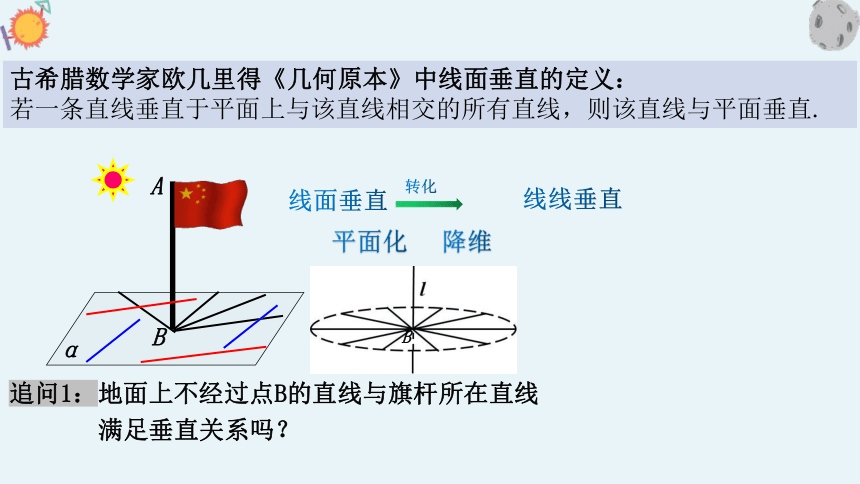
古希腊数学家欧几里得《几何原本》中线面垂直的定义:
若一条直线垂直于平面上与该直线相交的所有直线,则该直线与平面垂直.
A
B
α
追问1:地面上不经过点B的直线与旗杆所在直线
满足垂直关系吗?
平面化
降维
线面垂直
线线垂直
转化
B
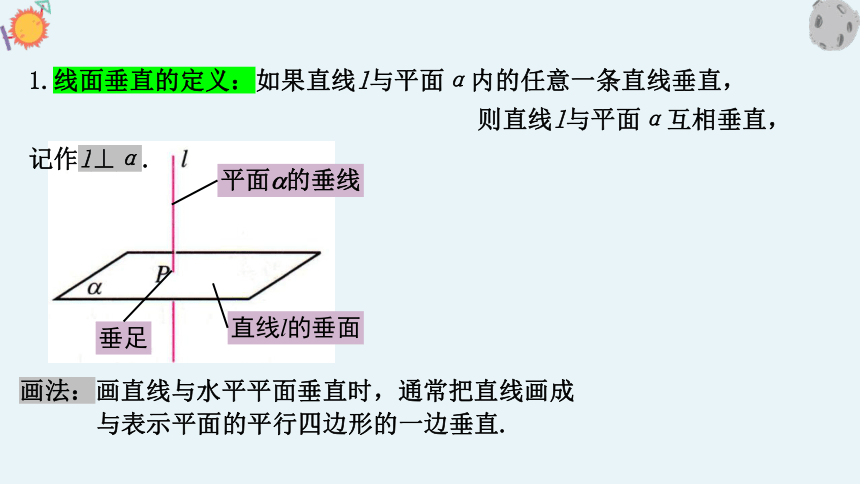
画法:画直线与水平平面垂直时,通常把直线画成
与表示平面的平行四边形的一边垂直.
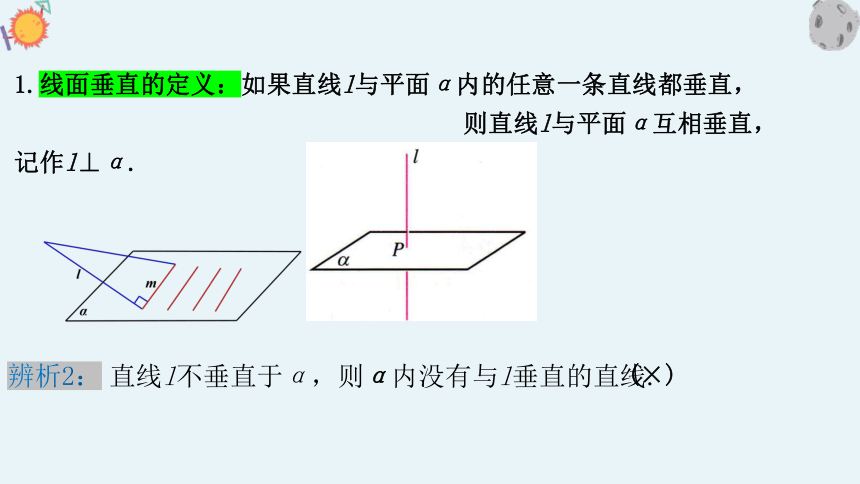
1.线面垂直的定义:如果直线l与平面α内的任意一条直线垂直,
则直线l与平面α互相垂直,记作l⊥α.
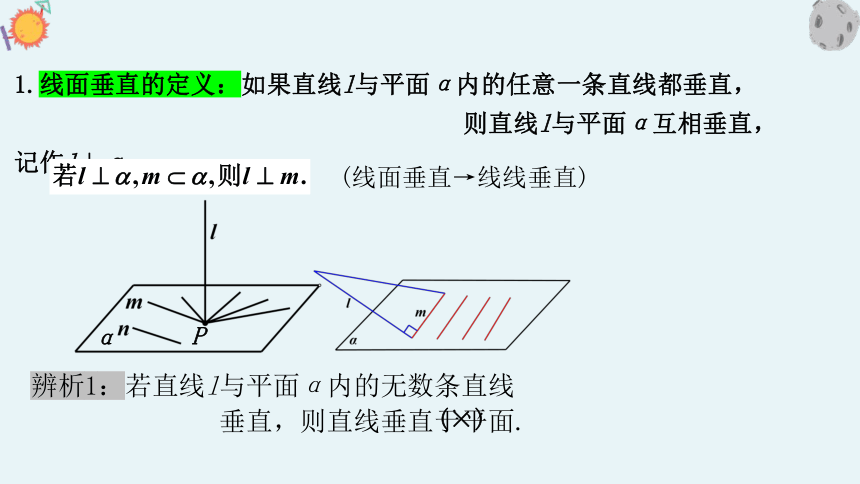
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
P
α
辨析1:若直线l与平面α内的无数条直线
垂直,则直线垂直于平面.
(×)
(线面垂直→线线垂直)
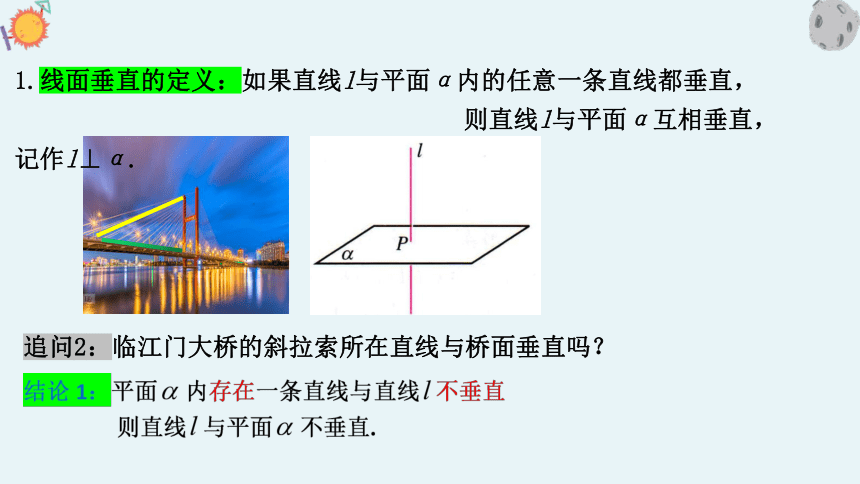
追问2:临江门大桥的斜拉索所在直线与桥面垂直吗?
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
辨析2:
直线l不垂直于α,则α内没有与l垂直的直线.
(×)
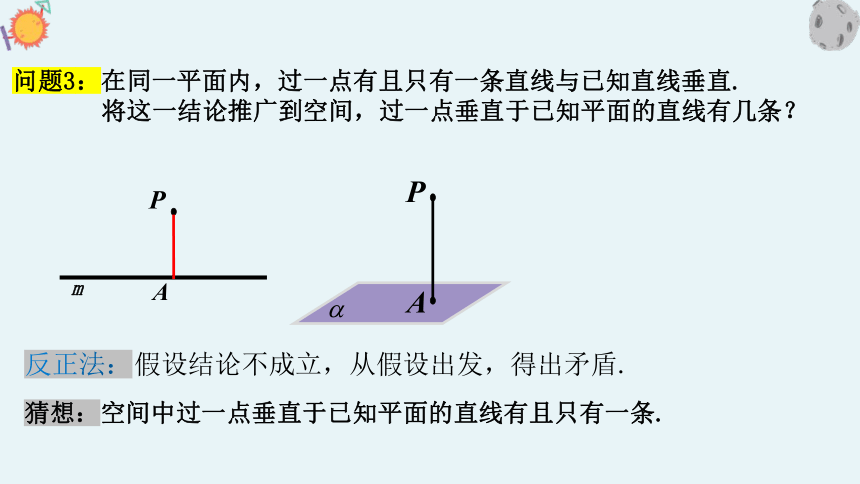
问题3:在同一平面内,过一点有且只有一条直线与已知直线垂直.
将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
m
假设结论不成立,从假设出发,得出矛盾.
反正法:
猜想:空间中过一点垂直于已知平面的直线有且只有一条.
反证法:假设过点P有两条直线a,b垂直于同一平面α.
设两直线确定的平面为β,且α∩β=c,所以c β.
由线面垂直的定义,知a⊥c,b⊥c,矛盾.
所以假设不成立,原命题成立.
已知:P是空间一点,直线a过点P,且a⊥α.
求证:a是唯一存在的.
问题3:在同一平面内,过一点有且只有一条直线与已知直线垂直.
将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
结论2:过一点垂直于已知平面的直线有且只有一条.
垂线段:PA
点P到平面的距离:PA的长度
如:棱锥的高就是棱锥
的顶点到底面的距离.
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
问题4:用定义来判断线面垂直方便吗?
无限证明
有限证明
转化
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
追问1:一条直线至少与平面内的几条直线垂直,
才能够判定直线与平面垂直?
一条
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
追问1:一条直线至少与平面内的几条直线垂直,
才能够判定直线与平面垂直?
两条
探究:如图8.6-10,准备一块三角形的纸片ABC,过 ABC 的顶点A翻折纸片,
得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).
请你动手操作并思考:
(1)折痕AD与桌面垂直吗
(2)如何翻折才能使折痕AD与桌面垂直?
探究:如图8.6-10,准备一块三角形的纸片ABC,过 ABC 的顶点A翻折纸片,
得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).
请你动手操作并思考:
(1)折痕AD与桌面垂直吗
(2)如何翻折才能使折痕AD与桌面垂直?
猜想:当折痕AD⊥BC且翻折后BD与CD不在一条直线上时,
折痕AD与桌面所在的平面垂直.
追问2:如何验证折痕AD与桌面垂直?
A
B
D
C
m
探究成果:一条直线与平面内的两条相交直线垂直,
则直线与该平面垂直.
2.线面垂直的判定定理:一条直线与平面内的两条相交直线垂直,
那么直线与该平面垂直.
②符号语言:
①图形语言:
③本质:线线垂直→线面垂直
关键: 证两个线线垂直
m
n
P
问题5:两平行线中的一条垂直于平面,另一条是否也垂直于平面?
符号语言:
m
n
线线平行
线面垂直
传递
平行性质
例1
面面平行
线面垂直
传递
平行性质
变式 如图
1.直线与平面垂直
定义
判定定理
平行性质
证明方法
2.思想方法
(类比、化归)
线线垂直
线面垂直
转化
无限证明
有限证明
转化
文字语言
图形语言
转化
符号语言
转化
平行关系
垂直关系
转化
8.6.2 直线与平面垂直
单击此处输入你的副标题,请尽量言简意赅的阐述观点。
问题1:直线与平面呈现了什么样的位置关系?
问题2:阳光下直立于地面的旗杆AB与它在
地面的影子BC位置关系如何?
18世纪法国数学家克莱罗在《几何基础》中给出线面垂直的
直观解释:一条直线不向平面上的任何一面倾斜.
A
B
α
古希腊数学家欧几里得《几何原本》中线面垂直的定义:
若一条直线垂直于平面上与该直线相交的所有直线,则该直线与平面垂直.
A
B
α
追问1:地面上不经过点B的直线与旗杆所在直线
满足垂直关系吗?
平面化
降维
线面垂直
线线垂直
转化
B
画法:画直线与水平平面垂直时,通常把直线画成
与表示平面的平行四边形的一边垂直.
1.线面垂直的定义:如果直线l与平面α内的任意一条直线垂直,
则直线l与平面α互相垂直,记作l⊥α.
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
P
α
辨析1:若直线l与平面α内的无数条直线
垂直,则直线垂直于平面.
(×)
(线面垂直→线线垂直)
追问2:临江门大桥的斜拉索所在直线与桥面垂直吗?
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
1.线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直,记作l⊥α.
辨析2:
直线l不垂直于α,则α内没有与l垂直的直线.
(×)
问题3:在同一平面内,过一点有且只有一条直线与已知直线垂直.
将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
m
假设结论不成立,从假设出发,得出矛盾.
反正法:
猜想:空间中过一点垂直于已知平面的直线有且只有一条.
反证法:假设过点P有两条直线a,b垂直于同一平面α.
设两直线确定的平面为β,且α∩β=c,所以c β.
由线面垂直的定义,知a⊥c,b⊥c,矛盾.
所以假设不成立,原命题成立.
已知:P是空间一点,直线a过点P,且a⊥α.
求证:a是唯一存在的.
问题3:在同一平面内,过一点有且只有一条直线与已知直线垂直.
将这一结论推广到空间,过一点垂直于已知平面的直线有几条?
结论2:过一点垂直于已知平面的直线有且只有一条.
垂线段:PA
点P到平面的距离:PA的长度
如:棱锥的高就是棱锥
的顶点到底面的距离.
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
问题4:用定义来判断线面垂直方便吗?
无限证明
有限证明
转化
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
追问1:一条直线至少与平面内的几条直线垂直,
才能够判定直线与平面垂直?
一条
线面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,
则直线l与平面α互相垂直.
追问1:一条直线至少与平面内的几条直线垂直,
才能够判定直线与平面垂直?
两条
探究:如图8.6-10,准备一块三角形的纸片ABC,过 ABC 的顶点A翻折纸片,
得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).
请你动手操作并思考:
(1)折痕AD与桌面垂直吗
(2)如何翻折才能使折痕AD与桌面垂直?
探究:如图8.6-10,准备一块三角形的纸片ABC,过 ABC 的顶点A翻折纸片,
得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).
请你动手操作并思考:
(1)折痕AD与桌面垂直吗
(2)如何翻折才能使折痕AD与桌面垂直?
猜想:当折痕AD⊥BC且翻折后BD与CD不在一条直线上时,
折痕AD与桌面所在的平面垂直.
追问2:如何验证折痕AD与桌面垂直?
A
B
D
C
m
探究成果:一条直线与平面内的两条相交直线垂直,
则直线与该平面垂直.
2.线面垂直的判定定理:一条直线与平面内的两条相交直线垂直,
那么直线与该平面垂直.
②符号语言:
①图形语言:
③本质:线线垂直→线面垂直
关键: 证两个线线垂直
m
n
P
问题5:两平行线中的一条垂直于平面,另一条是否也垂直于平面?
符号语言:
m
n
线线平行
线面垂直
传递
平行性质
例1
面面平行
线面垂直
传递
平行性质
变式 如图
1.直线与平面垂直
定义
判定定理
平行性质
证明方法
2.思想方法
(类比、化归)
线线垂直
线面垂直
转化
无限证明
有限证明
转化
文字语言
图形语言
转化
符号语言
转化
平行关系
垂直关系
转化
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
