8.6.2 直线与平面垂直 课件(共17张PPT)
文档属性
| 名称 | 8.6.2 直线与平面垂直 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 15:11:58 | ||
图片预览



文档简介
(共17张PPT)
8.6.2 直线与平面垂直
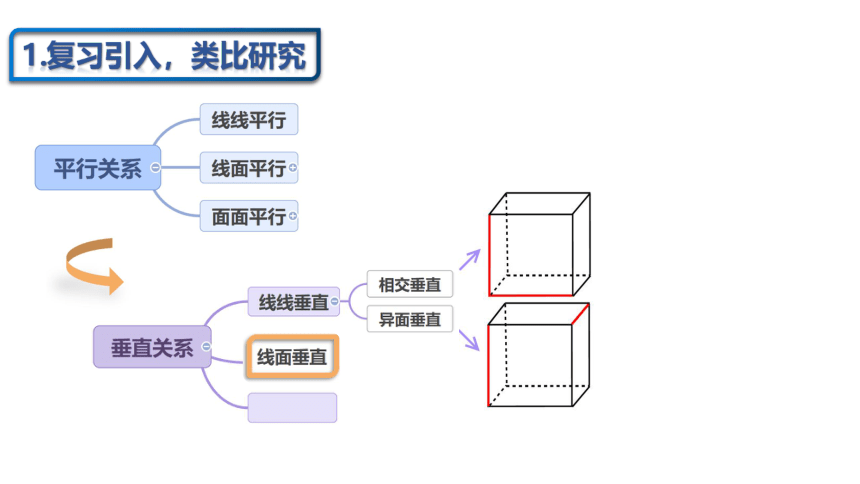
1.复习引入,类比研究
2.直观感知,归纳定义
问题1:在生活中,有哪些实例给我们直线与平面垂直的直观感受呢
比如:
旗杆垂直于地面
铅笔垂直于桌面
晷针垂直于晷面
数学化的定义?
直观感知
2.直观感知,归纳定义
问题2:结合旗杆例子进行探究,尝试得出线面垂直的数学化定义.
α
记作:l⊥α
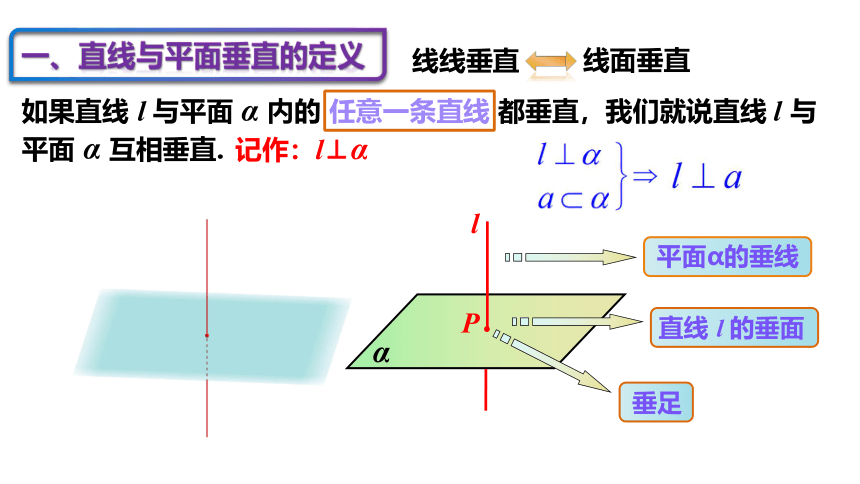
如果直线 l 与平面 α 内的 任意一条直线 都垂直,我们就说直线 l 与平面 α 互相垂直.
一、直线与平面垂直的定义
l
P
.
平面α的垂线
直线 l 的垂面
垂足
线线垂直
线面垂直
问:过一点作垂直于已知平面的直线有几条?
有且只有一条
α
P
.
O
.
l
垂线段
点到平面的距离
P
A
B
C
O
.
一、直线与平面垂直的定义
“点面距”
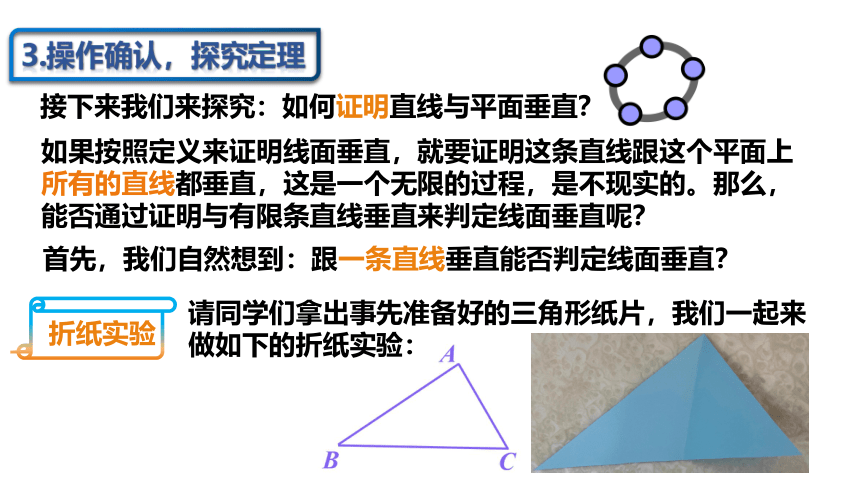
接下来我们来探究:如何证明直线与平面垂直?
如果按照定义来证明线面垂直,就要证明这条直线跟这个平面上所有的直线都垂直,这是一个无限的过程,是不现实的。那么,能否通过证明与有限条直线垂直来判定线面垂直呢?
首先,我们自然想到:跟一条直线垂直能否判定线面垂直?
3.操作确认,探究定理
请同学们拿出事先准备好的三角形纸片,我们一起来做如下的折纸实验:
折纸实验
当且仅当 折痕 AD 是 BC 边上的高时,AD 所在直线与桌面所在平面垂直.
3.操作确认,探究定理
一条直线与一个平面内的 两条相交直线 都垂直,则该直线与此平面垂直.
文字语言:
二、直线与平面垂直的判定定理
图形语言:
符号语言:
线线垂直
线面垂直
4.概念辨析,巩固新知
思考:
(1)如果一条直线与一个平面内的 两条直线 垂直,那么这条直线与平面垂直吗?
线不在多,
相交则灵
α
l
P
.
…
两条相交直线
(2)如果一条直线与一个平面内的 无数条直线 都垂直,那么这条直线与平面垂直吗?
任意一条直线
所有直线
小结:证明线面垂直的方法:
1.定义:
2.判定定理:
4.概念辨析,巩固新知
线线垂直
线面垂直
无限
有限
线不在多,
相交则灵
两条相交直线
所有直线
任意一条直线
5.推理论证,定理应用
例1 求证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
符号语言:
证明:
你能用直线与平面垂直的定义证明这个结论吗?
已知
求证:
在平面 α 内取两条相交直线 m,n,设m ∩ n=P.
∵ 直线 a⊥α,
∴ a⊥m,a⊥n
∵ b // a,
∴ b⊥m,b⊥n .
又 m ∩ n=P,
∴ b⊥α .
线线垂直 线面垂直
线面垂直 线线垂直
5.推理论证,定理应用
S
A
B
C
证明:
练习
如图,在三棱锥 S-ABC 中,∠ACB = 90°, SA⊥平面ABC .
求证:BC⊥平面SAC .
6.渗透文化,拓展延申
刘徽,是魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。
堑堵、阳马和鳖臑 等这些名词出自《九章算术商功》,而刘徽注道“斜解立方,得两堑堵。斜解堑堵,其一为阳马,一为鳖臑。阳马居二,鳖臑居一,不易之率也。”今称为刘徽原理。
刘徽
约225年—约295年
7.课堂小结,课后思考
3.判定定理的
简单应用
4.数学文化
的渗透
1.线面垂直
的定义
2.线面垂直的
判定定理
课堂小结
1.如果要检验一根新旗杆与地面是否垂直,你有什么好方法吗?
2.我们通过直观感知和操作确认,已经从直观上得出了线面垂直的判定定理,你能从理论上用所学的知识解释它吗?
7.课堂小结,课后思考
谢谢观看,再见!
8.6.2 直线与平面垂直
1.复习引入,类比研究
2.直观感知,归纳定义
问题1:在生活中,有哪些实例给我们直线与平面垂直的直观感受呢
比如:
旗杆垂直于地面
铅笔垂直于桌面
晷针垂直于晷面
数学化的定义?
直观感知
2.直观感知,归纳定义
问题2:结合旗杆例子进行探究,尝试得出线面垂直的数学化定义.
α
记作:l⊥α
如果直线 l 与平面 α 内的 任意一条直线 都垂直,我们就说直线 l 与平面 α 互相垂直.
一、直线与平面垂直的定义
l
P
.
平面α的垂线
直线 l 的垂面
垂足
线线垂直
线面垂直
问:过一点作垂直于已知平面的直线有几条?
有且只有一条
α
P
.
O
.
l
垂线段
点到平面的距离
P
A
B
C
O
.
一、直线与平面垂直的定义
“点面距”
接下来我们来探究:如何证明直线与平面垂直?
如果按照定义来证明线面垂直,就要证明这条直线跟这个平面上所有的直线都垂直,这是一个无限的过程,是不现实的。那么,能否通过证明与有限条直线垂直来判定线面垂直呢?
首先,我们自然想到:跟一条直线垂直能否判定线面垂直?
3.操作确认,探究定理
请同学们拿出事先准备好的三角形纸片,我们一起来做如下的折纸实验:
折纸实验
当且仅当 折痕 AD 是 BC 边上的高时,AD 所在直线与桌面所在平面垂直.
3.操作确认,探究定理
一条直线与一个平面内的 两条相交直线 都垂直,则该直线与此平面垂直.
文字语言:
二、直线与平面垂直的判定定理
图形语言:
符号语言:
线线垂直
线面垂直
4.概念辨析,巩固新知
思考:
(1)如果一条直线与一个平面内的 两条直线 垂直,那么这条直线与平面垂直吗?
线不在多,
相交则灵
α
l
P
.
…
两条相交直线
(2)如果一条直线与一个平面内的 无数条直线 都垂直,那么这条直线与平面垂直吗?
任意一条直线
所有直线
小结:证明线面垂直的方法:
1.定义:
2.判定定理:
4.概念辨析,巩固新知
线线垂直
线面垂直
无限
有限
线不在多,
相交则灵
两条相交直线
所有直线
任意一条直线
5.推理论证,定理应用
例1 求证:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
符号语言:
证明:
你能用直线与平面垂直的定义证明这个结论吗?
已知
求证:
在平面 α 内取两条相交直线 m,n,设m ∩ n=P.
∵ 直线 a⊥α,
∴ a⊥m,a⊥n
∵ b // a,
∴ b⊥m,b⊥n .
又 m ∩ n=P,
∴ b⊥α .
线线垂直 线面垂直
线面垂直 线线垂直
5.推理论证,定理应用
S
A
B
C
证明:
练习
如图,在三棱锥 S-ABC 中,∠ACB = 90°, SA⊥平面ABC .
求证:BC⊥平面SAC .
6.渗透文化,拓展延申
刘徽,是魏晋期间伟大的数学家,中国古典数学理论的奠基人之一。
堑堵、阳马和鳖臑 等这些名词出自《九章算术商功》,而刘徽注道“斜解立方,得两堑堵。斜解堑堵,其一为阳马,一为鳖臑。阳马居二,鳖臑居一,不易之率也。”今称为刘徽原理。
刘徽
约225年—约295年
7.课堂小结,课后思考
3.判定定理的
简单应用
4.数学文化
的渗透
1.线面垂直
的定义
2.线面垂直的
判定定理
课堂小结
1.如果要检验一根新旗杆与地面是否垂直,你有什么好方法吗?
2.我们通过直观感知和操作确认,已经从直观上得出了线面垂直的判定定理,你能从理论上用所学的知识解释它吗?
7.课堂小结,课后思考
谢谢观看,再见!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
