9.1.1 简单随机抽样 课件(共26张PPT)
文档属性
| 名称 | 9.1.1 简单随机抽样 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 598.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 15:12:52 | ||
图片预览








文档简介
(共26张PPT)
9.1.1简单随机抽样
中国仍旧是人口第一大国家
浙江卫视《奔跑吧》电视收视率:3.263%
1. 你知道这些数据是如何获取的?
2. 要了解一箱苹果是否碰撞腐烂,如何调查?
3. 要知晓一箱酸奶是否新鲜,需要逐一检查吗?
调查
逐个检查,即全面调查
具有破坏性,不能全面调查,采用抽样调查
想一想:
基本概念
全面调查
像人口普查这样,对每一个调查对象都进行调查的方法,称为全面调查,又称普查。.
根据一定目的,从总体中抽取一部分个体进行调查,
并以此为依据对总体的情况作出估计和推断的调查
方法,称为抽样调查
抽样调查
调查对象的全体称为总体,组成总体的每一个调查对象称为个体。
从总体中抽取的那部分个体称为样本,样本中包含的个体数称为样本容量,简称样本量。
生活中更多的是抽样调查,比如:一批灯泡的寿命,一批种子的发芽率等等。
统计的基本思想方法就是用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的情况.
思考:如何抽样才能抽取到一个“好”的样本呢?
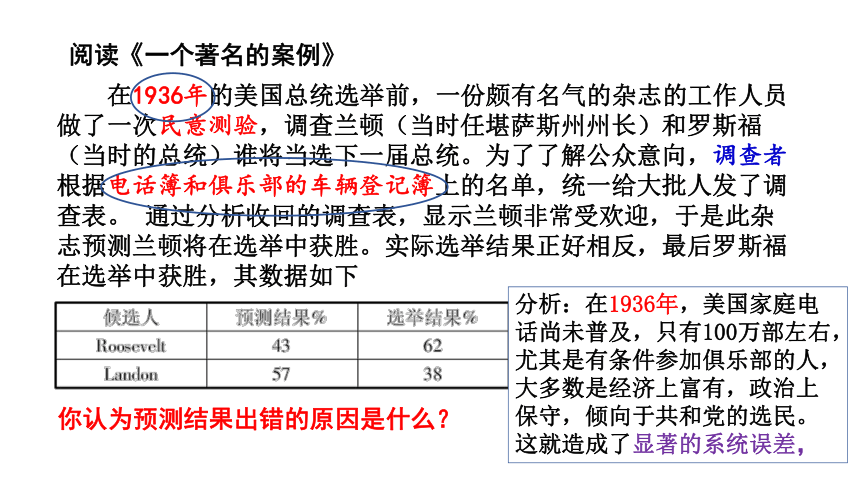
在1936年的美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意测验,调查兰顿(当时任堪萨斯州州长)和罗斯福(当时的总统)谁将当选下一届总统。为了了解公众意向,调查者根据电话簿和俱乐部的车辆登记簿上的名单,统一给大批人发了调查表。 通过分析收回的调查表,显示兰顿非常受欢迎,于是此杂志预测兰顿将在选举中获胜。实际选举结果正好相反,最后罗斯福在选举中获胜,其数据如下
阅读《一个著名的案例》
你认为预测结果出错的原因是什么?
或许都来自堪萨斯州?
分析:在1936年,美国家庭电话尚未普及,只有100万部左右,尤其是有条件参加俱乐部的人,大多数是经济上富有,政治上保守,倾向于共和党的选民。这就造成了显著的系统误差,
想知道一锅汤的味道,需要把整锅汤都都喝掉吗?应该如何判断?
不需要,只要将锅里的汤搅拌均匀,品尝一勺就知道汤的味道.
抽样时要搅拌均匀,让每一个个体都可能被抽到,并且每一个个体被抽到的机会是均等的。
生活中的数学
假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同,你能通过抽样调查的方法估计袋中红球所占的比例吗?
现有两种方案:
方案1:从袋中随机地摸出一个球,记录颜色后放回,摇匀后再摸出一个球,如此重复n次;
方案2:从袋中随机地摸出一个球,记录颜色后不再放回袋中,每次摸球都在余下的球中随机摸取,如此n次。
请同学们分组讨论:以上两种方案能否估计出红球的比例,请说明理由,并比较两种方案的优劣?
优缺点:
①放回摸球的缺点:同一小球可能被重复摸中,极端情况可能一直被摸到。
②不放回摸球的优点:避免同一个小球被重复摸中,并且当样本量n=1000时,完全了解红球比例。
两种方案都可行,根据初中的概率知识,随着次数增加,摸到红球的频率逐渐稳定于概率,(即口袋中红球所占的比例)。
疑 问?
你认为这样的认识对吗?为什么?
两种方案在同样的条件下,执行过程中可能性似乎并不相等。比如:从含有10个个体的总体中,抽取容量为3的样本。其中个体甲在第二次被抽到的可能性就不相同,采用放回抽样方案,可能性是 ;采用不放回抽样方案,其可能性是 。
在可放回抽样中,每个个体在每次抽取时被抽到的可
能性均为 ,与第几次无关,所以答案是 .
在不可放回抽样中,甲在第一次未被抽到 ,甲在
第二次抽到 ,故甲在第二次被抽到的可能性为
。
甲在第三次被抽到的可能性是多少?
不放回抽样的过程中,某一个个体不论是它被第几次抽到,被抽的可能性都是相等;与放回抽样的可能性相等。
简单随机抽样
放回简单随机抽样
不放回简单随机抽样
抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等。
抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等。
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤ n<N)个个体作为样本。
放回简单随机抽样和不放回简单随机抽样统称为简单随机抽样。
不放回抽取的效率更高,一般默认简单随机抽样为不放回的。
逐个不放回随机抽取n个等价于一次性批量随机抽取n个。
想一想:简单随机抽样有哪些特点?
(1)有限性:总体的个数是有限;
(2)逐一性:样本的抽取是逐一进行的,每次只抽取 一个个体;
(3)等可能性:每个个体被抽到的机会都相等,抽样具有公平性.
例1 判断下列抽样的方式是否属于简单随机抽样?
(1)从无限多个个体中抽取100个个体作为样本.
(2)某班45名同学,指定个子最高的5名同学参加学校组织的某项活动
(3)从20件玩具中一次性抽取3件进行质量检查.
×
√
×
(1)错误:总体的个数是无限的,
(2)每个个体被抽到的可能性不同;
现要在我们班45位同学中选派5个人去参加某项户外活动,为了体现选派的公平性,你有什么办法确定具体人选
实 例 一
抽签决定
如何具体实施?
1.编号:给总体中所有的个体编号
2.制签:将1 ~ N这N个号码写在相同的号签上
5.取样:从总体中,将与抽到的号签编号一致的个体取出
4.抽签:每次从容器中不放回地抽取一个号签,并记录其编号,连续抽取n次
3.搅拌:将号签放在一个不透明的容器中,搅拌均匀
抽签法的一般步骤:
一家家具厂要为树人中学高一年级制作课座椅,他们事先想了解全体高一年级学生的平均身高,以便设定可调节座椅的标准高度。已知树人中学高一年级有712名学生,从中抽取150名学生进行测量身高,若用抽签法抽取,请说其过程。
实 例 二
编号-给712名学生编号;
制签-将1-712个号码写在相同的号签上;
搅拌-将号签放在一个不透明的容器中,搅拌均匀;
抽签-从容器中不放回地逐个抽取150次;
取样-从712名学生中选出与号签编号相同的学生。
思考:抽签法有什么优缺点?当总体中个体数很多时,此法方便吗?
优点:简单易行,每个个体有均等的机会被抽中,能保证样本的代表性.
缺点:(1)总体容量大时,制作号签的成本会增加费时、费力.
(2)号签很多, “搅拌均匀”困难,产生的样本的代表性差的可能性大.
有简化制签的方法吗?
随机数法
1.编号:给总体中所有的个体编号
2.选号:用随机数工具产生编号范围内的整数随机数,把产生的随机数作为抽中的编号,使与编号对应的个体进入样本.重复上述过程,直到抽足样本所需要的个体数,如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号,并重新产生随机数,直到产生的不同编号个数等于样本所需要的个体数
3.取样:把选定的号码对应的n个个体作为样本
随机数法的一般步骤:
(1)随机试验生成随机数
①准备十个大小、质地一样的小球,小球上面分别写0,1,2,···,9,把它们放到一个不透明的袋中。
②有放回地摸取3次,每次摸取前充分搅拌;
③把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成了一个三位数。
④如果这个三位数在范围内,则抽中对应编号的学生,否则舍弃,重复的数剔除。
生成随机数的方法
1.用计算器生成随机数
生成随机数的函数为
RandInt#(1,712)
2.用电子表格软件生成随机数
=RANDBETWEEN(1,712)
3.用R统计软件生成随机数
=sample(1:712,50,replace=F)
(2)用信息技术生成随机数
思考:试比较抽签法与随机数法的优缺点?
抽样方法 优点 缺点 适用范围
抽签法 简单易行 总体量较大时,操作起来较麻烦 适用于总体中个体数不多的情形
随机数法 简单易行,很好地解决了总体量较大时用抽签法制签困难的问题。 总体量较大,样本量也很大时,利用随机数法抽取样本仍然不方便 适用于总体量大、样本量较小的情形
用简单随机抽样方法抽取样本,样本量是否越大越好?
在重复试验中,试验次数越多,频率接近于概率的可能性越大,于是,样本量越大,效果越好;但是,在实际抽样中,样本量的增大会导致调查的人力、费用、时间等成本的增加,因此,抽样调查中的样本量的选择根据实际的需要,不一定越大越好。
课堂小结
1.两种调查方式:
2.理解简单随机抽样的概念
3.实现简单随机抽样的方法:
9.1.1简单随机抽样
中国仍旧是人口第一大国家
浙江卫视《奔跑吧》电视收视率:3.263%
1. 你知道这些数据是如何获取的?
2. 要了解一箱苹果是否碰撞腐烂,如何调查?
3. 要知晓一箱酸奶是否新鲜,需要逐一检查吗?
调查
逐个检查,即全面调查
具有破坏性,不能全面调查,采用抽样调查
想一想:
基本概念
全面调查
像人口普查这样,对每一个调查对象都进行调查的方法,称为全面调查,又称普查。.
根据一定目的,从总体中抽取一部分个体进行调查,
并以此为依据对总体的情况作出估计和推断的调查
方法,称为抽样调查
抽样调查
调查对象的全体称为总体,组成总体的每一个调查对象称为个体。
从总体中抽取的那部分个体称为样本,样本中包含的个体数称为样本容量,简称样本量。
生活中更多的是抽样调查,比如:一批灯泡的寿命,一批种子的发芽率等等。
统计的基本思想方法就是用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的情况.
思考:如何抽样才能抽取到一个“好”的样本呢?
在1936年的美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意测验,调查兰顿(当时任堪萨斯州州长)和罗斯福(当时的总统)谁将当选下一届总统。为了了解公众意向,调查者根据电话簿和俱乐部的车辆登记簿上的名单,统一给大批人发了调查表。 通过分析收回的调查表,显示兰顿非常受欢迎,于是此杂志预测兰顿将在选举中获胜。实际选举结果正好相反,最后罗斯福在选举中获胜,其数据如下
阅读《一个著名的案例》
你认为预测结果出错的原因是什么?
或许都来自堪萨斯州?
分析:在1936年,美国家庭电话尚未普及,只有100万部左右,尤其是有条件参加俱乐部的人,大多数是经济上富有,政治上保守,倾向于共和党的选民。这就造成了显著的系统误差,
想知道一锅汤的味道,需要把整锅汤都都喝掉吗?应该如何判断?
不需要,只要将锅里的汤搅拌均匀,品尝一勺就知道汤的味道.
抽样时要搅拌均匀,让每一个个体都可能被抽到,并且每一个个体被抽到的机会是均等的。
生活中的数学
假设口袋中有红色和白色共1000个小球,除颜色外,小球的大小、质地完全相同,你能通过抽样调查的方法估计袋中红球所占的比例吗?
现有两种方案:
方案1:从袋中随机地摸出一个球,记录颜色后放回,摇匀后再摸出一个球,如此重复n次;
方案2:从袋中随机地摸出一个球,记录颜色后不再放回袋中,每次摸球都在余下的球中随机摸取,如此n次。
请同学们分组讨论:以上两种方案能否估计出红球的比例,请说明理由,并比较两种方案的优劣?
优缺点:
①放回摸球的缺点:同一小球可能被重复摸中,极端情况可能一直被摸到。
②不放回摸球的优点:避免同一个小球被重复摸中,并且当样本量n=1000时,完全了解红球比例。
两种方案都可行,根据初中的概率知识,随着次数增加,摸到红球的频率逐渐稳定于概率,(即口袋中红球所占的比例)。
疑 问?
你认为这样的认识对吗?为什么?
两种方案在同样的条件下,执行过程中可能性似乎并不相等。比如:从含有10个个体的总体中,抽取容量为3的样本。其中个体甲在第二次被抽到的可能性就不相同,采用放回抽样方案,可能性是 ;采用不放回抽样方案,其可能性是 。
在可放回抽样中,每个个体在每次抽取时被抽到的可
能性均为 ,与第几次无关,所以答案是 .
在不可放回抽样中,甲在第一次未被抽到 ,甲在
第二次抽到 ,故甲在第二次被抽到的可能性为
。
甲在第三次被抽到的可能性是多少?
不放回抽样的过程中,某一个个体不论是它被第几次抽到,被抽的可能性都是相等;与放回抽样的可能性相等。
简单随机抽样
放回简单随机抽样
不放回简单随机抽样
抽取是放回的,且每次抽取时总体内的各个个体被抽到的概率都相等。
抽取是不放回的,且每次抽取时总体内未进入样本的各个个体被抽到的概率都相等。
一般地,设一个总体含有N(N为正整数)个个体,从中逐个抽取n(1≤ n<N)个个体作为样本。
放回简单随机抽样和不放回简单随机抽样统称为简单随机抽样。
不放回抽取的效率更高,一般默认简单随机抽样为不放回的。
逐个不放回随机抽取n个等价于一次性批量随机抽取n个。
想一想:简单随机抽样有哪些特点?
(1)有限性:总体的个数是有限;
(2)逐一性:样本的抽取是逐一进行的,每次只抽取 一个个体;
(3)等可能性:每个个体被抽到的机会都相等,抽样具有公平性.
例1 判断下列抽样的方式是否属于简单随机抽样?
(1)从无限多个个体中抽取100个个体作为样本.
(2)某班45名同学,指定个子最高的5名同学参加学校组织的某项活动
(3)从20件玩具中一次性抽取3件进行质量检查.
×
√
×
(1)错误:总体的个数是无限的,
(2)每个个体被抽到的可能性不同;
现要在我们班45位同学中选派5个人去参加某项户外活动,为了体现选派的公平性,你有什么办法确定具体人选
实 例 一
抽签决定
如何具体实施?
1.编号:给总体中所有的个体编号
2.制签:将1 ~ N这N个号码写在相同的号签上
5.取样:从总体中,将与抽到的号签编号一致的个体取出
4.抽签:每次从容器中不放回地抽取一个号签,并记录其编号,连续抽取n次
3.搅拌:将号签放在一个不透明的容器中,搅拌均匀
抽签法的一般步骤:
一家家具厂要为树人中学高一年级制作课座椅,他们事先想了解全体高一年级学生的平均身高,以便设定可调节座椅的标准高度。已知树人中学高一年级有712名学生,从中抽取150名学生进行测量身高,若用抽签法抽取,请说其过程。
实 例 二
编号-给712名学生编号;
制签-将1-712个号码写在相同的号签上;
搅拌-将号签放在一个不透明的容器中,搅拌均匀;
抽签-从容器中不放回地逐个抽取150次;
取样-从712名学生中选出与号签编号相同的学生。
思考:抽签法有什么优缺点?当总体中个体数很多时,此法方便吗?
优点:简单易行,每个个体有均等的机会被抽中,能保证样本的代表性.
缺点:(1)总体容量大时,制作号签的成本会增加费时、费力.
(2)号签很多, “搅拌均匀”困难,产生的样本的代表性差的可能性大.
有简化制签的方法吗?
随机数法
1.编号:给总体中所有的个体编号
2.选号:用随机数工具产生编号范围内的整数随机数,把产生的随机数作为抽中的编号,使与编号对应的个体进入样本.重复上述过程,直到抽足样本所需要的个体数,如果生成的随机数有重复,即同一编号被多次抽到,可以剔除重复的编号,并重新产生随机数,直到产生的不同编号个数等于样本所需要的个体数
3.取样:把选定的号码对应的n个个体作为样本
随机数法的一般步骤:
(1)随机试验生成随机数
①准备十个大小、质地一样的小球,小球上面分别写0,1,2,···,9,把它们放到一个不透明的袋中。
②有放回地摸取3次,每次摸取前充分搅拌;
③把第一、二、三次摸到的数字分别作为百、十、个位数,这样就生成了一个三位数。
④如果这个三位数在范围内,则抽中对应编号的学生,否则舍弃,重复的数剔除。
生成随机数的方法
1.用计算器生成随机数
生成随机数的函数为
RandInt#(1,712)
2.用电子表格软件生成随机数
=RANDBETWEEN(1,712)
3.用R统计软件生成随机数
=sample(1:712,50,replace=F)
(2)用信息技术生成随机数
思考:试比较抽签法与随机数法的优缺点?
抽样方法 优点 缺点 适用范围
抽签法 简单易行 总体量较大时,操作起来较麻烦 适用于总体中个体数不多的情形
随机数法 简单易行,很好地解决了总体量较大时用抽签法制签困难的问题。 总体量较大,样本量也很大时,利用随机数法抽取样本仍然不方便 适用于总体量大、样本量较小的情形
用简单随机抽样方法抽取样本,样本量是否越大越好?
在重复试验中,试验次数越多,频率接近于概率的可能性越大,于是,样本量越大,效果越好;但是,在实际抽样中,样本量的增大会导致调查的人力、费用、时间等成本的增加,因此,抽样调查中的样本量的选择根据实际的需要,不一定越大越好。
课堂小结
1.两种调查方式:
2.理解简单随机抽样的概念
3.实现简单随机抽样的方法:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
