三、走进数字电路 课件(31张PPT)
文档属性
| 名称 | 三、走进数字电路 课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 通用技术 | ||
| 更新时间 | 2024-04-28 13:42:29 | ||
图片预览

文档简介
(共31张PPT)
走进数字电路
甲、乙、丙三人参加表决 表决规则:少数服从多数
通过—绿灯亮;不通过—红灯亮
处理
电路
甲
乙
丙
红灯
绿灯
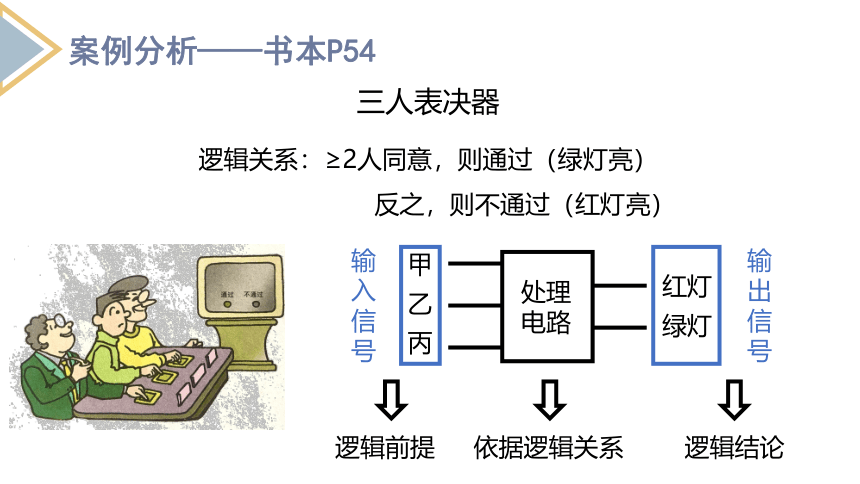
逻辑关系:≥2人同意,则通过(绿灯亮)
反之,则不通过(红灯亮)
输入信号
输出信号
三人表决器
逻辑前提
逻辑结论
依据逻辑关系
案例分析——书本P54
案例分析——书本P54
处理
电路
甲
乙
丙
红灯
绿灯
逻辑前提
逻辑结论
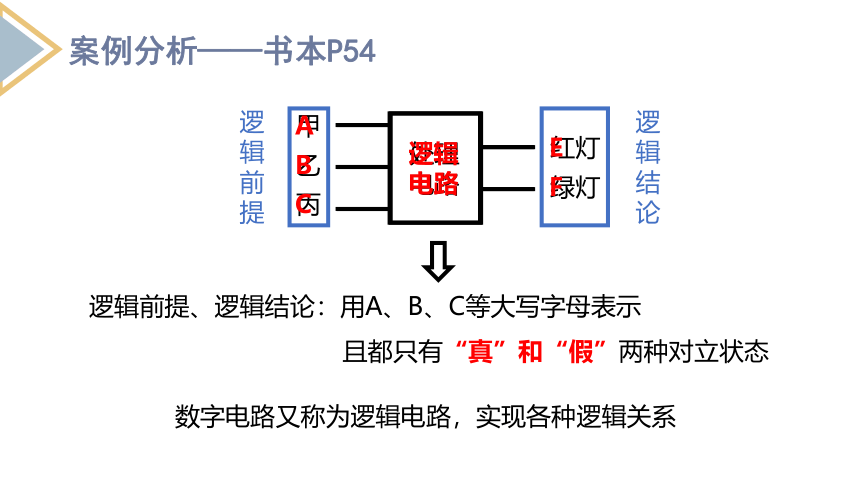
逻辑前提、逻辑结论:用A、B、C等大写字母表示
且都只有“真”和“假”两种对立状态
数字电路又称为逻辑电路,实现各种逻辑关系
逻辑电路
A
B
C
E
F
三种基本逻辑门
门电路:数字电路最基本的单元
三种基本逻辑门:
与门(AND)、或门(OR)、非门(NOT)
与门(AND)
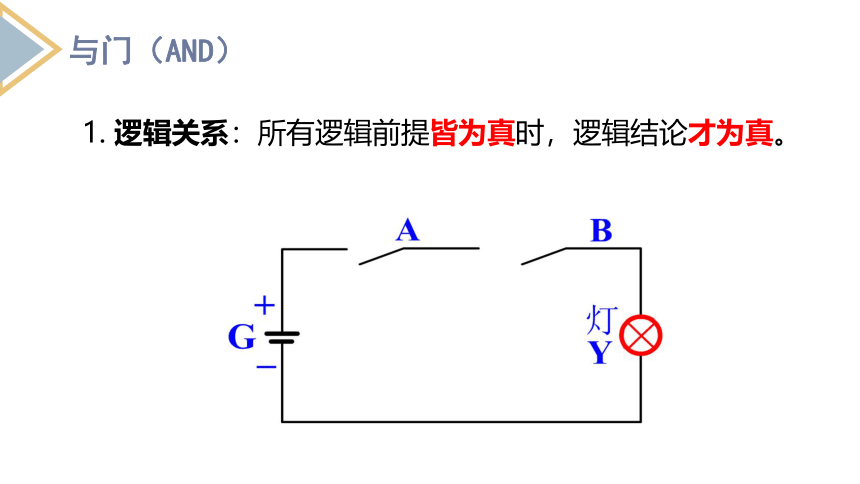
1. 逻辑关系:所有逻辑前提皆为真时,逻辑结论才为真。
A B Y
假 假 假
假 真 假
真 假 假
真 真 真
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
A B Y
假 假 假
假 真 假
真 假 假
真 真 真
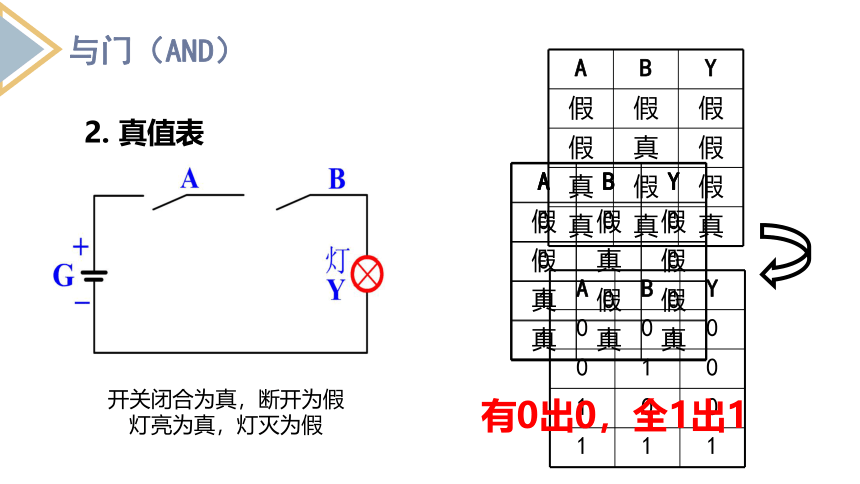
开关闭合为真,断开为假
灯亮为真,灯灭为假
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
有0出0,全1出1
2. 真值表
与门(AND)
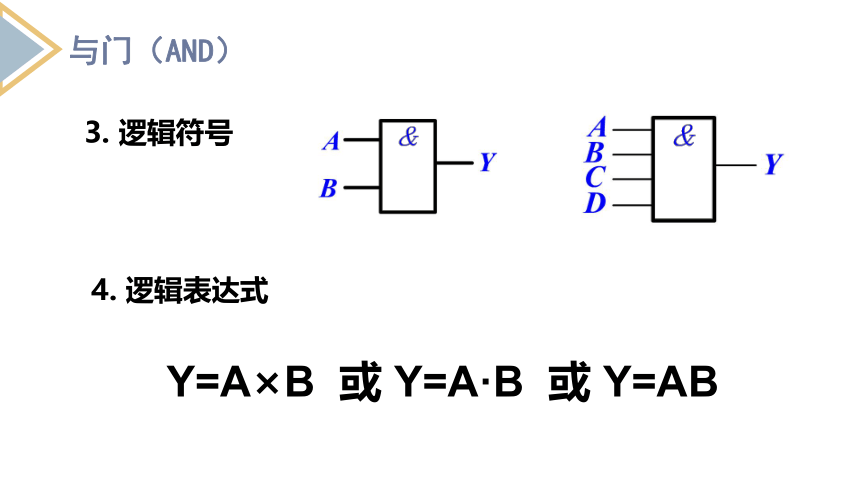
3. 逻辑符号
4. 逻辑表达式
Y=A×B 或 Y=A·B 或 Y=AB
与门(AND)
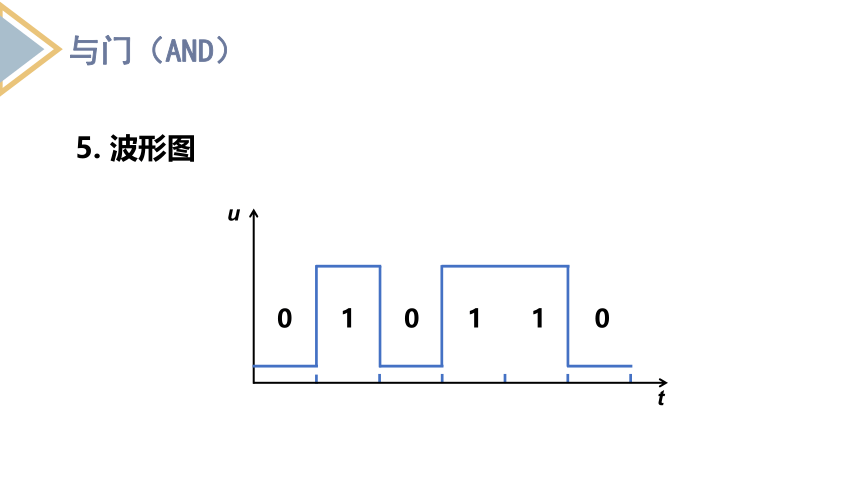
5. 波形图
0
1
0
1
1
0
与门(AND)
u
t
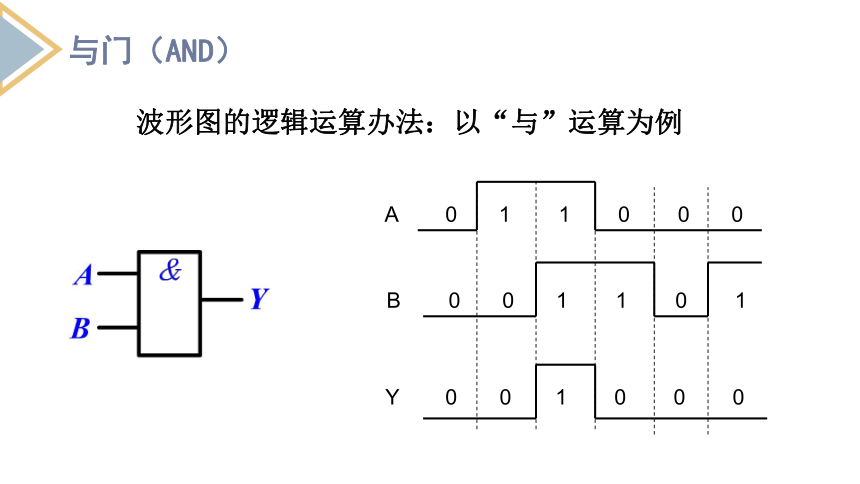
A 0 1 1 0 0 0
B 0 0 1 1 0 1
Y
波形图的逻辑运算办法:以“与”运算为例
0
0
1
0
0
0
与门(AND)
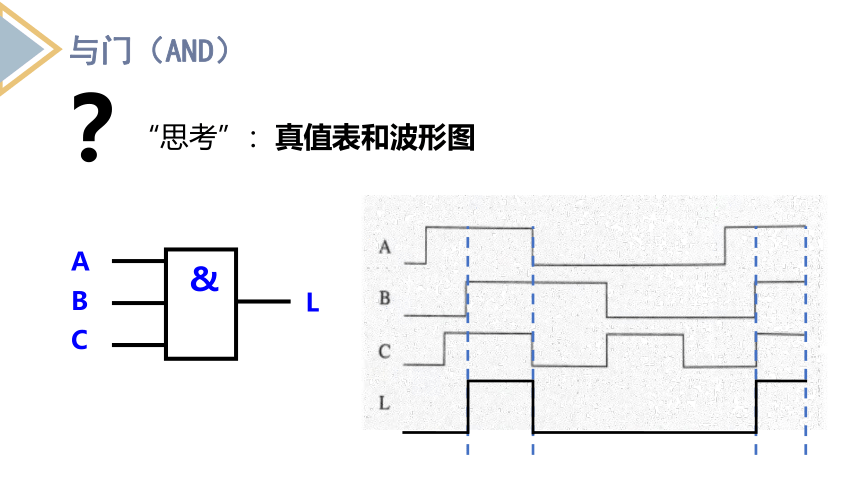
“思考”:真值表和波形图
?
&
A
B
C
L
与门(AND)
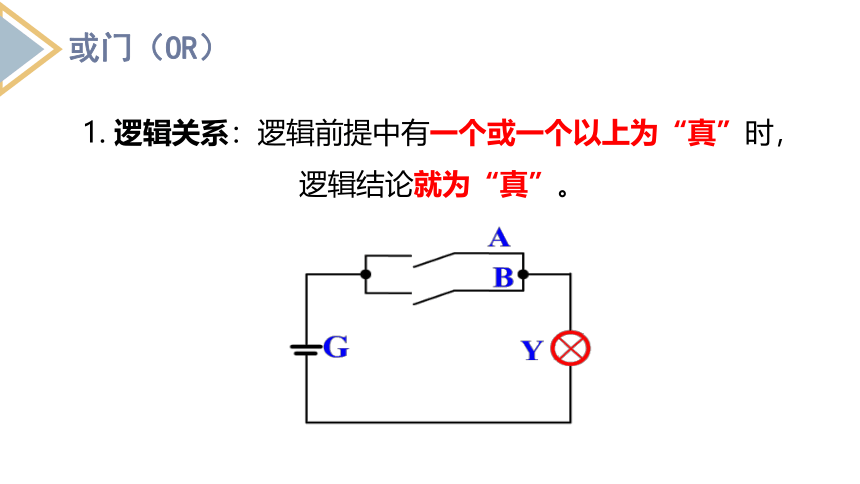
或门(OR)
1. 逻辑关系:逻辑前提中有一个或一个以上为“真”时,逻辑结论就为“真”。
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
A B Y
假 假 假
假 真 真
真 假 真
真 真 真
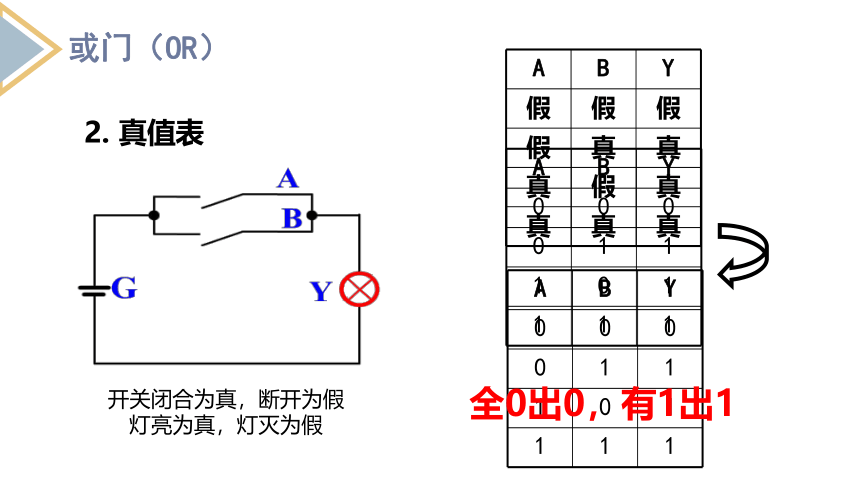
开关闭合为真,断开为假
灯亮为真,灯灭为假
全0出0,有1出1
2. 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
或门(OR)
3. 逻辑符号
4. 逻辑表达式
Y=A+B
或门(OR)
A 0 1 1 0 0 0
B 0 0 1 1 0 1
Y
0
1
1
1
0
1
注:逻辑运算没有进位,也就是说1+1=1。
或门(OR)
5. 波形图
“思考”:真值表和波形图
?
≥1
A
B
C
L
或门(OR)
非门(NOT)
1. 逻辑关系:逻辑前提为假时逻辑结论为真
逻辑前提为真时逻辑结论为假
2. 真值表
A Y
0 1
1 0
3. 逻辑符号
4. 逻辑表达式
Y= A
非门(NOT)
三人表决器的电路设计方法
绿灯亮的条件是:AB同意或AC同意或BC同意或ABC都同意
逻辑电路
A
B
C
Y1
Y2
利用逻辑代数化简得到:Y1=AB+AC+BC
红灯亮的条件是:Y2=Y1
逻辑代数:Y1=AB+ AC+ BC+ABC
三人表决器的电路设计方法
组合逻辑门
由三种基本逻辑关系推演可得
两种复杂逻辑关系:“与非”、“或非”
组合逻辑门:
与非门(NAND)、或非门(NOR)
与非门(NAND)
1. 逻辑符号
2. 逻辑表达式
Y=A×B 或 Y= A·B 或 Y= AB
3. 真值表
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
有0出1,全1出0
1
1
1
0
与门
与非门
与非门(NAND)
或非门(NOR)
1. 逻辑符号
2. 逻辑表达式
Y= A+B
3. 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
全0出1,有1出0
1
0
0
0
或门
或非门
或非门(NOR)
常见数字集成电路的类型
参数名称 TTL CMOS
结构 普通晶体三极管 MOS管
电源电压 5V 3~18V
高电平(标称值) 3V VDD
低电平(标称值) 0.3V 0V
门平均功耗 2~22mW 50nW
最高工作频率 35~125MHz 25MHz
最大输出电流 20~100mA 3.5mA
多余引脚 与门/与非门:接高电平(电源) 或门/或非门:接低电平(地)
常见数字集成电路的类型
常用集成与非门:
CT74LS00、CT4LS20、CC4011、CC4012等
常用集成或非门:
CT74LS02、CC4001、CC4002等
常用集成逻辑门电路的命名
如:四 2 输入与非门
内部有4个门
每个门有2个输入端
常见数字集成电路引脚编排顺序
计数方向
常见集成与非门的结构区别
门电路的逻辑关系
总结
与门:“全高出高,见低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
与非门:“全高出低,见低出高”
或非门:“见高出低,全低出高”
谢谢观看
走进数字电路
甲、乙、丙三人参加表决 表决规则:少数服从多数
通过—绿灯亮;不通过—红灯亮
处理
电路
甲
乙
丙
红灯
绿灯
逻辑关系:≥2人同意,则通过(绿灯亮)
反之,则不通过(红灯亮)
输入信号
输出信号
三人表决器
逻辑前提
逻辑结论
依据逻辑关系
案例分析——书本P54
案例分析——书本P54
处理
电路
甲
乙
丙
红灯
绿灯
逻辑前提
逻辑结论
逻辑前提、逻辑结论:用A、B、C等大写字母表示
且都只有“真”和“假”两种对立状态
数字电路又称为逻辑电路,实现各种逻辑关系
逻辑电路
A
B
C
E
F
三种基本逻辑门
门电路:数字电路最基本的单元
三种基本逻辑门:
与门(AND)、或门(OR)、非门(NOT)
与门(AND)
1. 逻辑关系:所有逻辑前提皆为真时,逻辑结论才为真。
A B Y
假 假 假
假 真 假
真 假 假
真 真 真
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
A B Y
假 假 假
假 真 假
真 假 假
真 真 真
开关闭合为真,断开为假
灯亮为真,灯灭为假
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
有0出0,全1出1
2. 真值表
与门(AND)
3. 逻辑符号
4. 逻辑表达式
Y=A×B 或 Y=A·B 或 Y=AB
与门(AND)
5. 波形图
0
1
0
1
1
0
与门(AND)
u
t
A 0 1 1 0 0 0
B 0 0 1 1 0 1
Y
波形图的逻辑运算办法:以“与”运算为例
0
0
1
0
0
0
与门(AND)
“思考”:真值表和波形图
?
&
A
B
C
L
与门(AND)
或门(OR)
1. 逻辑关系:逻辑前提中有一个或一个以上为“真”时,逻辑结论就为“真”。
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
A B Y
假 假 假
假 真 真
真 假 真
真 真 真
开关闭合为真,断开为假
灯亮为真,灯灭为假
全0出0,有1出1
2. 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
或门(OR)
3. 逻辑符号
4. 逻辑表达式
Y=A+B
或门(OR)
A 0 1 1 0 0 0
B 0 0 1 1 0 1
Y
0
1
1
1
0
1
注:逻辑运算没有进位,也就是说1+1=1。
或门(OR)
5. 波形图
“思考”:真值表和波形图
?
≥1
A
B
C
L
或门(OR)
非门(NOT)
1. 逻辑关系:逻辑前提为假时逻辑结论为真
逻辑前提为真时逻辑结论为假
2. 真值表
A Y
0 1
1 0
3. 逻辑符号
4. 逻辑表达式
Y= A
非门(NOT)
三人表决器的电路设计方法
绿灯亮的条件是:AB同意或AC同意或BC同意或ABC都同意
逻辑电路
A
B
C
Y1
Y2
利用逻辑代数化简得到:Y1=AB+AC+BC
红灯亮的条件是:Y2=Y1
逻辑代数:Y1=AB+ AC+ BC+ABC
三人表决器的电路设计方法
组合逻辑门
由三种基本逻辑关系推演可得
两种复杂逻辑关系:“与非”、“或非”
组合逻辑门:
与非门(NAND)、或非门(NOR)
与非门(NAND)
1. 逻辑符号
2. 逻辑表达式
Y=A×B 或 Y= A·B 或 Y= AB
3. 真值表
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
有0出1,全1出0
1
1
1
0
与门
与非门
与非门(NAND)
或非门(NOR)
1. 逻辑符号
2. 逻辑表达式
Y= A+B
3. 真值表
A B Y
0 0 0
0 1 1
1 0 1
1 1 1
全0出1,有1出0
1
0
0
0
或门
或非门
或非门(NOR)
常见数字集成电路的类型
参数名称 TTL CMOS
结构 普通晶体三极管 MOS管
电源电压 5V 3~18V
高电平(标称值) 3V VDD
低电平(标称值) 0.3V 0V
门平均功耗 2~22mW 50nW
最高工作频率 35~125MHz 25MHz
最大输出电流 20~100mA 3.5mA
多余引脚 与门/与非门:接高电平(电源) 或门/或非门:接低电平(地)
常见数字集成电路的类型
常用集成与非门:
CT74LS00、CT4LS20、CC4011、CC4012等
常用集成或非门:
CT74LS02、CC4001、CC4002等
常用集成逻辑门电路的命名
如:四 2 输入与非门
内部有4个门
每个门有2个输入端
常见数字集成电路引脚编排顺序
计数方向
常见集成与非门的结构区别
门电路的逻辑关系
总结
与门:“全高出高,见低出低”
或门:“见高出高,全低出低”
非门:“见高出低,见低出高”
与非门:“全高出低,见低出高”
或非门:“见高出低,全低出高”
谢谢观看
同课章节目录
