19.2.1 正比例函数课件(15张PPT) 2023-2024学年人教版数学年八年级下册
文档属性
| 名称 | 19.2.1 正比例函数课件(15张PPT) 2023-2024学年人教版数学年八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 295.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
正比例函数的概念
人教版·初中数学·八年级下册·第十九章
19.2.1 正比例函数
学
习
目
标
1.理解正比例函数的概念;
2.会求正比例函数的解析式;
3.能利用正比例函数解决简单的实际问题.
下列问题中的变量对应规律可用怎样的函数解析式表示?
(1)圆的周长l随半径r的大小变化而变化.
(2)市场上苹果每千克7.5元,买苹果所需的钱数y(单位:元)随购买的数量x(单位:千克)的变化而变化.
解:l=2πr
解:y =7.5 x .
问题探究
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随这些练习本的本数n的变化而变化.
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T
(单位:℃)随冷冻时间t(单位:分)的变化而变化.
解:h = 0.5n .
解:T=-2t.
问题探究
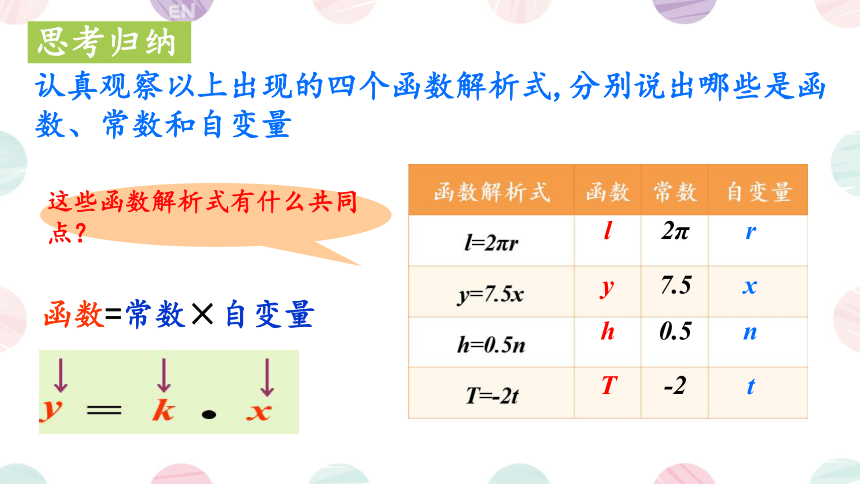
思考归纳
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量
函数=常数×自变量
这些函数解析式有什么共同点?
l
r
2π
y
7.5
x
T
-2
n
h
0.5
t
知识要点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比
例函数,其中k叫做比例系数.
正比例函数解析式的特点:
(1)k是常数,k≠0 ;
(3)函数关系式的左边是函数、右边是常量与自变量的乘积。
(2)变量x、y的指数都是1;
下列式子,哪些表示y是x的正比例函数 如果是,请你指出比例系数k的值.
概念辨析
√
√
√
√
变式巩固
2.若y=(n-1)x|n|是正比例函数,则n= .
-1
1.如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
4
-2
2
3.若 是正比例函数,则 m = .
4.若 是正比例函数,则 m = .
判断正比例函数:形式上要满足y=kx(k是常数,k≠0),其中变量x、y的指数是1,函数表达式要化简,特殊情况y、k、x可以是整式。
典例解析
若正比例函数的自变量x等于-4时,函数y的值等于2.
(1)求正比例函数的解析式;
(2)求当x=6时函数y的值.
(2)当x=6时,y=-0.5 6=-3
∴函数y的值为-3.
解:(1)设正比例函数解析式是y=kx,
把x=-4,y=2代入解析式,得:
2=-4k,
解得:k=-0.5
∴正比例函数解析式是y=-0.5x
先设函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法叫做待定系数法
若y关于x-2成正比例函数,当x=3时,y=-4.
(1)试求出y与x的函数关系式;
(2)当y=2时,求x的值.
变式练习
解:(1)设正比例函数解析式是y=k( -2)
(2)当y=2时,2=-4 +8
解得:
∴
把 =3,y=-4代入解析式,得
-4=(3-2)k
解得:k=-4
∴函数解析式是y=-4 +8
汽车由天津驶往相距120km的北京,s(单位:km)表示汽车离开天津的距离,t(单位:h)表示汽车行驶的时间,s与t之间的正比例函数关系如图所示.
s/km
t/h
0
20
40
60
80
100
120
1
2
3
4
1.汽车用几小时可以到达北京?速度是多少?
2.汽车行驶1h,离开天津有多远?
3.当汽车距北京20km时,汽车出发了多长时间?
解:(1)4h, 速度:120 4=30(km/h)
(2)设s与t的函数关系式为
解得:
s与t的函数解析式为
实际应用
汽车行驶1h,离开天津有30km.
把t=4,s=120代入解析式得:
汽车由天津驶往相距120km的北京,s(单位:km)表示汽车离开天津的距离,t(单位:h)表示汽车行驶的时间,s与t之间的正比例函数关系如图所示.
3.当汽车距北京20km时,汽车出发了多长时间?
s/km
t/h
0
20
40
60
80
100
120
1
2
3
4
(3)当s=120-20=100时
当汽车距北京20km时汽车出发了 .
(2)30 1=30(km)
解:(1)4h, 速度:120 4=30(km/h)
(3)30t=120-20
解得:t=
汽车出发了 小时。
实际应用
课堂小结
课后作业
1.预习正比例函数图象性质,绘制一个平面直角坐标系.
4.已知正比例函数y=kx(k≠0),当x=3时,y=-15, 求k的值,并写出解析式。
2.若y=kx+2k-3是y关于x的正比例函数,则k=___.
3.若y=(k+3) 是y关于x的正比例函数,试求k的值,并指出正比例系数.
感
谢
聆
听
正比例函数的概念
人教版·初中数学·八年级下册·第十九章
19.2.1 正比例函数
学
习
目
标
1.理解正比例函数的概念;
2.会求正比例函数的解析式;
3.能利用正比例函数解决简单的实际问题.
下列问题中的变量对应规律可用怎样的函数解析式表示?
(1)圆的周长l随半径r的大小变化而变化.
(2)市场上苹果每千克7.5元,买苹果所需的钱数y(单位:元)随购买的数量x(单位:千克)的变化而变化.
解:l=2πr
解:y =7.5 x .
问题探究
(3)每个练习本的厚度为0.5cm,一些练习本摞在一起的总厚度h(单位:cm)随这些练习本的本数n的变化而变化.
(4)冷冻一个0℃的物体,使它每分下降2℃,物体的温度T
(单位:℃)随冷冻时间t(单位:分)的变化而变化.
解:h = 0.5n .
解:T=-2t.
问题探究
思考归纳
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量
函数=常数×自变量
这些函数解析式有什么共同点?
l
r
2π
y
7.5
x
T
-2
n
h
0.5
t
知识要点
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比
例函数,其中k叫做比例系数.
正比例函数解析式的特点:
(1)k是常数,k≠0 ;
(3)函数关系式的左边是函数、右边是常量与自变量的乘积。
(2)变量x、y的指数都是1;
下列式子,哪些表示y是x的正比例函数 如果是,请你指出比例系数k的值.
概念辨析
√
√
√
√
变式巩固
2.若y=(n-1)x|n|是正比例函数,则n= .
-1
1.如果y=3x+k-4,是y关于x的正比例函数,则k=_________.
4
-2
2
3.若 是正比例函数,则 m = .
4.若 是正比例函数,则 m = .
判断正比例函数:形式上要满足y=kx(k是常数,k≠0),其中变量x、y的指数是1,函数表达式要化简,特殊情况y、k、x可以是整式。
典例解析
若正比例函数的自变量x等于-4时,函数y的值等于2.
(1)求正比例函数的解析式;
(2)求当x=6时函数y的值.
(2)当x=6时,y=-0.5 6=-3
∴函数y的值为-3.
解:(1)设正比例函数解析式是y=kx,
把x=-4,y=2代入解析式,得:
2=-4k,
解得:k=-0.5
∴正比例函数解析式是y=-0.5x
先设函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法叫做待定系数法
若y关于x-2成正比例函数,当x=3时,y=-4.
(1)试求出y与x的函数关系式;
(2)当y=2时,求x的值.
变式练习
解:(1)设正比例函数解析式是y=k( -2)
(2)当y=2时,2=-4 +8
解得:
∴
把 =3,y=-4代入解析式,得
-4=(3-2)k
解得:k=-4
∴函数解析式是y=-4 +8
汽车由天津驶往相距120km的北京,s(单位:km)表示汽车离开天津的距离,t(单位:h)表示汽车行驶的时间,s与t之间的正比例函数关系如图所示.
s/km
t/h
0
20
40
60
80
100
120
1
2
3
4
1.汽车用几小时可以到达北京?速度是多少?
2.汽车行驶1h,离开天津有多远?
3.当汽车距北京20km时,汽车出发了多长时间?
解:(1)4h, 速度:120 4=30(km/h)
(2)设s与t的函数关系式为
解得:
s与t的函数解析式为
实际应用
汽车行驶1h,离开天津有30km.
把t=4,s=120代入解析式得:
汽车由天津驶往相距120km的北京,s(单位:km)表示汽车离开天津的距离,t(单位:h)表示汽车行驶的时间,s与t之间的正比例函数关系如图所示.
3.当汽车距北京20km时,汽车出发了多长时间?
s/km
t/h
0
20
40
60
80
100
120
1
2
3
4
(3)当s=120-20=100时
当汽车距北京20km时汽车出发了 .
(2)30 1=30(km)
解:(1)4h, 速度:120 4=30(km/h)
(3)30t=120-20
解得:t=
汽车出发了 小时。
实际应用
课堂小结
课后作业
1.预习正比例函数图象性质,绘制一个平面直角坐标系.
4.已知正比例函数y=kx(k≠0),当x=3时,y=-15, 求k的值,并写出解析式。
2.若y=kx+2k-3是y关于x的正比例函数,则k=___.
3.若y=(k+3) 是y关于x的正比例函数,试求k的值,并指出正比例系数.
感
谢
聆
听
