22.3 实际问题与二次函数 课件(20张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 22.3 实际问题与二次函数 课件(20张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
22.3实际问题与二次函数
年 级:九年级
学 科:初中数学(人教版)
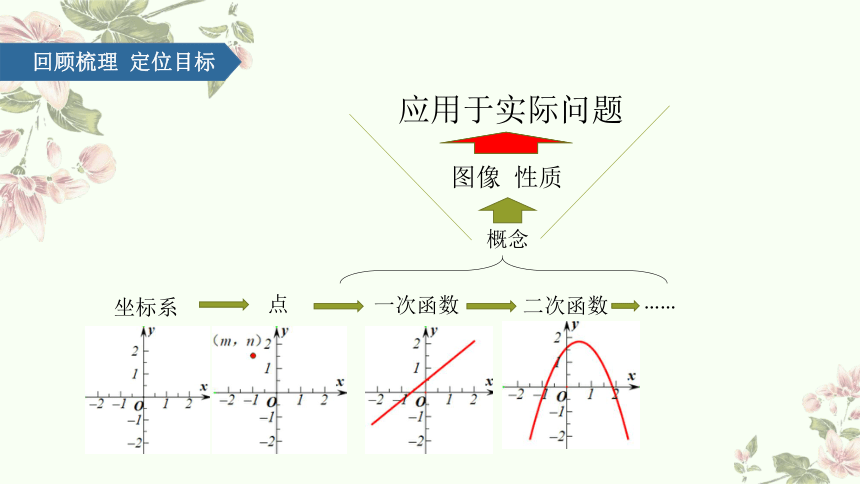
坐标系
点
一次函数
二次函数
……
概念
图像 性质
应用于实际问题
回顾梳理 定位目标
问题 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h= 30t-5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
当小球运动的时间是3s时,小球最高.小球运动中的最大高度是45m.
解:结合图形分析可知抛物线的顶点是这个函数的图象的最高点.
问题引导 感悟新知
当 时,
h有最大值 .
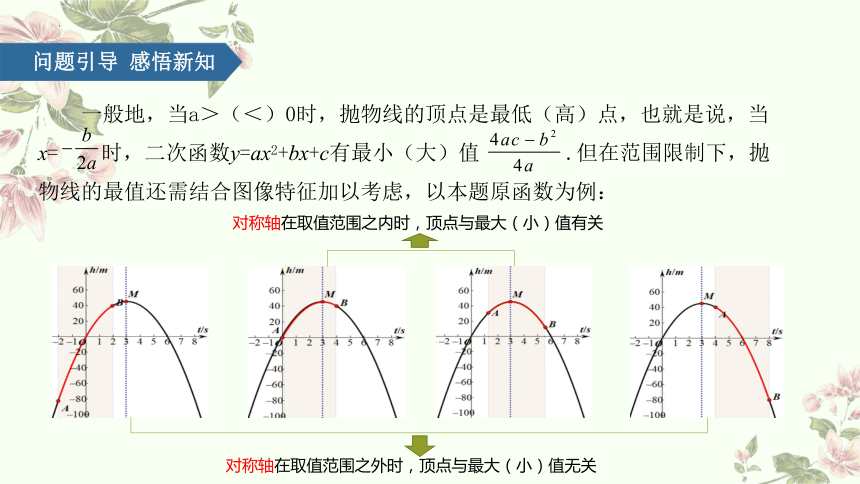
一般地,当a>(<)0时,抛物线的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值 .但在范围限制下,抛物线的最值还需结合图像特征加以考虑,以本题原函数为例:
对称轴在取值范围之内时,顶点与最大(小)值有关
对称轴在取值范围之外时,顶点与最大(小)值无关
问题引导 感悟新知
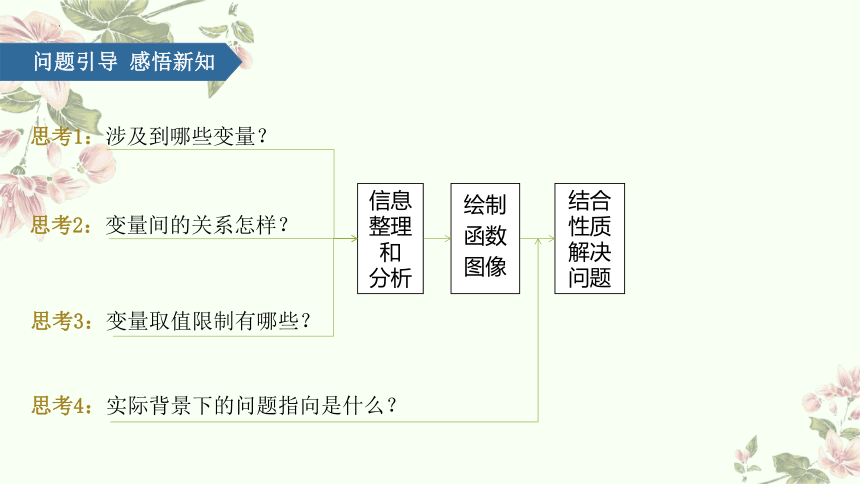
信息
整理和
分析
绘制函数图像
结合性质解决问题
思考1:涉及到哪些变量?
思考2:变量间的关系怎样?
思考3:变量取值限制有哪些?
思考4:实际背景下的问题指向是什么?
问题引导 感悟新知
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
思考1:涉及到哪些变量?
思考2:变量间的关系怎样?
矩形一边长为l m,另一边长为(30-l)m ,则面积S=l(30-l).
l
30-l
探究1(面积最值)
表示边长的l和表示面积的S.
思考3:变量取值限制有哪些?
思考4:实际背景下的问题指向是什么?
场地面积最大,就是函数S=l(30-l)在条件限制下能取到的最大值.
探究1(面积最值)
两条边长都要大于0.
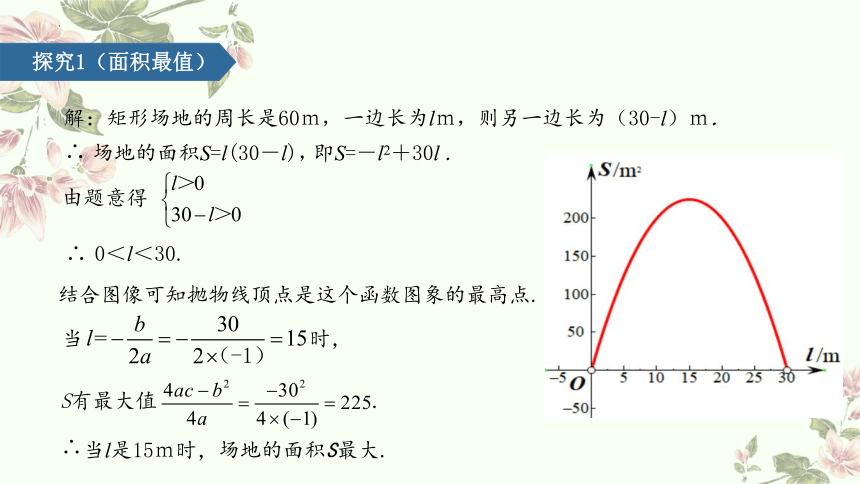
解:矩形场地的周长是60m,一边长为lm,则另一边长为(30-l)m.
即S=-l2+30l .
由题意得
S有最大值 .
探究1(面积最值)
场地的面积S=l(30-l),
当 时,
当l是15m时,场地的面积S最大.
0<l<30.
结合图像可知抛物线顶点是这个函数图象的最高点.
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
思考1:涉及到哪些变量?
价格与利润
原价+变动价格=售价 售价—成本=利润 总利润=单价利润×销售量
思考2:变量间关系怎样?
探究2(销售最值)
涨价
价格变化
单件售价
每星期销售变化
最终销售量
销售额
总成本
降价
价格变化 -m元/件
单件售价 (60-m)元/件
每星期销售变化 +20m件
最终销售量 (300+20m)件
销售额 (60-m)(300+20m)元
总成本 40(300+20m)元
涨价行为下的利润为y=(60+x )(300-10x )-40(300-10x )
降价行为下的利润为z=(60-m)(300+20m)-40(300+20m)
探究2(销售最值)
思考3:变量取值限制有哪些?
涨价
,降价
思考4:实际背景下的问题指向是什么?
探究2(销售最值)
涨价和降价两种不同的价格变动方式下,比较得出获利最大的价格变动方案.
解:设每件涨价x元,则每星期少卖10x件,实际卖出(300-10x)件,销售额为(60+x)(300-10x)元,买进商品需付40(300-10x)元.
当 时,
结合图像可知,在涨价的情况下,涨价5元,即定价为65元时,可以获得最大利润6250元。
探究2(销售最值)
y有最大值 .
所得利润y=(60+x)(300-10x)-40(300-10x).
即y=-10x2+100x+6000.
由题意得 ,
0≤x≤30.
结合图像可知抛物线顶点是这个函数图象的最高点.
再来看降价的情况,设每件降价m元,则每星期多卖20m件,实际卖出(300+20m)件,销售额为(60-m)(300+20m)元,买进商品需付40(300+20m)元。
所得利润z=(60-m)(300+20m)-40(300+20m)
即z =-20m2+100m+6000(00)
结合图像可知,在降价背景下,降价2.5元,即定价为57.5元时,可以获得最大利润6150元。
探究2(销售最值)
当 时,
z有最大值
所以,定价65元时利润最大.
探究2(销售最值)
因为6150<6250,
如图是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m ,水面宽度增加多少?
探究3(建坐标系)
思考1:涉及到哪些变量?
思考2:变量间关系怎样?
水位高低与水面宽度.
二次函数关系.
x
y
x
x
x
y
y
y
y=ax(x-4)
y=ax(x+4)
y=ax2+2
y=ax2
o
o
o
以1m为1个单位长度
探究3(建坐标系)
o
如图是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m,水面宽度增加多少?
探究3(建坐标系)
思考3:变量取值限制有哪些?
没有明确限制.
抛物线上纵坐标等于-2的两点间距离与纵坐标等于-3的两点间距离的变化情况.
思考4:实际背景下的问题指向是什么?
解:以抛物线顶点为原点,抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),
这条抛物线表示的二次函数为y= x2
当水面下降1m时,水面的纵坐标为-3,
可将y=-3代入函数y= x2,
可得x= ,实际水面宽度为 m,
水面宽度增加( )m.
结合实际情况建立适当的坐标系,更有利于问题的解决,需要统筹考虑:
1.解析式表达更简洁.
2.条件使用更便捷.
3.问题解决更直接.
探究3(建坐标系)
可得-2=a×22,a=
实际问题
归纳、抽象
回顾总结 感悟反思
二次函数模型
实际问题答案
利用函数图像和性质解题
目标
思考1:确定变量
思考2:确定函数解析式
思考3:确定变量限制
思考4:
确定问
题指向
同学们,再见!
22.3实际问题与二次函数
年 级:九年级
学 科:初中数学(人教版)
坐标系
点
一次函数
二次函数
……
概念
图像 性质
应用于实际问题
回顾梳理 定位目标
问题 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h= 30t-5t2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
当小球运动的时间是3s时,小球最高.小球运动中的最大高度是45m.
解:结合图形分析可知抛物线的顶点是这个函数的图象的最高点.
问题引导 感悟新知
当 时,
h有最大值 .
一般地,当a>(<)0时,抛物线的顶点是最低(高)点,也就是说,当x= 时,二次函数y=ax2+bx+c有最小(大)值 .但在范围限制下,抛物线的最值还需结合图像特征加以考虑,以本题原函数为例:
对称轴在取值范围之内时,顶点与最大(小)值有关
对称轴在取值范围之外时,顶点与最大(小)值无关
问题引导 感悟新知
信息
整理和
分析
绘制函数图像
结合性质解决问题
思考1:涉及到哪些变量?
思考2:变量间的关系怎样?
思考3:变量取值限制有哪些?
思考4:实际背景下的问题指向是什么?
问题引导 感悟新知
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
思考1:涉及到哪些变量?
思考2:变量间的关系怎样?
矩形一边长为l m,另一边长为(30-l)m ,则面积S=l(30-l).
l
30-l
探究1(面积最值)
表示边长的l和表示面积的S.
思考3:变量取值限制有哪些?
思考4:实际背景下的问题指向是什么?
场地面积最大,就是函数S=l(30-l)在条件限制下能取到的最大值.
探究1(面积最值)
两条边长都要大于0.
解:矩形场地的周长是60m,一边长为lm,则另一边长为(30-l)m.
即S=-l2+30l .
由题意得
S有最大值 .
探究1(面积最值)
场地的面积S=l(30-l),
当 时,
当l是15m时,场地的面积S最大.
0<l<30.
结合图像可知抛物线顶点是这个函数图象的最高点.
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出20件.已知商品的进价为每件40元,如何定价才能使利润最大?
思考1:涉及到哪些变量?
价格与利润
原价+变动价格=售价 售价—成本=利润 总利润=单价利润×销售量
思考2:变量间关系怎样?
探究2(销售最值)
涨价
价格变化
单件售价
每星期销售变化
最终销售量
销售额
总成本
降价
价格变化 -m元/件
单件售价 (60-m)元/件
每星期销售变化 +20m件
最终销售量 (300+20m)件
销售额 (60-m)(300+20m)元
总成本 40(300+20m)元
涨价行为下的利润为y=(60+x )(300-10x )-40(300-10x )
降价行为下的利润为z=(60-m)(300+20m)-40(300+20m)
探究2(销售最值)
思考3:变量取值限制有哪些?
涨价
,降价
思考4:实际背景下的问题指向是什么?
探究2(销售最值)
涨价和降价两种不同的价格变动方式下,比较得出获利最大的价格变动方案.
解:设每件涨价x元,则每星期少卖10x件,实际卖出(300-10x)件,销售额为(60+x)(300-10x)元,买进商品需付40(300-10x)元.
当 时,
结合图像可知,在涨价的情况下,涨价5元,即定价为65元时,可以获得最大利润6250元。
探究2(销售最值)
y有最大值 .
所得利润y=(60+x)(300-10x)-40(300-10x).
即y=-10x2+100x+6000.
由题意得 ,
0≤x≤30.
结合图像可知抛物线顶点是这个函数图象的最高点.
再来看降价的情况,设每件降价m元,则每星期多卖20m件,实际卖出(300+20m)件,销售额为(60-m)(300+20m)元,买进商品需付40(300+20m)元。
所得利润z=(60-m)(300+20m)-40(300+20m)
即z =-20m2+100m+6000(00)
结合图像可知,在降价背景下,降价2.5元,即定价为57.5元时,可以获得最大利润6150元。
探究2(销售最值)
当 时,
z有最大值
所以,定价65元时利润最大.
探究2(销售最值)
因为6150<6250,
如图是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m ,水面宽度增加多少?
探究3(建坐标系)
思考1:涉及到哪些变量?
思考2:变量间关系怎样?
水位高低与水面宽度.
二次函数关系.
x
y
x
x
x
y
y
y
y=ax(x-4)
y=ax(x+4)
y=ax2+2
y=ax2
o
o
o
以1m为1个单位长度
探究3(建坐标系)
o
如图是抛物线形拱桥,当拱顶离水面2m,水面宽4m,水面下降1m,水面宽度增加多少?
探究3(建坐标系)
思考3:变量取值限制有哪些?
没有明确限制.
抛物线上纵坐标等于-2的两点间距离与纵坐标等于-3的两点间距离的变化情况.
思考4:实际背景下的问题指向是什么?
解:以抛物线顶点为原点,抛物线的对称轴为y轴建立直角坐标系.
设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),
这条抛物线表示的二次函数为y= x2
当水面下降1m时,水面的纵坐标为-3,
可将y=-3代入函数y= x2,
可得x= ,实际水面宽度为 m,
水面宽度增加( )m.
结合实际情况建立适当的坐标系,更有利于问题的解决,需要统筹考虑:
1.解析式表达更简洁.
2.条件使用更便捷.
3.问题解决更直接.
探究3(建坐标系)
可得-2=a×22,a=
实际问题
归纳、抽象
回顾总结 感悟反思
二次函数模型
实际问题答案
利用函数图像和性质解题
目标
思考1:确定变量
思考2:确定函数解析式
思考3:确定变量限制
思考4:
确定问
题指向
同学们,再见!
同课章节目录
