24.2.2 直线和圆的位置关系 教案 2023-2024学年人教版九年级数学上册(表格式)
文档属性
| 名称 | 24.2.2 直线和圆的位置关系 教案 2023-2024学年人教版九年级数学上册(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 664.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 11:38:39 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 初中数学 年级 九年级 学期 秋季
课题 点和圆、直线和圆的位置关系
教科书 书 名:数学教材 出版社:人民教育出版社
教学目标
1.了解直线和圆的三种位置关系、切线的判定定理和性质定理、切线长定理,了解三角形的内切圆及三角形内心的概念。 2.能根据给出的条件判断直线和圆的三种位置关系,能用定理证明简单的几何问题。 3.经历定量刻画直线和圆的位置关系、三角形的内切圆的探索过程,培养学生的探索能力,并在探索中,进一步体会解决数学问题的策略。
教学内容
教学重点: 直线和圆的位置关系,切线的判定定理和性质定理、切线长定理。
教学难点: 经历定量刻画直线和圆的位置关系,并能作三角形的内切圆。
教学过程
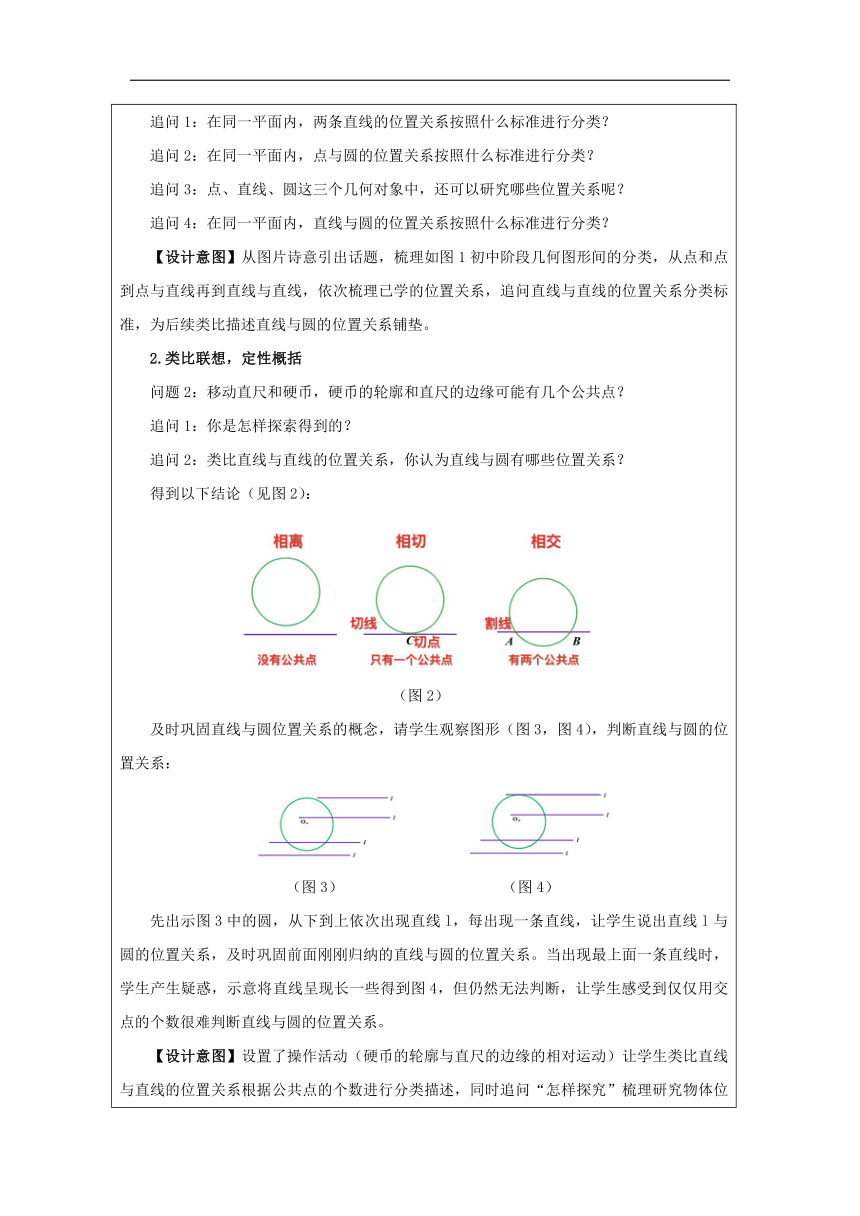
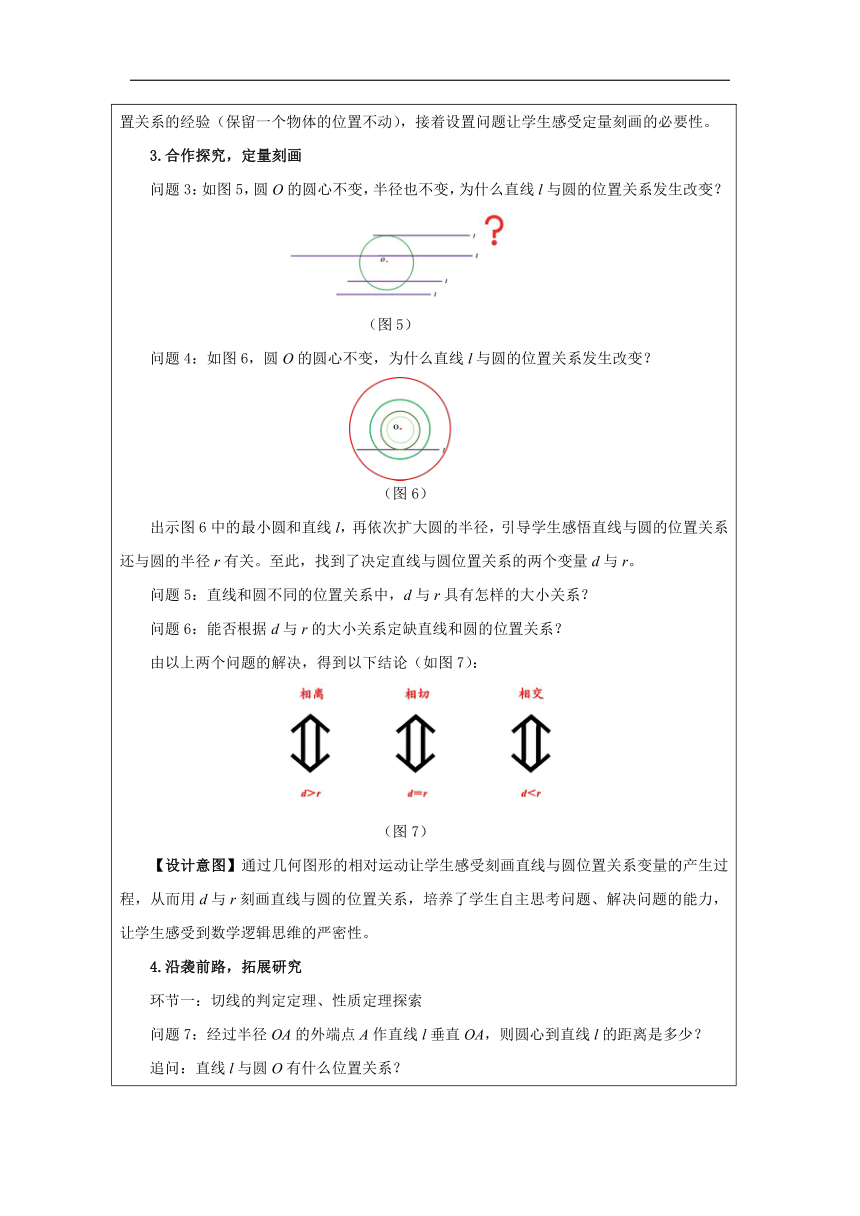
1.实物抽象,梳理关系 问题1:从生活实物抽象几何图形之间的关系类别 出示含小鸟、太阳、电线的唯美图片,引导学生把实物抽象成几何图形,逐步整理出图形间的关系类别,见图1。 (图1) 追问1:在同一平面内,两条直线的位置关系按照什么标准进行分类? 追问2:在同一平面内,点与圆的位置关系按照什么标准进行分类? 追问3:点、直线、圆这三个几何对象中,还可以研究哪些位置关系呢? 追问4:在同一平面内,直线与圆的位置关系按照什么标准进行分类? 【设计意图】从图片诗意引出话题,梳理如图1初中阶段几何图形间的分类,从点和点到点与直线再到直线与直线,依次梳理已学的位置关系,追问直线与直线的位置关系分类标准,为后续类比描述直线与圆的位置关系铺垫。 2.类比联想,定性概括 问题2:移动直尺和硬币,硬币的轮廓和直尺的边缘可能有几个公共点? 追问1:你是怎样探索得到的? 追问2:类比直线与直线的位置关系,你认为直线与圆有哪些位置关系? 得到以下结论(见图2): (图2) 及时巩固直线与圆位置关系的概念,请学生观察图形(图3,图4),判断直线与圆的位置关系: (图3) (图4) 先出示图3中的圆,从下到上依次出现直线l,每出现一条直线,让学生说出直线l与圆的位置关系,及时巩固前面刚刚归纳的直线与圆的位置关系。当出现最上面一条直线时,学生产生疑惑,示意将直线呈现长一些得到图4,但仍然无法判断,让学生感受到仅仅用交点的个数很难判断直线与圆的位置关系。 【设计意图】设置了操作活动(硬币的轮廓与直尺的边缘的相对运动)让学生类比直线与直线的位置关系根据公共点的个数进行分类描述,同时追问“怎样探究”梳理研究物体位置关系的经验(保留一个物体的位置不动),接着设置问题让学生感受定量刻画的必要性。 3.合作探究,定量刻画 问题3:如图5,圆O的圆心不变,半径也不变,为什么直线l与圆的位置关系发生改变? (图5) 问题4:如图6,圆O的圆心不变,为什么直线l与圆的位置关系发生改变? (图6) 出示图6中的最小圆和直线l,再依次扩大圆的半径,引导学生感悟直线与圆的位置关系还与圆的半径r有关。至此,找到了决定直线与圆位置关系的两个变量d与r。 问题5:直线和圆不同的位置关系中,d与r具有怎样的大小关系? 问题6:能否根据d与r的大小关系定缺直线和圆的位置关系? 由以上两个问题的解决,得到以下结论(如图7): (图7) 【设计意图】通过几何图形的相对运动让学生感受刻画直线与圆位置关系变量的产生过程,从而用d与r刻画直线与圆的位置关系,培养了学生自主思考问题、解决问题的能力,让学生感受到数学逻辑思维的严密性。 4.沿袭前路,拓展研究 环节一:切线的判定定理、性质定理探索 问题7:经过半径OA的外端点A作直线l垂直OA,则圆心到直线l的距离是多少? 追问:直线l与圆O有什么位置关系? 由一个问题及追问得到切线的判定定理,并配备一道练习(见图8),巩固反思用切线的判定定理时要注意的两点。 (图8) 问题8:直线l是圆O的切线,切点为A,那么OA与直线l是否一定垂直? 由此问题得到切线的性质定理,并配备例1(见图9)巩固切线的判定定理、性质定理,并及时反思得到:在解决有关圆的切线问题时,常常需要作过切点的半径和判断切线的方法、性质。 (图9) 环节二:切线长定理探索 问题9:PA,PB是⊙O的两条切线,切点分别为A,B.图中的PA与PB,∠APO与∠BPO有什么关系? 由此问题得到切线长定理 环节三:三角形的内切圆探索 问题10:如何在一块三角形的铁皮上截下一块圆形用料,并且使截下来的圆与三角形的三边都相切? 由此问题得到三角形的内切圆等相关概念,并配备例2(见图10)巩固切线长定理及三角形的内切圆。 (图10) 【设计意图】三个环节,沿袭一条直线和圆相切,过圆外一点两条直线和圆相切,三条直线和圆相切的路径,依次探索相关定理,让学生进一步感受几何图形的研究路径及方向,培养探索解决问题的能力。 5.梳理知识,反思提升 如图11、图12,引导学生回顾直和圆的三种位置关系及判定方法,梳理研究的路径及方向,并引导学生思考其他几何图形的位置关系研究…… (图11) (图12) 【设计意图】回顾本节课所学的知识点,通过全面梳理本课研究路径,让学生从系统的角度归纳几何图形位置关系的量化方法。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
课程基本信息
学科 初中数学 年级 九年级 学期 秋季
课题 点和圆、直线和圆的位置关系
教科书 书 名:数学教材 出版社:人民教育出版社
教学目标
1.了解直线和圆的三种位置关系、切线的判定定理和性质定理、切线长定理,了解三角形的内切圆及三角形内心的概念。 2.能根据给出的条件判断直线和圆的三种位置关系,能用定理证明简单的几何问题。 3.经历定量刻画直线和圆的位置关系、三角形的内切圆的探索过程,培养学生的探索能力,并在探索中,进一步体会解决数学问题的策略。
教学内容
教学重点: 直线和圆的位置关系,切线的判定定理和性质定理、切线长定理。
教学难点: 经历定量刻画直线和圆的位置关系,并能作三角形的内切圆。
教学过程
1.实物抽象,梳理关系 问题1:从生活实物抽象几何图形之间的关系类别 出示含小鸟、太阳、电线的唯美图片,引导学生把实物抽象成几何图形,逐步整理出图形间的关系类别,见图1。 (图1) 追问1:在同一平面内,两条直线的位置关系按照什么标准进行分类? 追问2:在同一平面内,点与圆的位置关系按照什么标准进行分类? 追问3:点、直线、圆这三个几何对象中,还可以研究哪些位置关系呢? 追问4:在同一平面内,直线与圆的位置关系按照什么标准进行分类? 【设计意图】从图片诗意引出话题,梳理如图1初中阶段几何图形间的分类,从点和点到点与直线再到直线与直线,依次梳理已学的位置关系,追问直线与直线的位置关系分类标准,为后续类比描述直线与圆的位置关系铺垫。 2.类比联想,定性概括 问题2:移动直尺和硬币,硬币的轮廓和直尺的边缘可能有几个公共点? 追问1:你是怎样探索得到的? 追问2:类比直线与直线的位置关系,你认为直线与圆有哪些位置关系? 得到以下结论(见图2): (图2) 及时巩固直线与圆位置关系的概念,请学生观察图形(图3,图4),判断直线与圆的位置关系: (图3) (图4) 先出示图3中的圆,从下到上依次出现直线l,每出现一条直线,让学生说出直线l与圆的位置关系,及时巩固前面刚刚归纳的直线与圆的位置关系。当出现最上面一条直线时,学生产生疑惑,示意将直线呈现长一些得到图4,但仍然无法判断,让学生感受到仅仅用交点的个数很难判断直线与圆的位置关系。 【设计意图】设置了操作活动(硬币的轮廓与直尺的边缘的相对运动)让学生类比直线与直线的位置关系根据公共点的个数进行分类描述,同时追问“怎样探究”梳理研究物体位置关系的经验(保留一个物体的位置不动),接着设置问题让学生感受定量刻画的必要性。 3.合作探究,定量刻画 问题3:如图5,圆O的圆心不变,半径也不变,为什么直线l与圆的位置关系发生改变? (图5) 问题4:如图6,圆O的圆心不变,为什么直线l与圆的位置关系发生改变? (图6) 出示图6中的最小圆和直线l,再依次扩大圆的半径,引导学生感悟直线与圆的位置关系还与圆的半径r有关。至此,找到了决定直线与圆位置关系的两个变量d与r。 问题5:直线和圆不同的位置关系中,d与r具有怎样的大小关系? 问题6:能否根据d与r的大小关系定缺直线和圆的位置关系? 由以上两个问题的解决,得到以下结论(如图7): (图7) 【设计意图】通过几何图形的相对运动让学生感受刻画直线与圆位置关系变量的产生过程,从而用d与r刻画直线与圆的位置关系,培养了学生自主思考问题、解决问题的能力,让学生感受到数学逻辑思维的严密性。 4.沿袭前路,拓展研究 环节一:切线的判定定理、性质定理探索 问题7:经过半径OA的外端点A作直线l垂直OA,则圆心到直线l的距离是多少? 追问:直线l与圆O有什么位置关系? 由一个问题及追问得到切线的判定定理,并配备一道练习(见图8),巩固反思用切线的判定定理时要注意的两点。 (图8) 问题8:直线l是圆O的切线,切点为A,那么OA与直线l是否一定垂直? 由此问题得到切线的性质定理,并配备例1(见图9)巩固切线的判定定理、性质定理,并及时反思得到:在解决有关圆的切线问题时,常常需要作过切点的半径和判断切线的方法、性质。 (图9) 环节二:切线长定理探索 问题9:PA,PB是⊙O的两条切线,切点分别为A,B.图中的PA与PB,∠APO与∠BPO有什么关系? 由此问题得到切线长定理 环节三:三角形的内切圆探索 问题10:如何在一块三角形的铁皮上截下一块圆形用料,并且使截下来的圆与三角形的三边都相切? 由此问题得到三角形的内切圆等相关概念,并配备例2(见图10)巩固切线长定理及三角形的内切圆。 (图10) 【设计意图】三个环节,沿袭一条直线和圆相切,过圆外一点两条直线和圆相切,三条直线和圆相切的路径,依次探索相关定理,让学生进一步感受几何图形的研究路径及方向,培养探索解决问题的能力。 5.梳理知识,反思提升 如图11、图12,引导学生回顾直和圆的三种位置关系及判定方法,梳理研究的路径及方向,并引导学生思考其他几何图形的位置关系研究…… (图11) (图12) 【设计意图】回顾本节课所学的知识点,通过全面梳理本课研究路径,让学生从系统的角度归纳几何图形位置关系的量化方法。
备注:教学设计应至少含教学目标、教学内容、教学过程等三个部分,如有其它内容,可自行补充增加。
同课章节目录
