青岛版八年级上册数学第1章1.1全等三角形(14张PPT)
文档属性
| 名称 | 青岛版八年级上册数学第1章1.1全等三角形(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-09 00:00:00 | ||
图片预览





文档简介
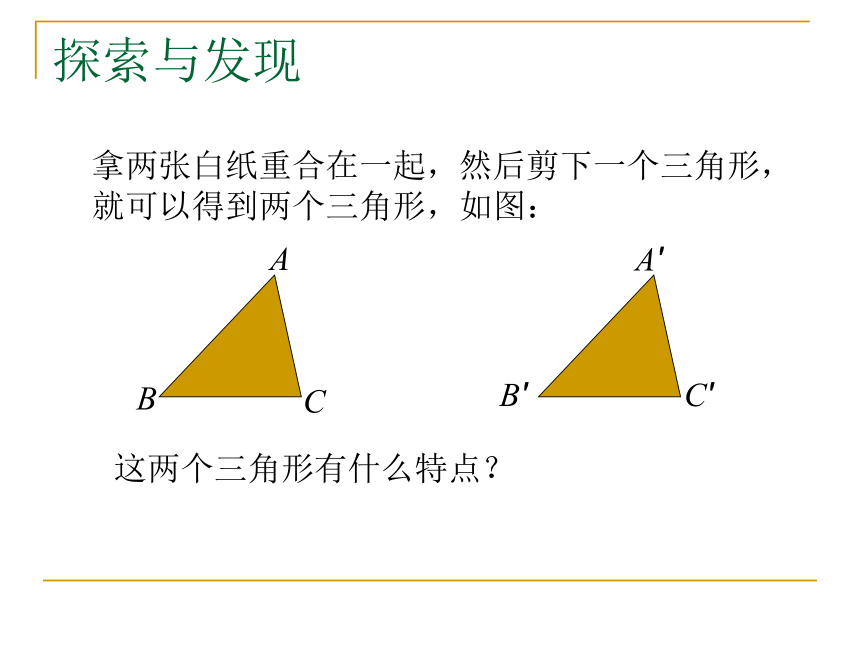
课件14张PPT。1.1 全等三角形探索与发现拿两张白纸重合在一起,然后剪下一个三角形,
就可以得到两个三角形,如图:BACA′B′C′这两个三角形有什么特点?
观察与思考 能够完全重合的两个三角形称为全等三角形。
记作:△ABC≌△A1B1C1 当两个全等三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.
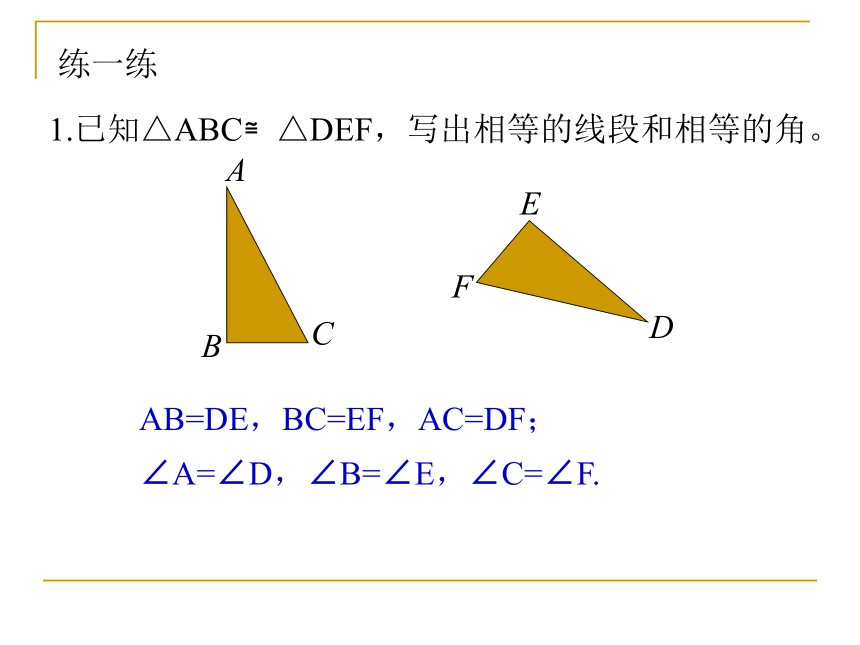
对应角:∠A和∠A1,∠B和∠B1, ∠C和∠C1.对应顶点:点A和点A1,点B和点B1,点C和点C1.对应边:AB和A1B1,AC和A1C1,BC和B1C1.观察与思考观察与思考 观察下图中的两个三角形,哪些边分别对应相等,哪些角分别对应相等?结论:全等三角形的对应边相等,对应角相等。练一练1.已知△ABC≌△DEF,写出相等的线段和相等的角。BACFEDAB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F. 如图,已知△ADC≌△CBA,
写出图中相等的边、相等的角。例1解∵ △ADC≌△CBA∴ AB=CD,AC=CA,AD=CB(全等三角形的对应边相等)∠CAD=∠ACB,∠B=∠D
∠BAC=∠ACD(全等三角形的对应角相等) 2.如图,已知△AOB≌△COD,
写出图中相等的边、相等的角。练一练解∵ △AOB≌△COD,∴ AB=CD,AO=CO,BO=DO;(全等三角形的对应边相等)∠AOB=∠COD,∠B=∠D,∠A=∠C.(全等三角形的对应角相等) 3.如图,已知△AEB≌△CED,
写出图中相等的边、相等的角。练一练解∵ △AEB≌△CED,∴ AB=CD,AE=CE,BE=DE;(全等三角形的对应边相等)∠ABE=∠CDE,∠E=∠E,∠A=∠C.(全等三角形的对应角相等)BACDE 如图,已知△ABC≌△DCB,
AB=7,BD=5,∠A=60°,求线段
DC、AC和∠D.例2解∵ △ABC≌△DCB∴ DC=AB=7,AC=BD=5;(全等三角形的对应边相等)∠D=∠A=60°.(全等三角形的对应角相等)4.如图,已知△ABC≌△DBE,
AB=8,BE=6,∠C=55°,
求线段DB、BC和∠BED.解∵ △ABC≌△DBE∴ DB=AB=8,BC=BE=6;(全等三角形的对应边相等)∠BED=∠C=55°.(全等三角形的对应角相等)练一练小结与思考全等三角形:对应顶点:
对应边:
对应角:怎样找全等三角形的对应边和对应角?全等三角形的对应边和对应角有什么关系?作业习题1.1的1、2、3
就可以得到两个三角形,如图:BACA′B′C′这两个三角形有什么特点?
观察与思考 能够完全重合的两个三角形称为全等三角形。
记作:△ABC≌△A1B1C1 当两个全等三角形完全重合时,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角.
对应角:∠A和∠A1,∠B和∠B1, ∠C和∠C1.对应顶点:点A和点A1,点B和点B1,点C和点C1.对应边:AB和A1B1,AC和A1C1,BC和B1C1.观察与思考观察与思考 观察下图中的两个三角形,哪些边分别对应相等,哪些角分别对应相等?结论:全等三角形的对应边相等,对应角相等。练一练1.已知△ABC≌△DEF,写出相等的线段和相等的角。BACFEDAB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F. 如图,已知△ADC≌△CBA,
写出图中相等的边、相等的角。例1解∵ △ADC≌△CBA∴ AB=CD,AC=CA,AD=CB(全等三角形的对应边相等)∠CAD=∠ACB,∠B=∠D
∠BAC=∠ACD(全等三角形的对应角相等) 2.如图,已知△AOB≌△COD,
写出图中相等的边、相等的角。练一练解∵ △AOB≌△COD,∴ AB=CD,AO=CO,BO=DO;(全等三角形的对应边相等)∠AOB=∠COD,∠B=∠D,∠A=∠C.(全等三角形的对应角相等) 3.如图,已知△AEB≌△CED,
写出图中相等的边、相等的角。练一练解∵ △AEB≌△CED,∴ AB=CD,AE=CE,BE=DE;(全等三角形的对应边相等)∠ABE=∠CDE,∠E=∠E,∠A=∠C.(全等三角形的对应角相等)BACDE 如图,已知△ABC≌△DCB,
AB=7,BD=5,∠A=60°,求线段
DC、AC和∠D.例2解∵ △ABC≌△DCB∴ DC=AB=7,AC=BD=5;(全等三角形的对应边相等)∠D=∠A=60°.(全等三角形的对应角相等)4.如图,已知△ABC≌△DBE,
AB=8,BE=6,∠C=55°,
求线段DB、BC和∠BED.解∵ △ABC≌△DBE∴ DB=AB=8,BC=BE=6;(全等三角形的对应边相等)∠BED=∠C=55°.(全等三角形的对应角相等)练一练小结与思考全等三角形:对应顶点:
对应边:
对应角:怎样找全等三角形的对应边和对应角?全等三角形的对应边和对应角有什么关系?作业习题1.1的1、2、3
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
