1.2.2矩形的性质与判定课件

课件22张PPT。方正之中感受数学之美1.2矩形的性质与判定（2）义务教育教科书（北师大版）数学 九年级上册第一章 特殊平行四边形同学们，以上出现的都是什么图形？ 一天,小丽和小娟
到一个商店准备给今天
要过生日的小华买生日
礼物,选了半天,她们俩
最后决定买相框送给她,
在里面摆放她们三个的
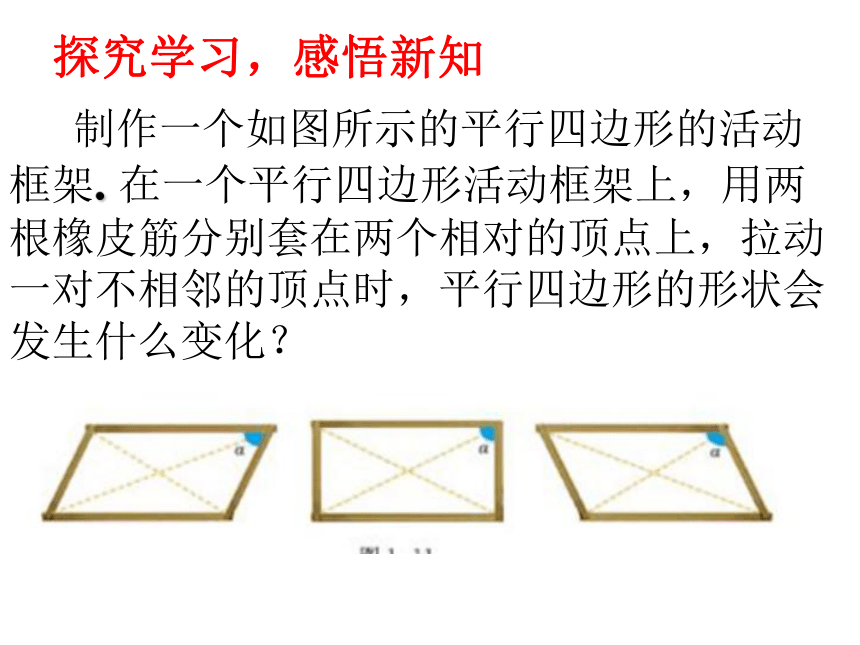
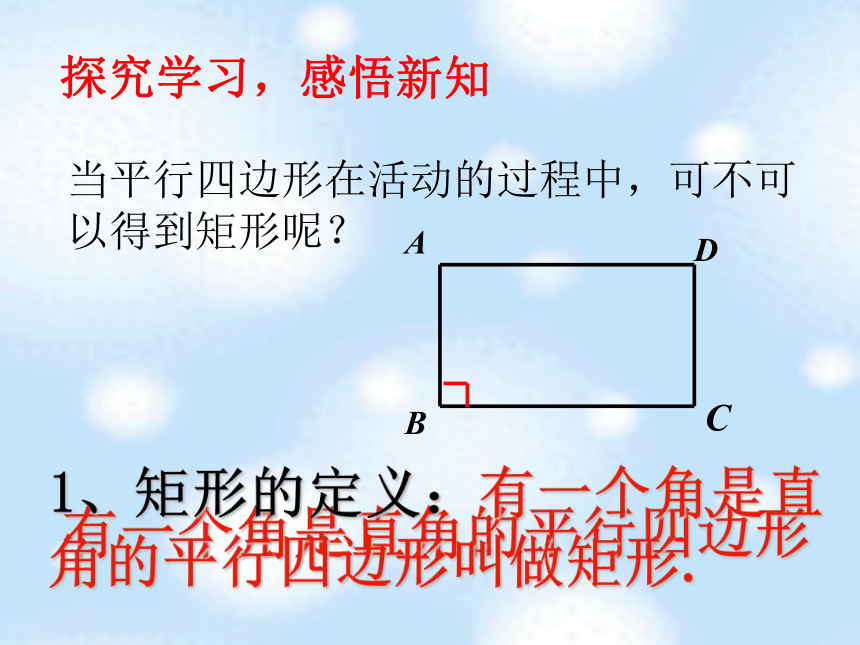
相片,为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法可以知道她们拿的就是矩形相框呢?创设情境，导入新课 制作一个如图所示的平行四边形的活动框架. 在一个平行四边形活动框架上，用两根橡皮筋分别套在两个相对的顶点上，拉动一对不相邻的顶点时，平行四边形的形状会发生什么变化？探究学习，感悟新知 有一个角是直角的平行四边形1、矩形的定义：有一个角是直角的平行四边形叫做矩形.探究学习，感悟新知 当平行四边形在活动的过程中，可不可以得到矩形呢？判定一.
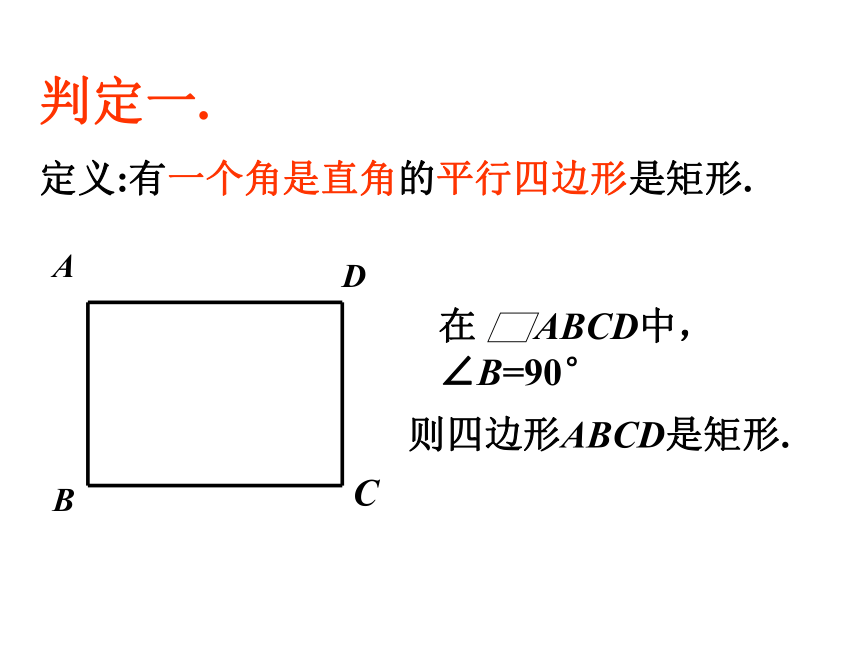
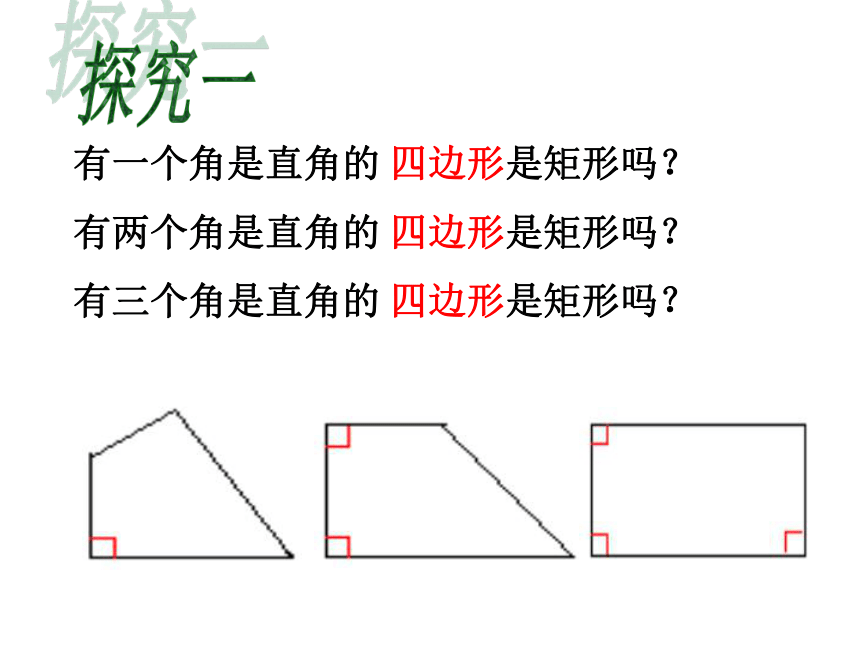
定义:有一个角是直角的平行四边形是矩形. 则四边形ABCD是矩形.有一个角是直角的 四边形是矩形吗？
有两个角是直角的 四边形是矩形吗？
有三个角是直角的 四边形是矩形吗？
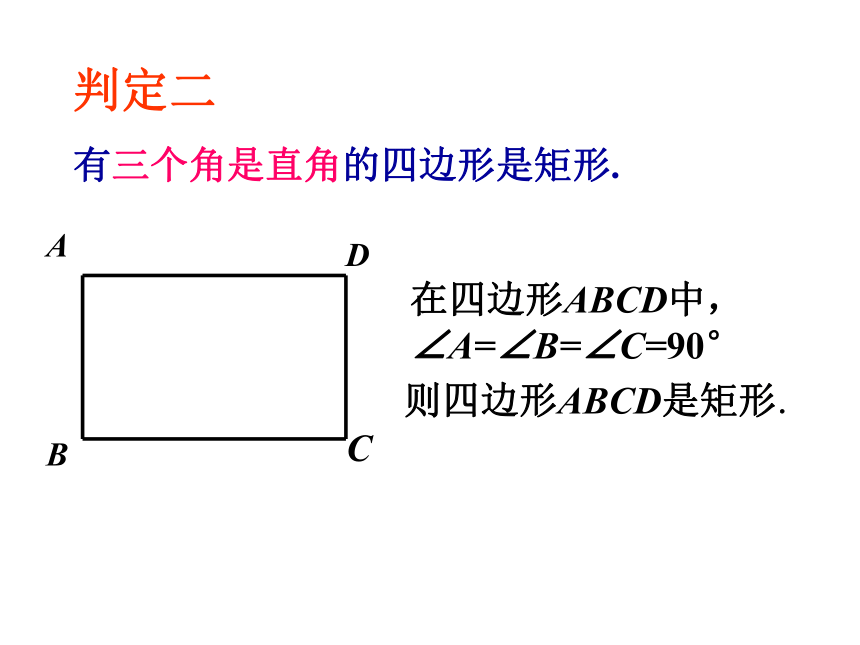
探究一判定二
有三个角是直角的四边形是矩形.在四边形ABCD中，∠A=∠B=∠C=90°则四边形ABCD是矩形． 已知：平行四边形ABCD，AC=BD．
求证：四边形ABCD是矩形． 证明: ∵ AB=CD, BC=BC, AC=BD∴ △ABC≌ △DCB（SSS）∵ AB//CD
∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形∴四边形ABCD是矩形． ∴ ∠ABC=∠DCB探究二判定三
对角线相等的平行四边形是矩形.则四边形ABCD是矩形． 交流提升,拓展新知思考：(1)对角线相等的四边形是矩形吗? (2)需要添加什么条件才能使 对角线相等的四边形是矩形吗?归纳：对角线相等且互相平分的四边形
是矩形 ∵ AC=BD
且OA=OC OB=OD
∴四边形ABCD是矩形． 等腰梯形问题解决1、如果让你帮助她们，用什么方法可以知道她们拿的就是矩形相框呢?
2、如果手中只有一根绳子作为工具，那么如何判断呢？例：已知如图四边形ABCD中AB⊥BC，AD∥BC，AD=BC，试说明四边形ABCD是矩形． 证明：∵ AD=CB AD∥CB
∴四边形ABCD是平行四边形
∵AB⊥BC
∴∠B=90°
∴ □ ABCD是矩形练习：已知如图四边形ABCD中
AO=BO=CO=DO，试说明四
边形ABCD是矩形． 范例点击，应用所学 1.一个角是直角的平行四边形是矩形．
2.三个角是直角是四边形是矩形．
3.对角线相等的平行四边形是矩形．
矩形的三种判定方法归纳总结，及时落实课堂总结，发展潜能判定一个四边形是矩形的方法与思路是：达标检测：1、判断下列说法是否正确？⑴对角线相等的四边形是矩形； （ ）⑵对角线互相平分且相等的四边形是矩形（ ）⑶有一个角是直角的四边形是矩形； （ ）⑷有三个角是直角的四边形是矩形； （ ）⑸四个角都相等的四边形是矩形； （ ）⑹对角线相等，且有一个角是直角的四边形
是矩形； （ ）⑺对角线相等且互相垂直的四边形是矩形． （ ）
2． 的平行四边形是矩形．
对角线 的平行四边形是矩形．有三个角是直角的四边形是 形．
对角线 的四边形是矩形．达标检测 提升自我3．如图，工人师傅做铝合金窗框分下面几个步骤进行：(1)先截出两对符合规格的铝合金窗(如图①)使AB=CD、 EF=GH； (2)摆放成(如图②)的四边形，则这时窗框的形状是 ，根据的数学道理是 ． (3)将直角尺靠紧窗框的一个角(如图③)调整窗框的边框，当直角尺的两条直角边与窗框无缝隙时(如图④)，说明窗框合格这时窗框是 ，根据的数学道理是 ． 4、如图，平行四边形ABCD中，AB= 6，BC= 8，AC= 10 ，
求证 : 四边形ABCD是矩形． 作业: 必做题：课本16页习题1.5第1题、第2题．选做题：1．课本16页，习题1.5第3题．2．用一根绳子可以判定一个四边形是不是矩形，那么用一根绳子可不可以判定平行四边形，菱形？课下小组同学讨论解决．