人教版数学八年级上册13.3.1等腰三角形的性质 课件(共25张PPT)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形的性质 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
匈牙利 赛格德教堂
法国巴黎 卢浮宫
埃及 金字塔
武汉长江二桥
从数学的观点去思考,这些图片都含有相同的几何图形吗?
这些三角形有什么特点?
13.3.1 等腰三角形的性质
A
B
C
1.等腰三角形:
有两条边相等的三角形
叫做等腰三角形。
等腰三角形的概念
2.相等的两条边叫做 腰
另一条边叫做 底边
底边与腰的夹角叫做底角
3.两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
自主学习
预习课本,找出什么叫等腰三角形?腰?底边?顶角?底角?
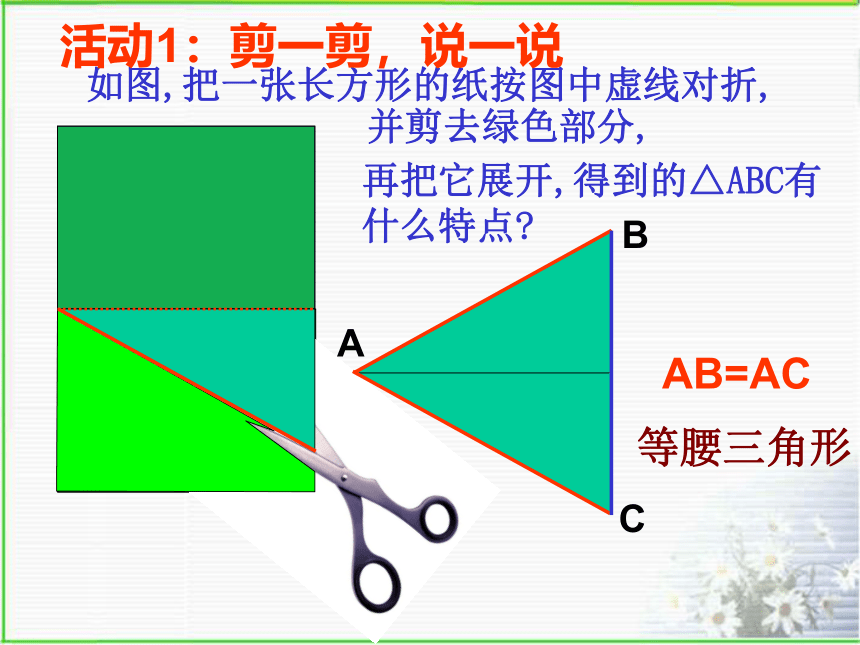
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
等腰三角形
活动1:剪一剪,说一说
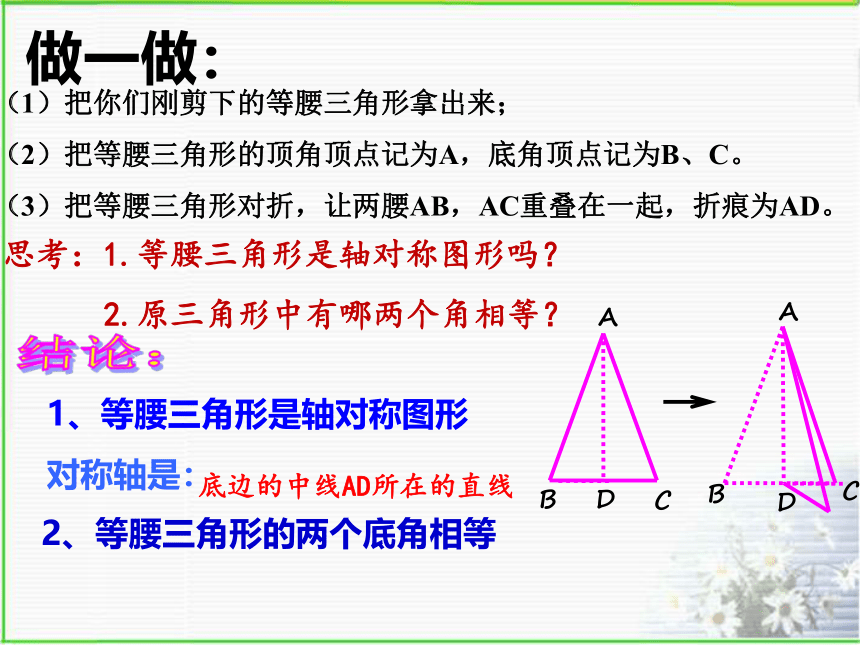
做一做:
(1)把你们刚剪下的等腰三角形拿出来;
(2)把等腰三角形的顶角顶点记为A,底角顶点记为B、C。
(3)把等腰三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
思考:1.等腰三角形是轴对称图形吗?
2.原三角形中有哪两个角相等?
B
A
C
D
A
B
C
D
结论:
1、等腰三角形是轴对称图形
2、等腰三角形的两个底角相等
对称轴是:
底边的中线AD所在的直线
推理论证:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
证明两个角相等有什么常见的方法:
三角形全等
如何构造两个全等的三角形?
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一:
做顶角∠BAC的平分线AD
已知:△ABC中,AB=AC求证:∠B= C
证明:
过A做AD⊥BC,垂足为D
C
A
B
D
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴∠B=∠C
∴ Rt△ABD ≌ Rt△ACD(HL)
(全等三角形对应角相等)
方法二:
已知:△ABC中,AB=AC 求证:∠B= C
作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
则有BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
A
B
C
D
BD=CD
方法三:
已知:△ABC中,AB=AC 求证:∠B= C
D
如图,作△ABC的中线AD
D
┌
如图, 作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
性质1:等腰三角形的两个底角相等.
( 简写成“等边对等角” )
A
B
C
在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )
已知
等边对等角
用符号语言表示为:
“等边对等角”必须在同一个等腰三角形中才成立
请注意哦!
练一练:
1、判断正误(口答)
(1) 如图,在△ABC中,
∴ ∠B=∠C.
∵ AB=BC,
C
A
B
注意使用“等边对等角”时,
边与角的对应关系.
1、判断正误(口答)
“等边对等角”只能在同一个三角形中使用.
(2) 如图,在△ABC中,
∵ AC=BC,
∴ ∠ADC=∠BEC.
C
A
B
D
E
精讲释疑例1、已知:在△ABC中,AB = AC,∠B= 80°,求∠C 和 ∠A的度数。ABC解:∵在△ABC中,AB =AC∴∠B=∠C = 80°又∵∠A + ∠ B + ∠C = 180°∴∠A = 180°- 80° - 80°= 20°2、等腰三角形一个底角为70°,它的另外
两个角为 ;
练一练:
70°
70°
40°
70°,40°
3、等腰三角形一个底角为70°,它的另外两个角为___________________;
70°,40°
70°
70°
40°
4、等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
5、等腰三角形一个角为120°,它的另外两个角为___________。
30°, 30°
等腰三角形中角的位置不明确时要分类讨论:
1.当给出的角为锐角时它可能是底角也可能是顶角
2.当给出的角是直角或钝角时它只能是顶角
作业:
1.如图, 在△ABC中, AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、 E .求证: BD = CE.
2、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
x
x
2x
2x
2x
解:∵AB=AC,BD=BC=AD
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
课堂小结
等腰三角形的性质
等边对等角
这节课我们学习了什么
等腰三角形的有关概念
匈牙利 赛格德教堂
法国巴黎 卢浮宫
埃及 金字塔
武汉长江二桥
从数学的观点去思考,这些图片都含有相同的几何图形吗?
这些三角形有什么特点?
13.3.1 等腰三角形的性质
A
B
C
1.等腰三角形:
有两条边相等的三角形
叫做等腰三角形。
等腰三角形的概念
2.相等的两条边叫做 腰
另一条边叫做 底边
底边与腰的夹角叫做底角
3.两腰所夹的角叫做顶角
腰
腰
底边
顶角
底角
自主学习
预习课本,找出什么叫等腰三角形?腰?底边?顶角?底角?
如图,把一张长方形的纸按图中虚线对折,
并剪去绿色部分,
再把它展开,得到的△ABC有什么特点
A
B
C
AB=AC
等腰三角形
活动1:剪一剪,说一说
做一做:
(1)把你们刚剪下的等腰三角形拿出来;
(2)把等腰三角形的顶角顶点记为A,底角顶点记为B、C。
(3)把等腰三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
思考:1.等腰三角形是轴对称图形吗?
2.原三角形中有哪两个角相等?
B
A
C
D
A
B
C
D
结论:
1、等腰三角形是轴对称图形
2、等腰三角形的两个底角相等
对称轴是:
底边的中线AD所在的直线
推理论证:
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
证明两个角相等有什么常见的方法:
三角形全等
如何构造两个全等的三角形?
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一:
做顶角∠BAC的平分线AD
已知:△ABC中,AB=AC求证:∠B= C
证明:
过A做AD⊥BC,垂足为D
C
A
B
D
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴∠B=∠C
∴ Rt△ABD ≌ Rt△ACD(HL)
(全等三角形对应角相等)
方法二:
已知:△ABC中,AB=AC 求证:∠B= C
作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
则有BD=CD
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)
A
B
C
D
BD=CD
方法三:
已知:△ABC中,AB=AC 求证:∠B= C
D
如图,作△ABC的中线AD
D
┌
如图, 作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
性质1:等腰三角形的两个底角相等.
( 简写成“等边对等角” )
A
B
C
在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )
已知
等边对等角
用符号语言表示为:
“等边对等角”必须在同一个等腰三角形中才成立
请注意哦!
练一练:
1、判断正误(口答)
(1) 如图,在△ABC中,
∴ ∠B=∠C.
∵ AB=BC,
C
A
B
注意使用“等边对等角”时,
边与角的对应关系.
1、判断正误(口答)
“等边对等角”只能在同一个三角形中使用.
(2) 如图,在△ABC中,
∵ AC=BC,
∴ ∠ADC=∠BEC.
C
A
B
D
E
精讲释疑例1、已知:在△ABC中,AB = AC,∠B= 80°,求∠C 和 ∠A的度数。ABC解:∵在△ABC中,AB =AC∴∠B=∠C = 80°又∵∠A + ∠ B + ∠C = 180°∴∠A = 180°- 80° - 80°= 20°2、等腰三角形一个底角为70°,它的另外
两个角为 ;
练一练:
70°
70°
40°
70°,40°
3、等腰三角形一个底角为70°,它的另外两个角为___________________;
70°,40°
70°
70°
40°
4、等腰三角形一个角为70°,它的另外两个角为___________________;
70°,40°或 55°,55°
70°
55°
55°
70°
70°
40°
5、等腰三角形一个角为120°,它的另外两个角为___________。
30°, 30°
等腰三角形中角的位置不明确时要分类讨论:
1.当给出的角为锐角时它可能是底角也可能是顶角
2.当给出的角是直角或钝角时它只能是顶角
作业:
1.如图, 在△ABC中, AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、 E .求证: BD = CE.
2、如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
x
x
2x
2x
2x
解:∵AB=AC,BD=BC=AD
∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x,
从而∠ABC= ∠C= ∠BDC=2x,
于是在△ABC中,
有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中, ∠A=36°,∠ABC=∠C=72°
课堂小结
等腰三角形的性质
等边对等角
这节课我们学习了什么
等腰三角形的有关概念
