华师大版数学八年级上册14.1.1直角三角形的三边关系 课件(共16张PPT)
文档属性
| 名称 | 华师大版数学八年级上册14.1.1直角三角形的三边关系 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
14.1.1直角三角形的三边关系(认识勾股定理)
教学目标:
1、经历勾股定理的探索过程,体会数形结合的思想。
2、理解直角三角形的三边关系,会应用勾股定理解决简单的数学问题。
3、通过对勾股定理历史的了解,感受我国的数学历史,激发学习热情。(德育目标)
教学重点:
应用勾股定理解决简单的数学问题。
教学难点:
勾股定理的探索过程以及勾股定理的验证。
2002年在北京召开的国际数学家大会。在那个大会上,到处可以看到一个简洁优美的图案在流动,那个远看像旋转的纸风车的图案就是大会的会标.
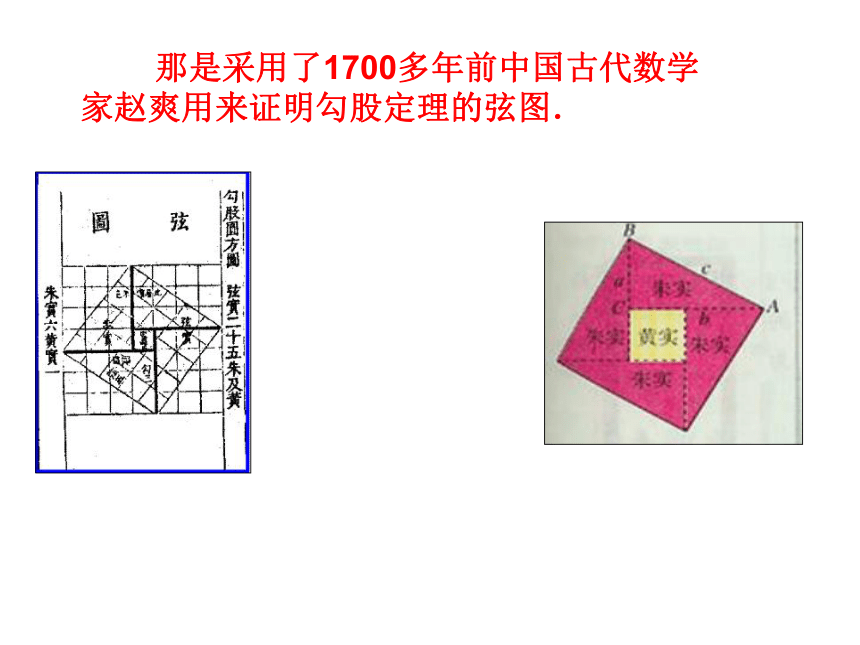
那是采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
2、直角三角形有哪些性质?
有一个角是直角;
两个锐角的和为90°(互余 )
预习导单:
1、什么是直角三角形?它的斜边、直角边分别指什么?
有一个角是直角的三角形叫直角三角形,夹直角的边叫直角边,直角的对边叫斜边。
Q
P
R
Q
P
R
A
B
C
A
B
C
预习导单:3、
P的面积(单位长度) Q的面积(单位长度) R的面积(单位长度)
左图
右图
P、Q、R面积关系 猜想直角三角形三边关系 SP+SQ=SR
BC2+AC2=AB2
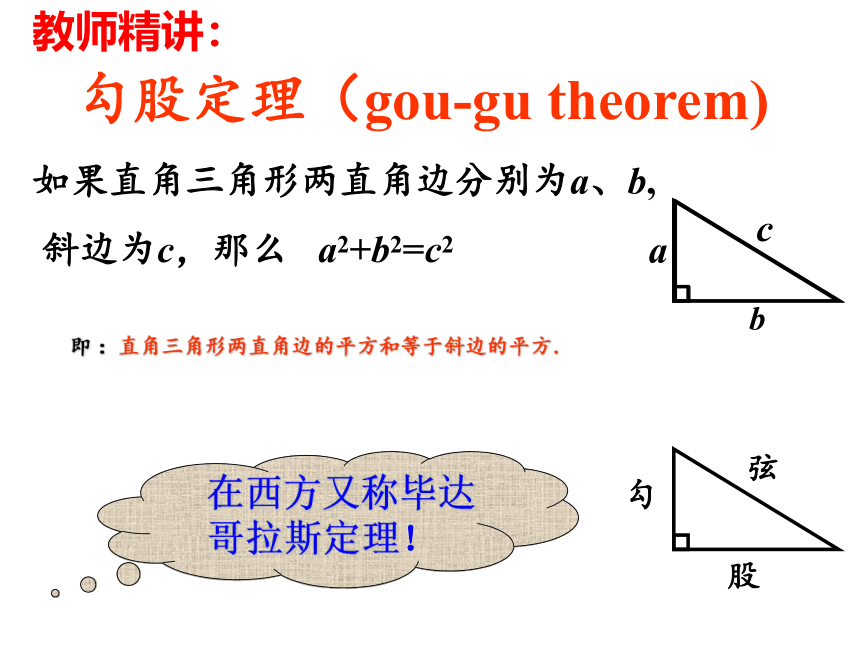
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
教师精讲:
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
证明1:
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
a
b
c
c2=a2 + b2
例1:一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
课堂练习
1、已知Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c= 10,b = 8,则a = .
③若a=2,c=6,则b= 。
2、若一个直角三角形的三边长分别为3,4, x,则x= .
3、受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c = ;
(3)若c=25,b=15,则 a = ;
2.如图,在△ABC中,∠C=90°,CD为斜边AB上的高,已知AC=12,BC=5,那么CD长为多少
C
A
B
D
家庭练习
3.图中阴影部分是一个正方形,则此正方形的面积为 .
15 cm
17 cm
4、将长为2.5米的梯子AC斜靠在墙上,底部离建筑物距离BC长为0.7米。
(1)求梯子上端A到墙的底边的垂直距离AB.
(2)现有一个同学不小心碰到梯子,使其下端C向左滑动0.8米到了C1点,问梯子的上端A下滑了多少
A
B
C
C1
A1
14.1.1直角三角形的三边关系(认识勾股定理)
教学目标:
1、经历勾股定理的探索过程,体会数形结合的思想。
2、理解直角三角形的三边关系,会应用勾股定理解决简单的数学问题。
3、通过对勾股定理历史的了解,感受我国的数学历史,激发学习热情。(德育目标)
教学重点:
应用勾股定理解决简单的数学问题。
教学难点:
勾股定理的探索过程以及勾股定理的验证。
2002年在北京召开的国际数学家大会。在那个大会上,到处可以看到一个简洁优美的图案在流动,那个远看像旋转的纸风车的图案就是大会的会标.
那是采用了1700多年前中国古代数学家赵爽用来证明勾股定理的弦图.
2、直角三角形有哪些性质?
有一个角是直角;
两个锐角的和为90°(互余 )
预习导单:
1、什么是直角三角形?它的斜边、直角边分别指什么?
有一个角是直角的三角形叫直角三角形,夹直角的边叫直角边,直角的对边叫斜边。
Q
P
R
Q
P
R
A
B
C
A
B
C
预习导单:3、
P的面积(单位长度) Q的面积(单位长度) R的面积(单位长度)
左图
右图
P、Q、R面积关系 猜想直角三角形三边关系 SP+SQ=SR
BC2+AC2=AB2
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,
斜边为c,那么 a2+b2=c2
即 :直角三角形两直角边的平方和等于斜边的平方.
a
b
c
勾
股
弦
在西方又称毕达哥拉斯定理!
教师精讲:
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
两千多年前,古希腊有个哥拉
斯学派,他们首先发现了勾股定理,因此
在国外人们通常称勾股定理为毕达哥拉斯
年希腊曾经发行了一枚纪念票。
定理。为了纪念毕达哥拉斯学派,1955
勾 股 世 界
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前,
国家之一。早在三千多年前
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
c
a
b
c
a
b
c
a
b
c
a
b
∵ c2=
=b2-2ab+a2+ 2ab
=a2+b2
∴ a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《勾股圆方图》。
证明1:
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 =
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
(a+b)2
C2
证明2:
C2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方;
a
b
c
c2=a2 + b2
例1:一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少
A
B
C
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2
=2.52-2.42
=0.49,
所以BC=0.7.
课堂练习
1、已知Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c= 10,b = 8,则a = .
③若a=2,c=6,则b= 。
2、若一个直角三角形的三边长分别为3,4, x,则x= .
3、受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
1.在△ABC中,∠C=90°.
(1)若a=6,c=10,则b= ;
(2)若a=12,b=9,则c = ;
(3)若c=25,b=15,则 a = ;
2.如图,在△ABC中,∠C=90°,CD为斜边AB上的高,已知AC=12,BC=5,那么CD长为多少
C
A
B
D
家庭练习
3.图中阴影部分是一个正方形,则此正方形的面积为 .
15 cm
17 cm
4、将长为2.5米的梯子AC斜靠在墙上,底部离建筑物距离BC长为0.7米。
(1)求梯子上端A到墙的底边的垂直距离AB.
(2)现有一个同学不小心碰到梯子,使其下端C向左滑动0.8米到了C1点,问梯子的上端A下滑了多少
A
B
C
C1
A1
