第九章 9.2.1 总体取值规律的估计 第1课时 课件(共22张PPT)
文档属性
| 名称 | 第九章 9.2.1 总体取值规律的估计 第1课时 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 09:11:16 | ||
图片预览








文档简介
(共22张PPT)
第九章
9.2.1 总体取值规律的估计 第1课时
人教A版(2019)
教学目标
学习目标 数学素养
1.掌握频率分布表的作法以及频率分布直方图的画法. 1.数据分析素养.
2.会利用频率分布表、频率分布直方图对数据进行可视化描述. 2.数据分析素养和运算素养.
知新引入
收集数据是为了寻找数据中蕴含的信息.因为实际问题中数据多而杂乱,往往无法直接从原始数据中发现规律,所以需要根据问题的背景特点,选择合适的统计图表对数据进行整理和直观描述.在此基础上,通过数据分析,找出数据中蕴含的信息,就可以用这些信息来解决实际问题了.
面对一个统计问题,在随机抽样获得观测数据的基础上,需要根据分析数据的需要,选择适当的统计图表描述和表示数据,获得样本的规律,并利用样本的规律估计 总体的规律,解决相应的实际问题.请看下面的问题.
下面我们讨论对随机抽样获取的数据的处理方法.
9.2.1 总体取值规律的估计
知新探究
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过的部分按平价收费,超出的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
知新探究
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过的部分按平价收费,超出的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
每户居民月均用水量标准如果定得太低,会影响很多居民的日常生活;如果标准太高,则不利于节约用水.为了确定一个较为合理的用水标准,必须先了解在全市所有居民中,月用水量在不同范围内的居民用户所占的比例情况.
如果经费、时间等条件允许,我们可以通过全面调查获得过去一年全市所有居民用户的月均用水量数据,进而得到月均用水量在不同范围内的居民用户所占的比例.由于全市居民用户很多,通常采用抽样调查的方式.通过分析样本观测数据,来估计全市居民用户月均用水量的分布情况.
在这个问题中,总体是该市全体居民用户,个体是每户居民用户,调查的变量是居民用户的月均用水量.
知新探究
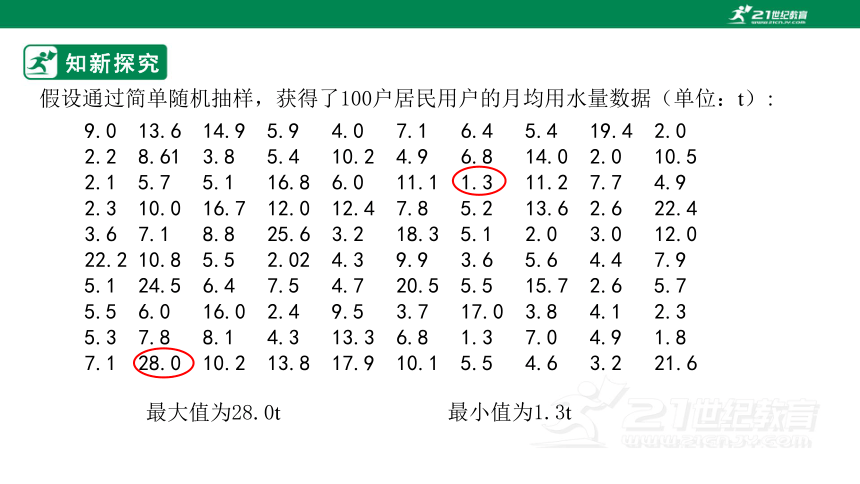
假设通过简单随机抽样,获得了100户居民用户的月均用水量数据(单位:t):
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.61 3.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.02 4.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
最大值为28.0t
最小值为1.3t
知新探究
从这组数据我们能发现什么信息
如果将这组数据从小到大排序,这组数据的最小值是1.3t,最大值是28.0t,其他在1.3t到28.0t之间,为了更深入地挖掘数据蕴含的信息,需要对数据作进一步的整理与分析.
为了探索一组数据的取值规律,一般要采用表格对数据进行整理,或者用图将数据直观表示出来.在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
用表格整理数据是通过改变数据的组织方式,为数据的解释提供新的方式.用图表示数据不仅有利于从数据中提取信息,还可以利用图形传递信息.
在这个实际问题中,因为我们更关心月均用水量在不
同范围内的居民占全市居民用户的比例,所以选择频率分
布表(frequency distribution table)和频率分布直方
图(frequency distribution hastogram)来整理和表示数据.与画频数分布直方图类似,我们可以按以下步骤制作频率分布表、频率分布直方图.
知新探究
1.求极差
极差是一组数据中最大值与最小值的差.样本观测数据的最小值是1.3t,最大值是28.0t,极差为 28.0-1.3=26.7. 这说明样本观测数据的变化范围是26.7t.
2.决定组距和组数
合适的组距与组数对发现数据分布规律有重要意义.组数太多或太少,都会影响我们了解数据的分布情况.组距和组数的确定没有固定标准,常常需要一个选择和尝试的过程.数据分组的组数与数据的个数有关,一般数据的个数越多,所分的组数越多.当样本量不超过100时,常分成5~12组.为了方便起见,一般取等长组距,并且组距应力求“取整”.
数据分组可以是等距的,也可以是不等距的,要根据数据的特点而定.有时为了方便,往往按等距分组,或者除了第一和最后的两段,其他各段按等距分组.
分析时可以先确定组距,也可以先确定组数.如果我们确定组距为3,则
.
即可以将数据分为9组,这样也说明这个组距是比较合适的.
知新探究
3.将数据分组
由于组距为3,9个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值.例如,可以取区间为[1.2,28.2],按如下方式把样本观测数据以组距3分为9组:
[1.2,4.2),[4.2,7.2),… ,[25.2,28.2].
通常对组内数据所在区间:左闭右开,最后一组取闭区间.
知新探究
4.列频率分布表
统计频数,计算各小组频率.
.
例如第一小组的频率是
=0.23.
作出频率分布表.
新知探究
5.画频率分布直方图
在直角坐标系中,用横轴表示月均用水量,纵轴表示.
这里,实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的疏密程度.
月均用水量/t
0.077
频率/组距
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0
0.02
0.08
0.1
0.06
0.04
4.2
1.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
小长方形的面积=组距×=频率
频率分布直方图就以面积的形式反映数据落在各小组的频率的大小.
利用统计软件,可以快速准确低画出频率分布直方图,频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.
在频率分布直方图中,各小长方形面积的总和等于1.
新知探究
观察频率分布表和频率分布直方图,这组数据中蕴含了哪些有用的信息?试用适当的语言描述居民用户月均用水量的分布规律.
从频率分布表中可以看出,样本观测数据落在各个小组的比例大小.例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小.
从频率分布直方图能直观地表明数据分布的形状和总体趋势.大部分居民用户的月均用水量集中在一个较低值区域,尤其在[1.2,7.2)最为集中,少数用户居民的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
新知探究
绘制频率分布直方图的步骤
1.求极差
一组数据中最大值与最小值的差
2.决定组距和组数
组数若则组数若则组数为不小于的最小整数
3.将数据分组
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
4.列频率分布表
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
5.画频率分布直方图
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
有了样本观测数据的频率分布,可以用它估计总体的取值规律.根据100户居民用户月均用水量的频率分布,可以推测出该市全体居民用户月均用水量集中在较低区域.这使确定用水标准时,可以定一个合适的值,以达到既不影响大多数居民用户的水费支出,又能节水的目的.需要注意的是,由于样本的随机性,这种估计可能存在一定误差,但这一误差一般不会影响对总体分布情况的大致了解.
新知探究
分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分布直方图.观察图形,不同的组数对于直方图呈现数据分布规律有什么影响
①组数为3
①组数为27
由图中可以看出,同一组数据,组数不同,得到的直方图形状不尽相同.
新知探究
①组数为3
图①中直方图的组数少、组距大,从图中容易看出,数据分布的整体规律是随着月均用水量的增加,居民用户数的频率在降低,而月均用水量在区间[1.2,10.2)内的居民用户数的频率,远大于在另两个区间[10.2,19.2)和[19.2,28.2]内的频率,这说明大部分居民用户的月均用水量都少有10.2t.
从上述分析可以看出,当直方图的组数少、组距大时,容易看出数据的整体分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原始数据信息.
新知探究
②组数为27
图②中直方图的组数多、组距小,从图中容易看出,数据主要集中在低值取,尤其在[5.2,6.2)内最为集中.从总体上看,随着月均用水量的增加 ,居民用户数的频率呈现下降趋势,但存在个别区间变大或缺失的情况.
从上述分析可以看出,当直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得不规则,不容易看出总体数据的分布特点.
这里再次指出,对于同一组数据,因为组距、组数不同而得到不同形状的直方图,会给人以不同的频率分布印象,这种印象有时会影响人们对总体的判断.因此,要注意积累数据分组、合理用图表的经验.
初试身手
1.判断下列叙述是否正确?正确的打“√”,错误的打“×”.
⑴在频率分布直方图中得不到原始的数据内容,把数据表示成直方图后原有的具体数据信息就被抹掉了 . ( )
⑵在频率分布直方图中,纵轴表示频率. ( )
⑶在频率分布直方图中,各小长方形的面积为1. ( )
⑷在频率分布直方图中,各小长方形的面积之比等于各组频率之比. ( )
×
√
√
×
课堂小结
绘制频率分布直方图的步骤
1.求极差
一组数据中最大值与最小值的差
2.决定组距和组数
组数若则组数若则组数为不小于的最小整数
3.将数据分组
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
4.列频率分布表
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
5.画频率分布直方图
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
作业布置
作业: P198 练习 第1,2,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第九章
9.2.1 总体取值规律的估计 第1课时
人教A版(2019)
教学目标
学习目标 数学素养
1.掌握频率分布表的作法以及频率分布直方图的画法. 1.数据分析素养.
2.会利用频率分布表、频率分布直方图对数据进行可视化描述. 2.数据分析素养和运算素养.
知新引入
收集数据是为了寻找数据中蕴含的信息.因为实际问题中数据多而杂乱,往往无法直接从原始数据中发现规律,所以需要根据问题的背景特点,选择合适的统计图表对数据进行整理和直观描述.在此基础上,通过数据分析,找出数据中蕴含的信息,就可以用这些信息来解决实际问题了.
面对一个统计问题,在随机抽样获得观测数据的基础上,需要根据分析数据的需要,选择适当的统计图表描述和表示数据,获得样本的规律,并利用样本的规律估计 总体的规律,解决相应的实际问题.请看下面的问题.
下面我们讨论对随机抽样获取的数据的处理方法.
9.2.1 总体取值规律的估计
知新探究
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过的部分按平价收费,超出的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
知新探究
问题1:我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市政府为了减少水资源的浪费,计划对居民生活用水费用实施阶梯式水价制度,即确定一户居民月均用水量标准a,用水量不超过的部分按平价收费,超出的部分按议价收费,如果希望确定一个比较合理的标准,以使大部分居民用户的水费支出不受影响,你认为需要做哪些工作?
每户居民月均用水量标准如果定得太低,会影响很多居民的日常生活;如果标准太高,则不利于节约用水.为了确定一个较为合理的用水标准,必须先了解在全市所有居民中,月用水量在不同范围内的居民用户所占的比例情况.
如果经费、时间等条件允许,我们可以通过全面调查获得过去一年全市所有居民用户的月均用水量数据,进而得到月均用水量在不同范围内的居民用户所占的比例.由于全市居民用户很多,通常采用抽样调查的方式.通过分析样本观测数据,来估计全市居民用户月均用水量的分布情况.
在这个问题中,总体是该市全体居民用户,个体是每户居民用户,调查的变量是居民用户的月均用水量.
知新探究
假设通过简单随机抽样,获得了100户居民用户的月均用水量数据(单位:t):
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.61 3.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.02 4.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
最大值为28.0t
最小值为1.3t
知新探究
从这组数据我们能发现什么信息
如果将这组数据从小到大排序,这组数据的最小值是1.3t,最大值是28.0t,其他在1.3t到28.0t之间,为了更深入地挖掘数据蕴含的信息,需要对数据作进一步的整理与分析.
为了探索一组数据的取值规律,一般要采用表格对数据进行整理,或者用图将数据直观表示出来.在初中,我们曾用频数分布表和频数分布图来整理和表示这种数值型数据,由此能使我们清楚地知道数据分布在各个小组的个数.
用表格整理数据是通过改变数据的组织方式,为数据的解释提供新的方式.用图表示数据不仅有利于从数据中提取信息,还可以利用图形传递信息.
在这个实际问题中,因为我们更关心月均用水量在不
同范围内的居民占全市居民用户的比例,所以选择频率分
布表(frequency distribution table)和频率分布直方
图(frequency distribution hastogram)来整理和表示数据.与画频数分布直方图类似,我们可以按以下步骤制作频率分布表、频率分布直方图.
知新探究
1.求极差
极差是一组数据中最大值与最小值的差.样本观测数据的最小值是1.3t,最大值是28.0t,极差为 28.0-1.3=26.7. 这说明样本观测数据的变化范围是26.7t.
2.决定组距和组数
合适的组距与组数对发现数据分布规律有重要意义.组数太多或太少,都会影响我们了解数据的分布情况.组距和组数的确定没有固定标准,常常需要一个选择和尝试的过程.数据分组的组数与数据的个数有关,一般数据的个数越多,所分的组数越多.当样本量不超过100时,常分成5~12组.为了方便起见,一般取等长组距,并且组距应力求“取整”.
数据分组可以是等距的,也可以是不等距的,要根据数据的特点而定.有时为了方便,往往按等距分组,或者除了第一和最后的两段,其他各段按等距分组.
分析时可以先确定组距,也可以先确定组数.如果我们确定组距为3,则
.
即可以将数据分为9组,这样也说明这个组距是比较合适的.
知新探究
3.将数据分组
由于组距为3,9个组距的长度超过极差,我们可以使第一组的左端点略小于数据中的最小值,最后一组的右端点略大于数据中的最大值.例如,可以取区间为[1.2,28.2],按如下方式把样本观测数据以组距3分为9组:
[1.2,4.2),[4.2,7.2),… ,[25.2,28.2].
通常对组内数据所在区间:左闭右开,最后一组取闭区间.
知新探究
4.列频率分布表
统计频数,计算各小组频率.
.
例如第一小组的频率是
=0.23.
作出频率分布表.
新知探究
5.画频率分布直方图
在直角坐标系中,用横轴表示月均用水量,纵轴表示.
这里,实际上就是频率分布直方图中各小长方形的高度,它反映了各组样本观测数据的疏密程度.
月均用水量/t
0.077
频率/组距
0.107
0.043
0.030
0.030
0.017
0.010
0.013
0.007
0
0.02
0.08
0.1
0.06
0.04
4.2
1.2
7.2
10.2
13.2
16.2
19.2
22.2
25.2
28.2
小长方形的面积=组距×=频率
频率分布直方图就以面积的形式反映数据落在各小组的频率的大小.
利用统计软件,可以快速准确低画出频率分布直方图,频率分布直方图把样本数据落在各小组的比例大小直观化,更有利于我们从整体上把握数据分布的特点.
在频率分布直方图中,各小长方形面积的总和等于1.
新知探究
观察频率分布表和频率分布直方图,这组数据中蕴含了哪些有用的信息?试用适当的语言描述居民用户月均用水量的分布规律.
从频率分布表中可以看出,样本观测数据落在各个小组的比例大小.例如,月均用水量在区间[4.2,7.2)内的居民用户最多,在区间[1.2,4.2)内的次之,而月均用水量超过16.2的各区间内数据所占比例较小.
从频率分布直方图能直观地表明数据分布的形状和总体趋势.大部分居民用户的月均用水量集中在一个较低值区域,尤其在[1.2,7.2)最为集中,少数用户居民的月均用水量偏多,而且随着月均用水量的增加,居民用户数呈现降低趋势.
新知探究
绘制频率分布直方图的步骤
1.求极差
一组数据中最大值与最小值的差
2.决定组距和组数
组数若则组数若则组数为不小于的最小整数
3.将数据分组
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
4.列频率分布表
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
5.画频率分布直方图
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
有了样本观测数据的频率分布,可以用它估计总体的取值规律.根据100户居民用户月均用水量的频率分布,可以推测出该市全体居民用户月均用水量集中在较低区域.这使确定用水标准时,可以定一个合适的值,以达到既不影响大多数居民用户的水费支出,又能节水的目的.需要注意的是,由于样本的随机性,这种估计可能存在一定误差,但这一误差一般不会影响对总体分布情况的大致了解.
新知探究
分别以3和27为组数,对数据进行等距分组,画出100户居民用户月均用水量的频率分布直方图.观察图形,不同的组数对于直方图呈现数据分布规律有什么影响
①组数为3
①组数为27
由图中可以看出,同一组数据,组数不同,得到的直方图形状不尽相同.
新知探究
①组数为3
图①中直方图的组数少、组距大,从图中容易看出,数据分布的整体规律是随着月均用水量的增加,居民用户数的频率在降低,而月均用水量在区间[1.2,10.2)内的居民用户数的频率,远大于在另两个区间[10.2,19.2)和[19.2,28.2]内的频率,这说明大部分居民用户的月均用水量都少有10.2t.
从上述分析可以看出,当直方图的组数少、组距大时,容易看出数据的整体分布特点,但由于无法看出每组内的数据分布情况,损失了较多的原始数据信息.
新知探究
②组数为27
图②中直方图的组数多、组距小,从图中容易看出,数据主要集中在低值取,尤其在[5.2,6.2)内最为集中.从总体上看,随着月均用水量的增加 ,居民用户数的频率呈现下降趋势,但存在个别区间变大或缺失的情况.
从上述分析可以看出,当直方图的组数多、组距小时,保留了较多的原始数据信息,但由于小长方形较多,有时图形会变得不规则,不容易看出总体数据的分布特点.
这里再次指出,对于同一组数据,因为组距、组数不同而得到不同形状的直方图,会给人以不同的频率分布印象,这种印象有时会影响人们对总体的判断.因此,要注意积累数据分组、合理用图表的经验.
初试身手
1.判断下列叙述是否正确?正确的打“√”,错误的打“×”.
⑴在频率分布直方图中得不到原始的数据内容,把数据表示成直方图后原有的具体数据信息就被抹掉了 . ( )
⑵在频率分布直方图中,纵轴表示频率. ( )
⑶在频率分布直方图中,各小长方形的面积为1. ( )
⑷在频率分布直方图中,各小长方形的面积之比等于各组频率之比. ( )
×
√
√
×
课堂小结
绘制频率分布直方图的步骤
1.求极差
一组数据中最大值与最小值的差
2.决定组距和组数
组数若则组数若则组数为不小于的最小整数
3.将数据分组
通常对组内数值所在的区间取左闭右开区间,最后一组取闭区间
4.列频率分布表
一般分4列:分组、频数累计、频数、频率,最后一行是合计,其中频数合计应是样本量,频率合计应是1.00
5.画频率分布直方图
在频率分布直方图中,纵轴表示频率与组距的比值,数据落在各小组内的频率用各小长方形的面积来表示,各小长方形的面积和是1
作业布置
作业: P198 练习 第1,2,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
