河北省邢台市信都区2023-2024学年八年级下学期月考数学试题(含答案)
文档属性
| 名称 | 河北省邢台市信都区2023-2024学年八年级下学期月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 842.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 14:00:01 | ||
图片预览



文档简介
2023—2024学年第二学期期中考试
八年级数学试题(冀教版)
考试范围:18-21.3章
说明:
1. 本试题共6页,总分120分.
2. 请将所有答案涂写在答题卡上,答在试卷上无效.
一、选择题(本大题共14个小题,共38分,1~10小题每小题3分,11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 在一次函数中,k的值是( )
A. 1 B. 2 C. -1 D. -2
2. 学校召开运动会,30名学生要统一购买运动鞋,需要的数据是( )
A. 每个学生喜欢的牌子 B. 一部分学生鞋的码数
C. 每个学生的身高 D. 每个学生鞋的码数
3. 下列各点中,位于第三象限的是( )
A. B. C. D.
4. 某校为了解学生喜爱的体育运动项目,筹备体育活动,设计了不完整的调查问卷:准备在“①室外体育运动,②篮球,③实心球,④跳绳,⑤球类运动”中选取3个作为该调查问卷的备选项目,你认为合理的是( )
A. ①②③ B. ①③⑤ C. ②④⑤ D. ②③④
5. 函数中自变量x的取值范围是( )
A. B. C. D.
6. 将第一象限的“小旗”各点的横坐标分别乘以-1,纵坐标保持不变,符合上述要求的图形是( )
A. B. C. D.
7. 要调查下列两个问题:
①了解班级同学中哪个月份出生的人数最多;
②了解全市七年级学生早餐是否有喝牛奶的习惯.
说法正确的是( )
A. ①是普查,②是抽样调查 B. ①是抽样调查,②是普查
C. ①、②均是普查 D. ①、②均是抽样调查
8. 对于甲、乙两条折线、说法正确的是( )
A. 甲表示y是x的函数,乙不能表示y是x的函数
B. 甲、乙均不能表示y是x的函数
C. 甲、乙均表示y是x的函数
D. 甲不能表示y是x的函数,乙表示y是x的函数
9. 为了解某校2000名学生每周参加社团活动时间的情况,随机抽查了100名学生的社团活动时间进行统计,并绘制成如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),下列说法错误的是( )
A. 整理数据时按时间分成了五组,组距是2
B. 100名学生每周的社团活动时间是总体的一个样本
C. 2000名学生是总体
D. 抽取的学生中,每周参加社团活动的时间在6~8小时之间的学生人数最多
10. 如图,在一次活动中,位于A处的嘉嘉准备前往相距10m的B处与琪琪会合.请你用方向和距离描述嘉嘉相对于琪琪的位置,其中描述正确的是( )
A. 嘉嘉在琪琪的北偏东,10m处 B. 嘉嘉在琪琪的北偏东,10m处
C. 嘉嘉在琪琪的南偏西,10m处 D. 嘉嘉在琪琪的南偏西,10m处
11. 在平面直角坐标系中,将线段AB向左平移3个单位长度,再向下平移2个单位长度后,得到如图所示的线段,线段的中点N的坐标如图,则平移前线段AB的中点的坐标是( )
A. B. C. D.
12. 已知点和点均在一次函数的图象上,且,则a的值可能是( )
A. 3 B. 0 C. -1 D. -2
13. 已知,,,,若,则a的值是( )
A. -4 B. -2 C. 4 D. 8
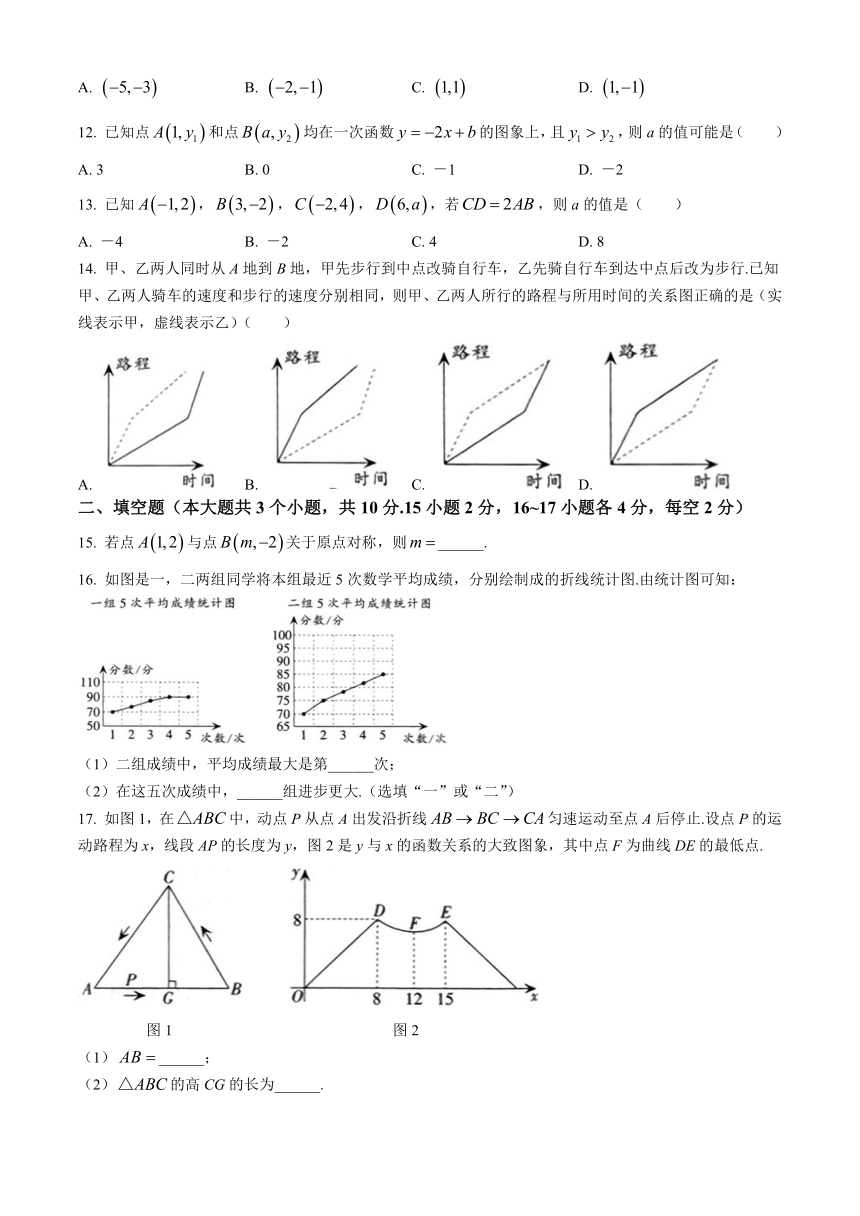
14. 甲、乙两人同时从A地到B地,甲先步行到中点改骑自行车,乙先骑自行车到达中点后改为步行.已知甲、乙两人骑车的速度和步行的速度分别相同,则甲、乙两人所行的路程与所用时间的关系图正确的是(实线表示甲,虚线表示乙)( )
A. B. C. D.
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
15. 若点与点关于原点对称,则______.
16. 如图是一,二两组同学将本组最近5次数学平均成绩,分别绘制成的折线统计图.由统计图可知:
(1)二组成绩中,平均成绩最大是第______次;
(2)在这五次成绩中,______组进步更大.(选填“一”或“二”)
17. 如图1,在中,动点P从点A出发沿折线匀速运动至点A后停止.设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中点F为曲线DE的最低点.
图1 图2
(1)______;
(2)的高CG的长为______.
三、解答题(本大题共七个小题,满分72分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)
在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?
(2)不挂重物时,弹簧长是多少?
19.(本小题满分9分)
为让每个农村孩子都能上学,国家实施了“农村中小学寄宿制学校建设工程”,如图是某寄宿制学校的平面示意图,已知旗杆的位置是,实验室的位置是.
(1)请你画出该学校平面示意图所在的坐标系;
(2)办公楼的位置是,教学楼的位置是,在图中标出办公楼和教学楼的位置;
(3)写出食堂、图书馆的坐标
20.(本小题满分9分)
如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.
(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式;
(2)求的值.
21.(本小题满分10分)
【调查统计】某学校计划某天同时开展四项竞赛,分别是A. 法律知识竞赛;B. 国际象棋大赛;C. 花样剪纸大赛;D. 创意书签设计大赛.要求每位同学必须参加且只能选一项,最后把统计结果绘制成了两幅统计图,请根据图中提供的信息回答以下问题:
(1)求共调查了多少名学生?求选择“D”学生的人数,并补全条形统计图;
(2)求扇形统计图中“创意书签设计大赛”部分所对应的圆心角度数是多少度?
【解决问题】该学校有1000名学生参加本次活动,地点安排在两个多功能厅,每场报告时间为60分钟.由下面的活动日程表可知,A和C两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下,请你根据调查结果,补全此次活动日程表,并说明理由.
“学科月活动”主题日活动日程表
地点(座位数)时间 1号多功能厅(200座) 2号多功能厅(400座)
13:00—14:00 A
15:00—16:00 C
22.(本小题满分10分)
如图,在平面直角坐标系中,点,,,过点C作直线与y轴相交于D点.
(1)当k满足什么条件时,函数y的值随x的值的增大而增大;
(2)求的面积;
(3)若点A和点B在直线的两侧,求k的取值范围.
23.(本小题满分12分)
一只蚂蚁在一个半圆形花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:线段OA、半圆弧AB、线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示.(注:圆周率的值取3)
图1 图2
(1)请直接写出:花坛的半径是______米,蚂蚁爬行的速度为______米/分;
(2)计算图中的a值;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②求蚂蚁从点O出发到返回O点的时间.
24.(本小题满分13分)
在平面直角坐标系中,已知直线:与y轴相交于A点,与直线:相交于点.
(1)求m、k的值;
(2)求AM的长;
(3)若直线与直线,及x轴有3个不同的交点,且其中两点关于第三点对称,求a的值.
2023-2024学年第二学期期中考试
八年级数学试题参考答案(冀教版)
1-5 DDBDB 6-10 CAACB 11-14 CAAC
15. -1 16.(1)5,(2)一 17.(1)8 (2)
18.(1)反映了弹簧长度y与所挂物体质量x之间的关系…………………………6分
(2)20cm……………………………………………………………………………………9分
19. 解:(1)如图所示:
(2)如图所示:
(3)食堂,图书馆.………………………………………9分
20. 解:(1)设一次函数解析式为,点,在直线解析式上,
,解得,函数解析式为:;…………………………5分
(2)在函数中,当时,;当时,,
∴……………………………………………………………………9分
21.【调查统计】
解:(1)共调查的学生人数为(人),………………2分
D类型的人数为(人),…………………………………4分
补全条形统计图如下:
……………………………………………………6分
(2),
答:扇形统计图中“创意书签设计大赛”部分所对应的圆心角度数是72度;……8分
【解决问题】
喜欢B类型的人数(人),
“学科月活动”主题日活动日程表
地点(座位数)时间 1号多功能厅(200座) 2号多功能厅(400座)
13:00-14:00 A B
15:00-16:00 D C
喜欢D类型的人数为(人),补全此次活动日程表如下:
……………………………………………………………………………………………10分
解:(1)当时,函数y的值随x的值的增大而增大
解得,…………………………………………………………………………3分
(2)∵,,∴,
∵,∴C点到AB所在直线的距离为,
∴的面积=……………………………………………………6分
(3)当直线经过点时,,解之得,;
当直线经过点时,,解得,,
∴点A和点B在直线的两侧时,k的取值范围为…………10分
23.(1)4,2;……………………………………………………………………………2分
(2)由题意得:;…………………………………………4分
(3)①∵沿途只有一处食物,∴蚂蚁只能在BO段吃食物,,
∴蚂蚁从B爬1分钟找到食物,(米),
∴蚂蚁停下来吃食的地方距出发点2米;……………………………………………10分
②∵蚂蚁停下来吃食的地方距出发点2米,(分钟),(分钟),
∴蚂蚁返回O的时间为12分钟………………………………………………………12分
24. 解:(1)∵点在直线上,∴,∴,
∴,∵点在上,∴,∴…………………4分
(2)∵已知直线:与y轴相交于A点,∴,
∴,过M点作轴,∴,∴,,
∴,∴…………………………………………7分
(3)把代入得,,
把代入得,,
分三种情况:①当第三点在直线上时,,解得;
②当第三点在直线上时,,解得;
③当第三点在x轴上时,则,解得,
∴直线与直线,及x轴有3个不同的交点,且其中两点关于第三点对称,则a的值为或或13……………………………………………………………13分
八年级数学试题(冀教版)
考试范围:18-21.3章
说明:
1. 本试题共6页,总分120分.
2. 请将所有答案涂写在答题卡上,答在试卷上无效.
一、选择题(本大题共14个小题,共38分,1~10小题每小题3分,11~14小题各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 在一次函数中,k的值是( )
A. 1 B. 2 C. -1 D. -2
2. 学校召开运动会,30名学生要统一购买运动鞋,需要的数据是( )
A. 每个学生喜欢的牌子 B. 一部分学生鞋的码数
C. 每个学生的身高 D. 每个学生鞋的码数
3. 下列各点中,位于第三象限的是( )
A. B. C. D.
4. 某校为了解学生喜爱的体育运动项目,筹备体育活动,设计了不完整的调查问卷:准备在“①室外体育运动,②篮球,③实心球,④跳绳,⑤球类运动”中选取3个作为该调查问卷的备选项目,你认为合理的是( )
A. ①②③ B. ①③⑤ C. ②④⑤ D. ②③④
5. 函数中自变量x的取值范围是( )
A. B. C. D.
6. 将第一象限的“小旗”各点的横坐标分别乘以-1,纵坐标保持不变,符合上述要求的图形是( )
A. B. C. D.
7. 要调查下列两个问题:
①了解班级同学中哪个月份出生的人数最多;
②了解全市七年级学生早餐是否有喝牛奶的习惯.
说法正确的是( )
A. ①是普查,②是抽样调查 B. ①是抽样调查,②是普查
C. ①、②均是普查 D. ①、②均是抽样调查
8. 对于甲、乙两条折线、说法正确的是( )
A. 甲表示y是x的函数,乙不能表示y是x的函数
B. 甲、乙均不能表示y是x的函数
C. 甲、乙均表示y是x的函数
D. 甲不能表示y是x的函数,乙表示y是x的函数
9. 为了解某校2000名学生每周参加社团活动时间的情况,随机抽查了100名学生的社团活动时间进行统计,并绘制成如图所示的频数分布直方图(每一组含前一个边界值,不含后一个边界值),下列说法错误的是( )
A. 整理数据时按时间分成了五组,组距是2
B. 100名学生每周的社团活动时间是总体的一个样本
C. 2000名学生是总体
D. 抽取的学生中,每周参加社团活动的时间在6~8小时之间的学生人数最多
10. 如图,在一次活动中,位于A处的嘉嘉准备前往相距10m的B处与琪琪会合.请你用方向和距离描述嘉嘉相对于琪琪的位置,其中描述正确的是( )
A. 嘉嘉在琪琪的北偏东,10m处 B. 嘉嘉在琪琪的北偏东,10m处
C. 嘉嘉在琪琪的南偏西,10m处 D. 嘉嘉在琪琪的南偏西,10m处
11. 在平面直角坐标系中,将线段AB向左平移3个单位长度,再向下平移2个单位长度后,得到如图所示的线段,线段的中点N的坐标如图,则平移前线段AB的中点的坐标是( )
A. B. C. D.
12. 已知点和点均在一次函数的图象上,且,则a的值可能是( )
A. 3 B. 0 C. -1 D. -2
13. 已知,,,,若,则a的值是( )
A. -4 B. -2 C. 4 D. 8
14. 甲、乙两人同时从A地到B地,甲先步行到中点改骑自行车,乙先骑自行车到达中点后改为步行.已知甲、乙两人骑车的速度和步行的速度分别相同,则甲、乙两人所行的路程与所用时间的关系图正确的是(实线表示甲,虚线表示乙)( )
A. B. C. D.
二、填空题(本大题共3个小题,共10分.15小题2分,16~17小题各4分,每空2分)
15. 若点与点关于原点对称,则______.
16. 如图是一,二两组同学将本组最近5次数学平均成绩,分别绘制成的折线统计图.由统计图可知:
(1)二组成绩中,平均成绩最大是第______次;
(2)在这五次成绩中,______组进步更大.(选填“一”或“二”)
17. 如图1,在中,动点P从点A出发沿折线匀速运动至点A后停止.设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中点F为曲线DE的最低点.
图1 图2
(1)______;
(2)的高CG的长为______.
三、解答题(本大题共七个小题,满分72分,解答题应写出必要的解题步骤或文字说明)
18.(本小题满分9分)
在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂物体的质量x/kg 0 1 2 3 4 5
弹簧的长度y/cm 20 22 24 26 28 30
(1)上表反映了哪两个变量之间的关系?
(2)不挂重物时,弹簧长是多少?
19.(本小题满分9分)
为让每个农村孩子都能上学,国家实施了“农村中小学寄宿制学校建设工程”,如图是某寄宿制学校的平面示意图,已知旗杆的位置是,实验室的位置是.
(1)请你画出该学校平面示意图所在的坐标系;
(2)办公楼的位置是,教学楼的位置是,在图中标出办公楼和教学楼的位置;
(3)写出食堂、图书馆的坐标
20.(本小题满分9分)
如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.
(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式;
(2)求的值.
21.(本小题满分10分)
【调查统计】某学校计划某天同时开展四项竞赛,分别是A. 法律知识竞赛;B. 国际象棋大赛;C. 花样剪纸大赛;D. 创意书签设计大赛.要求每位同学必须参加且只能选一项,最后把统计结果绘制成了两幅统计图,请根据图中提供的信息回答以下问题:
(1)求共调查了多少名学生?求选择“D”学生的人数,并补全条形统计图;
(2)求扇形统计图中“创意书签设计大赛”部分所对应的圆心角度数是多少度?
【解决问题】该学校有1000名学生参加本次活动,地点安排在两个多功能厅,每场报告时间为60分钟.由下面的活动日程表可知,A和C两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下,请你根据调查结果,补全此次活动日程表,并说明理由.
“学科月活动”主题日活动日程表
地点(座位数)时间 1号多功能厅(200座) 2号多功能厅(400座)
13:00—14:00 A
15:00—16:00 C
22.(本小题满分10分)
如图,在平面直角坐标系中,点,,,过点C作直线与y轴相交于D点.
(1)当k满足什么条件时,函数y的值随x的值的增大而增大;
(2)求的面积;
(3)若点A和点B在直线的两侧,求k的取值范围.
23.(本小题满分12分)
一只蚂蚁在一个半圆形花坛的周边寻找食物,如图1,蚂蚁从圆心O出发,按图中箭头所示的方向,依次匀速爬完下列三条线路:线段OA、半圆弧AB、线段BO后,回到出发点.蚂蚁离出发点的距离S(蚂蚁所在位置与O点之间线段的长度)与时间t之间的图象如图2所示.(注:圆周率的值取3)
图1 图2
(1)请直接写出:花坛的半径是______米,蚂蚁爬行的速度为______米/分;
(2)计算图中的a值;
(3)若沿途只有一处有食物,蚂蚁在寻找到食物后停下来吃了2分钟,并知蚂蚁在吃食物的前后,始终保持爬行且爬行速度不变,请你求出:
①蚂蚁停下来吃食物的地方离出发点的距离;
②求蚂蚁从点O出发到返回O点的时间.
24.(本小题满分13分)
在平面直角坐标系中,已知直线:与y轴相交于A点,与直线:相交于点.
(1)求m、k的值;
(2)求AM的长;
(3)若直线与直线,及x轴有3个不同的交点,且其中两点关于第三点对称,求a的值.
2023-2024学年第二学期期中考试
八年级数学试题参考答案(冀教版)
1-5 DDBDB 6-10 CAACB 11-14 CAAC
15. -1 16.(1)5,(2)一 17.(1)8 (2)
18.(1)反映了弹簧长度y与所挂物体质量x之间的关系…………………………6分
(2)20cm……………………………………………………………………………………9分
19. 解:(1)如图所示:
(2)如图所示:
(3)食堂,图书馆.………………………………………9分
20. 解:(1)设一次函数解析式为,点,在直线解析式上,
,解得,函数解析式为:;…………………………5分
(2)在函数中,当时,;当时,,
∴……………………………………………………………………9分
21.【调查统计】
解:(1)共调查的学生人数为(人),………………2分
D类型的人数为(人),…………………………………4分
补全条形统计图如下:
……………………………………………………6分
(2),
答:扇形统计图中“创意书签设计大赛”部分所对应的圆心角度数是72度;……8分
【解决问题】
喜欢B类型的人数(人),
“学科月活动”主题日活动日程表
地点(座位数)时间 1号多功能厅(200座) 2号多功能厅(400座)
13:00-14:00 A B
15:00-16:00 D C
喜欢D类型的人数为(人),补全此次活动日程表如下:
……………………………………………………………………………………………10分
解:(1)当时,函数y的值随x的值的增大而增大
解得,…………………………………………………………………………3分
(2)∵,,∴,
∵,∴C点到AB所在直线的距离为,
∴的面积=……………………………………………………6分
(3)当直线经过点时,,解之得,;
当直线经过点时,,解得,,
∴点A和点B在直线的两侧时,k的取值范围为…………10分
23.(1)4,2;……………………………………………………………………………2分
(2)由题意得:;…………………………………………4分
(3)①∵沿途只有一处食物,∴蚂蚁只能在BO段吃食物,,
∴蚂蚁从B爬1分钟找到食物,(米),
∴蚂蚁停下来吃食的地方距出发点2米;……………………………………………10分
②∵蚂蚁停下来吃食的地方距出发点2米,(分钟),(分钟),
∴蚂蚁返回O的时间为12分钟………………………………………………………12分
24. 解:(1)∵点在直线上,∴,∴,
∴,∵点在上,∴,∴…………………4分
(2)∵已知直线:与y轴相交于A点,∴,
∴,过M点作轴,∴,∴,,
∴,∴…………………………………………7分
(3)把代入得,,
把代入得,,
分三种情况:①当第三点在直线上时,,解得;
②当第三点在直线上时,,解得;
③当第三点在x轴上时,则,解得,
∴直线与直线,及x轴有3个不同的交点,且其中两点关于第三点对称,则a的值为或或13……………………………………………………………13分
同课章节目录
