广东省云浮市罗定市2023-2024学年高二下学期期中检测数学试题(图片版,无答案)
文档属性
| 名称 | 广东省云浮市罗定市2023-2024学年高二下学期期中检测数学试题(图片版,无答案) | 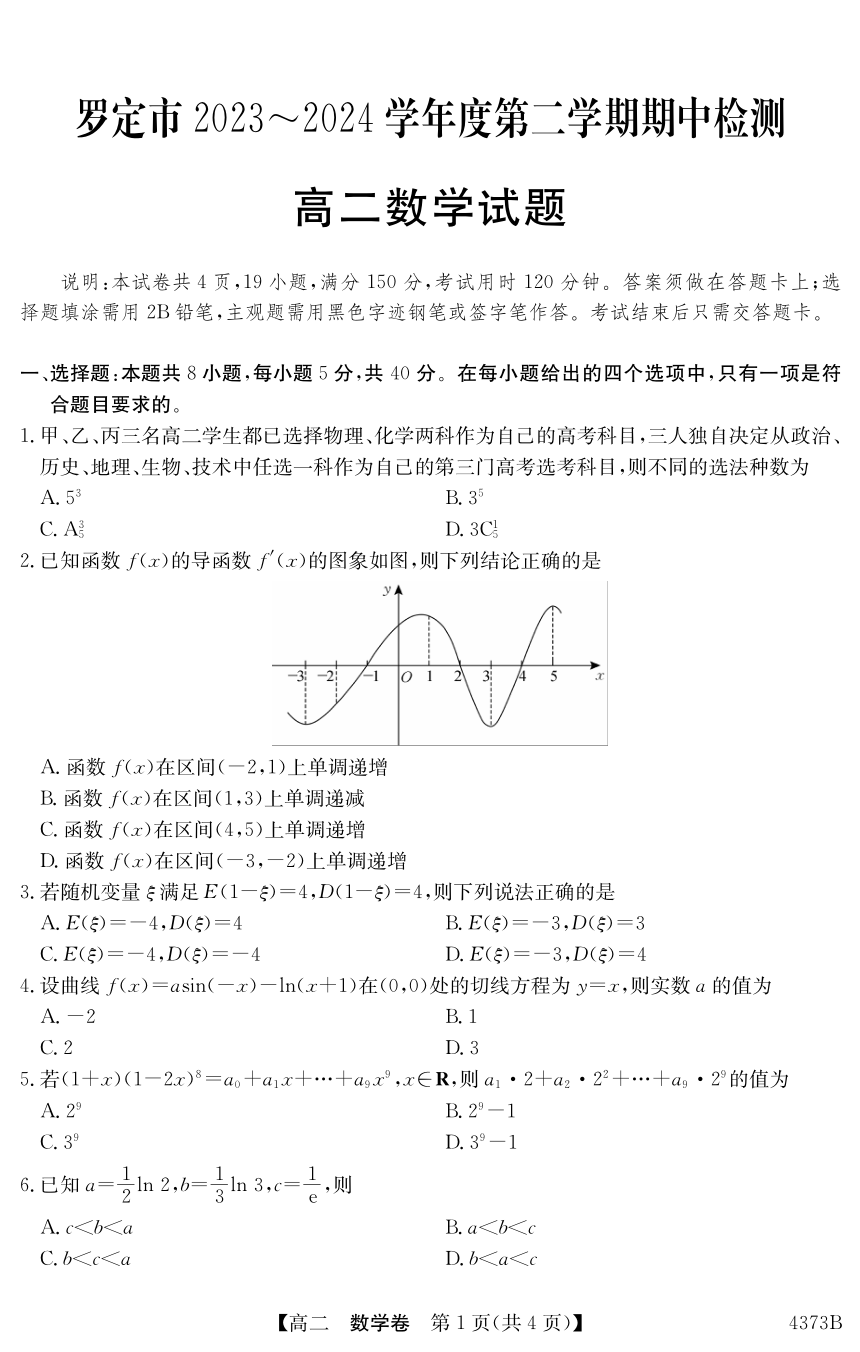 | |
| 格式 | |||
| 文件大小 | 388.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 10:54:25 | ||
图片预览


文档简介
罗定市2023~2024学年度第二学期期中检测
高二数学试题
说明:本试卷共4页,19小题,满分150分,考试用时120分钟。答案须做在答题卡上;选
择题填涂需用2B铅笔,主观题需用黑色字迹钢笔或签字笔作答。考试结束后只需交答题卡。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符
合题目要求的
1.甲、乙、丙三名高二学生都已选择物理、化学两科作为自己的高考科目,三人独自决定从政治、
历史、地理、生物、技术中任选一科作为自己的第三门高考选考科目,则不同的选法种数为
A.53
B.35
C.A
D.3CI
2.已知函数f(x)的导函数f(x)的图象如图,则下列结论正确的是
A.函数f(x)在区间(一2,1)上单调递增
B.函数f(x)在区间(1,3)上单调递减
C.函数f(x)在区间(4,5)上单调递增
D.函数f(x)在区间(一3,一2)上单调递增
3.若随机变量满足E(1一)=4,D(1一)=4,则下列说法正确的是
A.E()=-4,D()=4
B.E()=一3,D()=3
C.E()=-4,D()=-4
D.E()=-3,D()=4
4.设曲线f(x)=asin(一x)一ln(x十1)在(0,0)处的切线方程为y=x,则实数a的值为
A.-2
B.1
C.2
D.3
5.若(1十x)(1-2.x)8=ao十a1x十…十agx°,x∈R,则a1·2十a2·22十…十ag·2的值为
A.2
B.29-1
C.39
D.39-1
6.已知a=21n2.6=}n3c=是,则
A.cB.aC.bD.b【高二数学卷
第1页(共4页)】
4373B
7.国际高峰论坛上,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提
问,要求这3个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不
同的提问方式的种数为
A.198
B.268
C.306
D.378
8.数学家高斯在各个领域中都取得了重大的成就.在研究一类二次型数论问题时,他在他的著
作《算术研究》中首次引人了二次剩余的概念.二次剩余理论在嗓音工程学、密码学以及大数
分解等各个领域都有广泛的应用.已知对于正整数a,n(n≥2),若存在一个整数x,使得n整
除x2一a,则称a是n的一个二次剩余,否则为二次非剩余.从1到20这20个整数中随机抽
取一个整数a,记事件A=“a与12互质”,B=“a是12的二次非剩余”,则P(B引A)=
B号
c
D清
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的四个选项中,有多项符合要
求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
10.设随机变量的分布列为P(=号)=ak(k=1,23,4,5),则
A.15a=1
B.P(0.5C.P(0.1<0.5)=0.2
D.P(E=1)=0.3
1,已知函数f(x)=士11,则下列结论正确的是
A.函数f(x)存在三个不同的零点
B.函数f(x)既存在极大值又存在极小值
C若x∈[,十o)时,f()=怎.则的最小值为2
D.当一ek<0时,方程f(x)=k有且只有两个实根
三、填空题:本题共3小题,每小题5分,共15分。
12.设随机变量X服从两点分布,若P(X=1)一P(X=0)=0.2,则P(X=1)=
13.长期熬夜可能影响免疫力.据某医疗机构调查,某社区大约有20%的人免疫力低下,而该社
区大约有10%的人长期熬夜,长期熬夜的人中免疫力低下的概率约为40%,现从没有长期
熬夜的人中任意调查一人,则此人免疫力低下的概率为
14已知函数x)=十+202x+合,且满足f血)+f(-1)≤1,则实数x的值
为
【高二数学卷第2页(共4页)】
4373B
高二数学试题
说明:本试卷共4页,19小题,满分150分,考试用时120分钟。答案须做在答题卡上;选
择题填涂需用2B铅笔,主观题需用黑色字迹钢笔或签字笔作答。考试结束后只需交答题卡。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符
合题目要求的
1.甲、乙、丙三名高二学生都已选择物理、化学两科作为自己的高考科目,三人独自决定从政治、
历史、地理、生物、技术中任选一科作为自己的第三门高考选考科目,则不同的选法种数为
A.53
B.35
C.A
D.3CI
2.已知函数f(x)的导函数f(x)的图象如图,则下列结论正确的是
A.函数f(x)在区间(一2,1)上单调递增
B.函数f(x)在区间(1,3)上单调递减
C.函数f(x)在区间(4,5)上单调递增
D.函数f(x)在区间(一3,一2)上单调递增
3.若随机变量满足E(1一)=4,D(1一)=4,则下列说法正确的是
A.E()=-4,D()=4
B.E()=一3,D()=3
C.E()=-4,D()=-4
D.E()=-3,D()=4
4.设曲线f(x)=asin(一x)一ln(x十1)在(0,0)处的切线方程为y=x,则实数a的值为
A.-2
B.1
C.2
D.3
5.若(1十x)(1-2.x)8=ao十a1x十…十agx°,x∈R,则a1·2十a2·22十…十ag·2的值为
A.2
B.29-1
C.39
D.39-1
6.已知a=21n2.6=}n3c=是,则
A.c
第1页(共4页)】
4373B
7.国际高峰论坛上,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提
问,要求这3个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不
同的提问方式的种数为
A.198
B.268
C.306
D.378
8.数学家高斯在各个领域中都取得了重大的成就.在研究一类二次型数论问题时,他在他的著
作《算术研究》中首次引人了二次剩余的概念.二次剩余理论在嗓音工程学、密码学以及大数
分解等各个领域都有广泛的应用.已知对于正整数a,n(n≥2),若存在一个整数x,使得n整
除x2一a,则称a是n的一个二次剩余,否则为二次非剩余.从1到20这20个整数中随机抽
取一个整数a,记事件A=“a与12互质”,B=“a是12的二次非剩余”,则P(B引A)=
B号
c
D清
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的四个选项中,有多项符合要
求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.现有不同的红球4个,黄球5个,绿球6个,则下列说法正确的是
A.从中任选1个球,有15种不同的选法
B.若每种颜色选出1个球,有120种不同的选法
C.若要选出不同颜色的2个球,有31种不同的选法
D.若要不放回地依次选出2个球,有210种不同的选法
10.设随机变量的分布列为P(=号)=ak(k=1,23,4,5),则
A.15a=1
B.P(0.5
D.P(E=1)=0.3
1,已知函数f(x)=士11,则下列结论正确的是
A.函数f(x)存在三个不同的零点
B.函数f(x)既存在极大值又存在极小值
C若x∈[,十o)时,f()=怎.则的最小值为2
D.当一ek<0时,方程f(x)=k有且只有两个实根
三、填空题:本题共3小题,每小题5分,共15分。
12.设随机变量X服从两点分布,若P(X=1)一P(X=0)=0.2,则P(X=1)=
13.长期熬夜可能影响免疫力.据某医疗机构调查,某社区大约有20%的人免疫力低下,而该社
区大约有10%的人长期熬夜,长期熬夜的人中免疫力低下的概率约为40%,现从没有长期
熬夜的人中任意调查一人,则此人免疫力低下的概率为
14已知函数x)=十+202x+合,且满足f血)+f(-1)≤1,则实数x的值
为
【高二数学卷第2页(共4页)】
4373B
同课章节目录
