湖南省郴州市嘉禾县坦坪镇田心中学2023-2024学年七年级下学期期中数学试题(含答案)
文档属性
| 名称 | 湖南省郴州市嘉禾县坦坪镇田心中学2023-2024学年七年级下学期期中数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 955.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览


文档简介
七年级数学
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.
1.下列四个实数中,最小的是( )
A. B. C.2 D.3
2.为了解某中学1500名学生的视力情况,随机抽查了500名学生的视力进行统计分析,下列说法正确的是( )
A.500名学生的视力是总体的一个样本
B.500名学生是总体
C.500名学生是总体的一个个体
D.样本容量是1500名
3.下列运算正确的是( )
A. B. C. D.
4.如果点在x轴上,则点A的坐标为( )
A. B. C. D.
5.下列用消元法解二元一次方程组不正确的是( )
A.由①,得
B.由,得
C.由,得
D.把整体代入②,得
6.如图,,,若,则的度数为( )
A. B. C. D.
7.若一个不等式的正整数解为1,2,则该不等式的解集在数轴上的表示可能是下列的( )
A B C D
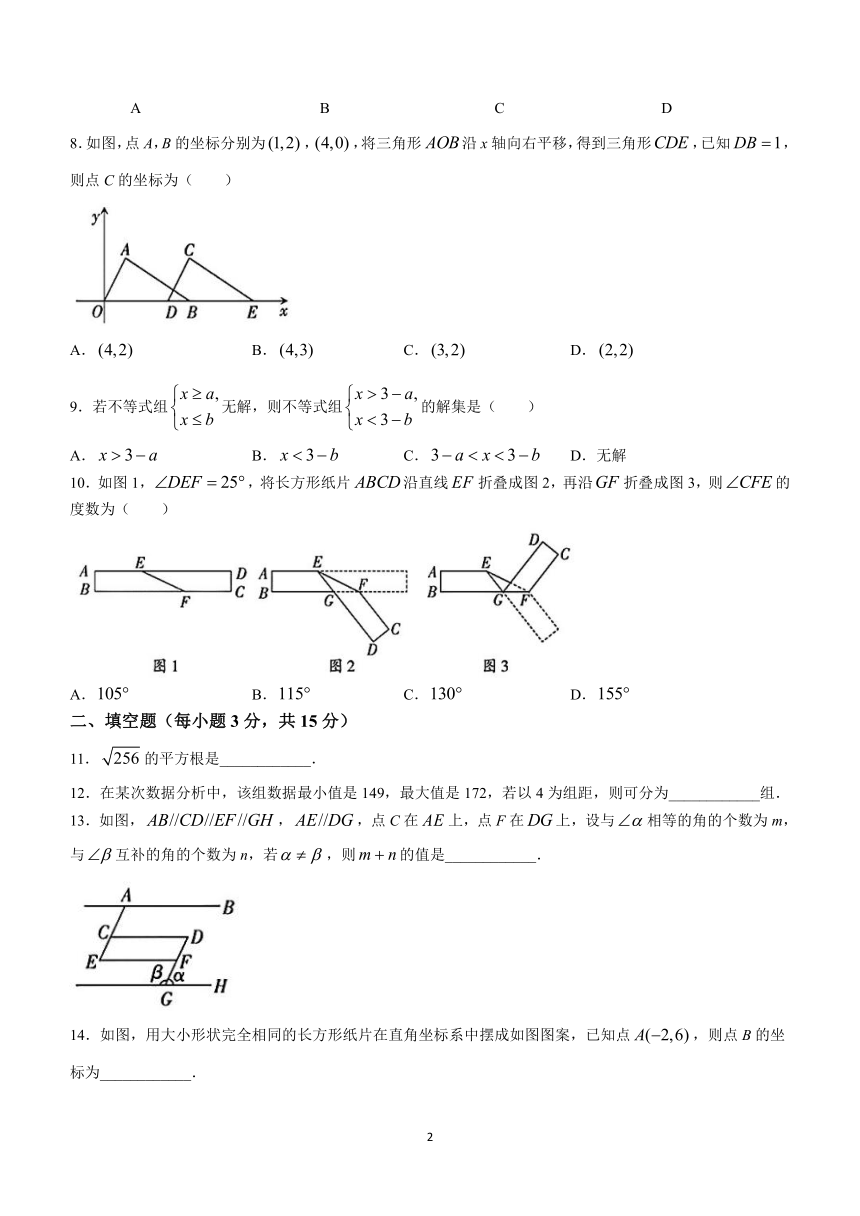
8.如图,点A,B的坐标分别为,,将三角形沿x轴向右平移,得到三角形,已知,则点C的坐标为( )
A. B. C. D.
9.若不等式组无解,则不等式组的解集是( )
A. B. C. D.无解
10.如图1,,将长方形纸片沿直线折叠成图2,再沿折叠成图3,则的度数为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.的平方根是____________.
12.在某次数据分析中,该组数据最小值是149,最大值是172,若以4为组距,则可分为____________组.
13.如图,,,点C在上,点F在上,设与相等的角的个数为m,与互补的角的个数为n,若,则的值是____________.
14.如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案,已知点,则点B的坐标为____________.
15.对于任意实数a,b,定义一种运算.请根据上述定义解决问题:若,且解集中有三个整数解,则m的取值范围是____________.
三、解答题(本大题共8个小题,共75分)
16.(8分)(1)计算:.
(2)若a是的整数部分,b是的立方根,求的值.
17.(8分)若点P的坐标为,其中x满足不等式组求点P所在的象限.
18.(8分)甲、乙两同学同时解关于x,y的方程组甲看错了m,解出的结果是乙看错了n,解出的结果是你能确定m,n的值和原方程组的解吗?
19.(8分)某校七年级共有400名学生,学校团委准备调查他们对垃圾分类的了解程度.
(1)下面有三种选取调查对象的方式:
①调查七年级部分女生;②调查七年级某个班的学生;③随机调查七年级每个班一定数量的学生.
你认为最合理的一种方式是____________(直接填写序号).
(2)学校团委采用了最合理的调查方式,并用收集到的数据绘制出两幅统计图(如图1、图2所示),请你根据图中信息,将两个统计图补充完整.
(3)根据此次调查结果,估计该校七年级有____________名学生对垃圾分类比较了解.
(4)根据此次调查结果,请你为学校团委开展垃圾分类主题教育活动提出合理化建议.
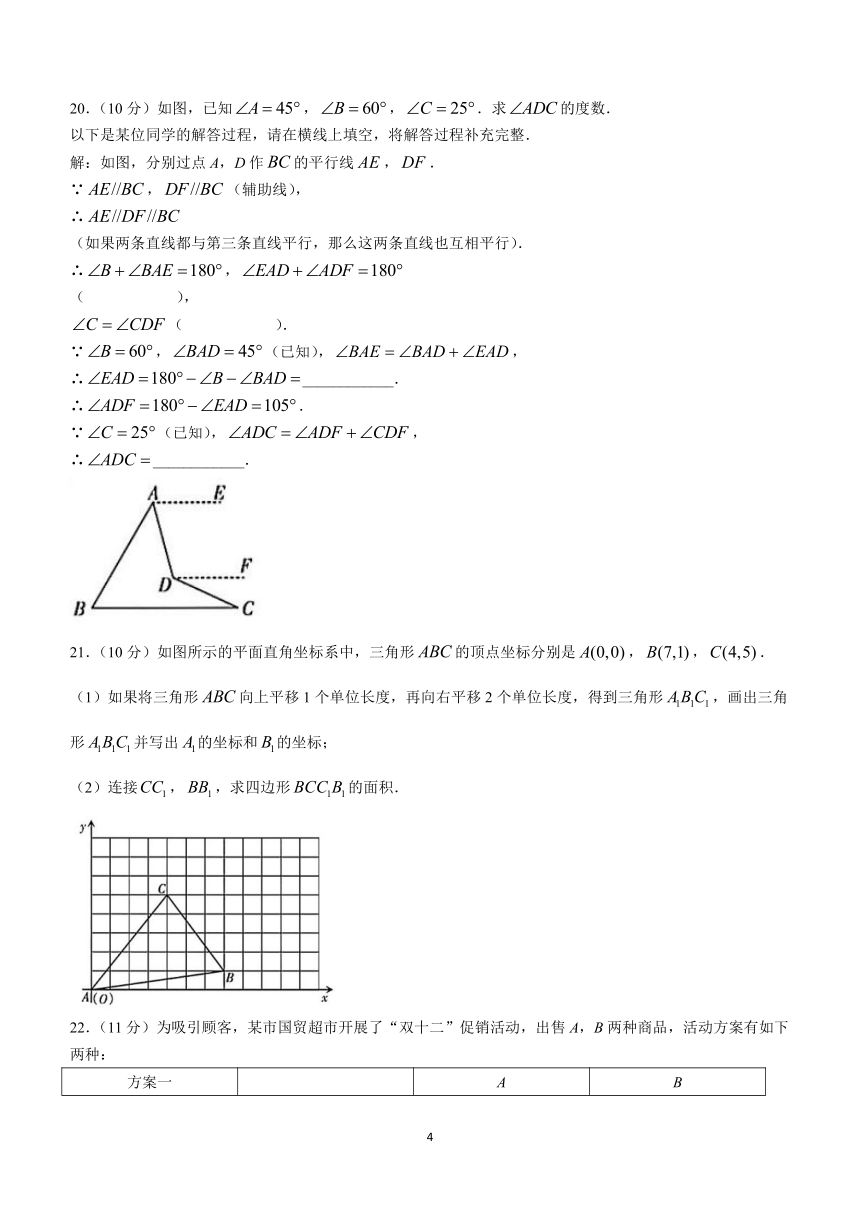
20.(10分)如图,已知,,.求的度数.
以下是某位同学的解答过程,请在横线上填空,将解答过程补充完整.
解:如图,分别过点A,D作的平行线,.
∵,(辅助线),
∴
(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴,
( ),
( ).
∵,(已知),,
∴____________.
∴.
∵(已知),,
∴____________.
21.(10分)如图所示的平面直角坐标系中,三角形的顶点坐标分别是,,.
(1)如果将三角形向上平移1个单位长度,再向右平移2个单位长度,得到三角形,画出三角形并写出的坐标和的坐标;
(2)连接,,求四边形的面积.
22.(11分)为吸引顾客,某市国贸超市开展了“双十二”促销活动,出售A,B两种商品,活动方案有如下两种:
方案一 A B
标价(单位:元/件) 50 80
每件商品返利 按标价的 按标价的
例:买一件A商品,只需付款元
方案二 若所购商品达到或超过51件(不同商品可累计),则按标价的返利.
(购买两种商品时只能参加同一种活动)
(1)某单位购买A商品40件,B商品95件,选用何种活动划算?能便宜多少钱?
(2)若某单位购买A商品x件(x为正整数),购买B商品的件数比A商品件数的2倍还多15件,请问该单位该如何选择才能获得最大优惠?请说明理由.
23.(12分)已知点A,C,B不在同一条直线上,.
(1)如图1,当,时,求的度数;
(2)如图2,,分别为,的平分线所在直线,试探究与的数量关系;
(3)如图3,在(2)的前提下,且有,,试求出的值.
七年级数学答案
一、选择题
1~5 BABDB 6~10 BCACA
9.【考点精讲】∵不等式组无解,∴.∴,.∴不等式组的解集为.故选C.
10.【考点精讲】题图1中,∵四边形是长方形,.∴,.∴.题图2中,根据折叠的性质,得.∴.题图3中,根据折叠的性质,得.∴.故选A.
二、填空题
11. 12.6
13.11【考点精讲】如图.
∵,,
∴,.
∵,∴与互补的角有,,,,,.
∴,.∴.
14.
15.【考点精讲】根据题意,得.
∵,∴,
即解不等式①,得.解不等式②,得.∵的解集中有三个整数解,∴三个整数解是1,0,.∴.解得.
三、解答题
16.解:(1)原式.
(2)根据题意,得.∵,即,∴.
∴.
17.解:解不等式①,得.解不等式②,得.∴不等式组的解集是.
∵,,∴点P的坐标为.
∴点P在第四象限.
18.解:能.把代入,得.解得.把代入,得.解得.∴原方程组为
,得.把代入①,得.解得.
∴原方程组的解为
19.解:(1)③
(2)按“了解一点”的人数为36补全条形统计图,按“了解一点”为、“比较了解”为补全扇形统计图.
(3)120
(4)加强垃圾分类的宣传力度.(答案合理即可)
20.解:两直线平行,同旁内角互补 两直线平行,内错角相等
21.解:(1)三角形如图所示.,.
(2)四边形的面积是.
22.解:(1)当该单位购买A商品40件,B商品95件时,
方案一需付款(元);
方案二需付款(元).
∵,∴选用方案二更划算,能便宜(元).
(2)当时.解得.分两种情况:
①当时.选择方案一能获得最大优惠;
②当时.方案一需付款;
方案二需付款.
当时.解得.此时方案一和方案二获得优惠一样.
当4时.解得.∴当时,选择方案一能获得最大优惠;
当时.解得.∴当时,选择方案二能获得最大优惠.
综上所述,当时,选择方案一能获得最大优惠;当时,选择方案一和方案二获得优惠一样;当时,选择方案二能获得最大优惠.
23.解:(1)过点C作,点F在点C左侧.
∵,∴.∴,.
∵,,
∴.
(2)过点Q作,点M在点Q右侧,延长交直线于点N.
∵,∴.∴,.
∵平分,平分,∴,.
∴.
由(1)得.
∴.∴.
(3)∵,平分,平分,
∴,.
∵,∴.
∵,∴.
∵,∴.
∴.∴,.
∴.
时间:100分钟 满分:120分
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.
1.下列四个实数中,最小的是( )
A. B. C.2 D.3
2.为了解某中学1500名学生的视力情况,随机抽查了500名学生的视力进行统计分析,下列说法正确的是( )
A.500名学生的视力是总体的一个样本
B.500名学生是总体
C.500名学生是总体的一个个体
D.样本容量是1500名
3.下列运算正确的是( )
A. B. C. D.
4.如果点在x轴上,则点A的坐标为( )
A. B. C. D.
5.下列用消元法解二元一次方程组不正确的是( )
A.由①,得
B.由,得
C.由,得
D.把整体代入②,得
6.如图,,,若,则的度数为( )
A. B. C. D.
7.若一个不等式的正整数解为1,2,则该不等式的解集在数轴上的表示可能是下列的( )
A B C D
8.如图,点A,B的坐标分别为,,将三角形沿x轴向右平移,得到三角形,已知,则点C的坐标为( )
A. B. C. D.
9.若不等式组无解,则不等式组的解集是( )
A. B. C. D.无解
10.如图1,,将长方形纸片沿直线折叠成图2,再沿折叠成图3,则的度数为( )
A. B. C. D.
二、填空题(每小题3分,共15分)
11.的平方根是____________.
12.在某次数据分析中,该组数据最小值是149,最大值是172,若以4为组距,则可分为____________组.
13.如图,,,点C在上,点F在上,设与相等的角的个数为m,与互补的角的个数为n,若,则的值是____________.
14.如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案,已知点,则点B的坐标为____________.
15.对于任意实数a,b,定义一种运算.请根据上述定义解决问题:若,且解集中有三个整数解,则m的取值范围是____________.
三、解答题(本大题共8个小题,共75分)
16.(8分)(1)计算:.
(2)若a是的整数部分,b是的立方根,求的值.
17.(8分)若点P的坐标为,其中x满足不等式组求点P所在的象限.
18.(8分)甲、乙两同学同时解关于x,y的方程组甲看错了m,解出的结果是乙看错了n,解出的结果是你能确定m,n的值和原方程组的解吗?
19.(8分)某校七年级共有400名学生,学校团委准备调查他们对垃圾分类的了解程度.
(1)下面有三种选取调查对象的方式:
①调查七年级部分女生;②调查七年级某个班的学生;③随机调查七年级每个班一定数量的学生.
你认为最合理的一种方式是____________(直接填写序号).
(2)学校团委采用了最合理的调查方式,并用收集到的数据绘制出两幅统计图(如图1、图2所示),请你根据图中信息,将两个统计图补充完整.
(3)根据此次调查结果,估计该校七年级有____________名学生对垃圾分类比较了解.
(4)根据此次调查结果,请你为学校团委开展垃圾分类主题教育活动提出合理化建议.
20.(10分)如图,已知,,.求的度数.
以下是某位同学的解答过程,请在横线上填空,将解答过程补充完整.
解:如图,分别过点A,D作的平行线,.
∵,(辅助线),
∴
(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
∴,
( ),
( ).
∵,(已知),,
∴____________.
∴.
∵(已知),,
∴____________.
21.(10分)如图所示的平面直角坐标系中,三角形的顶点坐标分别是,,.
(1)如果将三角形向上平移1个单位长度,再向右平移2个单位长度,得到三角形,画出三角形并写出的坐标和的坐标;
(2)连接,,求四边形的面积.
22.(11分)为吸引顾客,某市国贸超市开展了“双十二”促销活动,出售A,B两种商品,活动方案有如下两种:
方案一 A B
标价(单位:元/件) 50 80
每件商品返利 按标价的 按标价的
例:买一件A商品,只需付款元
方案二 若所购商品达到或超过51件(不同商品可累计),则按标价的返利.
(购买两种商品时只能参加同一种活动)
(1)某单位购买A商品40件,B商品95件,选用何种活动划算?能便宜多少钱?
(2)若某单位购买A商品x件(x为正整数),购买B商品的件数比A商品件数的2倍还多15件,请问该单位该如何选择才能获得最大优惠?请说明理由.
23.(12分)已知点A,C,B不在同一条直线上,.
(1)如图1,当,时,求的度数;
(2)如图2,,分别为,的平分线所在直线,试探究与的数量关系;
(3)如图3,在(2)的前提下,且有,,试求出的值.
七年级数学答案
一、选择题
1~5 BABDB 6~10 BCACA
9.【考点精讲】∵不等式组无解,∴.∴,.∴不等式组的解集为.故选C.
10.【考点精讲】题图1中,∵四边形是长方形,.∴,.∴.题图2中,根据折叠的性质,得.∴.题图3中,根据折叠的性质,得.∴.故选A.
二、填空题
11. 12.6
13.11【考点精讲】如图.
∵,,
∴,.
∵,∴与互补的角有,,,,,.
∴,.∴.
14.
15.【考点精讲】根据题意,得.
∵,∴,
即解不等式①,得.解不等式②,得.∵的解集中有三个整数解,∴三个整数解是1,0,.∴.解得.
三、解答题
16.解:(1)原式.
(2)根据题意,得.∵,即,∴.
∴.
17.解:解不等式①,得.解不等式②,得.∴不等式组的解集是.
∵,,∴点P的坐标为.
∴点P在第四象限.
18.解:能.把代入,得.解得.把代入,得.解得.∴原方程组为
,得.把代入①,得.解得.
∴原方程组的解为
19.解:(1)③
(2)按“了解一点”的人数为36补全条形统计图,按“了解一点”为、“比较了解”为补全扇形统计图.
(3)120
(4)加强垃圾分类的宣传力度.(答案合理即可)
20.解:两直线平行,同旁内角互补 两直线平行,内错角相等
21.解:(1)三角形如图所示.,.
(2)四边形的面积是.
22.解:(1)当该单位购买A商品40件,B商品95件时,
方案一需付款(元);
方案二需付款(元).
∵,∴选用方案二更划算,能便宜(元).
(2)当时.解得.分两种情况:
①当时.选择方案一能获得最大优惠;
②当时.方案一需付款;
方案二需付款.
当时.解得.此时方案一和方案二获得优惠一样.
当4时.解得.∴当时,选择方案一能获得最大优惠;
当时.解得.∴当时,选择方案二能获得最大优惠.
综上所述,当时,选择方案一能获得最大优惠;当时,选择方案一和方案二获得优惠一样;当时,选择方案二能获得最大优惠.
23.解:(1)过点C作,点F在点C左侧.
∵,∴.∴,.
∵,,
∴.
(2)过点Q作,点M在点Q右侧,延长交直线于点N.
∵,∴.∴,.
∵平分,平分,∴,.
∴.
由(1)得.
∴.∴.
(3)∵,平分,平分,
∴,.
∵,∴.
∵,∴.
∵,∴.
∴.∴,.
∴.
同课章节目录
