第1-4单元常考易错检测卷-数学五年级下册苏教版(含答案)
文档属性
| 名称 | 第1-4单元常考易错检测卷-数学五年级下册苏教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 553.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-03 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-4单元常考易错检测卷-数学五年级下册苏教版
一、选择题
1.把一张长18厘米、宽12厘米的长方形纸,剪成同样大小相等的正方形且没有剩余。这些正方形纸的边长最大是( )厘米。
A.6 B.3 C.2 D.4
2.小明一个星期中休息2天,休息日占工作日的( )。
A. B. C. D.
3.如果x=0.5×Y,那么x和Y的最大公因数是( )。
A.x B.Y C.x+Y D.xY
4.自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。下面表示每月的水费与用水量关系的是( )。
A. B.
C. D.
5.已知5a=8b,根据等式的性质,下列等式不成立的是( )。
A.75a=120b B.5a+12b=20b C.8a=11b D.2a=8b-3a
二、填空题
6.一个数既是2的倍数,又是5的倍数,这个数最小是( )。能同时被2、3、5整除的最小三位数是( )。
7.小明问爸爸的手机多少钱,爸爸说:是一个四位数,最高位既不是质数也不是合数;百位上既是奇数又是合数;最低位是最小的合数;剩下一个数既是偶数又是质数。这部手机是( )元。
8.(填小数)。
9.的分数单位是( ),它有( )个这样的分数单位,减去( )个这样的分数单位就是1。
10.3块饼平均分给4人,每人分得3块饼的,每人分得一块饼的。糖水中有7克糖和100克水,若加上2克糖,则糖占糖水的。
11.当时,( );当时,( )。
12.如图是某公司第一、第二门市部2019年营业额统计图。
(1)这是( )统计图,这一年中第( )季度两门市部营业额最接近,第( )季度两门市部营业额差距最大。
(2)第二门市部平均每季度营业额是( )万元。
(3)第四季度第二门市部营业额是第一门市部的( )(填分数)。
三、判断题
13.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
14.任意一个奇数加上1,和一定是2的倍数。( )
15.把42分解质因数。42=1×2×3×7。( )
16.分数可以分为真分数,假分数和带分数。( )
17.若x+2.6=7.6,则1.5x<7.5。( )
四、计算题
18.把下列各组分数通分,再比较大小。
和 和 和
19.解下列方程。
1.9x=7.6 6x-3.5x=1.8
1.8×4+2.5x=17.2 2x+4.8=5.6
20.看图列方程并解答。
五、解答题
21.刘老师买来两根长为48米和30米的彩带,剪成同样长的短彩带且没有剩余(取整米数),分给美术组的每位同学做手工。美术组至少有多少人?
22.学校体育室一共有204根跳绳,四年级5个班,每班借了24根。剩下的借给五年级4个班,平均每班借出多少根?
23.环保志愿队在社区回收废塑料袋和废电池,回收废塑料袋的质量是废电池质量的3倍,且废塑料袋比废电池多19.6千克。志愿队回收废塑料袋和废电池各多少千克?(用方程解)
24.一个书架有两层,上层书的本数比下层少75本,已知下层书的本数是上层的2.5倍,这个书架上层和下层各有多少本书?(列方程解答)
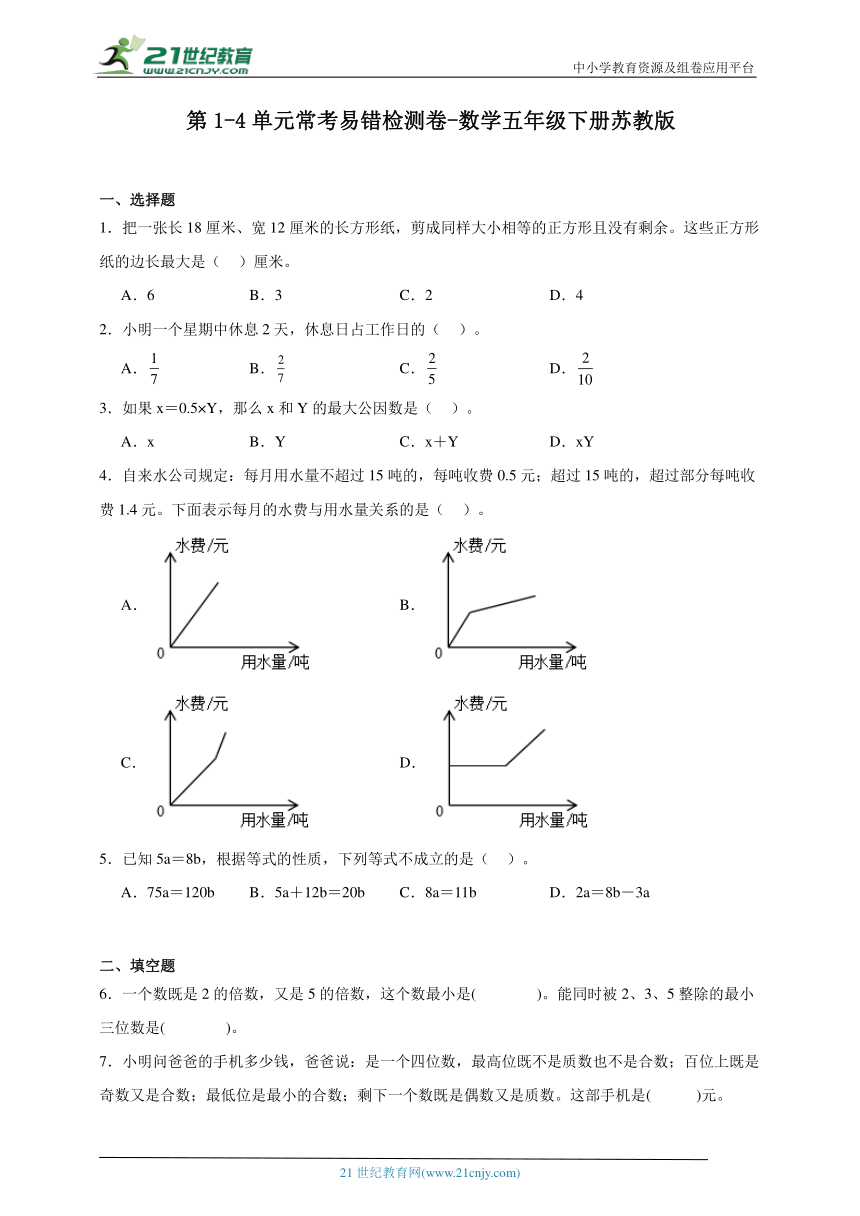
25.每年一度的徐州马拉松赛备受人们的关注,下面表示赛道的一部分,赛道在B处拐弯。根据赛会要求,需要在赛道的一侧摆放警示桩,相邻两个警示桩之间的距离必须相等,而且A、B、C处必须摆放一个,那么这段赛道最少要摆放多少个警示桩?
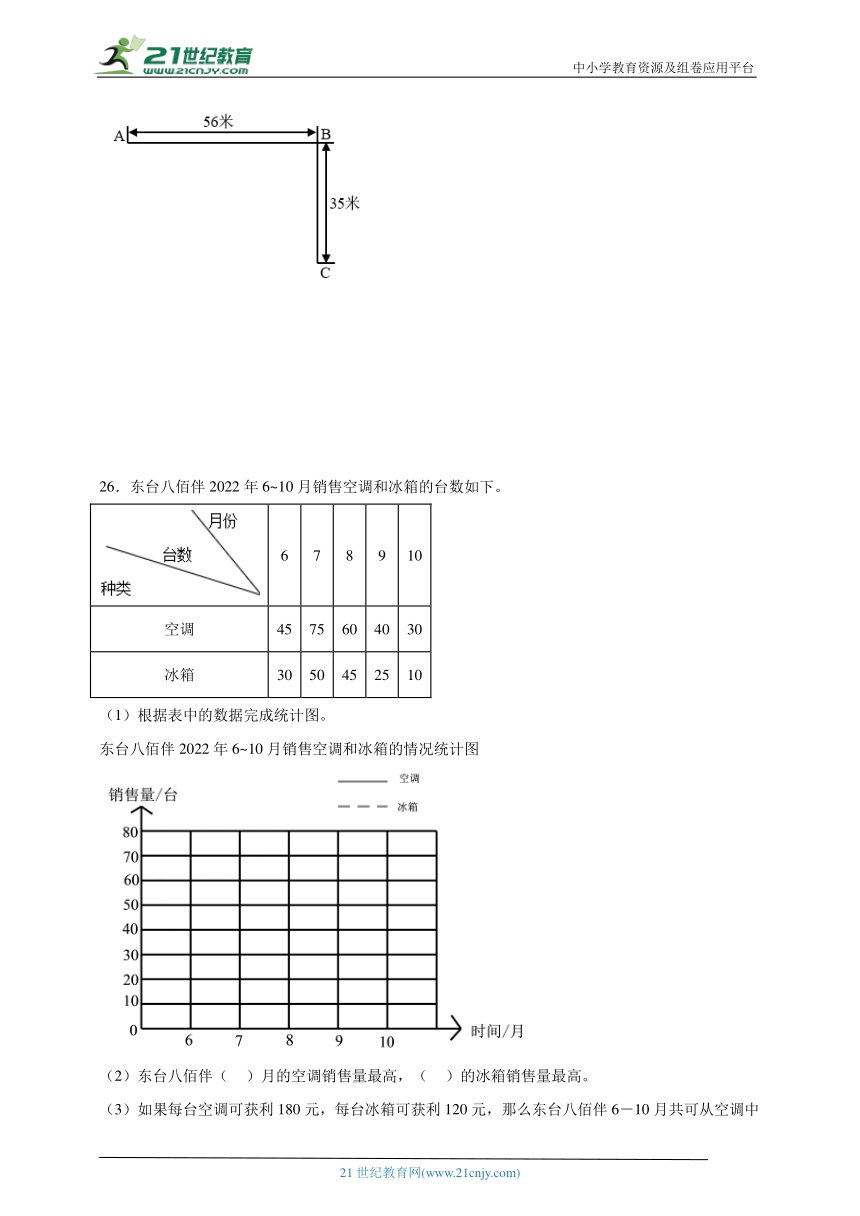
26.东台八佰伴2022年6~10月销售空调和冰箱的台数如下。
6 7 8 9 10
空调 45 75 60 40 30
冰箱 30 50 45 25 10
(1)根据表中的数据完成统计图。
东台八佰伴2022年6~10月销售空调和冰箱的情况统计图
(2)东台八佰伴( )月的空调销售量最高,( )的冰箱销售量最高。
(3)如果每台空调可获利180元,每台冰箱可获利120元,那么东台八佰伴6-10月共可从空调中获利( )元,从冰箱中平均每月可获利( )元。
(4)7月份后空调和冰箱的销售量总体上呈什么趋势?
参考答案:
1.A
【分析】要想使分成的小正方形个数最少,那么要使小正方形的边长最大,由此只要求得小正方形的边长最大是多少,也就是求得18和12的最大公因数是多少即可。
【详解】18=2×3×3
12=2×2×3
所以18和12的最大公因数是:2×3=6,即小正方形的边长至多是6厘米。
这些正方形的边长最大是6厘米。
故答案为:A
【点睛】本题关键是理解:要分成大小相等的小正方形,且没有剩余,就是小正方形的边长是18和12的公因数。
2.C
【分析】我国使用5天工作制,即一个星期中工作5天,休息2天。求一个星期中,休息日占工作日的几分之几,用休息天数除以工作日的天数(5天)。
【详解】2÷(7-2)
=2÷5
=
一个星期中,休息日占工作日的。
故答案为:C
【点睛】求一个数是另一个数的几分之几,把另一个数看作单位“1”,用这个数除以另一个数。
3.A
【分析】先把x=0.5×Y变形为Y÷x=2,根据为倍数关系的两个数的最大公因数是较小的数解答。
【详解】x=0.5×Y
Y÷x=1÷0.5
Y÷x=2
x和Y成倍数关系,x和Y的最大公因数是x。
如果x=0.5×Y,那么x和Y的最大公因数是x。
故答案为:A
【点睛】熟练掌握求两个数最大公因数的方法是解题的关键。
4.C
【分析】由于分段计费,所以图像是折线。每户每月用水量不超过15每吨价格为0.5元,超过15吨时超过部分每吨收费1.4元。所以15吨以内的总价和数量的折线上升较慢,超过15吨总价和数量的折线上升较快,据此选择即可。
【详解】A.,因为图像是一条直线,没有表示出超过15吨后水费与用水量的关系,不符合题意;
B.,没有准确表示超过15吨后水费和用水量的关系,不符合题意;
C.,能表示每月的水费与用水量关系,符合题意;
D.,图中没有表示出15吨以内水费与用水量的关系,不符合题意。
自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。表示每月的水费与用水量关系的是。
故答案为:C
【点睛】本题考查的目的是理解掌握折线统计图的特征及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.C
【分析】(1)等式的基本性质1:等式的两边同时加或减去一个相同的数,等式仍然成立。
(2)等式的基本性质2:等式的两边同时乘或除以一个相同的数(0除外),等式仍然成立。
【详解】5a=8b
5a×15=8b×15
75a=120b
等式成立;
B.5a+12b=8b+12b
5a+12b=20b
等式成立;
C.5a+3a=8b+3a
8a=8b+3a≠11b
等式不成立;
D.5a-3a=8b-3a
2a=8b-3a
等式成立。
故答案为:C
【点睛】此题主要考查学生对等式基本性质的理解与应用。
6. 10 120
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。5的倍数特征:个位上的数字是0或5的数是5的倍数。能同时被2和5整除的数个位上一定是0。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。能同时被2、5和3整除的数个位上一定是0,且各个数位上的数字和是3的倍数,据此解答。
【详解】一个数既是2的倍数,又是5的倍数,这个数最小是10。能同时被2、3、5整除的最小三位数是120。
7.1924
【分析】质数是指只能被1和它本身整除的数,合数是指除了1和它本身整除之外,还能被其它数整除的数;奇数是指不能被2整除的数,偶数是指能被2整除的数。这个四位数最高位是千位,既不是质数也不是合数的数是1,既是奇数又是合数的数是9,最低位是个位,最小的合数是4;十位上的数既是偶数又是质数,是2。据此可得出答案。
【详解】根据题意得:这个四位数的千位上是1,百位上是9,十位上是2,个位上是4,即这个四位数是1924。
8.16;9;20;0.75
【分析】从入手,根据分数与除法的关系,分数中的分子相当于除法中的被除数,分数中的分母相当于除法中的除数,根据分数的基本性质和商的变化规律进行转化;最后用除法算出结果(小数)即可。
【详解】
所以,。
9. 13 4
【分析】分母是几,它的分数单位就是几分之一;分子是几,就有几个这样的分数单位;把1化成分母是9的分数,再用13减去1化成分母是9的分数的分子,得到的差就是要减去几个这样的分数单位。
【详解】1=
13-9=4
的分数单位是,它有13个这样的分数单位,减去4个这样的分数单位就是1。
10.;;
【分析】把这些饼干的块数看作单位“1”,把它平均分成4份,每人分得1份,求每份是3块饼干的几分之几,用1除以4;用3块除以4是每人分得的块数,即块,是一块饼干的。
糖水中有7克糖和100克水,若加上2克糖,则糖的质量是(7+2)克,糖水的质量是(7+100+2)克,用糖的质量除以糖水的质量。
【详解】1÷4=
3÷4=(块)
块是一块饼干的
即3块饼平均分给4人,每人分得3块饼的,每人分得一块饼的。
(7+2)÷(7+100+2)
=9÷109
=
即糖水中有7克糖和100克水,若加上2克糖,则糖占糖水的。
【点睛】求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。求一个数是另一个数的几分之几,用这个数除以另一个数。
11. 36 6
【分析】先求出方程的解,再将x的值代入算式,即可求出的值是多少;然后求出方程的解,再将x的值代入算式,即可求出的值是多少。据此解答。
【详解】1+0.2x=3.6
1+0.2x-1=3.6-1
0.2x=2.6
0.2x÷0.2=2.6÷0.2
x=13
当x=13时,
5x-29
=5×13-29
=65-29
=36
73-3x=10
73-3x+3x=10+3x
73=10+3x
10+3x-10=73-10
3x-=63
3x÷3=63÷3
x=21
当x=21时,
1.8+x÷5
=1.8+21÷5
=1.8+4.2
=6
当时,36;当时,6。
【点睛】解答本题需熟练掌握根据等式的性质解方程及利用代入法求含有字母的式子的值的方法,准确计算。
12.(1) 复式折线/折线 三/3 四/4
(2)165
(3)
【分析】(1)折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;根据统计图的特征,可知这是复式折线统计图;先求出每个季度两门市部营业额的差,再比较即可。
(2)根据平均数的意义,先求出第二门市部一年的总营业额,再除以4即可求出每个季度的营业额。
(3)根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用第四季度第二门市部营业额除以第四季度第一门市部营业额,即可求出第四季度第二门市部营业额是第一门市部的几分之几。
【详解】(1)第一季度:200-175=25(万元)
第二季度:160-125=35(万元)
第三季度:150-140=10(万元)
第四季度:275-220=55(万元)
55>35>25>10
这是折线统计图,这一年中第三季度两门市部营业额最接近,第四季度两门市部营业额差距最大。
(2)(175+125+140+220)÷4
=660÷4
=165(万元)
第二门市部平均每季度的营业额是165万元。
(3)220÷275=
第四季度第二门市部营业额是第一门市部的。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
13.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
14.√
【分析】根据奇数、偶数的性质:奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数,据此解答。
【详解】在自然数中,是2的倍数的数叫做偶数,奇数+奇数=偶数,
因此,任意两个奇数的和都是2的倍数,1是奇数,所以任意一个奇数加上1,和一定是偶数,即是2的倍数,所以原题此说法正确。
故答案为:√
【点睛】此题考查的目的是理解偶数的意义,掌握奇数、偶数的性质。
15.×
【分析】分解质因数的意义,把一个合数写成几个质数相乘的形式叫做分解质因数,据此分析解答。
【详解】42=2×3×7,所以把42分解质因数,42=1×2×3×7是错误的;
故答案为:×
【点睛】本题主要考查分解质因数的意义,注意是几个质数相乘的形式,1既不是质数也不是合数。
16.×
【分析】分子小于分母的分数叫真分数,分子大于或等于分母的分数叫假分数;当假分数的分子是分母的倍数时,这个假分数可以改写成整数,当假分数的分子不是分母的倍数时,这个假分数可以改写成带分数。带分数只是假分数的一种形式。
【详解】分数可以分为真分数和假分数,带分数只是假分数的一种形式。所以原题错误。
故答案为:×
【点睛】此题重点考查假分数与带分数在意义上的关系。
17.×
【分析】先解方程x+2.6=7.6,然后计算出1.5x的值,看结果是否小于7.5即可。
【详解】x+2.6=7.6
x+2.6-2.6=7.6-2.6
x=5
当x=5时,1.5x=1.5×5=7.5
原题说法错误。
故答案为:×
【点睛】本题考查了方程的解法及利用代入法求值,需熟练掌握计算方法。
18.=;=;<;=;>;=;=;<
【分析】把异分母分数化成大小和原来相等的同分母分数叫做通分;再根据同分母分数比较大小的方法:分子大的分数就大,据此解答。
【详解】和
==
==
因为<,所以<。
和
==
因为>,所以>。
和
==
==
因为<,所以<。
19.x=4;
x=4;x=0.4
【分析】1.9x=7.6,方程两边同时除以1.9,方程得解;
6x-3.5x=1.8,合并未知数后得2.5x=1.8,方程两边同时除以2.5,方程得解;
1.8×4+2.5x=17.2,计算方程中的算术运算得7.2+2.5x=17.2,等式两边同时减7.2后再同时除以2.5,方程得解;
2x+4.8=5.6,等式两边同时减4.8后再同时除以2,方程得解;
【详解】1.9x=7.6
解:1.9x÷1.9=7.6÷1.9
x=4
6x-3.5x=1.8
解:2.5x=1.8
2.5x÷2.5=1.8÷2.5
1.8×4+2.5x=17.2
解:7.2+2.5x=17.2
7.2+2.5x-7.2=17.2-7.2
2.5x=10
2.5x÷2.5=10÷2.5
x=4
2x+4.8=5.6
解:2x+4.8-4.8=5.6-4.8
2x=0.8
2x÷2=0.8÷2
x=0.4
20.3x+38.6=53
x=4.8
【分析】看图,3个杯子的总价+一个茶壶的价钱38.6元=53元,据此列方程计算即可。
【详解】3x+38.6=53
解:3x+38.6-38.6=53-38.6
3x=14.4
3x÷3=14.4÷3
x=4.8
21.13人
【分析】先求出48和30的最大公因数,再将两根彩带的长度相加,求出总长度再除以最大公因数,即可解答。
【详解】48=2×2×2×2×3
30=2×3×5
48和30的最大公因数是2×3=6。
(48+30)÷6
=78÷6
=13(人)
答:美术组至少有13人。
【点睛】本题考查公因数的计算及应用。理解题意,找出最大公因数是解决本题的关键。
22.21根
【分析】设平均每班借出x根跳绳,五年级4个班,借出4x根跳绳,四年级有5个班,每班借了24根,5个班借了24×5根,四年级借跳绳的数量+五年级借跳绳的数量=204根跳绳,列方程:4x+24×5=204,解方程,即可解答。
【详解】解:设平均每班借出x根。
4x+24×5=204
4x+120=204
4x+120-120=204-120
4x=84
4x÷4=84÷4
x=21
答:平均每班借出21根。
【点睛】本题考查方程的实际应用,利用四年级借了跳绳的数量和五年级借了跳绳的数量以及五年级每班借了跳绳的数量和跳绳总量之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.回收废塑料袋29.4千克,回收废电池9.8千克
【分析】设志愿队回收废电池x千克,则回收废塑料袋3x千克,根据等量关系:回收废塑料袋质量-回收废电池的质量=19.6千克,列方程解答即可。
【详解】解:设志愿队回收废电池x千克,则回收废塑料袋3x千克。
3x-x=19.6
2x=19.6
2x÷2=19.6÷2
x=9.8
9.8×3=29.4(千克)
答:志愿队回收废塑料袋29.4千克,废电池9.8千克。
【点睛】本题主要考查了列方程解应用题,关键是找等量关系。
24.上层书架有50本;下层书架有125本
【分析】根据题意可知,上层书的本数×2.5=下层书的本数,下层书的本数-上层书的本数=75本,据此设上层书架有x本,下层书架有2.5x本,列方程为2.5x-x=75,然后解出方程即可。
【详解】解:设上层书架有x本,下层书架有2.5x本。
2.5x-x=75
1.5x=75
1.5x÷1.5=75÷1.5
x=50
50×2.5=125(本)
答:上层书架有50本,下层书架有125本。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
25.至少安排14个警示桩
【分析】利用求几个数的最大公因数的方法是:这几个数的公有的质因数的乘积就是这几个数的最大公因数,这个最大公因数就是间距,进一步求出警示桩个数。
【详解】56=2×2×2×7
35=5×7
最大公约数是7。
(56+35)÷7
=91÷7
=13(个)
13+1=14(个)
答:这段赛道至少安排14个警示桩。
【点睛】此题主要考查了求最大公因数的方法。
26.(1)见详解;(2)7;7;(3)45000;3840;(4)7月份后空调和冰箱的销售量总体上呈下降趋势
【分析】(1)根据统计表的数据,描出各点,再依次连接;
(2)找到空调对应折线的最高点,最高点在哪个月,哪个月的空调销售量最高,找到冰箱对应折线的最高点,最高点在哪个月,哪个月的冰箱销售量最高;
(3)先用加法计算出6-10月卖出的空调总数,然后根据单价×数量=总价,用空调总数乘180元,即可求出一共可从空调中获利多少元;先根据平均数=总数量÷总月份,用加法计算出6-10月卖出的冰箱总数,然后用冰箱总数除以5,即可求出平均每月卖出的数量,再乘120,即可求出从冰箱中平均每月可获利多少元。
(4)观察折线的走势判断它们是上升还是下降趋势。
【详解】(1)如图:
(2)东台八佰伴7月的空调销售量最高,7的冰箱销售量最高。
(3)(45+75+60+40+30)×180
=250×180
=45000(元)
(30+50+45+25+10)÷5×120
=160÷5×120
=3840(元)
如果每台空调可获利180元,每台冰箱可获利120元,那么东台八佰伴6-10月共可从空调中获利45000元,从冰箱中平均每月可获利3840元。
(4)观察统计图可知,7月份后空调和冰箱的销售量总体上呈下降趋势。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-4单元常考易错检测卷-数学五年级下册苏教版
一、选择题
1.把一张长18厘米、宽12厘米的长方形纸,剪成同样大小相等的正方形且没有剩余。这些正方形纸的边长最大是( )厘米。
A.6 B.3 C.2 D.4
2.小明一个星期中休息2天,休息日占工作日的( )。
A. B. C. D.
3.如果x=0.5×Y,那么x和Y的最大公因数是( )。
A.x B.Y C.x+Y D.xY
4.自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。下面表示每月的水费与用水量关系的是( )。
A. B.
C. D.
5.已知5a=8b,根据等式的性质,下列等式不成立的是( )。
A.75a=120b B.5a+12b=20b C.8a=11b D.2a=8b-3a
二、填空题
6.一个数既是2的倍数,又是5的倍数,这个数最小是( )。能同时被2、3、5整除的最小三位数是( )。
7.小明问爸爸的手机多少钱,爸爸说:是一个四位数,最高位既不是质数也不是合数;百位上既是奇数又是合数;最低位是最小的合数;剩下一个数既是偶数又是质数。这部手机是( )元。
8.(填小数)。
9.的分数单位是( ),它有( )个这样的分数单位,减去( )个这样的分数单位就是1。
10.3块饼平均分给4人,每人分得3块饼的,每人分得一块饼的。糖水中有7克糖和100克水,若加上2克糖,则糖占糖水的。
11.当时,( );当时,( )。
12.如图是某公司第一、第二门市部2019年营业额统计图。
(1)这是( )统计图,这一年中第( )季度两门市部营业额最接近,第( )季度两门市部营业额差距最大。
(2)第二门市部平均每季度营业额是( )万元。
(3)第四季度第二门市部营业额是第一门市部的( )(填分数)。
三、判断题
13.某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。( )
14.任意一个奇数加上1,和一定是2的倍数。( )
15.把42分解质因数。42=1×2×3×7。( )
16.分数可以分为真分数,假分数和带分数。( )
17.若x+2.6=7.6,则1.5x<7.5。( )
四、计算题
18.把下列各组分数通分,再比较大小。
和 和 和
19.解下列方程。
1.9x=7.6 6x-3.5x=1.8
1.8×4+2.5x=17.2 2x+4.8=5.6
20.看图列方程并解答。
五、解答题
21.刘老师买来两根长为48米和30米的彩带,剪成同样长的短彩带且没有剩余(取整米数),分给美术组的每位同学做手工。美术组至少有多少人?
22.学校体育室一共有204根跳绳,四年级5个班,每班借了24根。剩下的借给五年级4个班,平均每班借出多少根?
23.环保志愿队在社区回收废塑料袋和废电池,回收废塑料袋的质量是废电池质量的3倍,且废塑料袋比废电池多19.6千克。志愿队回收废塑料袋和废电池各多少千克?(用方程解)
24.一个书架有两层,上层书的本数比下层少75本,已知下层书的本数是上层的2.5倍,这个书架上层和下层各有多少本书?(列方程解答)
25.每年一度的徐州马拉松赛备受人们的关注,下面表示赛道的一部分,赛道在B处拐弯。根据赛会要求,需要在赛道的一侧摆放警示桩,相邻两个警示桩之间的距离必须相等,而且A、B、C处必须摆放一个,那么这段赛道最少要摆放多少个警示桩?
26.东台八佰伴2022年6~10月销售空调和冰箱的台数如下。
6 7 8 9 10
空调 45 75 60 40 30
冰箱 30 50 45 25 10
(1)根据表中的数据完成统计图。
东台八佰伴2022年6~10月销售空调和冰箱的情况统计图
(2)东台八佰伴( )月的空调销售量最高,( )的冰箱销售量最高。
(3)如果每台空调可获利180元,每台冰箱可获利120元,那么东台八佰伴6-10月共可从空调中获利( )元,从冰箱中平均每月可获利( )元。
(4)7月份后空调和冰箱的销售量总体上呈什么趋势?
参考答案:
1.A
【分析】要想使分成的小正方形个数最少,那么要使小正方形的边长最大,由此只要求得小正方形的边长最大是多少,也就是求得18和12的最大公因数是多少即可。
【详解】18=2×3×3
12=2×2×3
所以18和12的最大公因数是:2×3=6,即小正方形的边长至多是6厘米。
这些正方形的边长最大是6厘米。
故答案为:A
【点睛】本题关键是理解:要分成大小相等的小正方形,且没有剩余,就是小正方形的边长是18和12的公因数。
2.C
【分析】我国使用5天工作制,即一个星期中工作5天,休息2天。求一个星期中,休息日占工作日的几分之几,用休息天数除以工作日的天数(5天)。
【详解】2÷(7-2)
=2÷5
=
一个星期中,休息日占工作日的。
故答案为:C
【点睛】求一个数是另一个数的几分之几,把另一个数看作单位“1”,用这个数除以另一个数。
3.A
【分析】先把x=0.5×Y变形为Y÷x=2,根据为倍数关系的两个数的最大公因数是较小的数解答。
【详解】x=0.5×Y
Y÷x=1÷0.5
Y÷x=2
x和Y成倍数关系,x和Y的最大公因数是x。
如果x=0.5×Y,那么x和Y的最大公因数是x。
故答案为:A
【点睛】熟练掌握求两个数最大公因数的方法是解题的关键。
4.C
【分析】由于分段计费,所以图像是折线。每户每月用水量不超过15每吨价格为0.5元,超过15吨时超过部分每吨收费1.4元。所以15吨以内的总价和数量的折线上升较慢,超过15吨总价和数量的折线上升较快,据此选择即可。
【详解】A.,因为图像是一条直线,没有表示出超过15吨后水费与用水量的关系,不符合题意;
B.,没有准确表示超过15吨后水费和用水量的关系,不符合题意;
C.,能表示每月的水费与用水量关系,符合题意;
D.,图中没有表示出15吨以内水费与用水量的关系,不符合题意。
自来水公司规定:每月用水量不超过15吨的,每吨收费0.5元;超过15吨的,超过部分每吨收费1.4元。表示每月的水费与用水量关系的是。
故答案为:C
【点睛】本题考查的目的是理解掌握折线统计图的特征及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
5.C
【分析】(1)等式的基本性质1:等式的两边同时加或减去一个相同的数,等式仍然成立。
(2)等式的基本性质2:等式的两边同时乘或除以一个相同的数(0除外),等式仍然成立。
【详解】5a=8b
5a×15=8b×15
75a=120b
等式成立;
B.5a+12b=8b+12b
5a+12b=20b
等式成立;
C.5a+3a=8b+3a
8a=8b+3a≠11b
等式不成立;
D.5a-3a=8b-3a
2a=8b-3a
等式成立。
故答案为:C
【点睛】此题主要考查学生对等式基本性质的理解与应用。
6. 10 120
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。5的倍数特征:个位上的数字是0或5的数是5的倍数。能同时被2和5整除的数个位上一定是0。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。能同时被2、5和3整除的数个位上一定是0,且各个数位上的数字和是3的倍数,据此解答。
【详解】一个数既是2的倍数,又是5的倍数,这个数最小是10。能同时被2、3、5整除的最小三位数是120。
7.1924
【分析】质数是指只能被1和它本身整除的数,合数是指除了1和它本身整除之外,还能被其它数整除的数;奇数是指不能被2整除的数,偶数是指能被2整除的数。这个四位数最高位是千位,既不是质数也不是合数的数是1,既是奇数又是合数的数是9,最低位是个位,最小的合数是4;十位上的数既是偶数又是质数,是2。据此可得出答案。
【详解】根据题意得:这个四位数的千位上是1,百位上是9,十位上是2,个位上是4,即这个四位数是1924。
8.16;9;20;0.75
【分析】从入手,根据分数与除法的关系,分数中的分子相当于除法中的被除数,分数中的分母相当于除法中的除数,根据分数的基本性质和商的变化规律进行转化;最后用除法算出结果(小数)即可。
【详解】
所以,。
9. 13 4
【分析】分母是几,它的分数单位就是几分之一;分子是几,就有几个这样的分数单位;把1化成分母是9的分数,再用13减去1化成分母是9的分数的分子,得到的差就是要减去几个这样的分数单位。
【详解】1=
13-9=4
的分数单位是,它有13个这样的分数单位,减去4个这样的分数单位就是1。
10.;;
【分析】把这些饼干的块数看作单位“1”,把它平均分成4份,每人分得1份,求每份是3块饼干的几分之几,用1除以4;用3块除以4是每人分得的块数,即块,是一块饼干的。
糖水中有7克糖和100克水,若加上2克糖,则糖的质量是(7+2)克,糖水的质量是(7+100+2)克,用糖的质量除以糖水的质量。
【详解】1÷4=
3÷4=(块)
块是一块饼干的
即3块饼平均分给4人,每人分得3块饼的,每人分得一块饼的。
(7+2)÷(7+100+2)
=9÷109
=
即糖水中有7克糖和100克水,若加上2克糖,则糖占糖水的。
【点睛】求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量。注意:分率不能带单位名称,而具体的数量要带单位名称。求一个数是另一个数的几分之几,用这个数除以另一个数。
11. 36 6
【分析】先求出方程的解,再将x的值代入算式,即可求出的值是多少;然后求出方程的解,再将x的值代入算式,即可求出的值是多少。据此解答。
【详解】1+0.2x=3.6
1+0.2x-1=3.6-1
0.2x=2.6
0.2x÷0.2=2.6÷0.2
x=13
当x=13时,
5x-29
=5×13-29
=65-29
=36
73-3x=10
73-3x+3x=10+3x
73=10+3x
10+3x-10=73-10
3x-=63
3x÷3=63÷3
x=21
当x=21时,
1.8+x÷5
=1.8+21÷5
=1.8+4.2
=6
当时,36;当时,6。
【点睛】解答本题需熟练掌握根据等式的性质解方程及利用代入法求含有字母的式子的值的方法,准确计算。
12.(1) 复式折线/折线 三/3 四/4
(2)165
(3)
【分析】(1)折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;根据统计图的特征,可知这是复式折线统计图;先求出每个季度两门市部营业额的差,再比较即可。
(2)根据平均数的意义,先求出第二门市部一年的总营业额,再除以4即可求出每个季度的营业额。
(3)根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用第四季度第二门市部营业额除以第四季度第一门市部营业额,即可求出第四季度第二门市部营业额是第一门市部的几分之几。
【详解】(1)第一季度:200-175=25(万元)
第二季度:160-125=35(万元)
第三季度:150-140=10(万元)
第四季度:275-220=55(万元)
55>35>25>10
这是折线统计图,这一年中第三季度两门市部营业额最接近,第四季度两门市部营业额差距最大。
(2)(175+125+140+220)÷4
=660÷4
=165(万元)
第二门市部平均每季度的营业额是165万元。
(3)220÷275=
第四季度第二门市部营业额是第一门市部的。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
13.√
【分析】折线统计图:能够反应数量的多少,能够反映出数量的增减变化情况;条形统计图:能够清楚的反映出数量的多少,由此即可判断。
【详解】由分析可知:
某医院要反映每天的疫苗接种人数变化情况,应选用折线统计图。原题说法正确。
故答案为:√
【点睛】本题主要考查统计图的特点,熟练掌握折线统计图和条形统计图的特点并灵活运用。
14.√
【分析】根据奇数、偶数的性质:奇数+奇数=偶数,奇数+偶数=奇数,偶数+偶数=偶数,据此解答。
【详解】在自然数中,是2的倍数的数叫做偶数,奇数+奇数=偶数,
因此,任意两个奇数的和都是2的倍数,1是奇数,所以任意一个奇数加上1,和一定是偶数,即是2的倍数,所以原题此说法正确。
故答案为:√
【点睛】此题考查的目的是理解偶数的意义,掌握奇数、偶数的性质。
15.×
【分析】分解质因数的意义,把一个合数写成几个质数相乘的形式叫做分解质因数,据此分析解答。
【详解】42=2×3×7,所以把42分解质因数,42=1×2×3×7是错误的;
故答案为:×
【点睛】本题主要考查分解质因数的意义,注意是几个质数相乘的形式,1既不是质数也不是合数。
16.×
【分析】分子小于分母的分数叫真分数,分子大于或等于分母的分数叫假分数;当假分数的分子是分母的倍数时,这个假分数可以改写成整数,当假分数的分子不是分母的倍数时,这个假分数可以改写成带分数。带分数只是假分数的一种形式。
【详解】分数可以分为真分数和假分数,带分数只是假分数的一种形式。所以原题错误。
故答案为:×
【点睛】此题重点考查假分数与带分数在意义上的关系。
17.×
【分析】先解方程x+2.6=7.6,然后计算出1.5x的值,看结果是否小于7.5即可。
【详解】x+2.6=7.6
x+2.6-2.6=7.6-2.6
x=5
当x=5时,1.5x=1.5×5=7.5
原题说法错误。
故答案为:×
【点睛】本题考查了方程的解法及利用代入法求值,需熟练掌握计算方法。
18.=;=;<;=;>;=;=;<
【分析】把异分母分数化成大小和原来相等的同分母分数叫做通分;再根据同分母分数比较大小的方法:分子大的分数就大,据此解答。
【详解】和
==
==
因为<,所以<。
和
==
因为>,所以>。
和
==
==
因为<,所以<。
19.x=4;
x=4;x=0.4
【分析】1.9x=7.6,方程两边同时除以1.9,方程得解;
6x-3.5x=1.8,合并未知数后得2.5x=1.8,方程两边同时除以2.5,方程得解;
1.8×4+2.5x=17.2,计算方程中的算术运算得7.2+2.5x=17.2,等式两边同时减7.2后再同时除以2.5,方程得解;
2x+4.8=5.6,等式两边同时减4.8后再同时除以2,方程得解;
【详解】1.9x=7.6
解:1.9x÷1.9=7.6÷1.9
x=4
6x-3.5x=1.8
解:2.5x=1.8
2.5x÷2.5=1.8÷2.5
1.8×4+2.5x=17.2
解:7.2+2.5x=17.2
7.2+2.5x-7.2=17.2-7.2
2.5x=10
2.5x÷2.5=10÷2.5
x=4
2x+4.8=5.6
解:2x+4.8-4.8=5.6-4.8
2x=0.8
2x÷2=0.8÷2
x=0.4
20.3x+38.6=53
x=4.8
【分析】看图,3个杯子的总价+一个茶壶的价钱38.6元=53元,据此列方程计算即可。
【详解】3x+38.6=53
解:3x+38.6-38.6=53-38.6
3x=14.4
3x÷3=14.4÷3
x=4.8
21.13人
【分析】先求出48和30的最大公因数,再将两根彩带的长度相加,求出总长度再除以最大公因数,即可解答。
【详解】48=2×2×2×2×3
30=2×3×5
48和30的最大公因数是2×3=6。
(48+30)÷6
=78÷6
=13(人)
答:美术组至少有13人。
【点睛】本题考查公因数的计算及应用。理解题意,找出最大公因数是解决本题的关键。
22.21根
【分析】设平均每班借出x根跳绳,五年级4个班,借出4x根跳绳,四年级有5个班,每班借了24根,5个班借了24×5根,四年级借跳绳的数量+五年级借跳绳的数量=204根跳绳,列方程:4x+24×5=204,解方程,即可解答。
【详解】解:设平均每班借出x根。
4x+24×5=204
4x+120=204
4x+120-120=204-120
4x=84
4x÷4=84÷4
x=21
答:平均每班借出21根。
【点睛】本题考查方程的实际应用,利用四年级借了跳绳的数量和五年级借了跳绳的数量以及五年级每班借了跳绳的数量和跳绳总量之间的关系,设出未知数,找出相关的量,列方程,解方程。
23.回收废塑料袋29.4千克,回收废电池9.8千克
【分析】设志愿队回收废电池x千克,则回收废塑料袋3x千克,根据等量关系:回收废塑料袋质量-回收废电池的质量=19.6千克,列方程解答即可。
【详解】解:设志愿队回收废电池x千克,则回收废塑料袋3x千克。
3x-x=19.6
2x=19.6
2x÷2=19.6÷2
x=9.8
9.8×3=29.4(千克)
答:志愿队回收废塑料袋29.4千克,废电池9.8千克。
【点睛】本题主要考查了列方程解应用题,关键是找等量关系。
24.上层书架有50本;下层书架有125本
【分析】根据题意可知,上层书的本数×2.5=下层书的本数,下层书的本数-上层书的本数=75本,据此设上层书架有x本,下层书架有2.5x本,列方程为2.5x-x=75,然后解出方程即可。
【详解】解:设上层书架有x本,下层书架有2.5x本。
2.5x-x=75
1.5x=75
1.5x÷1.5=75÷1.5
x=50
50×2.5=125(本)
答:上层书架有50本,下层书架有125本。
【点睛】本题考查了列方程解决问题,找到相应的数量关系式是解答本题的关键。
25.至少安排14个警示桩
【分析】利用求几个数的最大公因数的方法是:这几个数的公有的质因数的乘积就是这几个数的最大公因数,这个最大公因数就是间距,进一步求出警示桩个数。
【详解】56=2×2×2×7
35=5×7
最大公约数是7。
(56+35)÷7
=91÷7
=13(个)
13+1=14(个)
答:这段赛道至少安排14个警示桩。
【点睛】此题主要考查了求最大公因数的方法。
26.(1)见详解;(2)7;7;(3)45000;3840;(4)7月份后空调和冰箱的销售量总体上呈下降趋势
【分析】(1)根据统计表的数据,描出各点,再依次连接;
(2)找到空调对应折线的最高点,最高点在哪个月,哪个月的空调销售量最高,找到冰箱对应折线的最高点,最高点在哪个月,哪个月的冰箱销售量最高;
(3)先用加法计算出6-10月卖出的空调总数,然后根据单价×数量=总价,用空调总数乘180元,即可求出一共可从空调中获利多少元;先根据平均数=总数量÷总月份,用加法计算出6-10月卖出的冰箱总数,然后用冰箱总数除以5,即可求出平均每月卖出的数量,再乘120,即可求出从冰箱中平均每月可获利多少元。
(4)观察折线的走势判断它们是上升还是下降趋势。
【详解】(1)如图:
(2)东台八佰伴7月的空调销售量最高,7的冰箱销售量最高。
(3)(45+75+60+40+30)×180
=250×180
=45000(元)
(30+50+45+25+10)÷5×120
=160÷5×120
=3840(元)
如果每台空调可获利180元,每台冰箱可获利120元,那么东台八佰伴6-10月共可从空调中获利45000元,从冰箱中平均每月可获利3840元。
(4)观察统计图可知,7月份后空调和冰箱的销售量总体上呈下降趋势。
【点睛】此题考查的目的是理解掌握统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
