浙江省苍南县龙港高级中学高二(上)数学期末模拟试卷1
文档属性
| 名称 | 浙江省苍南县龙港高级中学高二(上)数学期末模拟试卷1 |

|
|
| 格式 | rar | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-16 22:57:00 | ||
图片预览


文档简介
龙港高中高二数学(理科)期末模拟试题1
参考公式和数据:
用最小二乘法求线性回归直线方程系数公式,.
正态分布中,=0.6826
=0.9544,=0.9974.
选择题:(本大题共10小题,每小题3分,共30分.)
1、某种彩票中奖概率为0.2%,有人买了1000张彩票,下列说法正确的是…………( )
A、此人不可能中奖 B、此人一定有2张彩票中奖
C、每张彩票中奖的可能性都相等 D、最后买的几张彩票中奖的可能性大些
2、在某次数学考试中,考生的成绩服从正态分布N(90,100),则考试成绩在110分以上的概率是………………………………………………( )
A、0.1587 B、0.0228 C、0.0456 D、不能确定
3、在抽查某产品的尺寸过程中,将其尺寸等距分成若干组,[m,n)是其中一组,若抽出的样本在该组上的频率为a,频率分布直方图中该组矩形的高为h,则|m-n|等于………………( )
A、h·a B、 C、 D、与a,h无关
4、用秦九韶算法计算,要用到的乘法和加法的次数分别是( )
A、3次,3次 B、4次,4次 C、4次,3次 D、3次,4次
5、如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知………………………………………………………………( )
A、甲运动员的最低得分为0分;
B、乙运动员得分的中位数是29;
C、甲运动员得分的众数为44 ;
D、乙运动员得分的平均值在区间(11,19)内.
6、一个幼儿园的母亲节联谊会上,有5个小孩分别给妈妈画了一幅画作为礼物,放在了5个相同的信封里,可是忘了做标记,现在妈妈们随机的任取一个信封,则恰好有两个妈妈拿到了自己孩子的画的情况共有…………………………( )
A、30种 B、20种 C、15种 D、10种
7、分别抛掷2枚质地均匀的硬币,设A是事件“第1枚为正面”,B是事件“第2枚为正面”,C为事件“2枚结果相同”,则事件A与B,A与C,B与C中相互独立的事件有
A、0对 B、1对 C、2对 D、3对
8、设,则除以9的余数为……………………( )
A、0 B、2 C、 7 D、0或7
9、下列说法不正确的是………………………………………………( )
A、残差平方和越大,预报精确度越高;
B、在独立检验中,通过二维条形图和三维柱形图可以粗略地判断两个分类变量是否有关系,但是这种判断无法精确地给出所得结论的可靠程度;
C、对于分类变量X与Y的随机变量的观测值k,k越小,则“X与Y有关系”可信度越小;
D、设有一个回归方程,若变量x每增加一个单位时,y平均减少1.5单位.
10、将甲、乙两颗骰子先后各抛掷一次,a,b分别表示抛掷甲、乙两颗骰子所掷出的点数,若M(a,b)落在不等式≤m(m为常数)所表示的区域内,设为事件C,要使事件C的概率P(C)=,则实数m的最小值为…………( )
A、52 B、51 C、45 D、41
二、填空题:(本大题共7小题,每小题4分,共28分.把答案填在题中横线上.)
11、已知,=8,=1.6,则p= .
12、设随机变量的概率分布为P(=k)=,(k=0,1,2),则实数C= .
13、若把十进制数87化成四进制数,则该四进制数的末位为 .
14、的展开式的第6项的系数是 (用数字作答).
15、下面程序运行后输出的结果为 .
16、一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k(2≤k≤10)组中抽取的号码个位数字与m×k的个位数字相同,若m=6,则在第7组中抽取的号码是 .
17、甲、乙两艘轮船都要在某个泊位停靠,甲停靠时间为8小时,乙停靠时间为4小时,假定它们在一昼夜的时间段中随机地到达,则这两艘船在停靠泊位时不需要等待的概率为 .
三、解答题:(本大题共5小题,共42分.解答应写出文字说明、证明过程或演算步骤.)
18、(本小题6分)用数字0,1,2,3,4组成没有重复数字的数.
(1)能够组成多少个五位数? (2)能够组成多少个五位奇数?
(3)能够组成多少个正整数?(以上最后结果用数字作答)
x
2
4
5
6
8
y
30
40
50
60
70
19、(本小题8分)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系,
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
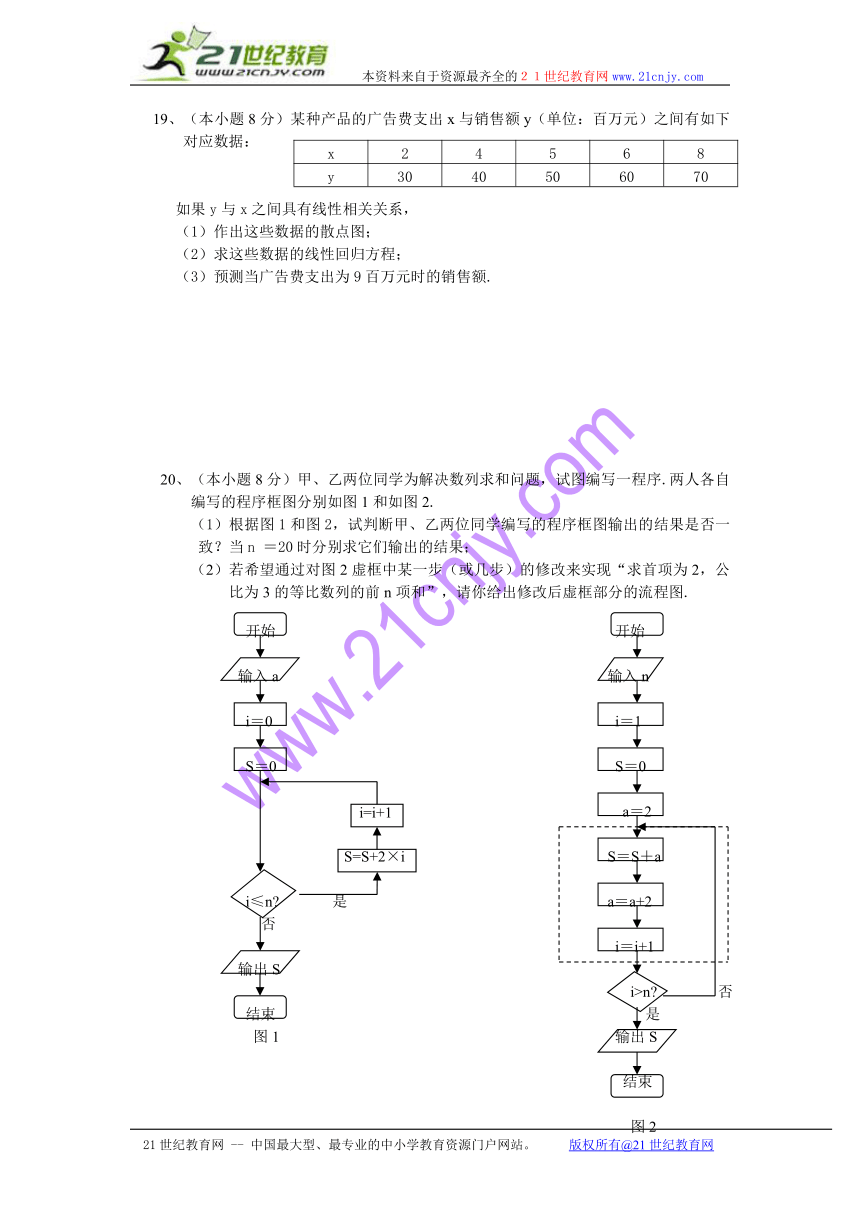
20、(本小题8分)甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图1和如图2.
(1)根据图1和图2,试判断甲、乙两位同学编写的程序框图输出的结果是否一致?当n =20时分别求它们输出的结果;
(2)若希望通过对图2虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的流程图.
21、(本小题10分)在一个盒子中,放有标号分别为2,3,4的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别 x、y,记.
(1)求随机变量的所有取值;(2)求随机变量的分布列;
(3)求随机变量的数学期望和方差.
22、(本小题10分)现有甲、乙两个盒子,甲盒中装有4个白球和4个红球,乙盒中装有3个白球和若干个红球,若从乙盒中任取两个球,取到两个白球的概率是.
(1)求乙盒中红球的个数;
(2)从甲盒中任取两个球,在所取的球中有一个是白球的条件下,求另一个也是白球的概率;
(3)若从甲盒中任取两个球,放入乙盒中后,再从乙盒中任意取出2个球放回到甲盒中,求甲盒中白球没有增加的概率.
龙高高二数学(理)期末模拟试卷参考答案
一、选择题:(每小题3分,共30分)
1
2
3
4
5
6
7
8
9
10
C
B
B
A
C
B
D
D
A
C
二、填空题:(每小题4分,共28分)
11、0.8; 12、; 13、3; 14、-56; 15、11; 16、62; 17、.
三、解答题:(本大题共5小题,共52分.解答应写出文字说明、证明过程或演算步骤.)
18、解:(1)=96 (2)=36
(3)=260
19、解:(1)图2分(2)=5,=50,=1390, =145 4分
=7,=15. ∴线性回归方程为=7x+15 6分
(3)当x=9时,=78 8分
20、解:(1)输出结果一致。 1分
n=20时,
图1的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 3分
图2的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 5分
(2)修改后虚框部分的流程图为
8分
S=S+a a=3﹡a i=i+1
21、解:(1)∵x、y可能的取值为2、3、4,∴的所有取值为0,1,2,3. 2 分
(2)的所有取值为0,1,2,3.∵=0时,只有x=3,y=3这一种情况,
=1时,只有x=2,y=2或x=3,y=2或x=3,y=4或x=4,y=4四种情况,
=2时,只有x=2,y=3或x=4,y=3两种情况,
=3时,只有x=2,y=4或x=4,y=2两种情况.
∴P(=0)=,P(=1)=,P(=2)=,P(=3)=.
则随机变量的分布列为:
0
1
2
3
P
8分
(3)数学期望==
=+= 10分
22、解:(1)设乙盒中有n个红球,则=,n=5,即乙盒中有5个红球3分
(2)设A=“有一个是白球”,B=“另一个也是白球”,
则P(B|A)===; 6分
(3)法1:若甲盒中白球增加了,则有以下两种情况:
①从甲盒中取出了2个红球,放入乙盒中均匀后从乙盒中取出两个白球或1个白球1个红球放入甲盒中,此时的概率是=;
②从甲盒中取出了1个白球1个红球,放入乙盒中均匀后从乙盒中取出两个白球放入甲盒中,此时的概率是=
甲盒中白球增加了的概率为+=,所以甲盒中白球没有增加的概率为.10分
法2:直接法:若甲盒中白球没有增加,则有以下三种情况:
从甲盒中取出了2个红球,放入乙盒中均匀后从乙盒中取出两个红球放入甲盒中,此时的概率是;②从甲盒中取出了1个白球1个红球,放入乙盒中均匀后从乙盒中取出两个红球或1个白球1个红球放入甲盒中,此时的概率是;③从甲盒中取出了2个白球,放入乙盒中均匀后从乙盒中取出两个白球或1个白球1个红球或2个红球放入甲盒中,此时的概率是
所以甲盒中白球没有增加的概率为. 10分
参考公式和数据:
用最小二乘法求线性回归直线方程系数公式,.
正态分布中,=0.6826
=0.9544,=0.9974.
选择题:(本大题共10小题,每小题3分,共30分.)
1、某种彩票中奖概率为0.2%,有人买了1000张彩票,下列说法正确的是…………( )
A、此人不可能中奖 B、此人一定有2张彩票中奖
C、每张彩票中奖的可能性都相等 D、最后买的几张彩票中奖的可能性大些
2、在某次数学考试中,考生的成绩服从正态分布N(90,100),则考试成绩在110分以上的概率是………………………………………………( )
A、0.1587 B、0.0228 C、0.0456 D、不能确定
3、在抽查某产品的尺寸过程中,将其尺寸等距分成若干组,[m,n)是其中一组,若抽出的样本在该组上的频率为a,频率分布直方图中该组矩形的高为h,则|m-n|等于………………( )
A、h·a B、 C、 D、与a,h无关
4、用秦九韶算法计算,要用到的乘法和加法的次数分别是( )
A、3次,3次 B、4次,4次 C、4次,3次 D、3次,4次
5、如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,中间的数字表示得分的十位数,据图可知………………………………………………………………( )
A、甲运动员的最低得分为0分;
B、乙运动员得分的中位数是29;
C、甲运动员得分的众数为44 ;
D、乙运动员得分的平均值在区间(11,19)内.
6、一个幼儿园的母亲节联谊会上,有5个小孩分别给妈妈画了一幅画作为礼物,放在了5个相同的信封里,可是忘了做标记,现在妈妈们随机的任取一个信封,则恰好有两个妈妈拿到了自己孩子的画的情况共有…………………………( )
A、30种 B、20种 C、15种 D、10种
7、分别抛掷2枚质地均匀的硬币,设A是事件“第1枚为正面”,B是事件“第2枚为正面”,C为事件“2枚结果相同”,则事件A与B,A与C,B与C中相互独立的事件有
A、0对 B、1对 C、2对 D、3对
8、设,则除以9的余数为……………………( )
A、0 B、2 C、 7 D、0或7
9、下列说法不正确的是………………………………………………( )
A、残差平方和越大,预报精确度越高;
B、在独立检验中,通过二维条形图和三维柱形图可以粗略地判断两个分类变量是否有关系,但是这种判断无法精确地给出所得结论的可靠程度;
C、对于分类变量X与Y的随机变量的观测值k,k越小,则“X与Y有关系”可信度越小;
D、设有一个回归方程,若变量x每增加一个单位时,y平均减少1.5单位.
10、将甲、乙两颗骰子先后各抛掷一次,a,b分别表示抛掷甲、乙两颗骰子所掷出的点数,若M(a,b)落在不等式≤m(m为常数)所表示的区域内,设为事件C,要使事件C的概率P(C)=,则实数m的最小值为…………( )
A、52 B、51 C、45 D、41
二、填空题:(本大题共7小题,每小题4分,共28分.把答案填在题中横线上.)
11、已知,=8,=1.6,则p= .
12、设随机变量的概率分布为P(=k)=,(k=0,1,2),则实数C= .
13、若把十进制数87化成四进制数,则该四进制数的末位为 .
14、的展开式的第6项的系数是 (用数字作答).
15、下面程序运行后输出的结果为 .
16、一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k(2≤k≤10)组中抽取的号码个位数字与m×k的个位数字相同,若m=6,则在第7组中抽取的号码是 .
17、甲、乙两艘轮船都要在某个泊位停靠,甲停靠时间为8小时,乙停靠时间为4小时,假定它们在一昼夜的时间段中随机地到达,则这两艘船在停靠泊位时不需要等待的概率为 .
三、解答题:(本大题共5小题,共42分.解答应写出文字说明、证明过程或演算步骤.)
18、(本小题6分)用数字0,1,2,3,4组成没有重复数字的数.
(1)能够组成多少个五位数? (2)能够组成多少个五位奇数?
(3)能够组成多少个正整数?(以上最后结果用数字作答)
x
2
4
5
6
8
y
30
40
50
60
70
19、(本小题8分)某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系,
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
20、(本小题8分)甲、乙两位同学为解决数列求和问题,试图编写一程序.两人各自编写的程序框图分别如图1和如图2.
(1)根据图1和图2,试判断甲、乙两位同学编写的程序框图输出的结果是否一致?当n =20时分别求它们输出的结果;
(2)若希望通过对图2虚框中某一步(或几步)的修改来实现“求首项为2,公比为3的等比数列的前n项和”,请你给出修改后虚框部分的流程图.
21、(本小题10分)在一个盒子中,放有标号分别为2,3,4的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别 x、y,记.
(1)求随机变量的所有取值;(2)求随机变量的分布列;
(3)求随机变量的数学期望和方差.
22、(本小题10分)现有甲、乙两个盒子,甲盒中装有4个白球和4个红球,乙盒中装有3个白球和若干个红球,若从乙盒中任取两个球,取到两个白球的概率是.
(1)求乙盒中红球的个数;
(2)从甲盒中任取两个球,在所取的球中有一个是白球的条件下,求另一个也是白球的概率;
(3)若从甲盒中任取两个球,放入乙盒中后,再从乙盒中任意取出2个球放回到甲盒中,求甲盒中白球没有增加的概率.
龙高高二数学(理)期末模拟试卷参考答案
一、选择题:(每小题3分,共30分)
1
2
3
4
5
6
7
8
9
10
C
B
B
A
C
B
D
D
A
C
二、填空题:(每小题4分,共28分)
11、0.8; 12、; 13、3; 14、-56; 15、11; 16、62; 17、.
三、解答题:(本大题共5小题,共52分.解答应写出文字说明、证明过程或演算步骤.)
18、解:(1)=96 (2)=36
(3)=260
19、解:(1)图2分(2)=5,=50,=1390, =145 4分
=7,=15. ∴线性回归方程为=7x+15 6分
(3)当x=9时,=78 8分
20、解:(1)输出结果一致。 1分
n=20时,
图1的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 3分
图2的结果为2+4+6+…+38+40=2×(1+2+3+…+20)=420 5分
(2)修改后虚框部分的流程图为
8分
S=S+a a=3﹡a i=i+1
21、解:(1)∵x、y可能的取值为2、3、4,∴的所有取值为0,1,2,3. 2 分
(2)的所有取值为0,1,2,3.∵=0时,只有x=3,y=3这一种情况,
=1时,只有x=2,y=2或x=3,y=2或x=3,y=4或x=4,y=4四种情况,
=2时,只有x=2,y=3或x=4,y=3两种情况,
=3时,只有x=2,y=4或x=4,y=2两种情况.
∴P(=0)=,P(=1)=,P(=2)=,P(=3)=.
则随机变量的分布列为:
0
1
2
3
P
8分
(3)数学期望==
=+= 10分
22、解:(1)设乙盒中有n个红球,则=,n=5,即乙盒中有5个红球3分
(2)设A=“有一个是白球”,B=“另一个也是白球”,
则P(B|A)===; 6分
(3)法1:若甲盒中白球增加了,则有以下两种情况:
①从甲盒中取出了2个红球,放入乙盒中均匀后从乙盒中取出两个白球或1个白球1个红球放入甲盒中,此时的概率是=;
②从甲盒中取出了1个白球1个红球,放入乙盒中均匀后从乙盒中取出两个白球放入甲盒中,此时的概率是=
甲盒中白球增加了的概率为+=,所以甲盒中白球没有增加的概率为.10分
法2:直接法:若甲盒中白球没有增加,则有以下三种情况:
从甲盒中取出了2个红球,放入乙盒中均匀后从乙盒中取出两个红球放入甲盒中,此时的概率是;②从甲盒中取出了1个白球1个红球,放入乙盒中均匀后从乙盒中取出两个红球或1个白球1个红球放入甲盒中,此时的概率是;③从甲盒中取出了2个白球,放入乙盒中均匀后从乙盒中取出两个白球或1个白球1个红球或2个红球放入甲盒中,此时的概率是
所以甲盒中白球没有增加的概率为. 10分
