物理人教版(2019)选择性必修第一册4.1光的折射(共43张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册4.1光的折射(共43张ppt) |
|
|
| 格式 | pptx | ||
| 文件大小 | 27.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览






文档简介
(共43张PPT)
新课导入:
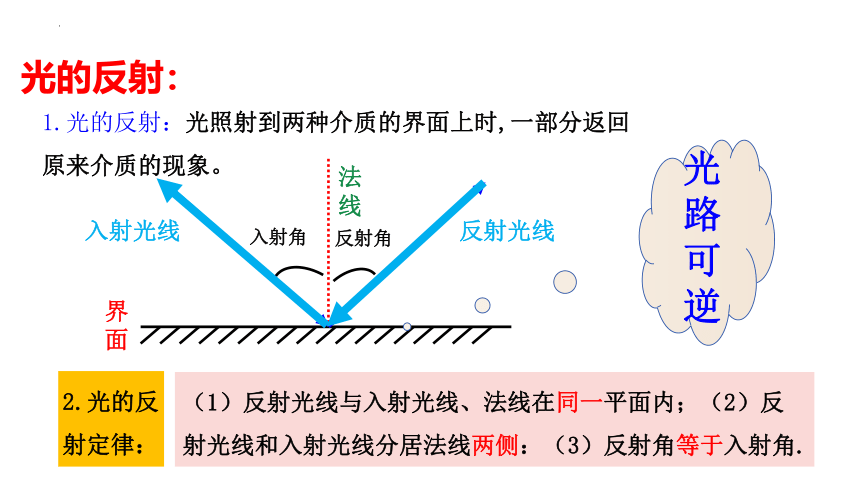
观察图片思考以下问题:
1、当光从玻璃射入空气时,传播方向发生了怎样的改变?
2、在反射现象中,光的传播遵从怎样的规律呢?
3、在折射现象中,光的传播遵从怎样的规律呢?
界面
入射光线
反射光线
法线
入射角
反射角
1.光的反射:光照射到两种介质的界面上时,一部分返回原来介质的现象。
(1)反射光线与入射光线、法线在同一平面内;(2)反射光线和入射光线分居法线两侧:(3)反射角等于入射角.
光路可逆
2.光的反射定律:
光的反射:
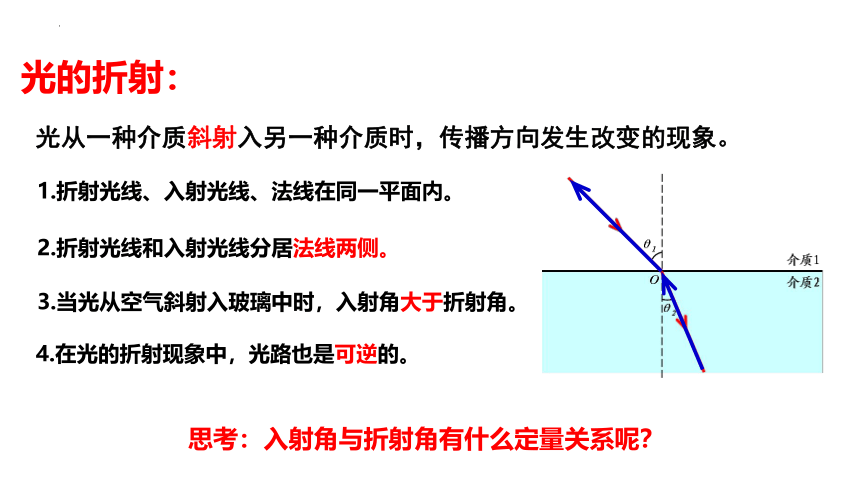
1.折射光线、入射光线、法线在同一平面内。
2.折射光线和入射光线分居法线两侧。
3.当光从空气斜射入玻璃中时,入射角大于折射角。
4.在光的折射现象中,光路也是可逆的。
思考:入射角与折射角有什么定量关系呢?
光的折射:
光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
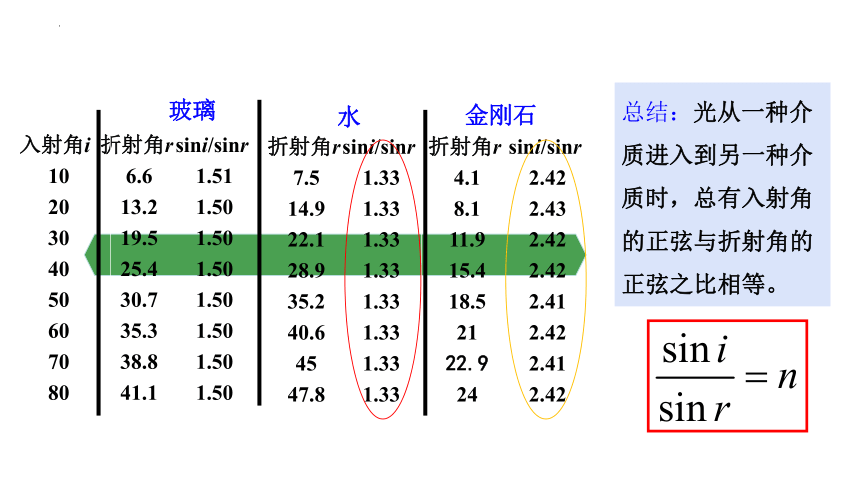
=n(n为常数)
实验结论:入射角的正弦跟折射角的正弦成正比
以光从空气射入玻璃为例
折射角和入射角的关系
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者
之间的关系,并把它总结为光的折射定律(refraction law):
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
光的折射:
n12与入射角、折射角大小无关,只与两种介质的性质有关
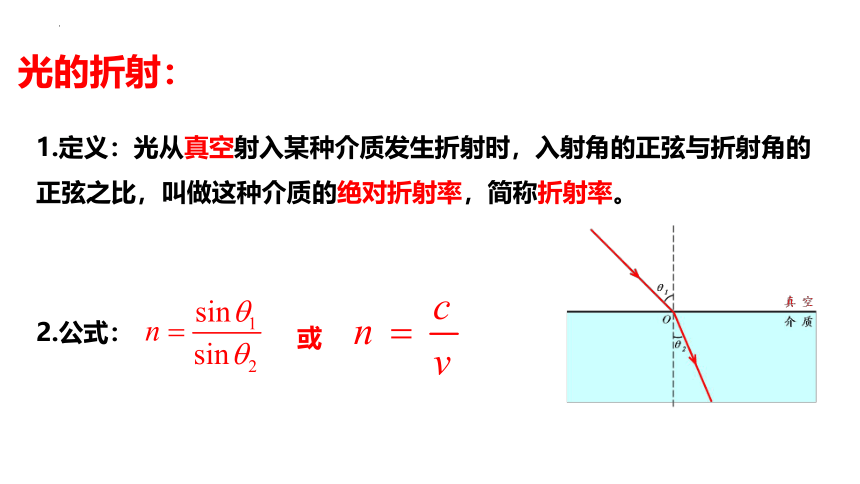
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。
2.公式:
或
光的折射:
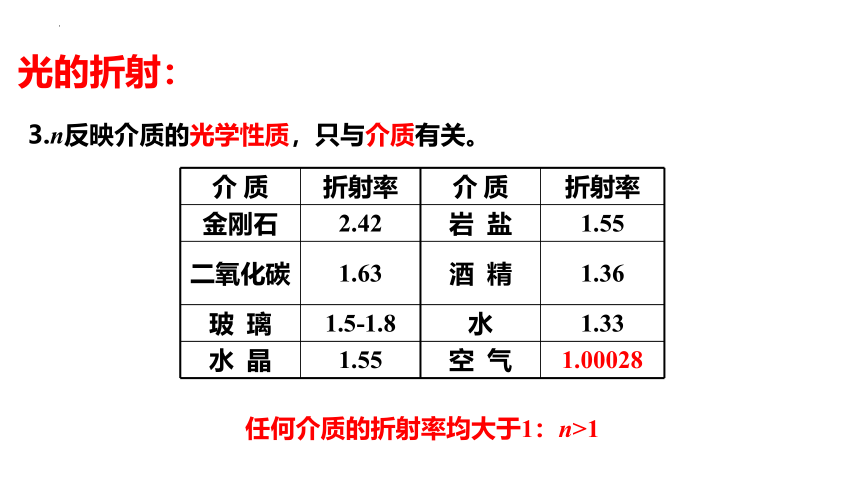
3.n反映介质的光学性质,只与介质有关。
任何介质的折射率均大于1:n>1
介 质 折射率 介 质 折射率
金刚石 2.42 岩 盐 1.55
二氧化碳 1.63 酒 精 1.36
玻 璃 1.5-1.8 水 1.33
水 晶 1.55 空 气 1.00028
光的折射:
4.折射率无单位。
5.折射率n越大,光线偏折越大。
6.当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
光的折射:
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶低上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
解:
解决光的反射、折射问题的方法:
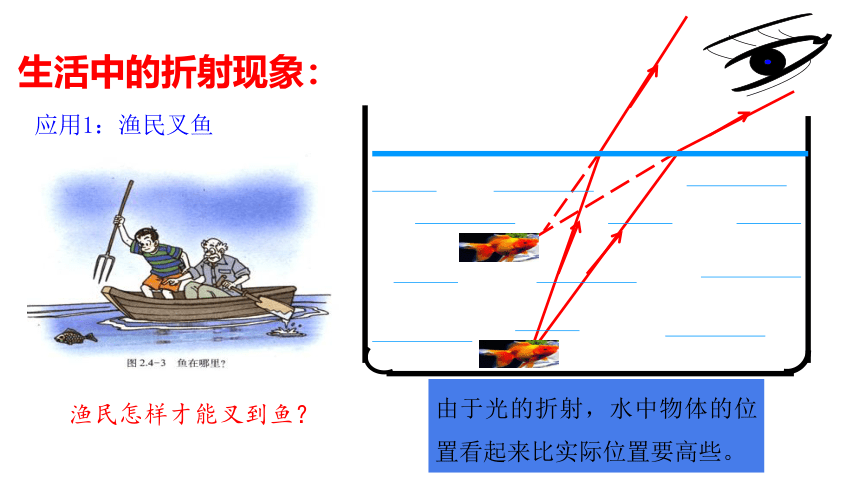
由于光的折射,水中物体的位置看起来比实际位置要高些。
应用1:渔民叉鱼
渔民怎样才能叉到鱼?
生活中的折射现象:
高
水
看到的气球在折射光线的反向延长线上.
空气
应用2:在水下看水面上的物体比实际位置高还是低?
生活中的折射现象:
应用3:铅笔弯折之谜
空气
水
A
A
界面
生活中的折射现象:
应用4:井中的青蛙看岸上的物体的位置偏向哪里?
偏向上方
井中的青蛙看井口的宽度是偏大还是偏小?
偏小
生活中的折射现象:
SS′有大气,看到太阳更早没有大气,将迟一些看到太阳应用5:蒙气差现象生活中的折射现象:1、如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
【正确答案】C
2、光在某种玻璃中的传播速度是 ,要使光由玻璃射入空气时折射光线与反射光线成90°,则入射光线与反射光线的夹角成( )
A.30° B.60° C.45° D.90°
【正确答案】B
B
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
测定玻璃的折射率:
一、实验目的
掌握测量玻璃折射率的方法。
二、实验设计
1.实验方案
如图当光以一定的入射角透过一块两面平行的玻璃砖时,只要找出与入射光线AO相对应的出射光线O′D就能够画出光从空气射入玻璃后的折射光线OO′,于是就能测量入射角θ1、折射角θ2。根据折射定律,就可以求出玻璃的折射率了。
三、实验步骤
1.如图所示,将白纸用图钉钉在平木板上。
2.在白纸上画出一条直线aa′作为界面(线)。过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
3.把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
4.在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
5.移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
6.连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角,从三角函数表中查出它们的正弦值,把这些数据记录在自己设计的表格中。
测定玻璃的折射率
1.图象法:
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
四、数据处理
2.作图法:
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 ,且CO=DO,所以折射率 。
四、数据处理
五、注意事项
1.实验时,尽可能将大头针竖直插在纸上,且大头针之间及大头针与光线转折点之间的距离要稍大一些。
2.入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大。
3.在操作时,手不能触摸玻璃砖的光学面。更不能把玻璃砖界面当尺子画界线。
4.在实验过程中,玻璃砖与白纸的相对位置不能改变。
5.玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
六、实验误差
1.入射光线和出射光线确定的不够精确。因此要求插大头针时两大头针间距应稍大。
2.入射角、折射角测量的不精确。为减小测角时的相对误差,入射角要稍大些,但不宜太大,入射角太大时,反射光较强,折射光会相对较弱。
D
C
3、有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最小
D.光在介质C中的速度最大
B
4、光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直。(真空中的光速c=3.0×108 m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度大小;
(3)当入射角变为45°时,折射角的正弦值是多大
(4)当入射角增大或减小时,玻璃的折射率是否变化
【解析】 (1)由题意知入射角θ1=60°,反射角θ'=60°,折射角
θ2=180°-60°-90°=30°,光路图如图所示。
(4)折射率不会变化,折射率由介质和入射光线的频率决定,跟入射角的大小无关。
5、如图所示,一束激光垂直于AC面照射到等边玻璃三棱镜的AB面上。已知AB面的反射光线与折射光线的夹角为90°。光在真空中的传播速度为c。求:(1)玻璃的折射率;
(2)激光在玻璃中传播的速度。
1.常规思路
(1)根据题意画出正确的光路图.
(2)利用几何关系确定光路图中的边、角关系,要注意入射角、折射角均是与法线的夹角.
(3)利用折射定律、折射率公式列式求解.
解决光的折射问题的常规思路
2.视深问题
(1)视深是人眼看透明物质内部某物点时像点离界面的距离.在中学阶段,一般都是沿着界面的法线方向去观察,在计算时,由于入射角很小,折射角也很小,故有 ,这是在视深问题中经常用到的关系式.
(2)当沿竖直方向看水中物体时,“视深”是实际深度的n倍,n是水的折射率.
解决光的折射问题的视深问题
新课导入:
观察图片思考以下问题:
1、当光从玻璃射入空气时,传播方向发生了怎样的改变?
2、在反射现象中,光的传播遵从怎样的规律呢?
3、在折射现象中,光的传播遵从怎样的规律呢?
界面
入射光线
反射光线
法线
入射角
反射角
1.光的反射:光照射到两种介质的界面上时,一部分返回原来介质的现象。
(1)反射光线与入射光线、法线在同一平面内;(2)反射光线和入射光线分居法线两侧:(3)反射角等于入射角.
光路可逆
2.光的反射定律:
光的反射:
1.折射光线、入射光线、法线在同一平面内。
2.折射光线和入射光线分居法线两侧。
3.当光从空气斜射入玻璃中时,入射角大于折射角。
4.在光的折射现象中,光路也是可逆的。
思考:入射角与折射角有什么定量关系呢?
光的折射:
光从一种介质斜射入另一种介质时,传播方向发生改变的现象。
入射角i
10
30
40
50
60
70
80
折射角r
6.6
19.5
25.4
30.7
35.3
38.8
41.1
i / r
1.51
1.54
1.57
1.63
1.70
1.80
1.95
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
=n(n为常数)
实验结论:入射角的正弦跟折射角的正弦成正比
以光从空气射入玻璃为例
折射角和入射角的关系
思考:如果将玻璃换成其它介质,入射角和折射角的正弦之比是否具有相同的结论?
sini/sinr
1.51
1.50
1.50
1.50
1.50
1.50
1.50
1.50
入射角i
10
20
30
40
50
60
70
80
折射角r
6.6
13.2
19.5
25.4
30.7
35.3
38.8
41.1
玻璃
水
折射角r
7.5
14.9
22.1
28.9
35.2
40.6
45
47.8
sini/sinr
1.33
1.33
1.33
1.33
1.33
1.33
1.33
1.33
金刚石
折射角r
4.1
8.1
11.9
15.4
18.5
21
22.9
24
sini/sinr
2.42
2.43
2.42
2.42
2.41
2.42
2.41
2.42
总结:光从一种介质进入到另一种介质时,总有入射角的正弦与折射角的正弦之比相等。
斯涅耳
1621 年,荷兰数学家斯涅耳在分析了大量实验数据后,找到了两者
之间的关系,并把它总结为光的折射定律(refraction law):
入射光线、法线处在同一平面内,折射光线与入射光线分别位于法线的两侧;入射角的正弦与折射角的正弦成正比,即:
光的折射:
n12与入射角、折射角大小无关,只与两种介质的性质有关
1.定义:光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,简称折射率。
2.公式:
或
光的折射:
3.n反映介质的光学性质,只与介质有关。
任何介质的折射率均大于1:n>1
介 质 折射率 介 质 折射率
金刚石 2.42 岩 盐 1.55
二氧化碳 1.63 酒 精 1.36
玻 璃 1.5-1.8 水 1.33
水 晶 1.55 空 气 1.00028
光的折射:
4.折射率无单位。
5.折射率n越大,光线偏折越大。
6.当光从折射率小的介质斜射入折射率大的介质时,入射角大于折射角,当光从折射率大的介质斜射入折射率小的介质时,入射角小于折射角。
光的折射:
【例题】如图一个储油桶的底面直径与高均为d.当桶内没有油时,从某点A恰能看到桶底边缘的某点B。当桶内油的深度等于桶高的一半时,仍沿AB方向看去,恰好看到桶低上的点C,CB两点距离d/4.求油的折射率和光在油中传播的速度。
B
A
d
C
O
D
N
Nˊ
θ2
解:
解决光的反射、折射问题的方法:
由于光的折射,水中物体的位置看起来比实际位置要高些。
应用1:渔民叉鱼
渔民怎样才能叉到鱼?
生活中的折射现象:
高
水
看到的气球在折射光线的反向延长线上.
空气
应用2:在水下看水面上的物体比实际位置高还是低?
生活中的折射现象:
应用3:铅笔弯折之谜
空气
水
A
A
界面
生活中的折射现象:
应用4:井中的青蛙看岸上的物体的位置偏向哪里?
偏向上方
井中的青蛙看井口的宽度是偏大还是偏小?
偏小
生活中的折射现象:
SS′有大气,看到太阳更早没有大气,将迟一些看到太阳应用5:蒙气差现象生活中的折射现象:1、如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
【正确答案】C
2、光在某种玻璃中的传播速度是 ,要使光由玻璃射入空气时折射光线与反射光线成90°,则入射光线与反射光线的夹角成( )
A.30° B.60° C.45° D.90°
【正确答案】B
B
玻璃是一种透明介质,光从空气入射到玻璃的界面上会发生折射,如何把玻璃的折射率测出来?
测定玻璃的折射率:
一、实验目的
掌握测量玻璃折射率的方法。
二、实验设计
1.实验方案
如图当光以一定的入射角透过一块两面平行的玻璃砖时,只要找出与入射光线AO相对应的出射光线O′D就能够画出光从空气射入玻璃后的折射光线OO′,于是就能测量入射角θ1、折射角θ2。根据折射定律,就可以求出玻璃的折射率了。
三、实验步骤
1.如图所示,将白纸用图钉钉在平木板上。
2.在白纸上画出一条直线aa′作为界面(线)。过aa′上的一点O画出界面的法线NN′,并画一条线段AO作为入射光线。
3.把长方形玻璃砖放在白纸上,使它的长边跟aa′对齐,画出玻璃砖的另一边bb′。
4.在直线AO上竖直插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,调整视线方向直到P2的像挡住P1的像。再在观察者一侧竖直插上两枚大头针P3、P4,使P3挡住P1、P2的像,P4挡住P3及P1、P2的像,记下P3、P4的位置。
5.移去大头针和玻璃砖,过P3、P4所在处作直线O′B与bb′交于O′,直线O′B就代表了沿AO方向入射的光线通过玻璃砖后的传播方向。
6.连接OO′,入射角θ1=∠AON,折射角θ2=∠O′ON′,用量角器量出入射角和折射角,从三角函数表中查出它们的正弦值,把这些数据记录在自己设计的表格中。
测定玻璃的折射率
1.图象法:
以sin θ1值为横坐标、以sinθ2值为纵坐标,建立直角坐标系,如图所示。描数据点,过数据点连线得一条过原点的直线。求解图线斜率k,则 ,故玻璃砖折射率 。
四、数据处理
2.作图法:
在找到入射光线和折射光线以后,以入射点O为圆心,以任意长为半径画圆,分别与AO交于C点、OO′(或OO′的延长线)交于D点,过C、D两点分别向NN′作垂线,交NN′于C′、D′,用直尺量出CC′和DD′的长,如图 2所示。由于 ,且CO=DO,所以折射率 。
四、数据处理
五、注意事项
1.实验时,尽可能将大头针竖直插在纸上,且大头针之间及大头针与光线转折点之间的距离要稍大一些。
2.入射角θ1应适当大一些,以减小测量角度的误差,但入射角不宜太大。
3.在操作时,手不能触摸玻璃砖的光学面。更不能把玻璃砖界面当尺子画界线。
4.在实验过程中,玻璃砖与白纸的相对位置不能改变。
5.玻璃砖应选用宽度较大的,宜在5 cm以上。若宽度太小,则测量误差较大。
六、实验误差
1.入射光线和出射光线确定的不够精确。因此要求插大头针时两大头针间距应稍大。
2.入射角、折射角测量的不精确。为减小测角时的相对误差,入射角要稍大些,但不宜太大,入射角太大时,反射光较强,折射光会相对较弱。
D
C
3、有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大
B.介质C的折射率最大
C.光在介质B中的速度最小
D.光在介质C中的速度最大
B
4、光线以60°的入射角从空气射入玻璃中,折射光线与反射光线恰好垂直。(真空中的光速c=3.0×108 m/s)
(1)画出折射光路图;
(2)求出玻璃的折射率和光在玻璃中的传播速度大小;
(3)当入射角变为45°时,折射角的正弦值是多大
(4)当入射角增大或减小时,玻璃的折射率是否变化
【解析】 (1)由题意知入射角θ1=60°,反射角θ'=60°,折射角
θ2=180°-60°-90°=30°,光路图如图所示。
(4)折射率不会变化,折射率由介质和入射光线的频率决定,跟入射角的大小无关。
5、如图所示,一束激光垂直于AC面照射到等边玻璃三棱镜的AB面上。已知AB面的反射光线与折射光线的夹角为90°。光在真空中的传播速度为c。求:(1)玻璃的折射率;
(2)激光在玻璃中传播的速度。
1.常规思路
(1)根据题意画出正确的光路图.
(2)利用几何关系确定光路图中的边、角关系,要注意入射角、折射角均是与法线的夹角.
(3)利用折射定律、折射率公式列式求解.
解决光的折射问题的常规思路
2.视深问题
(1)视深是人眼看透明物质内部某物点时像点离界面的距离.在中学阶段,一般都是沿着界面的法线方向去观察,在计算时,由于入射角很小,折射角也很小,故有 ,这是在视深问题中经常用到的关系式.
(2)当沿竖直方向看水中物体时,“视深”是实际深度的n倍,n是水的折射率.
解决光的折射问题的视深问题
