苏教版六年级下册数学第六单元《正比例和反比例》检测卷(含解析)
文档属性
| 名称 | 苏教版六年级下册数学第六单元《正比例和反比例》检测卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 320.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 00:00:00 | ||
图片预览



文档简介
六年级数学下册单元检测卷
第六单元《正比例和反比例》
姓名:_________ 班级:_________ 学号:_________
(时间:60分钟 分值:100分)
一、填空。(每空1分,共16分)
1.路程和时间是两种相关联的量,当它们的比值(速度)保持一定时,路程和时间是成( )比例的量,它们的关系是( )比例关系。
2.每袋面粉的质量一定,面粉的总质量和袋数成( )比例。
3.总价一定,单价和数量成( )比例.
4.路程一定,速度和时间成( )。
5.总人数一定,每行站的人数与站的行数成( )比例。
6.每天耕地的公顷数一定,耕地的天数和耕地的公顷数成( )比例。
7.正比例的图像是一条( )。
8.判断下面各题中的两种量是否成比例,如果成比例,成什么比例。
(1)长方体的体积一定,它的底面积和高。( )
(2)三角形的面积一定,它的底和高。( )
(3)铺地的面积一定,所用方砖的边长和所需块数。( )
(4)圆的周长和它的半径。( )
(5)圆的面积和它的半径。( )
(6)修一条公路,已修好的长度与未修好的长度。( )
9.当速度一定时,路程与时间成( )比例;当时间一定时,速度与路程成( )比例。
二、判断题。(对的在括号里画“√”,错的画“×”)(每小题1分,共10分)
10.气温与月份成正比例。( )
11.任何一个非0自然数,与它的倒数成反比例。( )
12.比的前项一定,比的后项和比值成正比例。( )
13.两种相关联的量,如果相对应的两个数一定,这两种量成正比例。( )
14.车轮的直径一定,所行路程与车轮转的周数成正比例。( )
15.一本书的总页数一定,已读的页数和未读的页数成反比例。( )
16.零件总数一定,每小时加工的个数和加工时间成反比例。( )
17.工作总量一定,工作时间和工作效率成反比例。( )
18.圆的周长一定,圆周率和半径成反比例。______
19.长方形的宽一定,它的面积和长成正比例。( )
三、精挑细选。(把正确答案的序号填在括号里)(每小题2分,共20分)
20.下面每组的两个量中,成正比例关系的是( )。
A.长方形的面积一定,长和宽 B.一个人的年龄和头发长度
C.时间一定,路程和速度 D.男生人数一定,女生人数和全班人数
21.爸爸和儿子两人的年龄( )。
A.成正比例 B.成反比例 C.不成比例
22.如果5x=y,那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
23.已知a∶b=4∶5,那么a和b( )。
A.不成比例 B.成反比例 C.成正比例
24.三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量( )。
A.成正比例 B.成反比例 C.不成比例
25.表示x和y成反比例的式子是( )。
A.x+y=100 B.xy=35 C.x/y=8
26.苹果的总质量一定,每箱苹果的质量和箱数( )。
A.成正比例 B.成反比例 C.不成比例
27.圆柱的体积一定,底面积和高( )
A.成正比例 B.成反比例 C.不成比例
28.每小时加工20个零件,加工零件的总数与加工时间( )。
A.成正比例 B.成反比例 C.不成比例
29.已知xy=k+,k一定时,x和y( )。
A.成正比例 B.成反比例 C.不成比例
30.一辆汽车行驶的时间和所行的路程如下表,看表填空。
时间/时 1 2 3 4 5 6 7 8 9 …
路程/千米 50 100 150 200 250 300 350 400 450 …
(1)表中相关联的两种量是( )和( )。
(2)时间扩大时,路程也( );时间缩小时,路程也( )。它们扩大或缩小规律是:路程和时间相对应的两个量的比值( ),也就是( )一定。
(3)在路程、时间、速度三者之间存在着=速度(一定)数量关系,这就是说速度一定,路程与时间成( )比例。
31.解比例。
7.5∶x=2.5∶12 ∶=x∶15
2.25+3x= 3.5∶x=0.7∶1.2 ∶x∶
32.根据正比例或反比例的关系填写下表。
(1)已知表中的x与y成正比例关系,请完成下表。
x 2 4 8 ( ) ( ) 64
y ( ) ( ) 56 112 168 ( )
(2)已知表中的x与y成反比例关系,请完成下表。
x 2 4 8 ( ) ( ) ( )
y ( ) ( ) 56 112 224 448
七、解决问题。(共25分)
33.一台织布机织布的时间和织布的米数如下表:
时间/时 1 2 3 4 5 6 7 8 9 …
织布的米数/米 15 30 45 60 75 90 105 120 135 …
(1)上表中的两种量的变化有什么规律?
(2)上表中两种量成什么比例关系?
(3)如果织布总米数一定,那么时间和每小时织布的数量成什么比例关系?
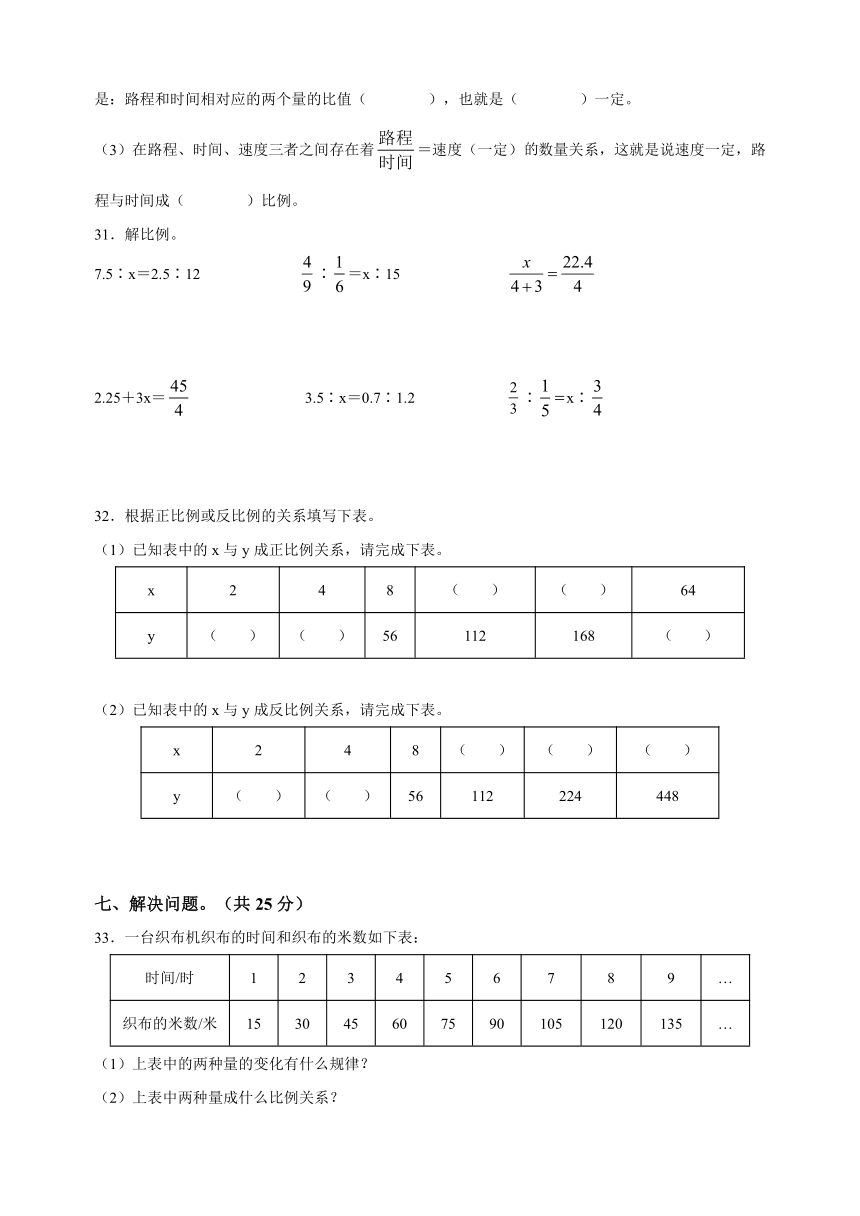
34.下图中比例尺是1∶200000,算出图中标出的点的实际距离。
35.一辆汽车准备从甲地开往乙地。根据下表提供的信息,把表格填写完整。
时间/时 8 10 16 20 32 40
速度(千米/时) 100 80
(1)行驶的时间和速度成什么比例关系?说明理由。
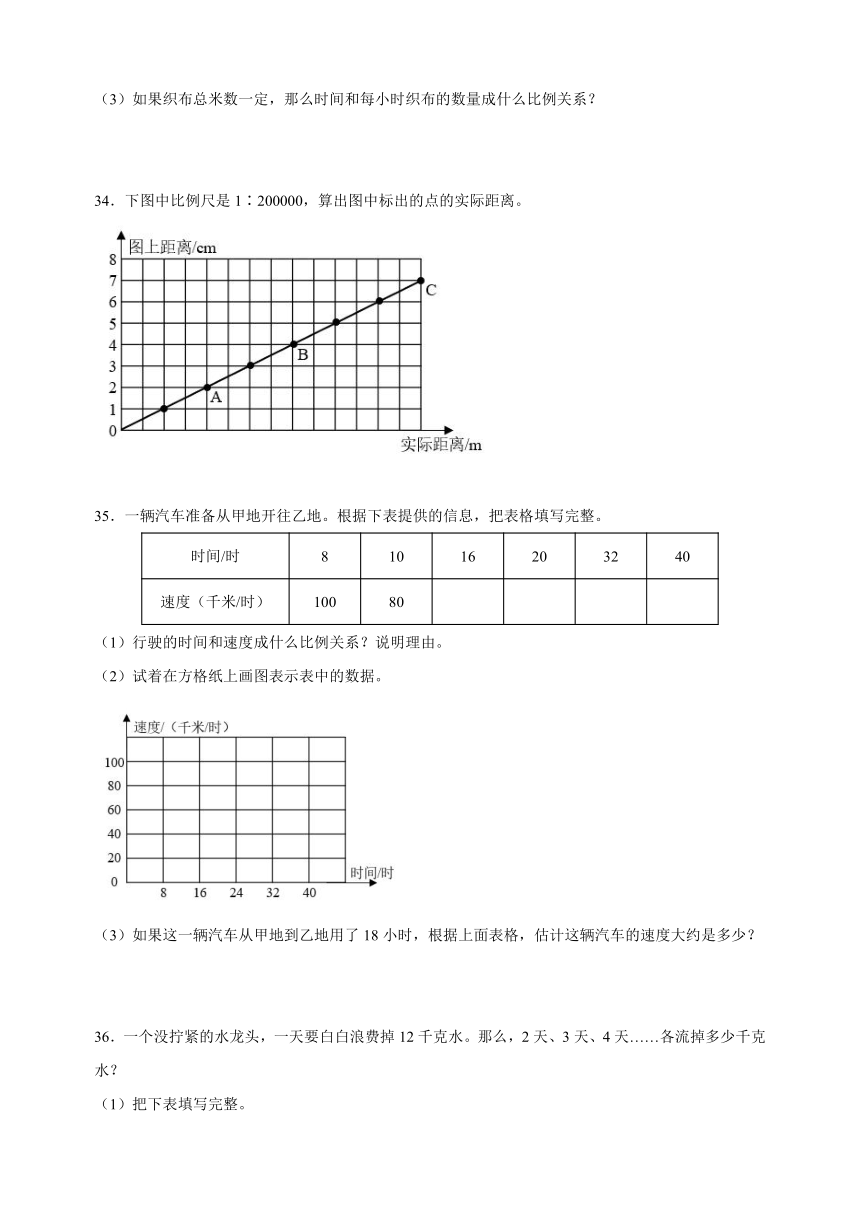
(2)试着在方格纸上画图表示表中的数据。
(3)如果这一辆汽车从甲地到乙地用了18小时,根据上面表格,估计这辆汽车的速度大约是多少?
36.一个没拧紧的水龙头,一天要白白浪费掉12千克水。那么,2天、3天、4天……各流掉多少千克水?
(1)把下表填写完整。
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 …
(2)根据表中的数量,在下图中描出天数和流掉的水量的对应点,再把它们按顺序连起来。
(3)水龙头流水的天数和流掉的水量成正比例吗?你是根据什么判断的?
(4)3.5天大约流掉多少千克的水?
参考答案
一、填空。(每空1分,共16分)
1、正 正
【解析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】路程÷时间=速度(比值一定),路程和速度成正比例。
路程和时间是两种相关联的量,当它们的比值(速度)保持一定时,路程和时间是成正比例的量,它们的关系是正比例关系。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
2、正
【解析】判断面粉的总质量和袋数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为面粉的总质量÷面粉的袋数=每袋面粉的质量(一定),符合正比例的意义,所以每袋面粉的质量一定,面粉的总质量和袋数成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3、反
【解析】总价=单价×数量,总价一定,故单价和数量成反比例.
4、反比例
【解析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】速度和时间是两种相关联的量,它们与路程有下面的关系:
速度×时间=路程(一定);
已知路程一定,也就是速度与时间的乘积一定,所以速度与时间成反比例。
【点睛】此题重点考查正比例和反比例的意义。
5、反
【解析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】因为每行站的人数和站的行数的乘积是总人数,总人数一定,所以每行站的人数和站的行数成反比例。
总人数一定,每行站的人数与站的行数成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
6、正
【解析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,否则就不成比例,据此解答即可。
【详解】耕地的公顷数÷耕地的天数=每天耕地的公顷数(一定),则耕地的天数和耕地的公顷数成正比例。
【点睛】此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
7、直线
【解析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图像是一条过原点的直径,据此解答。
【详解】根据分析可知,正比例图形是一条直线。
如图:
总价与数量成正比例,图像是一条直线。
【点睛】本题考查正比例意义以及图像的特征。
8.(1)成反比例(2)成反比例(3)不成比例(4)成正比例(5)不成比例(6)不成比例
【解析】
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此可以判断以下几题:
(1)因为:底面积×高=长方体体积(一定),底面积与高成反比例;
(2)根据三角形的底×高=三角形的面积×2,结合面积一定即可判断它的底和高成反比例;
(3)方砖面积×方砖块数=铺地的总面积(一定),可以看出,每块方砖的面积与方砖块数成反比例关系,而每块方砖的面积等于边长的平方,也就是说,铺地的方砖的面积一定时方砖的块数只是与方砖边长的平方成比例关系,与边长不成比例;
(4)圆的周长C=2πr,圆周率一定,周长和它的半径成正比例;
(5)圆的面积÷它的半径=π×它的半径,因为它的半径是变量,所以(π×它的半径)就不一定,是比值不一定,所以圆的面积与它的半径不成比例;
(6)已修长度+未修长度=公路的总长度(一定),和一定,所以已修长度和未修长度不成比例;
【小问1详解】长方体的体积一定,它的底面积和高。(成反比例)
【小问2详解】三角形的面积一定,它的底和高。(成反比例)
【小问3详解】铺地的面积一定,所用方砖的边长和所需块数。(不成比例)
【小问4详解】圆的周长和它的半径。(成正比例)
【小问5详解】圆的面积和它的半径。(不成比例)
【小问6详解】修一条公路,已修好的长度与未修好的长度。(不成比例)
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
9、①.正 ②.正
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】路程÷时间=速度(一定),路程和时间成正比例;
路程÷速度=时间(一定),速度和路程成正比例。
当速度一定时,路程是时间成正比例;当时间一定时,速度和路程成正比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
二、我当小法官。(对的在括号里画“√”,错的画“×”)(每小题1分,共10分)
10、×
【解析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定;如果是比值一定,就成正比例;据此进行解答即可。
【详解】气温与月份两个量对应比值不一定,所以气温与月份不成正比例。
原题干说法错误。故答案为:×
【点睛】熟练掌握正比例意义和辨识是解答本题的关键。
11、√
【解析】根据倒数的定义:乘积为1的两个数,互为倒数。两数之积一定,根据反比例的判别原则:当一个量一定,另两个量积一定时,成反比例,即可解答。
【详解】任何一个非0自然数,与它的倒数成反比例。所以原题说法正确。
【点睛】此题考查学生对反比例的判别方法。
12、×
【解析】根据比中各部分之间的关系判断出:比的后项与比值的商一定还是乘积一定,如果是商一定就成正比例,如果是积一定就成反比例,否则不成比例;据此解答。
【详解】比值×后项=前项,前项一定,即比值与后项的积一定,二者成反比例,所以原题说法错误。
故答案为:×
【点睛】本题考查了正、反比例的意义,关键是要理解两个相关联的量,如果它们对应的数的比值一定,则这两个量成正比例;如果它们的乘积一定,则它们成反比例。
13、×
【解析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定;如果是比值一定,就成正比例;据此进行解答即可。
【详解】根据分析可知,两种相关联的量,如果相对应的两个数的比值一定,这两种量成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识是解答本题的关键。
14、√
【解析】因为行驶的路程和转的周数是两种相关联的量,车轮的直径一定,也就是车轮的周长一定,转动周数越多,路程就越长;即所行路程与车轮转动的周数的比值一定。
【详解】由分析可知;车轮的直径一定,所行路程与车轮转的周数成正比例,此说法正确。故答案为:√
【点睛】此题考查对正比例概念的理解以及判别方法的掌握。
15、×
【解析】略
16、√
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】每小时加工的个数×加工时间=零件总数(一定),每小时加工的个数和加工时间成反比例。
原题干说法正确。故答案为:√
【点睛】本题考查正比例意义和辨识、反比例意义和辨识;熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
17、√
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此进行解答即可。
【详解】工作总量=工作效率×工作时间,工作总量一定,即工作效率和工作时间乘积一定,工作时间和工作效率成反比例。原题干说法正确。故答案为:√
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
18、×
【解析】判断圆周率和半径是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。
【详解】因为圆的周长一定,圆的半径就一定,不存在两个变量的问题,所以圆周率和半径不成反比例;原题说法错误。故答案为:×。
【点睛】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断。
19、√
【解析】根据x÷y=k(一定),x、y、k≠0,x和y成正比例关系,进行分析。
【详解】长方形的面积÷长=宽(一定),长方形的宽一定,它的面积和长成正比例,说法正确。
故答案为:√
【点睛】关键是理解正比例的意义,商一定是正比例关系。
三、精挑细选。(把正确答案的序号填在括号里)(每小题2分,共20分)
20、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此逐项分析,进行解答。
【详解】A.长方形面积=长×宽;长方形面积一定,乘积一定,长和宽成反比例;
B.一个人的年龄和头发长度既不是比值一定,也不是乘积一定,所以一个人的年龄和头发长度不成比例;
C.路程÷速度=时间(一定),比值一定,路程和速度成正比例;
D.全班人数-女生人数=男生人数(一定),和一定,所以女生人数和全班人数不成比例。故答案为:C
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
21、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】爸爸和儿子两人的年龄是两个变量,虽然年龄差不变,但是两个变量的比值和乘积都不一定,所以爸爸和儿子两人的年龄不成比例;故选:C。
【点睛】本题考查了辨识成正、反比例的量,关键是要理解辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5x=y,所以y∶x=5(一定)是比值一定,所以x和y成正比例;故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
23、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a∶b=4∶5(比值一定),所以a和b成正比例。故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
24、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】因为y=kx,所以=k(一定),x与y成正比例。
三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量成正比例。故答案为:A
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
25、B
【解析】根据反比例意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量的乘积一定,那么这两个量叫做反比例的量,它们的关系叫做反比例关系,据此逐项分析,进行解答。
【详解】A.x+y=100(和一定),x和y不成比例,不符合题意;
B.xy=35(积一定),x和y成反比例,符合题意;
C.=8(比值一定),x和y成正比例,不符合题意。
表示x和y成反比例的式子是xy=35。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
26、B
【解析】判断每箱苹果的质量和箱数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】每箱苹果的质量×箱数=苹果的总质量(一定),每箱苹果的质量和箱数成反比例。
苹果的总质量一定,每箱苹果的质量和箱数成反比例。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
27、B
【解析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。故答案为:B
28、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】加工零件总数÷加工时间=每小时加工零件个数,每小时加工20个零件(比值一定),加工零件的总数与加工时间成正比例。
每小时加工20个零件,加工零件的总数与加工时间成正比例。故答案为:A
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
29、B
【解析】判断x和y成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因为xy=k+,当k一定时,那么k+也一定,x和y是乘积一定,所以x和y成反比例。
已知xy=k+,k一定时,x和y成反比例。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
30.(1)①时间 ②路程
(2)①扩大 ②缩小 ③一定 ④速度
(3)正
【解析】
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【小问1详解】表中相关联的两种量是时间和路程。
【小问2详解】时间扩大时,路程也扩大;时间缩小时,路程也缩小。它们扩大或缩小的规律是:路程和时间相对应的两个量的比值一定,也就是速度一定。
【小问3详解】在路程、时间、速度三者之间存在着=速度(一定)的数量关系,这就是说速度一定,路程与时间成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
31. x=36;x=40;x=39.2 x=3;x=6;x
【解析】
(1)根据比例的基本性质,把原式化为2.5x=7.5×12,然后等式的两边同时除以2.5;
(2)根据比例的基本性质,把比例化为方程x=15×,两边再同时乘6。
(3)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以4求解;
(4)依据等式的性质,方程两边同时减2.25,再同时除以3求解;
(5)根据比例的基本性质,把比例化为方程0.7 x=3.5×1.2,两边再同时除以0.7。
(6)根据比例的基本性质,把比例化为方程x=×,两边再同时乘5。
【详解】(1)7.5∶x=2.5∶12
解:2.5x=7.5×12
2.5x=90
x=90÷2.5
x=36
(2)∶=x∶15
解:x=15×
x=
x=÷
x=×6
x=40
(3)
解:
4x=22.4×7
4x=156.8
x=156.8÷4
x=39.2
(4)2.25+3x=
解:3x=-2.25
3x=11.25-2.25
3x=9
x=9÷3
x=3
(5)3.5∶x=0.7∶1.2
解:0.7x=3.5×1.2
0.7x=4.2
x=4.2÷0.7
x=6
(6)∶x∶
解:x=×
x=
x=÷
x=×5
x=
32.(1)①.16 ②.24 ③.14 ④.28 ⑤.448
(2)①.4 ②.2 ③.1 ④.224 ⑤.112
【解析】
【分析】依据正比例的定义:两个相关联的量,如果它们的比值是一个定值,它们就成正比例。依据反比例的定义:两个相关联的量,如果它们的各是一个定值,它们就成反比例。
【小问1详解】已知表中的x与y成正比例关系,请完成下表。
x 2 4 8 ( 16 ) ( 24 ) 64
y ( 14 ) ( 28 ) 56 112 168 ( 448 )
【小问2详解】已知表中的x与y成反比例关系,请完成下表。
x 2 4 8 ( 4 ) ( 2 ) ( 1 )
y ( 224 ) ( 112 ) 56 112 224 448
【点睛】此题考查了正、反比例的意义,根据正、反比例的意义以及比例的基本性质来计算求解。
七、解决问题。(共25分)
33.(1)织布米数随时间的增长而增长 (2)正比例 (3)反比例
【解析】
【分析】(1)根据时间和织布的米数之间的关系,确定出两种量的变化规律;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(3)根据正、反比例的辨识,如果织布总米数一定,每小时织布的数量×时间=织布总米数(一定),判断时间和每小时织布的数量成什么比例,据此解答。
【详解】(1)织布米数=每小时织布米数×时间
1×15=30(米);2×15=30(米);3×15=45(米)……9×15=135(米);织布的米数随着时间的增长而增长。
答:织布的米数随时间的增长而增长。
(2)1÷15=2÷30=3÷45=4÷60=5÷75=6÷90=7÷105=8÷120=9÷135=(一定),织布时间和织布米数成正比例。
答:织布时间和织布米数两种量成正比例。
(3)每小时织布米数×时间=织布总米数(一定),时间和每小时织布米数成反比例。
答:如果织布总米数一定,那么时间和每小时织布的数量成反比例。
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
34.A:4000米,B:8000米,C:14000米
【解析】
【分析】横轴表示实际距离,竖轴表示图上距离,算出各个点的图上距离,再根据实际距离=图上距离÷比例尺,解答此题即可。
【详解】A点图上距离为2格,因此是2÷=400000(厘米)=4000米
B点图上距离为4格,因此是4÷=800000(厘米)=8000米
C点图上距离为7格,因此是7÷=1400000(厘米)=14000米
答:A点实际距离为4000米,B点实际距离为8000米,C点实际距离为14000米。
【点睛】本题主要考查了比例尺的知识应用。
35.(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)见详解;
(3)44千米。
【解析】
(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)根据路程、时间、速度三者之间的关系,求出对应的速度,填写表格。
(3)因为18小时介于16小时与20小时之间,那么速度就介于50与40之间,估算即可;
【详解】补充表格如下:
时间(时) 8 10 16 20 32 40
速度(千米/时) 100 80 50 40 25 20
(1)因为8×100=800(千米),10×80=800(千米),即路程一定,时间与速度成反比例;
(2)画图表示表中的数据:
(3)800÷18≈44(千米)
答:这辆汽车的速度大约是每小时44千米。
【点睛】运用表中给出的数据,结合路程、时间、速度三者之间的关系,解决问题。
36.(1)见详解 (2)见详解 (3)成正比例,利用见详解 (4)42千克
【解析】
(1)利用天数乘每天白白流掉的水的质量即可;
(2)根据统计表中的数据,绘制成统计图;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(4)用每天流掉的水的质量×3.5天,即可解答。
【详解】(1)2×12=24(千克)
3×12=36(千克)
4×12=48(千克)
5×12=60(千克)
6×12=72(千克)
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 24 36 48 60 72 …
(2)图如下:
(3)1÷12=2÷24=3÷36=4÷48=5÷60=6÷72=(一定),水龙头流水的天数和流掉的水量成正比例。
(4)12×3.5=42(千克)
答:3.5天大约流掉42千克的水。
【点睛】解答本题先根据问题从图中找出所需的信息。然后根据数量关系式“天数×每天的流水量=总流水量”即可作出解答。
第六单元《正比例和反比例》
姓名:_________ 班级:_________ 学号:_________
(时间:60分钟 分值:100分)
一、填空。(每空1分,共16分)
1.路程和时间是两种相关联的量,当它们的比值(速度)保持一定时,路程和时间是成( )比例的量,它们的关系是( )比例关系。
2.每袋面粉的质量一定,面粉的总质量和袋数成( )比例。
3.总价一定,单价和数量成( )比例.
4.路程一定,速度和时间成( )。
5.总人数一定,每行站的人数与站的行数成( )比例。
6.每天耕地的公顷数一定,耕地的天数和耕地的公顷数成( )比例。
7.正比例的图像是一条( )。
8.判断下面各题中的两种量是否成比例,如果成比例,成什么比例。
(1)长方体的体积一定,它的底面积和高。( )
(2)三角形的面积一定,它的底和高。( )
(3)铺地的面积一定,所用方砖的边长和所需块数。( )
(4)圆的周长和它的半径。( )
(5)圆的面积和它的半径。( )
(6)修一条公路,已修好的长度与未修好的长度。( )
9.当速度一定时,路程与时间成( )比例;当时间一定时,速度与路程成( )比例。
二、判断题。(对的在括号里画“√”,错的画“×”)(每小题1分,共10分)
10.气温与月份成正比例。( )
11.任何一个非0自然数,与它的倒数成反比例。( )
12.比的前项一定,比的后项和比值成正比例。( )
13.两种相关联的量,如果相对应的两个数一定,这两种量成正比例。( )
14.车轮的直径一定,所行路程与车轮转的周数成正比例。( )
15.一本书的总页数一定,已读的页数和未读的页数成反比例。( )
16.零件总数一定,每小时加工的个数和加工时间成反比例。( )
17.工作总量一定,工作时间和工作效率成反比例。( )
18.圆的周长一定,圆周率和半径成反比例。______
19.长方形的宽一定,它的面积和长成正比例。( )
三、精挑细选。(把正确答案的序号填在括号里)(每小题2分,共20分)
20.下面每组的两个量中,成正比例关系的是( )。
A.长方形的面积一定,长和宽 B.一个人的年龄和头发长度
C.时间一定,路程和速度 D.男生人数一定,女生人数和全班人数
21.爸爸和儿子两人的年龄( )。
A.成正比例 B.成反比例 C.不成比例
22.如果5x=y,那么x和y( )。
A.成正比例 B.成反比例 C.不成比例
23.已知a∶b=4∶5,那么a和b( )。
A.不成比例 B.成反比例 C.成正比例
24.三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量( )。
A.成正比例 B.成反比例 C.不成比例
25.表示x和y成反比例的式子是( )。
A.x+y=100 B.xy=35 C.x/y=8
26.苹果的总质量一定,每箱苹果的质量和箱数( )。
A.成正比例 B.成反比例 C.不成比例
27.圆柱的体积一定,底面积和高( )
A.成正比例 B.成反比例 C.不成比例
28.每小时加工20个零件,加工零件的总数与加工时间( )。
A.成正比例 B.成反比例 C.不成比例
29.已知xy=k+,k一定时,x和y( )。
A.成正比例 B.成反比例 C.不成比例
30.一辆汽车行驶的时间和所行的路程如下表,看表填空。
时间/时 1 2 3 4 5 6 7 8 9 …
路程/千米 50 100 150 200 250 300 350 400 450 …
(1)表中相关联的两种量是( )和( )。
(2)时间扩大时,路程也( );时间缩小时,路程也( )。它们扩大或缩小规律是:路程和时间相对应的两个量的比值( ),也就是( )一定。
(3)在路程、时间、速度三者之间存在着=速度(一定)数量关系,这就是说速度一定,路程与时间成( )比例。
31.解比例。
7.5∶x=2.5∶12 ∶=x∶15
2.25+3x= 3.5∶x=0.7∶1.2 ∶x∶
32.根据正比例或反比例的关系填写下表。
(1)已知表中的x与y成正比例关系,请完成下表。
x 2 4 8 ( ) ( ) 64
y ( ) ( ) 56 112 168 ( )
(2)已知表中的x与y成反比例关系,请完成下表。
x 2 4 8 ( ) ( ) ( )
y ( ) ( ) 56 112 224 448
七、解决问题。(共25分)
33.一台织布机织布的时间和织布的米数如下表:
时间/时 1 2 3 4 5 6 7 8 9 …
织布的米数/米 15 30 45 60 75 90 105 120 135 …
(1)上表中的两种量的变化有什么规律?
(2)上表中两种量成什么比例关系?
(3)如果织布总米数一定,那么时间和每小时织布的数量成什么比例关系?
34.下图中比例尺是1∶200000,算出图中标出的点的实际距离。
35.一辆汽车准备从甲地开往乙地。根据下表提供的信息,把表格填写完整。
时间/时 8 10 16 20 32 40
速度(千米/时) 100 80
(1)行驶的时间和速度成什么比例关系?说明理由。
(2)试着在方格纸上画图表示表中的数据。
(3)如果这一辆汽车从甲地到乙地用了18小时,根据上面表格,估计这辆汽车的速度大约是多少?
36.一个没拧紧的水龙头,一天要白白浪费掉12千克水。那么,2天、3天、4天……各流掉多少千克水?
(1)把下表填写完整。
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 …
(2)根据表中的数量,在下图中描出天数和流掉的水量的对应点,再把它们按顺序连起来。
(3)水龙头流水的天数和流掉的水量成正比例吗?你是根据什么判断的?
(4)3.5天大约流掉多少千克的水?
参考答案
一、填空。(每空1分,共16分)
1、正 正
【解析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】路程÷时间=速度(比值一定),路程和速度成正比例。
路程和时间是两种相关联的量,当它们的比值(速度)保持一定时,路程和时间是成正比例的量,它们的关系是正比例关系。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
2、正
【解析】判断面粉的总质量和袋数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为面粉的总质量÷面粉的袋数=每袋面粉的质量(一定),符合正比例的意义,所以每袋面粉的质量一定,面粉的总质量和袋数成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
3、反
【解析】总价=单价×数量,总价一定,故单价和数量成反比例.
4、反比例
【解析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系。
【详解】速度和时间是两种相关联的量,它们与路程有下面的关系:
速度×时间=路程(一定);
已知路程一定,也就是速度与时间的乘积一定,所以速度与时间成反比例。
【点睛】此题重点考查正比例和反比例的意义。
5、反
【解析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
【详解】因为每行站的人数和站的行数的乘积是总人数,总人数一定,所以每行站的人数和站的行数成反比例。
总人数一定,每行站的人数与站的行数成反比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
6、正
【解析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,否则就不成比例,据此解答即可。
【详解】耕地的公顷数÷耕地的天数=每天耕地的公顷数(一定),则耕地的天数和耕地的公顷数成正比例。
【点睛】此题属于根据正、反比例的意义,判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断。
7、直线
【解析】两种相关联的量中相对应的两个数的商一定,就成正比例关系,正比例的图像是一条过原点的直径,据此解答。
【详解】根据分析可知,正比例图形是一条直线。
如图:
总价与数量成正比例,图像是一条直线。
【点睛】本题考查正比例意义以及图像的特征。
8.(1)成反比例(2)成反比例(3)不成比例(4)成正比例(5)不成比例(6)不成比例
【解析】
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此可以判断以下几题:
(1)因为:底面积×高=长方体体积(一定),底面积与高成反比例;
(2)根据三角形的底×高=三角形的面积×2,结合面积一定即可判断它的底和高成反比例;
(3)方砖面积×方砖块数=铺地的总面积(一定),可以看出,每块方砖的面积与方砖块数成反比例关系,而每块方砖的面积等于边长的平方,也就是说,铺地的方砖的面积一定时方砖的块数只是与方砖边长的平方成比例关系,与边长不成比例;
(4)圆的周长C=2πr,圆周率一定,周长和它的半径成正比例;
(5)圆的面积÷它的半径=π×它的半径,因为它的半径是变量,所以(π×它的半径)就不一定,是比值不一定,所以圆的面积与它的半径不成比例;
(6)已修长度+未修长度=公路的总长度(一定),和一定,所以已修长度和未修长度不成比例;
【小问1详解】长方体的体积一定,它的底面积和高。(成反比例)
【小问2详解】三角形的面积一定,它的底和高。(成反比例)
【小问3详解】铺地的面积一定,所用方砖的边长和所需块数。(不成比例)
【小问4详解】圆的周长和它的半径。(成正比例)
【小问5详解】圆的面积和它的半径。(不成比例)
【小问6详解】修一条公路,已修好的长度与未修好的长度。(不成比例)
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
9、①.正 ②.正
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】路程÷时间=速度(一定),路程和时间成正比例;
路程÷速度=时间(一定),速度和路程成正比例。
当速度一定时,路程是时间成正比例;当时间一定时,速度和路程成正比例。
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
二、我当小法官。(对的在括号里画“√”,错的画“×”)(每小题1分,共10分)
10、×
【解析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定;如果是比值一定,就成正比例;据此进行解答即可。
【详解】气温与月份两个量对应比值不一定,所以气温与月份不成正比例。
原题干说法错误。故答案为:×
【点睛】熟练掌握正比例意义和辨识是解答本题的关键。
11、√
【解析】根据倒数的定义:乘积为1的两个数,互为倒数。两数之积一定,根据反比例的判别原则:当一个量一定,另两个量积一定时,成反比例,即可解答。
【详解】任何一个非0自然数,与它的倒数成反比例。所以原题说法正确。
【点睛】此题考查学生对反比例的判别方法。
12、×
【解析】根据比中各部分之间的关系判断出:比的后项与比值的商一定还是乘积一定,如果是商一定就成正比例,如果是积一定就成反比例,否则不成比例;据此解答。
【详解】比值×后项=前项,前项一定,即比值与后项的积一定,二者成反比例,所以原题说法错误。
故答案为:×
【点睛】本题考查了正、反比例的意义,关键是要理解两个相关联的量,如果它们对应的数的比值一定,则这两个量成正比例;如果它们的乘积一定,则它们成反比例。
13、×
【解析】判断两个相关联的量之间成正比例,就看这两个量是对应的比值一定;如果是比值一定,就成正比例;据此进行解答即可。
【详解】根据分析可知,两种相关联的量,如果相对应的两个数的比值一定,这两种量成正比例。
原题干说法错误。
故答案为:×
【点睛】熟练掌握正比例意义和辨识是解答本题的关键。
14、√
【解析】因为行驶的路程和转的周数是两种相关联的量,车轮的直径一定,也就是车轮的周长一定,转动周数越多,路程就越长;即所行路程与车轮转动的周数的比值一定。
【详解】由分析可知;车轮的直径一定,所行路程与车轮转的周数成正比例,此说法正确。故答案为:√
【点睛】此题考查对正比例概念的理解以及判别方法的掌握。
15、×
【解析】略
16、√
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】每小时加工的个数×加工时间=零件总数(一定),每小时加工的个数和加工时间成反比例。
原题干说法正确。故答案为:√
【点睛】本题考查正比例意义和辨识、反比例意义和辨识;熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
17、√
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此进行解答即可。
【详解】工作总量=工作效率×工作时间,工作总量一定,即工作效率和工作时间乘积一定,工作时间和工作效率成反比例。原题干说法正确。故答案为:√
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
18、×
【解析】判断圆周率和半径是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例。
【详解】因为圆的周长一定,圆的半径就一定,不存在两个变量的问题,所以圆周率和半径不成反比例;原题说法错误。故答案为:×。
【点睛】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断。
19、√
【解析】根据x÷y=k(一定),x、y、k≠0,x和y成正比例关系,进行分析。
【详解】长方形的面积÷长=宽(一定),长方形的宽一定,它的面积和长成正比例,说法正确。
故答案为:√
【点睛】关键是理解正比例的意义,商一定是正比例关系。
三、精挑细选。(把正确答案的序号填在括号里)(每小题2分,共20分)
20、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此逐项分析,进行解答。
【详解】A.长方形面积=长×宽;长方形面积一定,乘积一定,长和宽成反比例;
B.一个人的年龄和头发长度既不是比值一定,也不是乘积一定,所以一个人的年龄和头发长度不成比例;
C.路程÷速度=时间(一定),比值一定,路程和速度成正比例;
D.全班人数-女生人数=男生人数(一定),和一定,所以女生人数和全班人数不成比例。故答案为:C
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
21、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】爸爸和儿子两人的年龄是两个变量,虽然年龄差不变,但是两个变量的比值和乘积都不一定,所以爸爸和儿子两人的年龄不成比例;故选:C。
【点睛】本题考查了辨识成正、反比例的量,关键是要理解辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
22、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为5x=y,所以y∶x=5(一定)是比值一定,所以x和y成正比例;故答案为:A
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
23、C
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】因为a∶b=4∶5(比值一定),所以a和b成正比例。故答案为:C
【点睛】此题属于根据正、反比例的意义,辨识两种相关联的量是否成反比例,就看这两种量是否是对应的乘积一定,再做出选择。
24、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】因为y=kx,所以=k(一定),x与y成正比例。
三个量x、y、k(k≠0)的关系是y=kx,当k一定时,x与y这两个量成正比例。故答案为:A
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
25、B
【解析】根据反比例意义:两个相关联的量,一个量变化,另一个量也随着变化,如果相对应的两个量的乘积一定,那么这两个量叫做反比例的量,它们的关系叫做反比例关系,据此逐项分析,进行解答。
【详解】A.x+y=100(和一定),x和y不成比例,不符合题意;
B.xy=35(积一定),x和y成反比例,符合题意;
C.=8(比值一定),x和y成正比例,不符合题意。
表示x和y成反比例的式子是xy=35。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
26、B
【解析】判断每箱苹果的质量和箱数之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【详解】每箱苹果的质量×箱数=苹果的总质量(一定),每箱苹果的质量和箱数成反比例。
苹果的总质量一定,每箱苹果的质量和箱数成反比例。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
27、B
【解析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例。故答案为:B
28、A
【解析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
【详解】加工零件总数÷加工时间=每小时加工零件个数,每小时加工20个零件(比值一定),加工零件的总数与加工时间成正比例。
每小时加工20个零件,加工零件的总数与加工时间成正比例。故答案为:A
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
29、B
【解析】判断x和y成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【详解】因为xy=k+,当k一定时,那么k+也一定,x和y是乘积一定,所以x和y成反比例。
已知xy=k+,k一定时,x和y成反比例。故答案为:B
【点睛】熟练掌握正比例意义和辨识、反比例意义和辨识是解答本题的关键。
30.(1)①时间 ②路程
(2)①扩大 ②缩小 ③一定 ④速度
(3)正
【解析】
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【小问1详解】表中相关联的两种量是时间和路程。
【小问2详解】时间扩大时,路程也扩大;时间缩小时,路程也缩小。它们扩大或缩小的规律是:路程和时间相对应的两个量的比值一定,也就是速度一定。
【小问3详解】在路程、时间、速度三者之间存在着=速度(一定)的数量关系,这就是说速度一定,路程与时间成正比例。
【点睛】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
31. x=36;x=40;x=39.2 x=3;x=6;x
【解析】
(1)根据比例的基本性质,把原式化为2.5x=7.5×12,然后等式的两边同时除以2.5;
(2)根据比例的基本性质,把比例化为方程x=15×,两边再同时乘6。
(3)先根据比例基本性质:两内项之积等于两外项之积,化简方程,再依据等式的性质,方程两边同时除以4求解;
(4)依据等式的性质,方程两边同时减2.25,再同时除以3求解;
(5)根据比例的基本性质,把比例化为方程0.7 x=3.5×1.2,两边再同时除以0.7。
(6)根据比例的基本性质,把比例化为方程x=×,两边再同时乘5。
【详解】(1)7.5∶x=2.5∶12
解:2.5x=7.5×12
2.5x=90
x=90÷2.5
x=36
(2)∶=x∶15
解:x=15×
x=
x=÷
x=×6
x=40
(3)
解:
4x=22.4×7
4x=156.8
x=156.8÷4
x=39.2
(4)2.25+3x=
解:3x=-2.25
3x=11.25-2.25
3x=9
x=9÷3
x=3
(5)3.5∶x=0.7∶1.2
解:0.7x=3.5×1.2
0.7x=4.2
x=4.2÷0.7
x=6
(6)∶x∶
解:x=×
x=
x=÷
x=×5
x=
32.(1)①.16 ②.24 ③.14 ④.28 ⑤.448
(2)①.4 ②.2 ③.1 ④.224 ⑤.112
【解析】
【分析】依据正比例的定义:两个相关联的量,如果它们的比值是一个定值,它们就成正比例。依据反比例的定义:两个相关联的量,如果它们的各是一个定值,它们就成反比例。
【小问1详解】已知表中的x与y成正比例关系,请完成下表。
x 2 4 8 ( 16 ) ( 24 ) 64
y ( 14 ) ( 28 ) 56 112 168 ( 448 )
【小问2详解】已知表中的x与y成反比例关系,请完成下表。
x 2 4 8 ( 4 ) ( 2 ) ( 1 )
y ( 224 ) ( 112 ) 56 112 224 448
【点睛】此题考查了正、反比例的意义,根据正、反比例的意义以及比例的基本性质来计算求解。
七、解决问题。(共25分)
33.(1)织布米数随时间的增长而增长 (2)正比例 (3)反比例
【解析】
【分析】(1)根据时间和织布的米数之间的关系,确定出两种量的变化规律;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(3)根据正、反比例的辨识,如果织布总米数一定,每小时织布的数量×时间=织布总米数(一定),判断时间和每小时织布的数量成什么比例,据此解答。
【详解】(1)织布米数=每小时织布米数×时间
1×15=30(米);2×15=30(米);3×15=45(米)……9×15=135(米);织布的米数随着时间的增长而增长。
答:织布的米数随时间的增长而增长。
(2)1÷15=2÷30=3÷45=4÷60=5÷75=6÷90=7÷105=8÷120=9÷135=(一定),织布时间和织布米数成正比例。
答:织布时间和织布米数两种量成正比例。
(3)每小时织布米数×时间=织布总米数(一定),时间和每小时织布米数成反比例。
答:如果织布总米数一定,那么时间和每小时织布的数量成反比例。
【点睛】熟练掌握正比例意义和辨识,反比例意义和辨识是解答本题的关键。
34.A:4000米,B:8000米,C:14000米
【解析】
【分析】横轴表示实际距离,竖轴表示图上距离,算出各个点的图上距离,再根据实际距离=图上距离÷比例尺,解答此题即可。
【详解】A点图上距离为2格,因此是2÷=400000(厘米)=4000米
B点图上距离为4格,因此是4÷=800000(厘米)=8000米
C点图上距离为7格,因此是7÷=1400000(厘米)=14000米
答:A点实际距离为4000米,B点实际距离为8000米,C点实际距离为14000米。
【点睛】本题主要考查了比例尺的知识应用。
35.(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)见详解;
(3)44千米。
【解析】
(1)因为路程一定,所以行驶的时间和速度成反比例关系;
(2)根据路程、时间、速度三者之间的关系,求出对应的速度,填写表格。
(3)因为18小时介于16小时与20小时之间,那么速度就介于50与40之间,估算即可;
【详解】补充表格如下:
时间(时) 8 10 16 20 32 40
速度(千米/时) 100 80 50 40 25 20
(1)因为8×100=800(千米),10×80=800(千米),即路程一定,时间与速度成反比例;
(2)画图表示表中的数据:
(3)800÷18≈44(千米)
答:这辆汽车的速度大约是每小时44千米。
【点睛】运用表中给出的数据,结合路程、时间、速度三者之间的关系,解决问题。
36.(1)见详解 (2)见详解 (3)成正比例,利用见详解 (4)42千克
【解析】
(1)利用天数乘每天白白流掉的水的质量即可;
(2)根据统计表中的数据,绘制成统计图;
(3)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;据此解答。
(4)用每天流掉的水的质量×3.5天,即可解答。
【详解】(1)2×12=24(千克)
3×12=36(千克)
4×12=48(千克)
5×12=60(千克)
6×12=72(千克)
天数/天 1 2 3 4 5 6 …
流掉的水量/千克 12 24 36 48 60 72 …
(2)图如下:
(3)1÷12=2÷24=3÷36=4÷48=5÷60=6÷72=(一定),水龙头流水的天数和流掉的水量成正比例。
(4)12×3.5=42(千克)
答:3.5天大约流掉42千克的水。
【点睛】解答本题先根据问题从图中找出所需的信息。然后根据数量关系式“天数×每天的流水量=总流水量”即可作出解答。
