数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共20张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册3.2.1双曲线及其标准方程 课件(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 18:42:38 | ||
图片预览





文档简介
(共20张PPT)
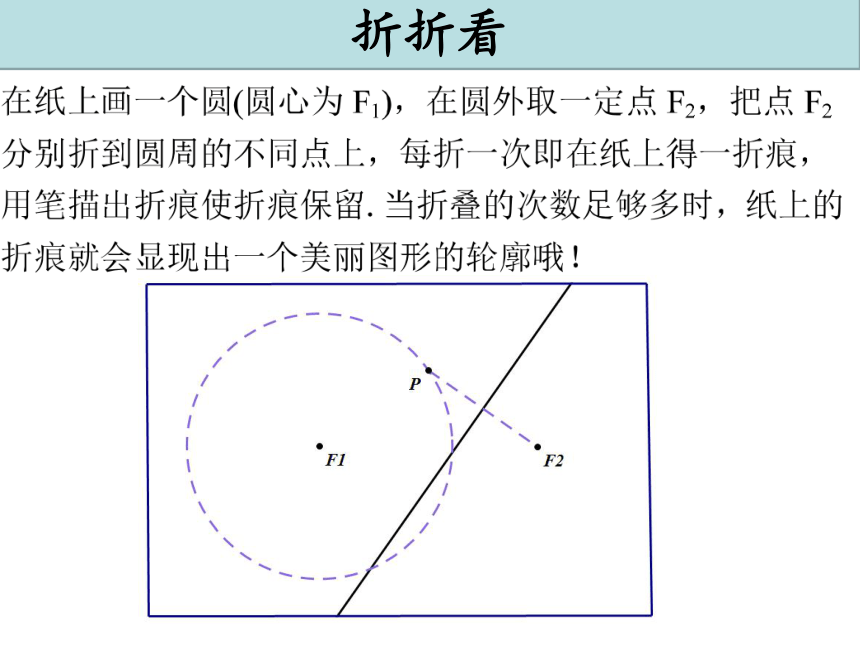
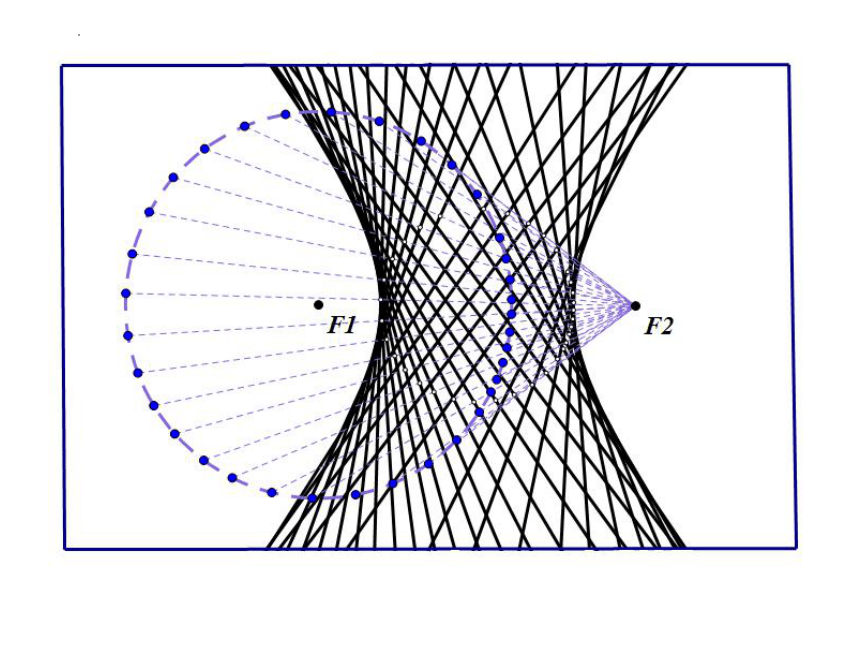
回忆童年的折纸游戏
折折看
双曲线
双曲线及其标准方程
欣赏:生活中的双曲线
德基水库是台湾第一座由混凝土为材料所构成的双曲线薄型拱坝,大坝高度为180公尺,长度为290公尺,顶部宽度为4.5公尺,为目前台湾最高之水坝。
德基水库
路思义教堂
路思义教堂是在建筑学上应用双曲线最有名的建筑之一。
工业冷却塔
清酒瓶
广州塔
双曲线在工程、光学、声学上都有很多应用,在土木工程中双曲线就被用来评估基桩极限承载力,以图解法取代复杂的数学运算。
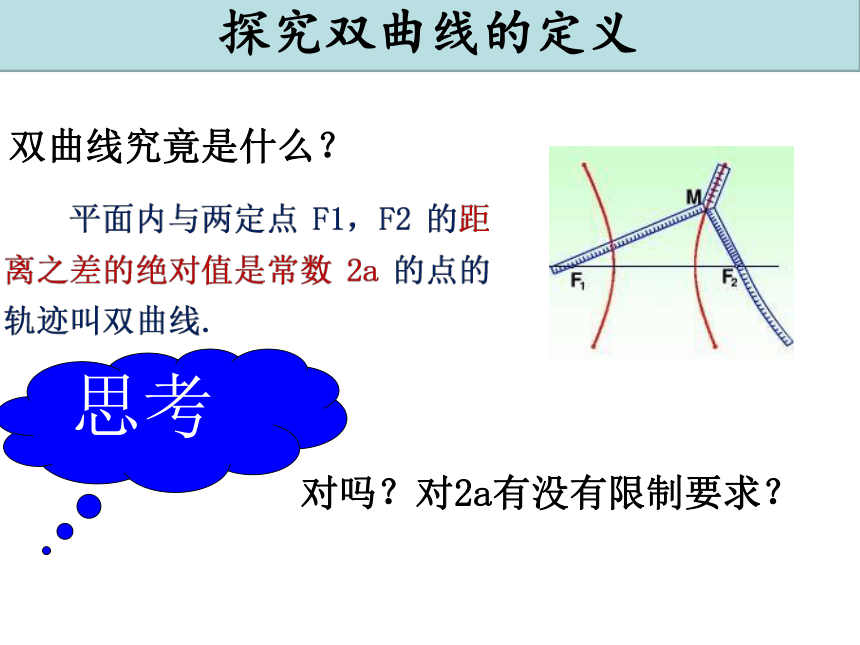
探究双曲线的定义
双曲线究竟是什么?
对吗?对2a有没有限制要求?
思考
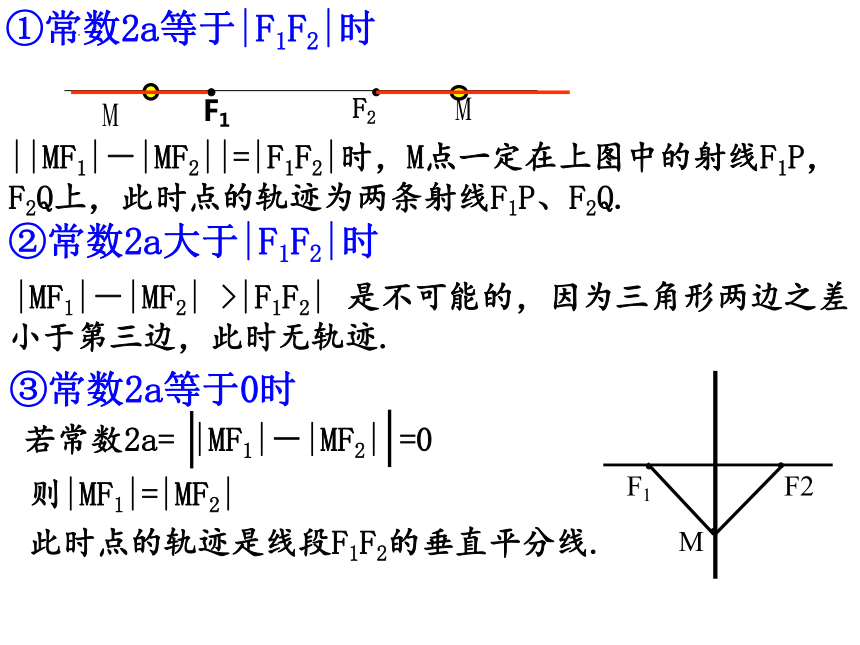
||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q上,此时点的轨迹为两条射线F1P、F2Q.
②常数2a大于|F1F2|时
①常数2a等于|F1F2|时
|MF1|-|MF2| >|F1F2|
F2
F1
M
M
是不可能的,因为三角形两边之差小于第三边,此时无轨迹.
此时点的轨迹是线段F1F2的垂直平分线.
则|MF1|=|MF2|
F1
F2
M
③常数2a等于0时
若常数2a= |MF1|-|MF2| =0
双曲线的定义
因此,在应用定义时,首先要考查
2a与 |F1F2| 的大小
思考:如何绘制精准的双曲线图像
既然双曲线在工程上有这么多的应用,那么工程师们在工程绘图的过程中就要画出精准的双曲线图像, 总不能通过折纸或拉拉链的方法来制图吧?怎么办?
研究双曲线的标准方程可使我们精确地确定双曲线上每点的位置.
定性
定量
x
y
o
1.如图建立坐标系,使x轴经过F1、F2, 并且原点O与线段F1F2的中点重合
2.设M(x,y)为双曲线上任一点,双曲线焦距为2c(c>0),则F1(-c,0), F2(c,0)
F1
F2
M
3.列式:P= {M ||MF1 | - | MF2| = + 2a }
_
cx -a2=±a (x-c)2+y2
4.化简:移项平方整理得:
再次平方得: (c2-a2) x2-a2y2=a2(c2-a2)
由双曲线的定义知,2c>2a,即c>a,故c2-a2>0,
令c2-a2=b2,其中b>0,代入整理得:
双曲线的标准方程
=
x2
a2
-
y2
b2
1
(a>0,b>0)
方程
叫做双曲线的标准方程
它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2
=
x2
a2
-
y2
b2
1
(a>0,b>0)
x2
y2
方程
叫做双曲线的标准方程
它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2
双曲线的标准方程
看 前的系数,哪一个为正,则在哪一个轴上
2、双曲线的标准方程与椭圆的标准方程有何区别与联系
1、如何判断双曲线的焦点在哪个轴上?
思考
焦点在x轴上
焦点在y轴上
定 义
方 程
焦 点
a.b.c的关系 F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
双曲线与椭圆之间的区别与联系
有兴趣的同学们课后可思考,这两个双曲线从图像上来看有什么联系 (提示:可预习双曲线的图像及性质)
所求轨迹的方程为:
已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.
两条射线
轨迹不存在
例题分析
x2与y2项分母的大小
x2与y2项系数的正负
c2=a2+b2
AB<0
填一填
小结
1.双曲线定义及标准方程
3.双曲线与椭圆之间的区别与联系
2.求双曲线标准方程(定位,定量)
回忆童年的折纸游戏
折折看
双曲线
双曲线及其标准方程
欣赏:生活中的双曲线
德基水库是台湾第一座由混凝土为材料所构成的双曲线薄型拱坝,大坝高度为180公尺,长度为290公尺,顶部宽度为4.5公尺,为目前台湾最高之水坝。
德基水库
路思义教堂
路思义教堂是在建筑学上应用双曲线最有名的建筑之一。
工业冷却塔
清酒瓶
广州塔
双曲线在工程、光学、声学上都有很多应用,在土木工程中双曲线就被用来评估基桩极限承载力,以图解法取代复杂的数学运算。
探究双曲线的定义
双曲线究竟是什么?
对吗?对2a有没有限制要求?
思考
||MF1|-|MF2||=|F1F2|时,M点一定在上图中的射线F1P,F2Q上,此时点的轨迹为两条射线F1P、F2Q.
②常数2a大于|F1F2|时
①常数2a等于|F1F2|时
|MF1|-|MF2| >|F1F2|
F2
F1
M
M
是不可能的,因为三角形两边之差小于第三边,此时无轨迹.
此时点的轨迹是线段F1F2的垂直平分线.
则|MF1|=|MF2|
F1
F2
M
③常数2a等于0时
若常数2a= |MF1|-|MF2| =0
双曲线的定义
因此,在应用定义时,首先要考查
2a与 |F1F2| 的大小
思考:如何绘制精准的双曲线图像
既然双曲线在工程上有这么多的应用,那么工程师们在工程绘图的过程中就要画出精准的双曲线图像, 总不能通过折纸或拉拉链的方法来制图吧?怎么办?
研究双曲线的标准方程可使我们精确地确定双曲线上每点的位置.
定性
定量
x
y
o
1.如图建立坐标系,使x轴经过F1、F2, 并且原点O与线段F1F2的中点重合
2.设M(x,y)为双曲线上任一点,双曲线焦距为2c(c>0),则F1(-c,0), F2(c,0)
F1
F2
M
3.列式:P= {M ||MF1 | - | MF2| = + 2a }
_
cx -a2=±a (x-c)2+y2
4.化简:移项平方整理得:
再次平方得: (c2-a2) x2-a2y2=a2(c2-a2)
由双曲线的定义知,2c>2a,即c>a,故c2-a2>0,
令c2-a2=b2,其中b>0,代入整理得:
双曲线的标准方程
=
x2
a2
-
y2
b2
1
(a>0,b>0)
方程
叫做双曲线的标准方程
它表示的双曲线焦点在x轴上,焦点为F1(-c,0),F2(c,0),且c2=a2+b2
=
x2
a2
-
y2
b2
1
(a>0,b>0)
x2
y2
方程
叫做双曲线的标准方程
它表示的双曲线焦点在y轴上,焦点为F1(0,-c),F2(0,c),且c2=a2+b2
双曲线的标准方程
看 前的系数,哪一个为正,则在哪一个轴上
2、双曲线的标准方程与椭圆的标准方程有何区别与联系
1、如何判断双曲线的焦点在哪个轴上?
思考
焦点在x轴上
焦点在y轴上
定 义
方 程
焦 点
a.b.c的关系 F(±c,0)
F(±c,0)
a>0,b>0,但a不一定大于b,c2=a2+b2
a>b>0,a2=b2+c2
||MF1|-|MF2||=2a
|MF1|+|MF2|=2a
椭 圆
双曲线
F(0,±c)
F(0,±c)
双曲线与椭圆之间的区别与联系
有兴趣的同学们课后可思考,这两个双曲线从图像上来看有什么联系 (提示:可预习双曲线的图像及性质)
所求轨迹的方程为:
已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.
两条射线
轨迹不存在
例题分析
x2与y2项分母的大小
x2与y2项系数的正负
c2=a2+b2
AB<0
填一填
小结
1.双曲线定义及标准方程
3.双曲线与椭圆之间的区别与联系
2.求双曲线标准方程(定位,定量)
