数学人教A版(2019)选择性必修第三册7.1.2全概率公式 课件(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册7.1.2全概率公式 课件(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 984.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 19:42:07 | ||
图片预览








文档简介
(共24张PPT)
7.1.2
全概率公式
学习目标
1.结合古典概型,会利用全概率公式计算概率.
2.了解贝叶斯公式.
3.核心素养:数学抽象、逻辑推理、数学运算.
一、复习导入
1.条件
2.概率的乘法公式:= =.
3.条件概率的性质:设>0,
(1)=1;
(2)如果B和C是两个互斥事件,则
+
(3)设和互为对立事件,则
二、新课讲授
问题1 如图,有三个箱子,分别编号为1,2,3,其中1号箱有1个红球和4个白球, 2号箱有2个红球和3个白球, 3号箱有3个红球,这些球除了颜色外完全相同.现先从三箱中任取一箱,再从中任意取出一球,求取得红球的概率.
分析:用表示事件“球取自第号箱”( =1,2,3), 表示事件“取得红球”,其中 , 互斥, 发生总是伴随着 , 之一同时发生,即= ∪,且两两互斥.
由互斥事件概率的加法公式可得:
= )+
再对求和中的每一项用乘法公式可得:
= )+
即= + =
设 是试验的样本空间, , ,…, 为样本空间的一组基事件,若
(1) ,其中
(2) ∪… ∪ = ,
则称 , ,…, 为样本空间的一个划分.
设 , ,…, 为样本空间 的一个划分,若)>0 ,则对任意一个事件有:
全概率公式
多因一果
(1) ,其中
(2) ∪… ∪ = .
对全概率公式的认识:
1、某一事件的发生可能有各种原因,如果是由原因互斥,构成一个完备事件)所引起,则发生的概率是发生概率的总和.
2、每一个原因都可能导致发生,故发生的概率是各种原因引起, 发生概率的总和即全概率公式.
3、全概率公式本质上是综合运用加法公式和乘法公式解决“多因一果”的概率问题.
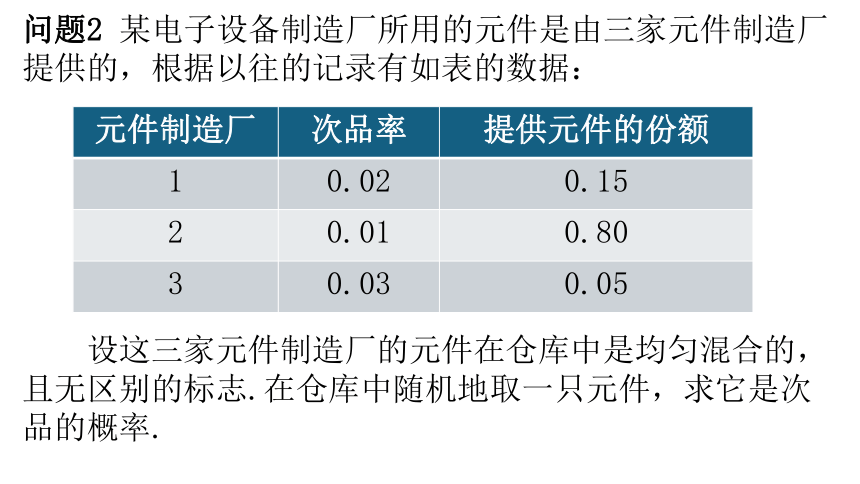
问题2 某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录有如表的数据:
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
分析:用表示事件“所取到的产品是由第家元件制造厂提供的”( =1,2,3), 表示事件“取到的是一件次品”,其中 , 互斥,发生总是伴随着 , 之一同时发生,即= ∪,且两两互斥.
则有:= )+
)+
=+
=
因此,在仓库中随机地取一只元件,它是次品的概率是.
运用全概率公式的一般步骤:
1、求出样本空间 的一个划分 , ,…, ;
2、求 ;
3、求目标事件的概率
变式 如图,有三个箱子,分别编号为1,2,3,其中1号箱有1个红球和4个白球, 2号箱有2个红球和3个白球, 3号箱有3个红球,这些球除了颜色外完全相同.现先从三箱中任取一箱,再从中任意摸出一球,发现是红球,求该球是取自1号箱的概率以及该球取自几号箱的可能性最大.
解:设表示事件“球取自第号箱”( =1,2,3), 表示事件“取得红球”,则有全概率公式,可得
= )+
=+ =
再由条件概率可得
= =
同理,
因此,该球取自1号箱的概率为,该球取自3号箱的概率最大.
设 , ,…, 为样本空间 的一个划分,若>0 ,)>0 ,则有:
贝叶斯公式
执果索因
(1) ,其中
(2) ∪… ∪ = .
贝叶斯公式的应用:
1、医疗决策与诊断
2、金融分析与风险管理
3、机器学习与人工智能(AI)
三、巩固新知
例1 现有12道题四选一的单选题,学生小张对其中9道题有思路,3道题完全没有思路.有思路的题做对的概率为0.9,没有思路的题只好猜一个答案,猜对的概率为0.25.小张从12道题中随机选择1道,求他做对该题的概率.
解:设=“选到有思路的题”,=“选到没有思路的题”,=“选到的题做对”,则=
由题可知:= = =
由全概率公式可得: +
= =
=
因此,小张做对选到的题的概率为0.7375.
例2 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
(2) 已知取到的是合格品,求它取自第一批产品的概率.
解:设=“取到的产品来自第批” ( =1,2) ,=“取到合格品”,则
(1)由全概率公式可得:
+
0.4 0.95+0.6 0.96=0.956
(2)由贝叶斯公式可得:
= ≈
, = 0 = 0
例1 采购员要购买某种电器元件一包(10个).他采购的方法是:从一包中随机抽查3个,如这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品,求采购员随机挑选一包拒绝购买的概率.
解:设=“取到的是含有4个次品的包”, =“取到的是含有1个次品的包”,表示事件“采购员拒绝购买”,则 ,样本空间的一个划分,且 .
由古典概型计算概率的公式可得:
= 1 = = 1 =
由全概率公式可得: +
= =
例2 甲乙丙三人同时对飞机进行射击,三人击中的概率分别为0.4,0.5,0.7.飞机被一人击中且击落的概率为0.2,被两人击中且击落的概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落的概率.
多个事件的全概率问题:化整为零
解:设表示事件“飞机被人击中”( =0,1,2,3), 表示事件“飞机被击落”,其中 , 构成样本空间的一个划分,则有=0, =0.2, =0.6, =1.
再设事件表示“飞机被第人击中” ( =1,2,3).
则= ∪
=∪
=
=
+=0.458
四、课堂小结
1、全概率
五、作业布置
课本P53: 第5题
2、贝叶斯公式:
7.1.2
全概率公式
学习目标
1.结合古典概型,会利用全概率公式计算概率.
2.了解贝叶斯公式.
3.核心素养:数学抽象、逻辑推理、数学运算.
一、复习导入
1.条件
2.概率的乘法公式:= =.
3.条件概率的性质:设>0,
(1)=1;
(2)如果B和C是两个互斥事件,则
+
(3)设和互为对立事件,则
二、新课讲授
问题1 如图,有三个箱子,分别编号为1,2,3,其中1号箱有1个红球和4个白球, 2号箱有2个红球和3个白球, 3号箱有3个红球,这些球除了颜色外完全相同.现先从三箱中任取一箱,再从中任意取出一球,求取得红球的概率.
分析:用表示事件“球取自第号箱”( =1,2,3), 表示事件“取得红球”,其中 , 互斥, 发生总是伴随着 , 之一同时发生,即= ∪,且两两互斥.
由互斥事件概率的加法公式可得:
= )+
再对求和中的每一项用乘法公式可得:
= )+
即= + =
设 是试验的样本空间, , ,…, 为样本空间的一组基事件,若
(1) ,其中
(2) ∪… ∪ = ,
则称 , ,…, 为样本空间的一个划分.
设 , ,…, 为样本空间 的一个划分,若)>0 ,则对任意一个事件有:
全概率公式
多因一果
(1) ,其中
(2) ∪… ∪ = .
对全概率公式的认识:
1、某一事件的发生可能有各种原因,如果是由原因互斥,构成一个完备事件)所引起,则发生的概率是发生概率的总和.
2、每一个原因都可能导致发生,故发生的概率是各种原因引起, 发生概率的总和即全概率公式.
3、全概率公式本质上是综合运用加法公式和乘法公式解决“多因一果”的概率问题.
问题2 某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录有如表的数据:
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
分析:用表示事件“所取到的产品是由第家元件制造厂提供的”( =1,2,3), 表示事件“取到的是一件次品”,其中 , 互斥,发生总是伴随着 , 之一同时发生,即= ∪,且两两互斥.
则有:= )+
)+
=+
=
因此,在仓库中随机地取一只元件,它是次品的概率是.
运用全概率公式的一般步骤:
1、求出样本空间 的一个划分 , ,…, ;
2、求 ;
3、求目标事件的概率
变式 如图,有三个箱子,分别编号为1,2,3,其中1号箱有1个红球和4个白球, 2号箱有2个红球和3个白球, 3号箱有3个红球,这些球除了颜色外完全相同.现先从三箱中任取一箱,再从中任意摸出一球,发现是红球,求该球是取自1号箱的概率以及该球取自几号箱的可能性最大.
解:设表示事件“球取自第号箱”( =1,2,3), 表示事件“取得红球”,则有全概率公式,可得
= )+
=+ =
再由条件概率可得
= =
同理,
因此,该球取自1号箱的概率为,该球取自3号箱的概率最大.
设 , ,…, 为样本空间 的一个划分,若>0 ,)>0 ,则有:
贝叶斯公式
执果索因
(1) ,其中
(2) ∪… ∪ = .
贝叶斯公式的应用:
1、医疗决策与诊断
2、金融分析与风险管理
3、机器学习与人工智能(AI)
三、巩固新知
例1 现有12道题四选一的单选题,学生小张对其中9道题有思路,3道题完全没有思路.有思路的题做对的概率为0.9,没有思路的题只好猜一个答案,猜对的概率为0.25.小张从12道题中随机选择1道,求他做对该题的概率.
解:设=“选到有思路的题”,=“选到没有思路的题”,=“选到的题做对”,则=
由题可知:= = =
由全概率公式可得: +
= =
=
因此,小张做对选到的题的概率为0.7375.
例2 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
(2) 已知取到的是合格品,求它取自第一批产品的概率.
解:设=“取到的产品来自第批” ( =1,2) ,=“取到合格品”,则
(1)由全概率公式可得:
+
0.4 0.95+0.6 0.96=0.956
(2)由贝叶斯公式可得:
= ≈
, = 0 = 0
例1 采购员要购买某种电器元件一包(10个).他采购的方法是:从一包中随机抽查3个,如这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品,求采购员随机挑选一包拒绝购买的概率.
解:设=“取到的是含有4个次品的包”, =“取到的是含有1个次品的包”,表示事件“采购员拒绝购买”,则 ,样本空间的一个划分,且 .
由古典概型计算概率的公式可得:
= 1 = = 1 =
由全概率公式可得: +
= =
例2 甲乙丙三人同时对飞机进行射击,三人击中的概率分别为0.4,0.5,0.7.飞机被一人击中且击落的概率为0.2,被两人击中且击落的概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落的概率.
多个事件的全概率问题:化整为零
解:设表示事件“飞机被人击中”( =0,1,2,3), 表示事件“飞机被击落”,其中 , 构成样本空间的一个划分,则有=0, =0.2, =0.6, =1.
再设事件表示“飞机被第人击中” ( =1,2,3).
则= ∪
=∪
=
=
+=0.458
四、课堂小结
1、全概率
五、作业布置
课本P53: 第5题
2、贝叶斯公式:
