苏教版四年级下册数学第七单元《三角形、平行四边形和梯形》检测卷(含答案解析)
文档属性
| 名称 | 苏教版四年级下册数学第七单元《三角形、平行四边形和梯形》检测卷(含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 231.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-29 10:07:04 | ||
图片预览




文档简介
四年级数学下册单元检测卷
第七单元《三角形、平行四边形和梯形》
姓名:_________ 班级:_________ 学号:_________
注意事项:
1.答题前填写好自己的班级、姓名等信息。
2.请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
卷面(2分)。我能做到书写工整,格式正确,卷面整洁。
一、知识空格填一填。(每空1分,共20分)
1.在一个三角形中,最多有( )个钝角,最多有( )个直角,最少有( )个锐角。
2.用三根小棒(取整厘米数)首尾相接围成一个三角形,已知其中两根小棒分别长9厘米和5厘米,第三根小棒最长( )厘米,最短( )厘米。
3.一个等腰三角形的底角是40°,它的顶角是( )°,按角分类,它是( )三角形;已知一个等腰三角形一条边长4厘米,另一条边长9厘米,那么这个等腰三角形的周长是( )厘米。
4.一根48厘米长的绳子,可以围成边长是( )厘米的等边三角形,等边三角形的一个内角是( )°。
5.王伯伯给自家一块等腰梯形菜地的四周围上栅栏,正好用了120米。已知梯形的上底长20米,一条腰长35米,下底长( )米。
6.一个梯形的下底是上底的2倍,如果将上底延长6厘米,就成了平行四边形,原来梯形的上底是( )厘米,下底是( )厘米。
7.把一个梯形按照下图的样子剪拼成一个三角形。如果梯形上底5厘米、下底是10厘米、高是6厘米,那么三角形的底是( )厘米,高是( )厘米。
8.三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是( )°。
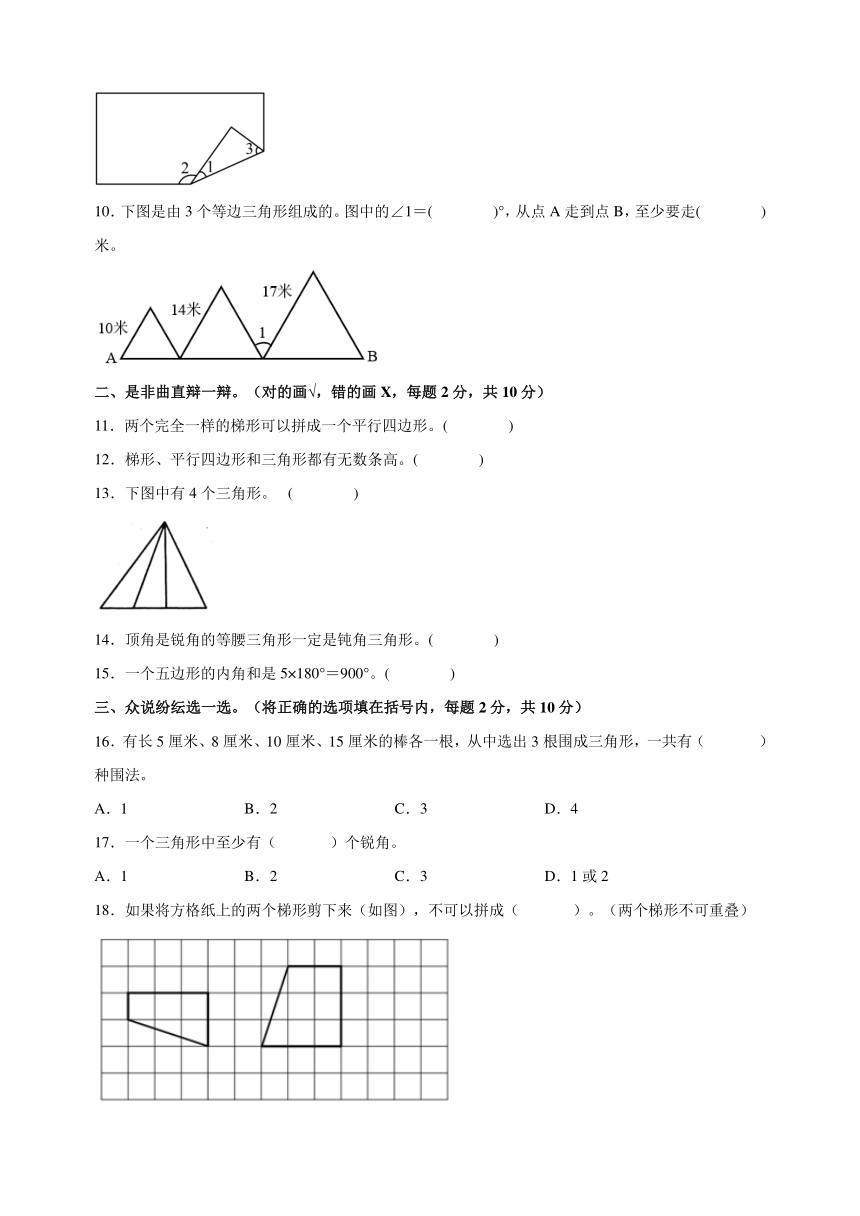
9.将一张长方形纸如图那样折起,已知∠2=120°,那么∠1=( )°,∠3=( )°。
10.下图是由3个等边三角形组成的。图中的∠1=( )°,从点A走到点B,至少要走( )米。
二、是非曲直辩一辩。(对的画√,错的画X,每题2分,共10分)
11.两个完全一样的梯形可以拼成一个平行四边形。( )
12.梯形、平行四边形和三角形都有无数条高。( )
13.下图中有4个三角形。 ( )
14.顶角是锐角的等腰三角形一定是钝角三角形。( )
15.一个五边形的内角和是5×180°=900°。( )
三、众说纷纭选一选。(将正确的选项填在括号内,每题2分,共10分)
16.有长5厘米、8厘米、10厘米、15厘米的棒各一根,从中选出3根围成三角形,一共有( )种围法。
A.1 B.2 C.3 D.4
17.一个三角形中至少有( )个锐角。
A.1 B.2 C.3 D.1或2
18.如果将方格纸上的两个梯形剪下来(如图),不可以拼成( )。(两个梯形不可重叠)
A.正方形 B.长方形 C.平行四边形 D.梯形
19.两个完全一样的梯形,上底是4厘米,下底是5厘米。两腰分别长3厘米和4厘米,若把它们拼成一个平行四边形,则这个平行四边形的周长可能是( )厘米。
A.24 B.22 C.30 D.23
20.下面说法错误的是( )。
①直角三角形中不存在比直角大的角;
②任意两个三角形都能拼成一个平行四边形;
③(28+72)×44和28+72×44的运算顺序不一样,但运算结果相同;
④用10倍的放大镜去看等边三角形,可以看到三个600°的角。
A.②③ B.①②④ C.②③④ D.③④
四、巧思妙想算一算。(共12分)
21.(本题6分)如图,已知∠1=127°,求∠2和∠3的度数。
22.(本题6分)如下图,等边三角形内有一个等腰三角形,并且∠1=∠2,∠3=∠4,求∠5。
五、手工作坊。(共12分)
23.(本题6分)画出下面图形指定底边上的高。
24.(本题6分)在下面的点子图中画一个底是3厘米、高是4厘米的平行四边形和一个上底是2厘米、下底是4厘米,高是3厘米的梯形。(每两点间的长度代表1厘米)
六、解决问题。(共36分)
25.(本题6分)把一根16厘米长的吸管剪成3段(每段都是整厘米数),围成一个三角形。你能围成几种不同的三角形?
26.(本题6分)一个等腰三角形有两条边的长度分别是17厘米和8厘米,这个等腰三角形的周长是多少厘米?
27.(本题6分)用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
28.(本题6分)一个平行四边形的周长是20厘米,相邻的两条边相差2厘米。相邻的两条边的长度分别是多少厘米?
29.(本题6分)一个等边三角形菜园的周长与一个正方形花圃的周长相等,这个花圃的边长是15米,菜园的边长是多少米?
30.(本题6分)一个等腰三角形的底角是顶角的2倍,这个等腰三角形的底角和顶角分别是多少?
参考答案
一、知识空格填一填。
1.1 1 2
【分析】①根据三角形的内角和是180°可知,如果一个三角形中出现2个或3个钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°;
②如果一个三角形中出现2个或3个直角,再加上第三个角,那么三角形的内角和就大于180°,也不符合三角形内角和是180°;
③所以,三角形中最多有一个钝角或直角,最少有两个锐角,一个三角形中最多有3个锐角,如锐角三角形;据此解答。
【详解】根据分析:在一个三角形中,最多有1个钝角,最多有1个直角,最少有2个锐角。
【点睛】明确三角形内角和是解答此题的关键。
2.13 5
【分析】三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边,据此解答。
【详解】9+5=14(厘米)
9-5=4(厘米)
4厘米<第三根小棒的长度<14厘米
第三根小棒最长13厘米,最短5厘米。
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
3.100 钝角 22
【分析】等腰三角形两腰相等,两底角也相等,三角形的内角和是180°,用180°减去40°再减去40°即是这个等腰三角形的顶角度数。按角分类,三角形有直角三角形、锐角三角形、钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形。三角形任意两边之和大于第三边,据此判断这个等腰三角形第三条边长度,这个等腰三角形第三条边长度如果是4厘米,有4+4<9,不能围成三角形,所以这个等腰三角形第三条边长度是9厘米,将三条边的长度相加即可。
【详解】180°-40°-40°
=140°-40°
=100°
100°的角是钝角,按角分类这个等腰三角形是钝角三角形。
4+9+9
=13+9
=22(厘米)
一个等腰三角形的底角是40°,它的顶角是100°,按角分类,它是钝角三角形;已知一个等腰三角形一条边长4厘米,另一条边长9厘米,那么这个等腰三角形的周长是22厘米。
【点睛】此题考查了三角形的内角和、三角形的三边关系及三角形的分类,属于基础题,应熟练掌握。
4.16 60
【分析】等边三角形的3条边都相等,用48除以3,求出每条边的长度;等边三角形的3个内角都相等,用180°除以3,求出它的一个内角。
【详解】48÷3=16(厘米)
180°÷3=60°
则一根48厘米长的绳子,可以围成边长是16厘米的等边三角形,等边三角形的一个内角是60°。
【点睛】熟练掌握等边三角形的特征以及三角形的内角和定理是解答此题的关键。
5.30
【分析】等腰梯形的两腰相等,栅栏的长度即为这个梯形的周长,35乘2算出两腰的和,周长减上底,所得差再减两腰的和即可求出下底。
【详解】120-20-35×2
=120-20-70
=100-70
=30(米)
【点睛】栅栏的长度即为梯形周长,周长即梯形4条边的和。
6.6 12
【分析】平行四边形的对边相等,梯形的下底是上底的2倍,即上底是下底的一半,上底延长的6厘米也是梯形的上底长度,故梯形的下底长度为6的2倍,据此解答。
【详解】6×2=12(厘米)
梯形的上底是6厘米,下底是12厘米。
【点睛】上底延长6厘米后与梯形的下底相等,即梯形下底是6厘米的2倍。
7.15 6
【分析】根据题意可知:把梯形剪拼成三角形,三角形的底等于梯形上、下底之和,三角形的高等于梯形的高,据此解答即可。
【详解】由分析得:把梯形剪拼成三角形,三角形的底等于梯形上、下底之和,三角形的高等于梯形的高。
5+10=15(厘米)
三角形的底是15厘米,高是6厘米。
【点睛】此题考查的目的是理解掌握梯形、三角形的特征及应用。
8.360
【分析】三角形截取一个角后,得到的是四边形,根据内角和定理即可求解。
【详解】剩下部分是四边形,四边形的内角和是360°。
【点睛】本题解题的关键是能理解一个三角形截取一个角后得到的图形的形状。
9.30 60
【分析】观察下图可知,∠1等于∠4,180度减∠2等于∠1与∠4的和,再除以2等于∠1的度数,三角形内角和等于180度,所以180度减∠1,再减90度即等于∠3的度数。
【详解】∠1=∠4
∠1=(180°-∠2)÷2
=(180°-120°)÷2
=60°÷2
=30°
∠3=180°-90°-∠1
=90°-30°
=60°
【点睛】熟练掌握三角形内角和和角的分类知识是解答本题的关键。
10.60 41
【分析】等边三角形的三条边相等,三个内角都是60°,和∠1相邻的两个角都是60°,180°减60°,再减60°即可求出∠1的度数。要求从点A走到点B的长度,组成线段AB的三条线段的长度分别为10米、14米、17米,把这三个数相加即可。
【详解】∠1=60°
10+14+17
=24+17
=41(米)
【点睛】等边三角形的三条边相等,三个内角也相等都是60°。1平角=180°。
二、是非曲直辩一辩。
11.√
【分析】因平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
【详解】如图所示:
因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形,故原题的说法正确。
故答案为:√
【点睛】本题的关键是根据平行四边形的特征来判断,组合后图形是不是符合平行四边形的特征。
12.×
【分析】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。则梯形有无数条高。
从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。则平行四边形有无数条高。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。则三角形有三条高。
【详解】梯形和平行四边形有无数条高,三角形有3条高。
故答案为:×。
【点睛】本题考查梯形、平行四边形和三角形的高,注意三角形只有3条高。
13.×
【解析】略
14.×
【分析】由已知等腰三角形顶角是锐角,结合等腰三角形的两底角相等,根据三角形内角和是180度,用“(180-锐角)”解答即可得到底角度数小于90°;然后根据三角形的分类进行解答即可。
【详解】因为等腰三角形顶角是锐角,
则其底角度数为:(180-锐角)÷2<90°,即为锐角,
所以这个三角形一定是锐角三角形;
故答案为:×
【点睛】本题考查了等腰三角形的性质及三角形内角和定理。
15.×
【分析】过一个顶点连接五边形的对角线,可将五边形分成3个三角形,180°乘3即可知道五边形的内角和。
【详解】内角和是180°×3=540°
故答案为:×
【点睛】三角形的内角是180°,求多边形的内角和,可将多边形的对角线相连,能将多边形分成几个三角形,再根据三角形的内角和求出多边形的内角和。
三、众说纷纭选一选。
16.B
【分析】根据三角形三边关系:三角形任意两边之和大于第三边;据此从5厘米开始选择不同长度的小棒,满足三边之间的关系,有几种选法就有几种围法。
【详解】5+8>10,选取5厘米、8厘米、10厘米的小棒可以围成三角形;
8+10>15,选取8厘米、10厘米、15厘米的小棒可以围成三角形。
一共有2种围法。
有长5厘米、8厘米、10厘米、15厘米的棒各一根,从中选出3根围成三角形,一共有2种围法。
故答案为:B
【点睛】解答本题的关键是理解和掌握三角形三边的关系。
17.B
【分析】假设一个三角形中只有一个锐角,另两个角都大于等于90度,则三个角的和大于180度,这与三角形内角和等于180度相矛盾,所以一个三角形中至少有2个锐角,据此即可解答。
【详解】根据分析可知,一个三角形中至少有2个锐角。
故答案为:B
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
18.A
【分析】若左边梯形的下底和右边梯形的上底拼在一起,可以拼成一个梯形。若左边梯形的直角边和右边梯形的直角边拼在一起,可以拼成一个平行四边形。若左边梯形的腰和右边梯形的腰拼在一起,可以拼成一个长方形,据此解答。
【详解】由分析得:
这两个梯形不可以拼成正方形,可以拼成长方形、平行四边形和梯形。
故答案为:A
【点睛】本题考查图形的拼接,可以将长度相等的边拼在一起,看能拼成什么形状。可以亲自动手拼一拼,即可得出结论。
19.A
【分析】根据题意可得,这个平行四边形的两条邻边分别长:5+4=9(厘米)、3厘米,或5+4=9(厘米)、4厘米。然后根据这个平行四边形的周长=两条邻边的长度和×2
解答即可。
【详解】拼成的平行四边形的两条邻边分别长:
5+4=9(厘米)、3厘米,或5+4=9(厘米)、4厘米。
所以周长可能是:
(9+3)×2
=12×2
=24(厘米)
(9+4)×2
=13×2
=26(厘米)
这个平行四边形的周长可能是24厘米或26厘米。
故答案为:A
【点睛】解答本题关键是确定这个平行四边形的两条邻边的长度。
20.C
【分析】①三角形最大的角是什么角,这个三角形就是什么三角形;
②平行四边形可以分成两个完全相同的三角形;
③第一个式子先算加法,再算乘法;第二个式子先算乘法,再算加法;运算顺序不同,分别计算出两个式子的得数,再比较;
④在10倍放大镜下看等边三角形,角两边的张口大小不变,所以角的大小不变。
【详解】①直角三角形中最大的角是直角,所以这句话正确;
②只有完全相同的两个三角形可以拼成一个平行四边形,所以这句话不对;
③(28+72)×44
=100×44
=4400
28+72×44
=28+3168
=3196
运算顺序不同,运算结果也不同,所以这句话不对;
④用10倍的放大镜去看等边三角形,三个内角还是60°,所以这句话不对。
故答案为:C
【点睛】角两边的张口越大角越大,角的大小与角两边的长短无关。
四、巧思妙想算一算。
21.∠2=37°;∠3=53°
【分析】如下图,∠4等于180°减∠1,∠2和∠4是直角三角形中的两个锐角,所以∠2等于90°减∠4,∠3和∠2也是直角三角形的两个锐角,所以∠3等于90°减∠2,据此即可解答。
【详解】∠4=180°-127°=53°
∠2=90°-∠4
=90°-53°
=37°
∠3=90°-∠2
=90°-37°
=53°
22.120°
【分析】等边三角形的三个内角都等于60°,∠1=∠2,∠3=∠4,所以∠1=60°÷2=30°,∠3=60°÷2=30°,∠5=180°-∠1-∠3,据此即可解答。
【详解】∠1+∠2=60°,∠3+∠4=60°
∠1=∠2,∠3=∠4
所以∠1=60°÷2=30°,∠3=60°÷2=30°
∠5=180°-∠1-∠3=180°-30°-30°=120°
五、手工作坊。
23.见详解
【分析】(1)从与三角形底边相对的顶点作底边的垂线段,即为底边上的高;
(2)从梯形一条底边上一点作另一底边的垂线段,即为梯形的高;
(3)从平行四边形底边的对边上一点作底边的垂线段,即底边上的高。
【详解】
【点睛】本题主要考查学生画三角形、梯形和平行四边形高的方法的掌握。
24.见详解
【分析】(1)先画两条平行的线段,长度都为3厘米,两条平行线段之间的距离为4厘米,再把两条线段对应端点连结起来即可。
(2)先画两条平行的线段,上面一条长为2厘米,下面一条长为4厘米,两条平行线段之间的距离为3厘米,再把两条线段对应端点连结起来即可。
【详解】
【点睛】本题主要考查学生画平行四边形和梯形方法的掌握和灵活运用。
六、解决问题。
25.5种
【分析】这3段吸管的长度和为16厘米。根据三角形的三边关系可知,16÷2=8(厘米),最长的吸管应小于8厘米,最长是7厘米。当最长的吸管长7厘米时,其余两根吸管可以长7厘米、2厘米或者6厘米、3厘米或者5厘米、4厘米;当最长的吸管长6厘米时,其余两根吸管可以长5厘米、5厘米或者6厘米、4厘米。据此解答即可。
【详解】三边分别为:①2厘米、7厘米、7厘米;②3厘米、6厘米、7厘米;③4厘米、5厘米、7厘米;④5厘米、5厘米、6厘米;⑤4厘米、6厘米、6厘米;
答:能围成5种不同的三角形。
【点睛】本题考查三角形的三边关系:三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。
26.42厘米
【分析】已知两条边分别长17厘米和8厘米,如果长17厘米的边是这个三角形的底,那么长8厘米的边就是它的腰,另一条腰也是8厘米,根据三角形的基本性质“两边之和大于第三边”,而8+8=16,这不满足这一性质,所以这个三角形的底是8厘米,腰是17厘米,再把等腰三角形三边相加即可,据此解答。
【详解】由分析可得:
17+17+8
=34+8
=42(厘米)
答:等腰三角形的周长是42厘米。
【点睛】熟练掌握三角形的三边关系及三角形周长的求法是本题解答的关键。
27.60厘米
【分析】等腰梯形的两条腰相等,梯形的周长减去两个底的长度等于两条腰的长度,再除以2即等于一条腰长,据此即可解答。
【详解】(217-31-66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点睛】本题主要考查学生对梯形的周长和分类知识的掌握。
28.4厘米和6厘米
【分析】用20除以2,求出相邻两条边的长度之和;用相邻两条边的长度之和减去2的差,再除以2,求出较短的边;用较短的边加上2,求出较长的边。
【详解】20÷2=10(厘米)
(10-2)÷2
=8÷2
=4(厘米)
4+2=6(厘米)
答:相邻的两条边的长度分别是4厘米和6厘米。
【点睛】解答此题,首先弄清题意,分清已知与所求,再找出基本数量关系,由此列式解答。
29.20米
【分析】用15乘4,求出正方形花圃的周长;因为一个等边三角形菜园的周长与一个正方形花圃的周长相等,用正方形花圃的周长除以3,求出菜园的边长。
【详解】15×4÷3
=60÷3
=20(米)
答:菜园的边长是20米。
【点睛】等边三角形的3条边都相等,是解答此题的关键。
30.底角72°;底角36°
【分析】等腰三角形的两个底角相等。根据三角形的内角和为180°可知,顶角+2×底角=180°。根据“底角是顶角的2倍”,则5个顶角是180°,顶角为180°÷5。再用顶角乘2,即可求出底角。
【详解】180°÷(1+2+2)
=180°÷5
=36°
36°×2=72°
答:这个等腰三角形的底角和顶角分别是72°和36°。
【点睛】本题考查等腰三角形的性质和三角形的内角和,关键是明确5个顶角是180°。
第七单元《三角形、平行四边形和梯形》
姓名:_________ 班级:_________ 学号:_________
注意事项:
1.答题前填写好自己的班级、姓名等信息。
2.请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
卷面(2分)。我能做到书写工整,格式正确,卷面整洁。
一、知识空格填一填。(每空1分,共20分)
1.在一个三角形中,最多有( )个钝角,最多有( )个直角,最少有( )个锐角。
2.用三根小棒(取整厘米数)首尾相接围成一个三角形,已知其中两根小棒分别长9厘米和5厘米,第三根小棒最长( )厘米,最短( )厘米。
3.一个等腰三角形的底角是40°,它的顶角是( )°,按角分类,它是( )三角形;已知一个等腰三角形一条边长4厘米,另一条边长9厘米,那么这个等腰三角形的周长是( )厘米。
4.一根48厘米长的绳子,可以围成边长是( )厘米的等边三角形,等边三角形的一个内角是( )°。
5.王伯伯给自家一块等腰梯形菜地的四周围上栅栏,正好用了120米。已知梯形的上底长20米,一条腰长35米,下底长( )米。
6.一个梯形的下底是上底的2倍,如果将上底延长6厘米,就成了平行四边形,原来梯形的上底是( )厘米,下底是( )厘米。
7.把一个梯形按照下图的样子剪拼成一个三角形。如果梯形上底5厘米、下底是10厘米、高是6厘米,那么三角形的底是( )厘米,高是( )厘米。
8.三角形中有一个角是45°,如果剪去这个角(如图),剩下部分的内角和是( )°。
9.将一张长方形纸如图那样折起,已知∠2=120°,那么∠1=( )°,∠3=( )°。
10.下图是由3个等边三角形组成的。图中的∠1=( )°,从点A走到点B,至少要走( )米。
二、是非曲直辩一辩。(对的画√,错的画X,每题2分,共10分)
11.两个完全一样的梯形可以拼成一个平行四边形。( )
12.梯形、平行四边形和三角形都有无数条高。( )
13.下图中有4个三角形。 ( )
14.顶角是锐角的等腰三角形一定是钝角三角形。( )
15.一个五边形的内角和是5×180°=900°。( )
三、众说纷纭选一选。(将正确的选项填在括号内,每题2分,共10分)
16.有长5厘米、8厘米、10厘米、15厘米的棒各一根,从中选出3根围成三角形,一共有( )种围法。
A.1 B.2 C.3 D.4
17.一个三角形中至少有( )个锐角。
A.1 B.2 C.3 D.1或2
18.如果将方格纸上的两个梯形剪下来(如图),不可以拼成( )。(两个梯形不可重叠)
A.正方形 B.长方形 C.平行四边形 D.梯形
19.两个完全一样的梯形,上底是4厘米,下底是5厘米。两腰分别长3厘米和4厘米,若把它们拼成一个平行四边形,则这个平行四边形的周长可能是( )厘米。
A.24 B.22 C.30 D.23
20.下面说法错误的是( )。
①直角三角形中不存在比直角大的角;
②任意两个三角形都能拼成一个平行四边形;
③(28+72)×44和28+72×44的运算顺序不一样,但运算结果相同;
④用10倍的放大镜去看等边三角形,可以看到三个600°的角。
A.②③ B.①②④ C.②③④ D.③④
四、巧思妙想算一算。(共12分)
21.(本题6分)如图,已知∠1=127°,求∠2和∠3的度数。
22.(本题6分)如下图,等边三角形内有一个等腰三角形,并且∠1=∠2,∠3=∠4,求∠5。
五、手工作坊。(共12分)
23.(本题6分)画出下面图形指定底边上的高。
24.(本题6分)在下面的点子图中画一个底是3厘米、高是4厘米的平行四边形和一个上底是2厘米、下底是4厘米,高是3厘米的梯形。(每两点间的长度代表1厘米)
六、解决问题。(共36分)
25.(本题6分)把一根16厘米长的吸管剪成3段(每段都是整厘米数),围成一个三角形。你能围成几种不同的三角形?
26.(本题6分)一个等腰三角形有两条边的长度分别是17厘米和8厘米,这个等腰三角形的周长是多少厘米?
27.(本题6分)用一根217厘米长的铁丝正好围成一个等腰梯形。梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?
28.(本题6分)一个平行四边形的周长是20厘米,相邻的两条边相差2厘米。相邻的两条边的长度分别是多少厘米?
29.(本题6分)一个等边三角形菜园的周长与一个正方形花圃的周长相等,这个花圃的边长是15米,菜园的边长是多少米?
30.(本题6分)一个等腰三角形的底角是顶角的2倍,这个等腰三角形的底角和顶角分别是多少?
参考答案
一、知识空格填一填。
1.1 1 2
【分析】①根据三角形的内角和是180°可知,如果一个三角形中出现2个或3个钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°;
②如果一个三角形中出现2个或3个直角,再加上第三个角,那么三角形的内角和就大于180°,也不符合三角形内角和是180°;
③所以,三角形中最多有一个钝角或直角,最少有两个锐角,一个三角形中最多有3个锐角,如锐角三角形;据此解答。
【详解】根据分析:在一个三角形中,最多有1个钝角,最多有1个直角,最少有2个锐角。
【点睛】明确三角形内角和是解答此题的关键。
2.13 5
【分析】三角形的三边关系:两边之和大于第三条边,两边之差小于第三条边,据此解答。
【详解】9+5=14(厘米)
9-5=4(厘米)
4厘米<第三根小棒的长度<14厘米
第三根小棒最长13厘米,最短5厘米。
【点睛】熟练掌握三角形的三边关系是解答此题的关键。
3.100 钝角 22
【分析】等腰三角形两腰相等,两底角也相等,三角形的内角和是180°,用180°减去40°再减去40°即是这个等腰三角形的顶角度数。按角分类,三角形有直角三角形、锐角三角形、钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形。三角形任意两边之和大于第三边,据此判断这个等腰三角形第三条边长度,这个等腰三角形第三条边长度如果是4厘米,有4+4<9,不能围成三角形,所以这个等腰三角形第三条边长度是9厘米,将三条边的长度相加即可。
【详解】180°-40°-40°
=140°-40°
=100°
100°的角是钝角,按角分类这个等腰三角形是钝角三角形。
4+9+9
=13+9
=22(厘米)
一个等腰三角形的底角是40°,它的顶角是100°,按角分类,它是钝角三角形;已知一个等腰三角形一条边长4厘米,另一条边长9厘米,那么这个等腰三角形的周长是22厘米。
【点睛】此题考查了三角形的内角和、三角形的三边关系及三角形的分类,属于基础题,应熟练掌握。
4.16 60
【分析】等边三角形的3条边都相等,用48除以3,求出每条边的长度;等边三角形的3个内角都相等,用180°除以3,求出它的一个内角。
【详解】48÷3=16(厘米)
180°÷3=60°
则一根48厘米长的绳子,可以围成边长是16厘米的等边三角形,等边三角形的一个内角是60°。
【点睛】熟练掌握等边三角形的特征以及三角形的内角和定理是解答此题的关键。
5.30
【分析】等腰梯形的两腰相等,栅栏的长度即为这个梯形的周长,35乘2算出两腰的和,周长减上底,所得差再减两腰的和即可求出下底。
【详解】120-20-35×2
=120-20-70
=100-70
=30(米)
【点睛】栅栏的长度即为梯形周长,周长即梯形4条边的和。
6.6 12
【分析】平行四边形的对边相等,梯形的下底是上底的2倍,即上底是下底的一半,上底延长的6厘米也是梯形的上底长度,故梯形的下底长度为6的2倍,据此解答。
【详解】6×2=12(厘米)
梯形的上底是6厘米,下底是12厘米。
【点睛】上底延长6厘米后与梯形的下底相等,即梯形下底是6厘米的2倍。
7.15 6
【分析】根据题意可知:把梯形剪拼成三角形,三角形的底等于梯形上、下底之和,三角形的高等于梯形的高,据此解答即可。
【详解】由分析得:把梯形剪拼成三角形,三角形的底等于梯形上、下底之和,三角形的高等于梯形的高。
5+10=15(厘米)
三角形的底是15厘米,高是6厘米。
【点睛】此题考查的目的是理解掌握梯形、三角形的特征及应用。
8.360
【分析】三角形截取一个角后,得到的是四边形,根据内角和定理即可求解。
【详解】剩下部分是四边形,四边形的内角和是360°。
【点睛】本题解题的关键是能理解一个三角形截取一个角后得到的图形的形状。
9.30 60
【分析】观察下图可知,∠1等于∠4,180度减∠2等于∠1与∠4的和,再除以2等于∠1的度数,三角形内角和等于180度,所以180度减∠1,再减90度即等于∠3的度数。
【详解】∠1=∠4
∠1=(180°-∠2)÷2
=(180°-120°)÷2
=60°÷2
=30°
∠3=180°-90°-∠1
=90°-30°
=60°
【点睛】熟练掌握三角形内角和和角的分类知识是解答本题的关键。
10.60 41
【分析】等边三角形的三条边相等,三个内角都是60°,和∠1相邻的两个角都是60°,180°减60°,再减60°即可求出∠1的度数。要求从点A走到点B的长度,组成线段AB的三条线段的长度分别为10米、14米、17米,把这三个数相加即可。
【详解】∠1=60°
10+14+17
=24+17
=41(米)
【点睛】等边三角形的三条边相等,三个内角也相等都是60°。1平角=180°。
二、是非曲直辩一辩。
11.√
【分析】因平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
【详解】如图所示:
因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形,故原题的说法正确。
故答案为:√
【点睛】本题的关键是根据平行四边形的特征来判断,组合后图形是不是符合平行四边形的特征。
12.×
【分析】从梯形一条底边上的一点到它对边的垂直线段叫做梯形的高。则梯形有无数条高。
从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。则平行四边形有无数条高。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。则三角形有三条高。
【详解】梯形和平行四边形有无数条高,三角形有3条高。
故答案为:×。
【点睛】本题考查梯形、平行四边形和三角形的高,注意三角形只有3条高。
13.×
【解析】略
14.×
【分析】由已知等腰三角形顶角是锐角,结合等腰三角形的两底角相等,根据三角形内角和是180度,用“(180-锐角)”解答即可得到底角度数小于90°;然后根据三角形的分类进行解答即可。
【详解】因为等腰三角形顶角是锐角,
则其底角度数为:(180-锐角)÷2<90°,即为锐角,
所以这个三角形一定是锐角三角形;
故答案为:×
【点睛】本题考查了等腰三角形的性质及三角形内角和定理。
15.×
【分析】过一个顶点连接五边形的对角线,可将五边形分成3个三角形,180°乘3即可知道五边形的内角和。
【详解】内角和是180°×3=540°
故答案为:×
【点睛】三角形的内角是180°,求多边形的内角和,可将多边形的对角线相连,能将多边形分成几个三角形,再根据三角形的内角和求出多边形的内角和。
三、众说纷纭选一选。
16.B
【分析】根据三角形三边关系:三角形任意两边之和大于第三边;据此从5厘米开始选择不同长度的小棒,满足三边之间的关系,有几种选法就有几种围法。
【详解】5+8>10,选取5厘米、8厘米、10厘米的小棒可以围成三角形;
8+10>15,选取8厘米、10厘米、15厘米的小棒可以围成三角形。
一共有2种围法。
有长5厘米、8厘米、10厘米、15厘米的棒各一根,从中选出3根围成三角形,一共有2种围法。
故答案为:B
【点睛】解答本题的关键是理解和掌握三角形三边的关系。
17.B
【分析】假设一个三角形中只有一个锐角,另两个角都大于等于90度,则三个角的和大于180度,这与三角形内角和等于180度相矛盾,所以一个三角形中至少有2个锐角,据此即可解答。
【详解】根据分析可知,一个三角形中至少有2个锐角。
故答案为:B
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
18.A
【分析】若左边梯形的下底和右边梯形的上底拼在一起,可以拼成一个梯形。若左边梯形的直角边和右边梯形的直角边拼在一起,可以拼成一个平行四边形。若左边梯形的腰和右边梯形的腰拼在一起,可以拼成一个长方形,据此解答。
【详解】由分析得:
这两个梯形不可以拼成正方形,可以拼成长方形、平行四边形和梯形。
故答案为:A
【点睛】本题考查图形的拼接,可以将长度相等的边拼在一起,看能拼成什么形状。可以亲自动手拼一拼,即可得出结论。
19.A
【分析】根据题意可得,这个平行四边形的两条邻边分别长:5+4=9(厘米)、3厘米,或5+4=9(厘米)、4厘米。然后根据这个平行四边形的周长=两条邻边的长度和×2
解答即可。
【详解】拼成的平行四边形的两条邻边分别长:
5+4=9(厘米)、3厘米,或5+4=9(厘米)、4厘米。
所以周长可能是:
(9+3)×2
=12×2
=24(厘米)
(9+4)×2
=13×2
=26(厘米)
这个平行四边形的周长可能是24厘米或26厘米。
故答案为:A
【点睛】解答本题关键是确定这个平行四边形的两条邻边的长度。
20.C
【分析】①三角形最大的角是什么角,这个三角形就是什么三角形;
②平行四边形可以分成两个完全相同的三角形;
③第一个式子先算加法,再算乘法;第二个式子先算乘法,再算加法;运算顺序不同,分别计算出两个式子的得数,再比较;
④在10倍放大镜下看等边三角形,角两边的张口大小不变,所以角的大小不变。
【详解】①直角三角形中最大的角是直角,所以这句话正确;
②只有完全相同的两个三角形可以拼成一个平行四边形,所以这句话不对;
③(28+72)×44
=100×44
=4400
28+72×44
=28+3168
=3196
运算顺序不同,运算结果也不同,所以这句话不对;
④用10倍的放大镜去看等边三角形,三个内角还是60°,所以这句话不对。
故答案为:C
【点睛】角两边的张口越大角越大,角的大小与角两边的长短无关。
四、巧思妙想算一算。
21.∠2=37°;∠3=53°
【分析】如下图,∠4等于180°减∠1,∠2和∠4是直角三角形中的两个锐角,所以∠2等于90°减∠4,∠3和∠2也是直角三角形的两个锐角,所以∠3等于90°减∠2,据此即可解答。
【详解】∠4=180°-127°=53°
∠2=90°-∠4
=90°-53°
=37°
∠3=90°-∠2
=90°-37°
=53°
22.120°
【分析】等边三角形的三个内角都等于60°,∠1=∠2,∠3=∠4,所以∠1=60°÷2=30°,∠3=60°÷2=30°,∠5=180°-∠1-∠3,据此即可解答。
【详解】∠1+∠2=60°,∠3+∠4=60°
∠1=∠2,∠3=∠4
所以∠1=60°÷2=30°,∠3=60°÷2=30°
∠5=180°-∠1-∠3=180°-30°-30°=120°
五、手工作坊。
23.见详解
【分析】(1)从与三角形底边相对的顶点作底边的垂线段,即为底边上的高;
(2)从梯形一条底边上一点作另一底边的垂线段,即为梯形的高;
(3)从平行四边形底边的对边上一点作底边的垂线段,即底边上的高。
【详解】
【点睛】本题主要考查学生画三角形、梯形和平行四边形高的方法的掌握。
24.见详解
【分析】(1)先画两条平行的线段,长度都为3厘米,两条平行线段之间的距离为4厘米,再把两条线段对应端点连结起来即可。
(2)先画两条平行的线段,上面一条长为2厘米,下面一条长为4厘米,两条平行线段之间的距离为3厘米,再把两条线段对应端点连结起来即可。
【详解】
【点睛】本题主要考查学生画平行四边形和梯形方法的掌握和灵活运用。
六、解决问题。
25.5种
【分析】这3段吸管的长度和为16厘米。根据三角形的三边关系可知,16÷2=8(厘米),最长的吸管应小于8厘米,最长是7厘米。当最长的吸管长7厘米时,其余两根吸管可以长7厘米、2厘米或者6厘米、3厘米或者5厘米、4厘米;当最长的吸管长6厘米时,其余两根吸管可以长5厘米、5厘米或者6厘米、4厘米。据此解答即可。
【详解】三边分别为:①2厘米、7厘米、7厘米;②3厘米、6厘米、7厘米;③4厘米、5厘米、7厘米;④5厘米、5厘米、6厘米;⑤4厘米、6厘米、6厘米;
答:能围成5种不同的三角形。
【点睛】本题考查三角形的三边关系:三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。
26.42厘米
【分析】已知两条边分别长17厘米和8厘米,如果长17厘米的边是这个三角形的底,那么长8厘米的边就是它的腰,另一条腰也是8厘米,根据三角形的基本性质“两边之和大于第三边”,而8+8=16,这不满足这一性质,所以这个三角形的底是8厘米,腰是17厘米,再把等腰三角形三边相加即可,据此解答。
【详解】由分析可得:
17+17+8
=34+8
=42(厘米)
答:等腰三角形的周长是42厘米。
【点睛】熟练掌握三角形的三边关系及三角形周长的求法是本题解答的关键。
27.60厘米
【分析】等腰梯形的两条腰相等,梯形的周长减去两个底的长度等于两条腰的长度,再除以2即等于一条腰长,据此即可解答。
【详解】(217-31-66)÷2
=120÷2
=60(厘米)
答:它的一条腰长60厘米。
【点睛】本题主要考查学生对梯形的周长和分类知识的掌握。
28.4厘米和6厘米
【分析】用20除以2,求出相邻两条边的长度之和;用相邻两条边的长度之和减去2的差,再除以2,求出较短的边;用较短的边加上2,求出较长的边。
【详解】20÷2=10(厘米)
(10-2)÷2
=8÷2
=4(厘米)
4+2=6(厘米)
答:相邻的两条边的长度分别是4厘米和6厘米。
【点睛】解答此题,首先弄清题意,分清已知与所求,再找出基本数量关系,由此列式解答。
29.20米
【分析】用15乘4,求出正方形花圃的周长;因为一个等边三角形菜园的周长与一个正方形花圃的周长相等,用正方形花圃的周长除以3,求出菜园的边长。
【详解】15×4÷3
=60÷3
=20(米)
答:菜园的边长是20米。
【点睛】等边三角形的3条边都相等,是解答此题的关键。
30.底角72°;底角36°
【分析】等腰三角形的两个底角相等。根据三角形的内角和为180°可知,顶角+2×底角=180°。根据“底角是顶角的2倍”,则5个顶角是180°,顶角为180°÷5。再用顶角乘2,即可求出底角。
【详解】180°÷(1+2+2)
=180°÷5
=36°
36°×2=72°
答:这个等腰三角形的底角和顶角分别是72°和36°。
【点睛】本题考查等腰三角形的性质和三角形的内角和,关键是明确5个顶角是180°。
