2015秋鲁教版数学八上1.3《公式法》ppt课件
文档属性
| 名称 | 2015秋鲁教版数学八上1.3《公式法》ppt课件 |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-10 00:00:00 | ||
图片预览



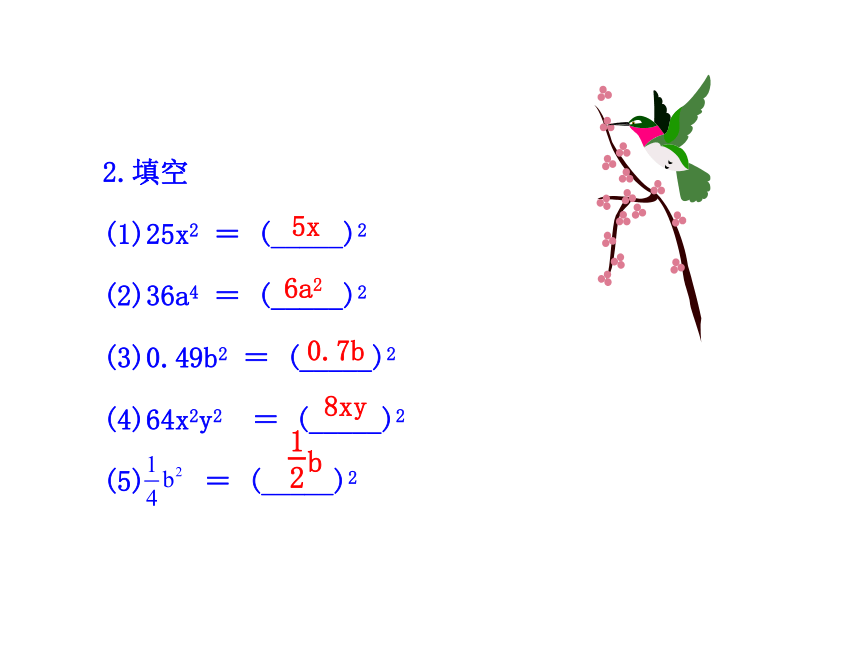




文档简介
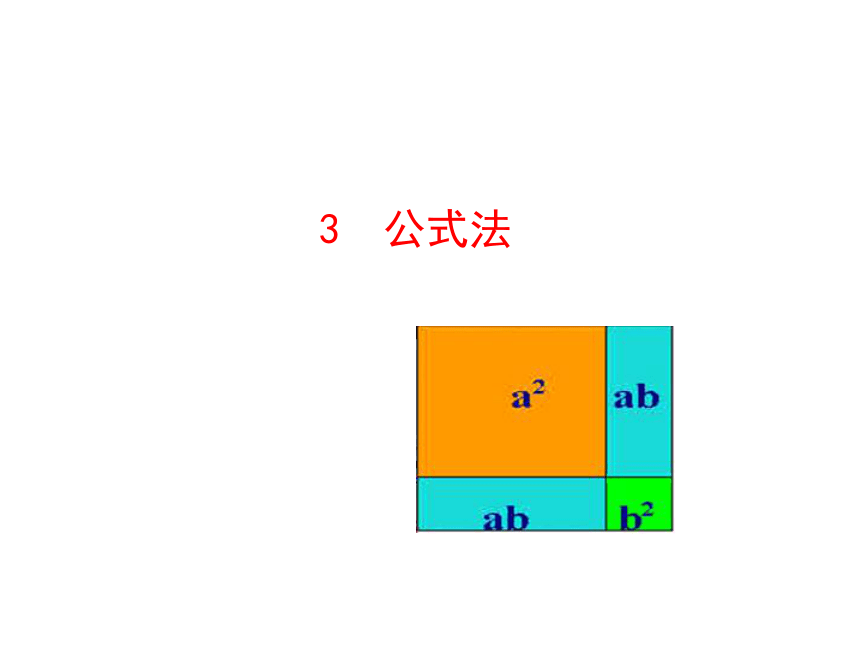
(共22张PPT)
3 公式法
1.使学生了解运用公式法因式分解的意义.
2.使学生掌握运用平方差公式因式分解.
3.使学生会用完全平方公式因式分解,进一步发展符号感和推理能力.
一 看系数 二 看字母 三 看指数
最大公约数
相同字母 相同字母的最低次幂
1.把下列各式因式分解:
(1)3a3b2-12ab3
(2)x(a+b)+y(a+b)
(3)a(m-2)+b(2-m)
(4)a(x-y)2-b(y-x)2
【温故知新】
2.填空
(1)25x2 = (_____)2
(2)36a4 = (_____)2
(3)0.49b2 = (_____)2
(4)64x2y2 = (_____)2
(5) = (_____)2
5x
6a2
0.7b
8xy
(1)(x+5)(x-5)=____________
(2)(3x-y)(3x+y)=___________
(3)(1+3a)(1-3a)=___________
(整式乘法)
(因式分解)
1-9a2
x2-25
9x2-y2
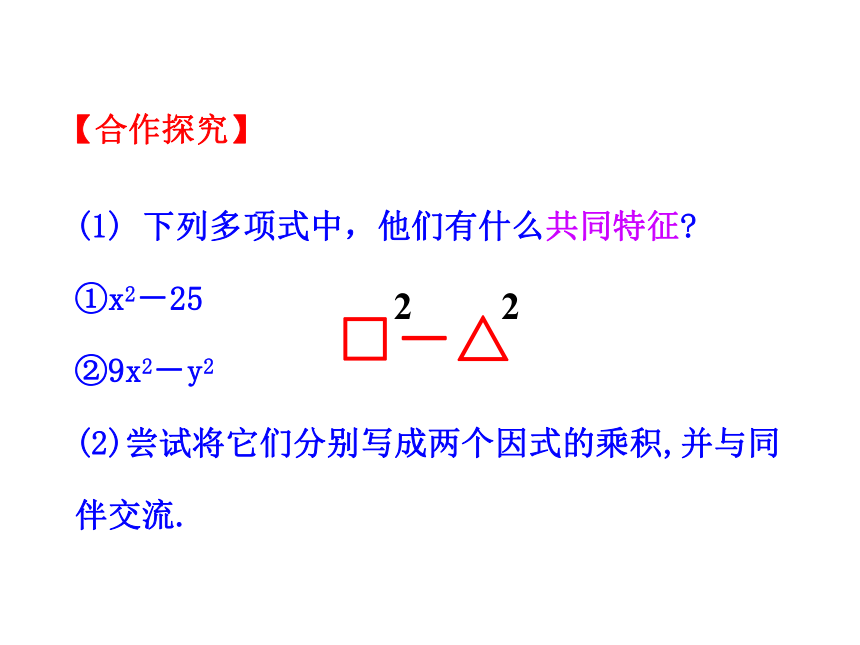
(1) 下列多项式中,他们有什么共同特征
①x2-25
②9x2-y2
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流.
□-△
2
2
【合作探究】
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
【议一议】平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
【结论】形象地表示为:
①左边
②右边
例1 把下列各式因式分解:
(1)25-16x2;
解:(1)原式= 52-(4x)2=(5+4x)(5-4x)
.
【例题】
例2 把下列各式因式分解:
(1)9(m+ n)2-(m-n)2
(2)2x3-8x
解:(1)原式=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)][3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
□-△
2
2
能否化为
首先提取公因式
然后考虑用公式
最终必是乘积式
(2)2x3-8x
=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
在多项式x +y ,x -y ,-x +y ,-x -y 中,能利用
平方差公式分解的有( )
A.1个 B.2个 C.3个 D.4个
B
【想一想】
想一想:以前学过两个乘法公式
把两个公式反过来,就得到
【定义】形如a2+2ab+b2或a2-2ab+b2的式子称为完全平方式.
由因式分解与整式乘法的关系可以看出,如果把乘法公式反过来,那么就可以用来把某些多项式因式分解,这种因式分解的方法叫做公式法.
例3 把以下三个多项式因式分解:
(x+6)2
(x-y)2
(a+b-3)2
【例题】
因式分解:
3a(m+n)2
-(a-2b)2
【做一做】
下列因式分解是否正确?为什么?如果不正确,请给出正确的结果.
不正确,分解不彻底
(y2 + x2 )2 - 4x2y2
你能彻底分解下面的因式吗?
要分解到不能再分解为止.
(x+y)2(x-y)2
【合作探究】
正确结果为(x2+4y2)(x+2y)(x-2y)
1.下列因式分解中,错误的是( )
A.1-9x2=(1+3x)(1-3x)
B.a2-4a+4 =(a-2)2
C.-mx+my=-m(x+y)
D.ax-ay-bx+by=(a-b)(x-y)
【解析】选C.-mx+my=-m(x-y).
2.(江西·中考)因式分解2a2-8=________.
【解析】原式=2(a2-4)=2(a+2)(a-2).
答案:2(a+2)(a-2)
3.一个长方形的面积是(x2-9)平方米,其长为(x+3)米,用含有x的整式表示它的宽为______米.
【解析】因为x2-9=(x+3)(x-3),而其长为(x+3)米,所以由长方形的面积公式得其宽为(x-3)米.
答案:(x-3)
4. 把下列各式因式分解:
(1)36(x+y)2-49(x-y)2;
(2)y3-4y2+4y.
【解析】(1)36(x+y)2-49(x-y)2
=[6(x+y)]2-[7(x-y)]2
=[6(x+y)+7(x-y)][6(x+y)-7(x-y)]
=(6x+6y+7x-7y)(6x+6y-7x+7y)
=(13x-y)(13y-x);
(2)y3-4y2+4y=y(y2-4y+4)= y(y-2)2.
5. 利用简便方法计算:
(1)123×0.24-12.3×0.4-20×1.23;
(2)1.992-2.992;
(3)2082-208×16+64.
【解析】(1)原式=123×0.24-123×0.04-123×0.2
=123×(0.24-0.04-0.2)=123×0=0;
(2)原式=(1.99+2.99)(1.99-2.99)
=4.98×(-1)=-4.98;
(3)原式=2082-2×208×8+82=(208-8)2=40 000.
本课时我们学习了用平方差公式和完全平方公式因式分解.
1.熟记公式的特点是关键.
2.注意当已知完全平方公式的平方项求中间项时,有正负两种情况.
3.若多项式中有公因式时,应先提取公因式,再因式分解.
每个人都应该知道,把语言化为行动,比把行动化为语言困难得多。
——高尔基
3 公式法
1.使学生了解运用公式法因式分解的意义.
2.使学生掌握运用平方差公式因式分解.
3.使学生会用完全平方公式因式分解,进一步发展符号感和推理能力.
一 看系数 二 看字母 三 看指数
最大公约数
相同字母 相同字母的最低次幂
1.把下列各式因式分解:
(1)3a3b2-12ab3
(2)x(a+b)+y(a+b)
(3)a(m-2)+b(2-m)
(4)a(x-y)2-b(y-x)2
【温故知新】
2.填空
(1)25x2 = (_____)2
(2)36a4 = (_____)2
(3)0.49b2 = (_____)2
(4)64x2y2 = (_____)2
(5) = (_____)2
5x
6a2
0.7b
8xy
(1)(x+5)(x-5)=____________
(2)(3x-y)(3x+y)=___________
(3)(1+3a)(1-3a)=___________
(整式乘法)
(因式分解)
1-9a2
x2-25
9x2-y2
(1) 下列多项式中,他们有什么共同特征
①x2-25
②9x2-y2
(2)尝试将它们分别写成两个因式的乘积,并与同伴交流.
□-△
2
2
【合作探究】
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
【议一议】平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
【结论】形象地表示为:
①左边
②右边
例1 把下列各式因式分解:
(1)25-16x2;
解:(1)原式= 52-(4x)2=(5+4x)(5-4x)
.
【例题】
例2 把下列各式因式分解:
(1)9(m+ n)2-(m-n)2
(2)2x3-8x
解:(1)原式=[3(m+n)]2-(m-n)2
=[3(m+n)+(m-n)][3(m+n)-(m-n)]
=(3m+3n+m-n)(3m+3n-m+n)
=(4m+2n)(2m+4n)
=4(2m+n)(m+2n)
□-△
2
2
能否化为
首先提取公因式
然后考虑用公式
最终必是乘积式
(2)2x3-8x
=2x(x2-4)
=2x(x2-22)
=2x(x+2)(x-2)
在多项式x +y ,x -y ,-x +y ,-x -y 中,能利用
平方差公式分解的有( )
A.1个 B.2个 C.3个 D.4个
B
【想一想】
想一想:以前学过两个乘法公式
把两个公式反过来,就得到
【定义】形如a2+2ab+b2或a2-2ab+b2的式子称为完全平方式.
由因式分解与整式乘法的关系可以看出,如果把乘法公式反过来,那么就可以用来把某些多项式因式分解,这种因式分解的方法叫做公式法.
例3 把以下三个多项式因式分解:
(x+6)2
(x-y)2
(a+b-3)2
【例题】
因式分解:
3a(m+n)2
-(a-2b)2
【做一做】
下列因式分解是否正确?为什么?如果不正确,请给出正确的结果.
不正确,分解不彻底
(y2 + x2 )2 - 4x2y2
你能彻底分解下面的因式吗?
要分解到不能再分解为止.
(x+y)2(x-y)2
【合作探究】
正确结果为(x2+4y2)(x+2y)(x-2y)
1.下列因式分解中,错误的是( )
A.1-9x2=(1+3x)(1-3x)
B.a2-4a+4 =(a-2)2
C.-mx+my=-m(x+y)
D.ax-ay-bx+by=(a-b)(x-y)
【解析】选C.-mx+my=-m(x-y).
2.(江西·中考)因式分解2a2-8=________.
【解析】原式=2(a2-4)=2(a+2)(a-2).
答案:2(a+2)(a-2)
3.一个长方形的面积是(x2-9)平方米,其长为(x+3)米,用含有x的整式表示它的宽为______米.
【解析】因为x2-9=(x+3)(x-3),而其长为(x+3)米,所以由长方形的面积公式得其宽为(x-3)米.
答案:(x-3)
4. 把下列各式因式分解:
(1)36(x+y)2-49(x-y)2;
(2)y3-4y2+4y.
【解析】(1)36(x+y)2-49(x-y)2
=[6(x+y)]2-[7(x-y)]2
=[6(x+y)+7(x-y)][6(x+y)-7(x-y)]
=(6x+6y+7x-7y)(6x+6y-7x+7y)
=(13x-y)(13y-x);
(2)y3-4y2+4y=y(y2-4y+4)= y(y-2)2.
5. 利用简便方法计算:
(1)123×0.24-12.3×0.4-20×1.23;
(2)1.992-2.992;
(3)2082-208×16+64.
【解析】(1)原式=123×0.24-123×0.04-123×0.2
=123×(0.24-0.04-0.2)=123×0=0;
(2)原式=(1.99+2.99)(1.99-2.99)
=4.98×(-1)=-4.98;
(3)原式=2082-2×208×8+82=(208-8)2=40 000.
本课时我们学习了用平方差公式和完全平方公式因式分解.
1.熟记公式的特点是关键.
2.注意当已知完全平方公式的平方项求中间项时,有正负两种情况.
3.若多项式中有公因式时,应先提取公因式,再因式分解.
每个人都应该知道,把语言化为行动,比把行动化为语言困难得多。
——高尔基
