初中数学北师大版八年级下册 4.1因式分解 教学评一体化教案
文档属性
| 名称 | 初中数学北师大版八年级下册 4.1因式分解 教学评一体化教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 87.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 00:00:00 | ||
图片预览

文档简介
4.1因式分解 教学评一体化教案
【课标要求】
1.理解因式分解的意义以及因式分解与整式乘法的关系.
2.对因式分解作出正确判断,培养观察能力.
【学习目标】
1.解掌握因式分解的意义,会判断一个变形是否为因式分解.(重点)
2.理解因式分解与整式乘法之间的联系与区别.(难点)
3.对因式分解及整式乘法关系的理解
【评价任务】
1.任务一:合作完成: (指向目标1);独立完成1(检测目标1)
2.任务二:合作完成:(指向目标2);独立完成2(检测目标2)
3.任务三:合作完成:(指向目标3); 独立完成:3(检测目标3)
【资源与建议】
本节学习的因式分解知识是项式因式分解中最基本的知识和最基本的方法,受认知水平和思维水平的限制,仍会有较多的学生不适应,教材充分考虑了这一点,内容梯度小,知识点少且浅,利于学生的学习
2.本主题的重点是经历探索分解因式的过程,体会数学知识之间的整体(整式乘法与因式分解)联系
【学习过程】
先行组织
1. 问题1:24能被哪些数整除?
2.问题2:你是怎样想到的?
3. 思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
任务一:确定公因式---公因式要提尽.(指向目标1)
1.合作探究:因式分解的概念
问题1:993-99能被100整除这个吗?
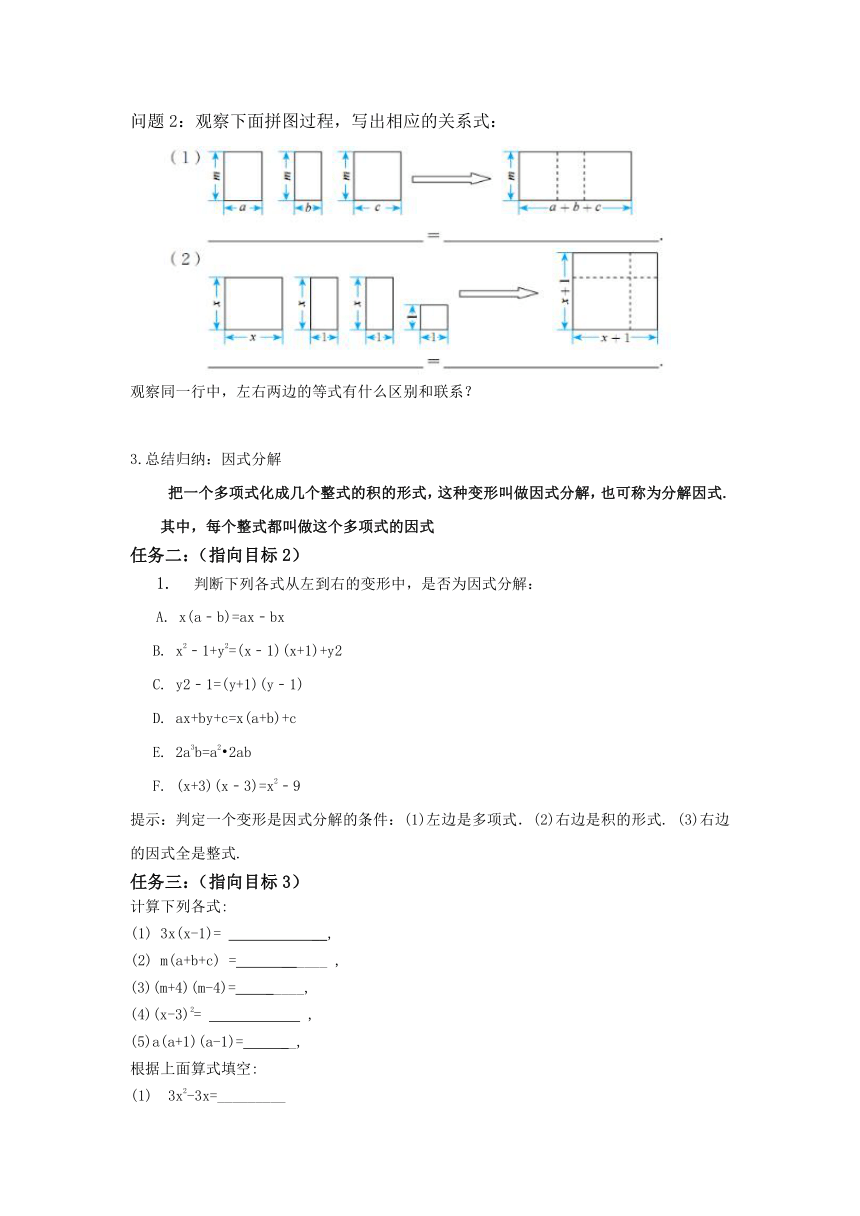
问题2:观察下面拼图过程,写出相应的关系式:
观察同一行中,左右两边的等式有什么区别和联系?
3.总结归纳:因式分解
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解,也可称为分解因式.
其中,每个整式都叫做这个多项式的因式
任务二:(指向目标2)
1. 判断下列各式从左到右的变形中,是否为因式分解:
A. x(a﹣b)=ax﹣bx
B. x2﹣1+y2=(x﹣1)(x+1)+y2
C. y2﹣1=(y+1)(y﹣1)
D. ax+by+c=x(a+b)+c
E. 2a3b=a2 2ab
F. (x+3)(x﹣3)=x2﹣9
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式. (3)右边的因式全是整式.
任务三:(指向目标3)
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
根据上面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
因式分解与整式乘法的关系
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
【达标检测】
1. 下列各式中从左到右的变形属于分解因式的是( )
A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
2. 下列从左到右的变形中,是因式分解的有______ .
①24x2y=4x 6xy ②(x+5)(x﹣5)=x2﹣25 ③x2+2x﹣3=(x+3)(x﹣1)
④9x2﹣6x+1=3x(x﹣2)+1 ⑤x2+1=x(x+ )⑥3xn+2+27xn=3xn( x2+9)
3. 把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
4. 20042+2004能被2005整除吗
5. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),求a+b的值.
【学后反思】
完善思维导图,梳理本节课学习的知识内容和数学思想方法:
评价任务自我量化表
评价任务 得分 总得分 等级 评价标准
评价任务1 本课时评价任务总分共40分 A级:达到总分的80%(32分)及以上; B级:达到总分的70%(28分)及以上; C级:达到总分的60%(24分)及以上; D级:达到总分的60%(24分)以下.
评价任务2
评价任务3
达标检测
【学习提示】 对本节的学习进行归纳形成知识框架,并从学习经历中反思学会了什么,存在什么问题及掌握了那些解决数学问题的方法.
【分层作业】
一、基础巩固题(指向全体学生)
1.下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
二、能力提升题(指向等级为A和B的学生)
1. 若多项式x2+ax+b分解因式的结果为a(x﹣2)(x+3),求a,b的值.
【课标要求】
1.理解因式分解的意义以及因式分解与整式乘法的关系.
2.对因式分解作出正确判断,培养观察能力.
【学习目标】
1.解掌握因式分解的意义,会判断一个变形是否为因式分解.(重点)
2.理解因式分解与整式乘法之间的联系与区别.(难点)
3.对因式分解及整式乘法关系的理解
【评价任务】
1.任务一:合作完成: (指向目标1);独立完成1(检测目标1)
2.任务二:合作完成:(指向目标2);独立完成2(检测目标2)
3.任务三:合作完成:(指向目标3); 独立完成:3(检测目标3)
【资源与建议】
本节学习的因式分解知识是项式因式分解中最基本的知识和最基本的方法,受认知水平和思维水平的限制,仍会有较多的学生不适应,教材充分考虑了这一点,内容梯度小,知识点少且浅,利于学生的学习
2.本主题的重点是经历探索分解因式的过程,体会数学知识之间的整体(整式乘法与因式分解)联系
【学习过程】
先行组织
1. 问题1:24能被哪些数整除?
2.问题2:你是怎样想到的?
3. 思考:既然有些数能分解因数,那么类似地,有些多项式可以分解成几个整式的积吗?
任务一:确定公因式---公因式要提尽.(指向目标1)
1.合作探究:因式分解的概念
问题1:993-99能被100整除这个吗?
问题2:观察下面拼图过程,写出相应的关系式:
观察同一行中,左右两边的等式有什么区别和联系?
3.总结归纳:因式分解
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解,也可称为分解因式.
其中,每个整式都叫做这个多项式的因式
任务二:(指向目标2)
1. 判断下列各式从左到右的变形中,是否为因式分解:
A. x(a﹣b)=ax﹣bx
B. x2﹣1+y2=(x﹣1)(x+1)+y2
C. y2﹣1=(y+1)(y﹣1)
D. ax+by+c=x(a+b)+c
E. 2a3b=a2 2ab
F. (x+3)(x﹣3)=x2﹣9
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式. (3)右边的因式全是整式.
任务三:(指向目标3)
计算下列各式:
(1) 3x(x-1)= __,
(2) m(a+b+c) = ______ ,
(3)(m+4)(m-4)= _____,
(4)(x-3)2= ,
(5)a(a+1)(a-1)= __,
根据上面算式填空:
(1) 3x2-3x=_________
(2)ma+mb+mc=___________
(3) m2-16=__________
(4) x2-6x+9=________
(5) a3-a=___________
因式分解与整式乘法的关系
想一想:由a(a+1)(a-1)得到a3-a的变形是什么运算
由a3-a得到a(a+1)(a-1)的变形与它有什么不同
由a(a+1)(a-1)得到a3-a的变形是整式乘法,
由a3-a得到a(a+1)(a-1)的变形与上面的变形互为逆过程.
【达标检测】
1. 下列各式中从左到右的变形属于分解因式的是( )
A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2
C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ )
2. 下列从左到右的变形中,是因式分解的有______ .
①24x2y=4x 6xy ②(x+5)(x﹣5)=x2﹣25 ③x2+2x﹣3=(x+3)(x﹣1)
④9x2﹣6x+1=3x(x﹣2)+1 ⑤x2+1=x(x+ )⑥3xn+2+27xn=3xn( x2+9)
3. 把多项式x2+4mx+5因式分解得(x+5)(x+n),则m+n的值为 .
4. 20042+2004能被2005整除吗
5. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),求a+b的值.
【学后反思】
完善思维导图,梳理本节课学习的知识内容和数学思想方法:
评价任务自我量化表
评价任务 得分 总得分 等级 评价标准
评价任务1 本课时评价任务总分共40分 A级:达到总分的80%(32分)及以上; B级:达到总分的70%(28分)及以上; C级:达到总分的60%(24分)及以上; D级:达到总分的60%(24分)以下.
评价任务2
评价任务3
达标检测
【学习提示】 对本节的学习进行归纳形成知识框架,并从学习经历中反思学会了什么,存在什么问题及掌握了那些解决数学问题的方法.
【分层作业】
一、基础巩固题(指向全体学生)
1.下列多项式中,分解因式的结果为-(x+y)(x-y)的是( )
A.x2﹣y2 B.﹣x2+y2
C.x2+y2 D.﹣x2﹣y2
二、能力提升题(指向等级为A和B的学生)
1. 若多项式x2+ax+b分解因式的结果为a(x﹣2)(x+3),求a,b的值.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
