四川省成都市简阳实验学校(成都石室阳安学校)2023-2024学年高二下学期期中考试数学试题(PDF版,无答案)
文档属性
| 名称 | 四川省成都市简阳实验学校(成都石室阳安学校)2023-2024学年高二下学期期中考试数学试题(PDF版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 246.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-30 00:00:00 | ||
图片预览

文档简介
成都石室阳安学校高 2022级高二(下)半期考试数学试题
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只
有一项是符合题目要求.
1.已知等差数列 an 的前 n项和为 Sn,a5 a7 14,则 S11 ( )
A.140 B.70 C.154 D.77
x2 y22.椭圆 2 2 1(a b 0)的左、右顶点分别是 A,B,椭圆的左焦点和中心分别是 F ,O.已知 FOa b
是 AF , FB 的等比中项,则此椭圆的离心率为( )
A 1
1
. 5 2 B 2 . C.
2 2
D.
4
3.在数列 an 中,已知 a1 1,a2 1,且 an an 1 3an 2 2( n 3),则 a4 ( )
A.13 B.9 C.11 D.7
5.函数 f x lnx图象上的点到直线 y x的距离的最小值是( )
ln2
A. B 2. C.1 D.
2 22
6.已知函数 f x 满足 f x f 2 ex 2 1 f 0 x x2,则 f x 的单调递增区间为( )
2
A. ,0 B. 1, C. ,1 D. 0,
8.在数列 an 3中,Sn为其前 n项和,首项 a1 1,又函数 f x x an 1 sin x 2an 1 x 1,若
f 0 0,则 S2024 ( )
A. 22023 2024 B. 22024 2025 C. 22025 2026 D. 22026 2027
第 1 页 共 4 页
{#{QQABCYACEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
二、多选题(本题 3题,每题 6分,共 18分,全部选对得 6分,部分选对得部分分,
有选错得 0分)
9.已知数列 an *是等差数列,数列 bn 是等比数列 n N ,则下列说法正确的是( )
A.若 p,q为实数,则 pan qbn 是等比数列
B.若数列 an 的前 n项和为 Sn,则 S5, S10 S5 , S15 S10 成等差数列
C.若数列 bn 的公比 q 1,则数列 bn 是递增数列
D.若数列 an 的公差 d 0,则数列 an 是递减数列
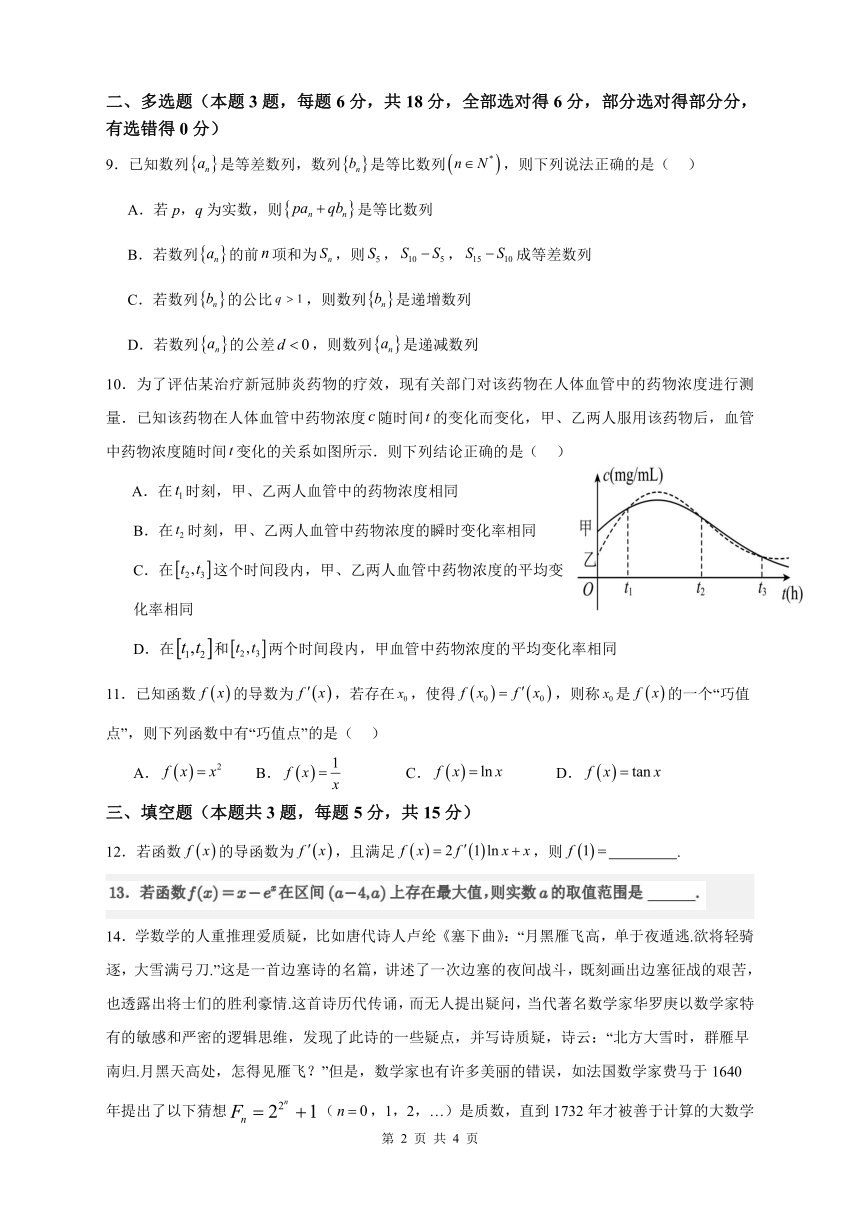
10.为了评估某治疗新冠肺炎药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测
量.已知该药物在人体血管中药物浓度 c随时间 t的变化而变化,甲、乙两人服用该药物后,血管
中药物浓度随时间 t变化的关系如图所示.则下列结论正确的是( )
A.在 t1时刻,甲、乙两人血管中的药物浓度相同
B.在 t2 时刻,甲、乙两人血管中药物浓度的瞬时变化率相同
C.在 t2 , t3 这个时间段内,甲、乙两人血管中药物浓度的平均变
化率相同
D.在 t1,t2 和 t2 , t3 两个时间段内,甲血管中药物浓度的平均变化率相同
11.已知函数 f x 的导数为 f x ,若存在 x0,使得 f x0 f x0 ,则称 x0是 f x 的一个“巧值
点”,则下列函数中有“巧值点”的是( )
A. f x x2 1B. f x C. f x ln x D. f x tan x
x
三、填空题(本题共 3题,每题 5分,共 15分)
12.若函数 f x 的导函数为 f x ,且满足 f x 2 f 1 ln x x,则 f 1 .
14.学数学的人重推理爱质疑,比如唐代诗人卢纶《塞下曲》:“月黑雁飞高,单于夜遁逃.欲将轻骑
逐,大雪满弓刀.”这是一首边塞诗的名篇,讲述了一次边塞的夜间战斗,既刻画出边塞征战的艰苦,
也透露出将士们的胜利豪情.这首诗历代传诵,而无人提出疑问,当代著名数学家华罗庚以数学家特
有的敏感和严密的逻辑思维,发现了此诗的一些疑点,并写诗质疑,诗云:“北方大雪时,群雁早
南归.月黑天高处,怎得见雁飞?”但是,数学家也有许多美丽的错误,如法国数学家费马于 1640
n
年提出了以下猜想 Fn 2
2 1( n 0,1,2,…)是质数,直到 1732年才被善于计算的大数学
第 2 页 共 4 页
{#{QQABCYCAEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
1
家欧拉算出F5 641*6700417,不是质数.现设 an log2 log2 Fn 1 ( n 1,2,…),bn an an 1 ,
则数列 bn 的前 n项和 Sn .
四、解答题(本题共 5题,共 77分,解答应写出文字说明、证明过程或演算步骤。)
15 2.(本小题满分 13分)已知函数 f x x x 3lnx .
(1)求曲线 y f x 在点 1, f 1 处的切线方程;
(2)求 f x 的极值.
16.(本小题满分 15分)已知等差数列 an 中的前 n项和为 Sn,且 a2,a5,a14成等比数列,S5 25.
(1)求数列 an 的通项公式;
(2) n若数列 an 为递增数列,记bn 2 an,求数列 bn 的前 n项的和Tn.
17.(本小题满分 15分)如图,AE 平面 ABCD,CF∥ AE, AD∥BC,
AD AB, AB AD 1, AE BC 2 .
(Ⅰ)求证: BF∥平面 ADE;
(Ⅱ)求直线CE与平面BDE所成角的正弦值;
第 3 页 共 4 页
{#{QQABCYCAEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
18 x.(本小题满分 17分)已知函数 f x e ax .
(1)讨论函数 f x 的单调区间;
(2)当 x 2时, f x 0恒成立,求 a的取值范围.
2
19 17 x y
2
.(本小题满分 分)已知椭圆 2 2 1 a b 0 右焦点 F 1,0
2
,离心率为 ,过 F 作两条
a b 2
互相垂直的弦 AB,CD,设 AB,CD中点分别为M ,N .
(1)求椭圆的标准方程;
(2)证明:直线MN必过定点,并求出此定点坐标.
第 4 页 共 4 页
{#{QQABCYACEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只
有一项是符合题目要求.
1.已知等差数列 an 的前 n项和为 Sn,a5 a7 14,则 S11 ( )
A.140 B.70 C.154 D.77
x2 y22.椭圆 2 2 1(a b 0)的左、右顶点分别是 A,B,椭圆的左焦点和中心分别是 F ,O.已知 FOa b
是 AF , FB 的等比中项,则此椭圆的离心率为( )
A 1
1
. 5 2 B 2 . C.
2 2
D.
4
3.在数列 an 中,已知 a1 1,a2 1,且 an an 1 3an 2 2( n 3),则 a4 ( )
A.13 B.9 C.11 D.7
5.函数 f x lnx图象上的点到直线 y x的距离的最小值是( )
ln2
A. B 2. C.1 D.
2 22
6.已知函数 f x 满足 f x f 2 ex 2 1 f 0 x x2,则 f x 的单调递增区间为( )
2
A. ,0 B. 1, C. ,1 D. 0,
8.在数列 an 3中,Sn为其前 n项和,首项 a1 1,又函数 f x x an 1 sin x 2an 1 x 1,若
f 0 0,则 S2024 ( )
A. 22023 2024 B. 22024 2025 C. 22025 2026 D. 22026 2027
第 1 页 共 4 页
{#{QQABCYACEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
二、多选题(本题 3题,每题 6分,共 18分,全部选对得 6分,部分选对得部分分,
有选错得 0分)
9.已知数列 an *是等差数列,数列 bn 是等比数列 n N ,则下列说法正确的是( )
A.若 p,q为实数,则 pan qbn 是等比数列
B.若数列 an 的前 n项和为 Sn,则 S5, S10 S5 , S15 S10 成等差数列
C.若数列 bn 的公比 q 1,则数列 bn 是递增数列
D.若数列 an 的公差 d 0,则数列 an 是递减数列
10.为了评估某治疗新冠肺炎药物的疗效,现有关部门对该药物在人体血管中的药物浓度进行测
量.已知该药物在人体血管中药物浓度 c随时间 t的变化而变化,甲、乙两人服用该药物后,血管
中药物浓度随时间 t变化的关系如图所示.则下列结论正确的是( )
A.在 t1时刻,甲、乙两人血管中的药物浓度相同
B.在 t2 时刻,甲、乙两人血管中药物浓度的瞬时变化率相同
C.在 t2 , t3 这个时间段内,甲、乙两人血管中药物浓度的平均变
化率相同
D.在 t1,t2 和 t2 , t3 两个时间段内,甲血管中药物浓度的平均变化率相同
11.已知函数 f x 的导数为 f x ,若存在 x0,使得 f x0 f x0 ,则称 x0是 f x 的一个“巧值
点”,则下列函数中有“巧值点”的是( )
A. f x x2 1B. f x C. f x ln x D. f x tan x
x
三、填空题(本题共 3题,每题 5分,共 15分)
12.若函数 f x 的导函数为 f x ,且满足 f x 2 f 1 ln x x,则 f 1 .
14.学数学的人重推理爱质疑,比如唐代诗人卢纶《塞下曲》:“月黑雁飞高,单于夜遁逃.欲将轻骑
逐,大雪满弓刀.”这是一首边塞诗的名篇,讲述了一次边塞的夜间战斗,既刻画出边塞征战的艰苦,
也透露出将士们的胜利豪情.这首诗历代传诵,而无人提出疑问,当代著名数学家华罗庚以数学家特
有的敏感和严密的逻辑思维,发现了此诗的一些疑点,并写诗质疑,诗云:“北方大雪时,群雁早
南归.月黑天高处,怎得见雁飞?”但是,数学家也有许多美丽的错误,如法国数学家费马于 1640
n
年提出了以下猜想 Fn 2
2 1( n 0,1,2,…)是质数,直到 1732年才被善于计算的大数学
第 2 页 共 4 页
{#{QQABCYCAEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
1
家欧拉算出F5 641*6700417,不是质数.现设 an log2 log2 Fn 1 ( n 1,2,…),bn an an 1 ,
则数列 bn 的前 n项和 Sn .
四、解答题(本题共 5题,共 77分,解答应写出文字说明、证明过程或演算步骤。)
15 2.(本小题满分 13分)已知函数 f x x x 3lnx .
(1)求曲线 y f x 在点 1, f 1 处的切线方程;
(2)求 f x 的极值.
16.(本小题满分 15分)已知等差数列 an 中的前 n项和为 Sn,且 a2,a5,a14成等比数列,S5 25.
(1)求数列 an 的通项公式;
(2) n若数列 an 为递增数列,记bn 2 an,求数列 bn 的前 n项的和Tn.
17.(本小题满分 15分)如图,AE 平面 ABCD,CF∥ AE, AD∥BC,
AD AB, AB AD 1, AE BC 2 .
(Ⅰ)求证: BF∥平面 ADE;
(Ⅱ)求直线CE与平面BDE所成角的正弦值;
第 3 页 共 4 页
{#{QQABCYCAEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
18 x.(本小题满分 17分)已知函数 f x e ax .
(1)讨论函数 f x 的单调区间;
(2)当 x 2时, f x 0恒成立,求 a的取值范围.
2
19 17 x y
2
.(本小题满分 分)已知椭圆 2 2 1 a b 0 右焦点 F 1,0
2
,离心率为 ,过 F 作两条
a b 2
互相垂直的弦 AB,CD,设 AB,CD中点分别为M ,N .
(1)求椭圆的标准方程;
(2)证明:直线MN必过定点,并求出此定点坐标.
第 4 页 共 4 页
{#{QQABCYACEgxggiiQAkAJJbIAACRJ5gKCFEQXwCUEqGQQkkJBEEhALACoAMoORRgBAAJOEMAYAiIiAJFSIQBFKAB=C}#A} =}#}
同课章节目录
