2024年初中科学重点题型复习-浮力计算题(含解析)
文档属性
| 名称 | 2024年初中科学重点题型复习-浮力计算题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 836.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2024-04-30 08:01:52 | ||
图片预览



文档简介
2024年初中科学重点题型复习-浮力计算题
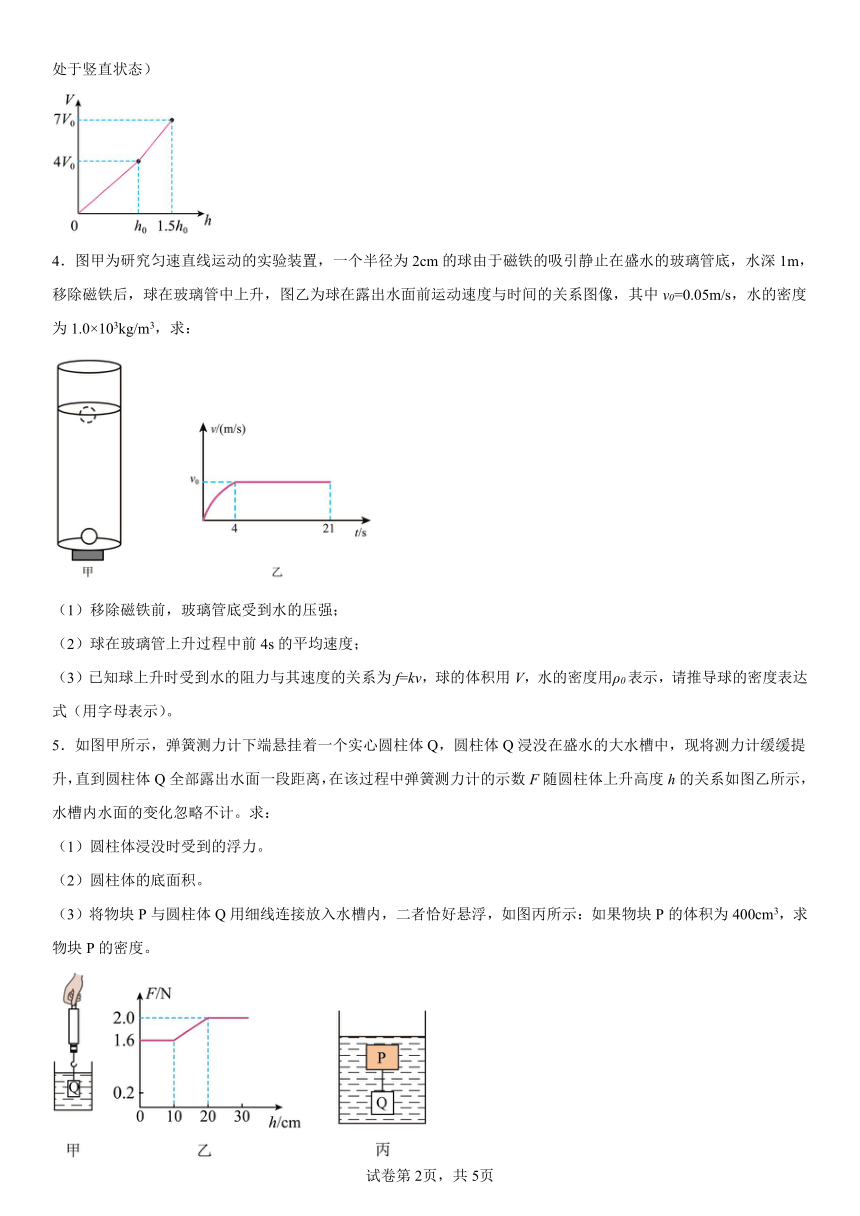
1.如图所示,两个完全相同的底面积为100cm2的轻质薄壁圆柱形容器A、B放在水平桌面上(容器足够高),另有两个完全相同的圆柱体甲、乙,其底面积为50cm2。A中盛有质量为5kg的水,B中放置圆柱体乙,(g取10N/kg)求:
(1)容器A中水的重力;
(2)水对容器A底部的压强p;
(3)若通过两种方法分别增大容器对水平桌面的压强和液体对容器底部的压强,并测出容器对水平桌面的压强变化量 p容、水对容器底部的压强变化量 p水,如下表所示。
方法 容器对水平桌面的压强变化量 p容(帕) 水对容器底部的压强变化量 p水(帕)
① 6000 3000
② 5000 8000
方法a:圆柱体甲放入盛有水的容器A中。
方法b:向放置圆柱体乙的容器B加入质量为5千克的水。
请根据表中的信息,通过计算判断方法a、b与表中方法①、②的对应关系,并求圆柱体甲、乙的密度。
2.如图所示,水平地面上有一底面积为1.5×10-2m2的圆柱形容器。容器中水深40cm,一个边长为10cm的正方体物块通过一根细线与容器底部相连,细线受到的拉力为4N。求:
(1)此时容器底受到水的压强和压力;
(2)此时物块受到的浮力;
(3)细线剪断后,物块静止时浸入水中的体积。
3.有两个不吸水的圆柱体A和圆柱体B,A的顶部系有一根轻质细线。已知A的质量为1.32kg,密度为1.1×103kg/m3,高为12cm,B的底面积为40cm2,求:
(1)A的底面积为多少cm2;
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,求A对B的压强;
(3)将A竖直放入薄壁柱形容器中,向容器中缓慢加入液体直至加满。液体体积与深度的关系如图所示。然后用细线将A竖直向上提升3cm,细线的拉力为6.3N,液体对容器底部的压力减小,求该液体的密度。(圆柱体A始终处于竖直状态)
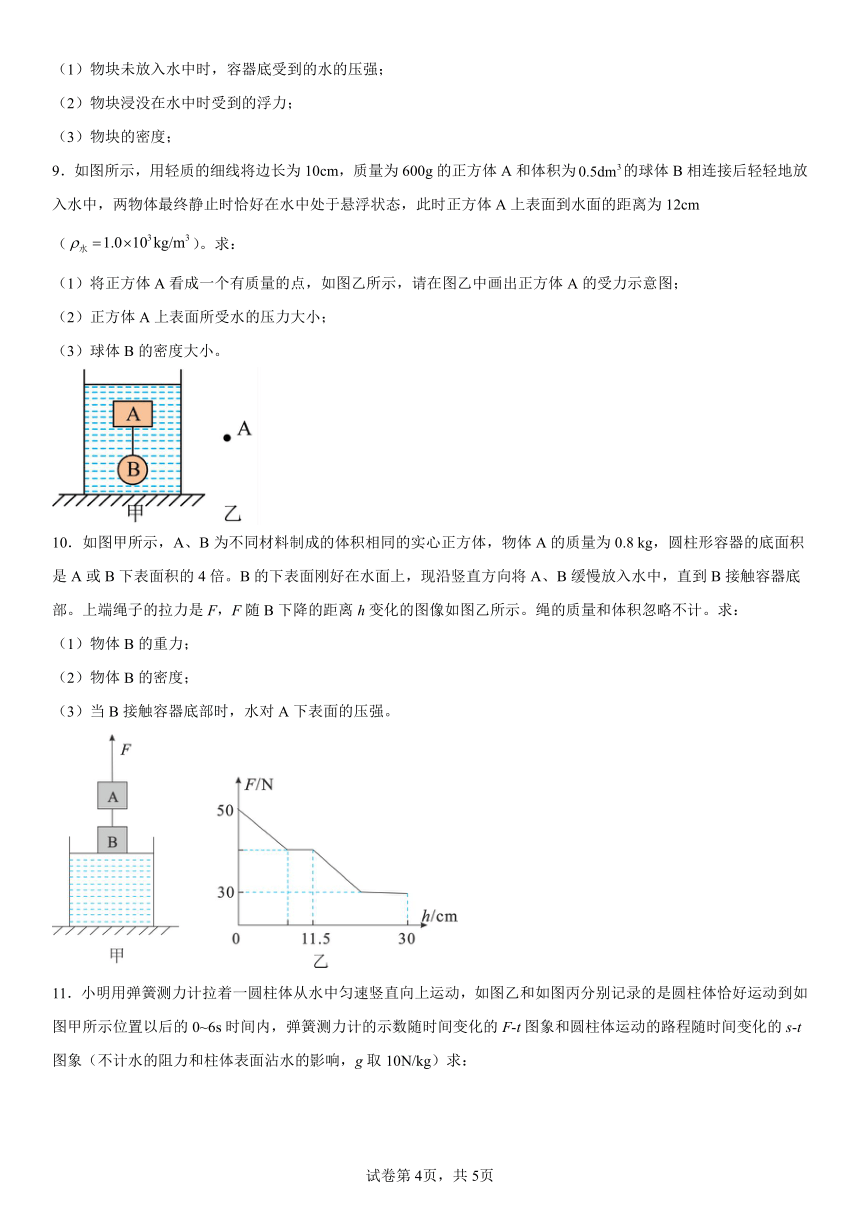
4.图甲为研究匀速直线运动的实验装置,一个半径为2cm的球由于磁铁的吸引静止在盛水的玻璃管底,水深1m,移除磁铁后,球在玻璃管中上升,图乙为球在露出水面前运动速度与时间的关系图像,其中v0=0.05m/s,水的密度为1.0×103kg/m3,求:
(1)移除磁铁前,玻璃管底受到水的压强;
(2)球在玻璃管上升过程中前4s的平均速度;
(3)已知球上升时受到水的阻力与其速度的关系为f=kv,球的体积用V,水的密度用ρ0表示,请推导球的密度表达式(用字母表示)。
5.如图甲所示,弹簧测力计下端悬挂着一个实心圆柱体Q,圆柱体Q浸没在盛水的大水槽中,现将测力计缓缓提升,直到圆柱体Q全部露出水面一段距离,在该过程中弹簧测力计的示数F随圆柱体上升高度h的关系如图乙所示,水槽内水面的变化忽略不计。求:
(1)圆柱体浸没时受到的浮力。
(2)圆柱体的底面积。
(3)将物块P与圆柱体Q用细线连接放入水槽内,二者恰好悬浮,如图丙所示:如果物块P的体积为400cm3,求物块P的密度。
6.小虎同学研究弹簧测力计的示数F与金属块A下表面离液面的距离h的关系,实验装置如图甲所示。用弹簧测力计提着金属块A,使其缓慢浸入酒精中(ρ酒精=0.8×103kg/m3且液体未溢出,g=10N/kg),得到F与h的关系图象如图乙所示。请计算:
(1)金属块A完全浸没在液体受到的浮力;
(2)金属块A的密度;
(3)金属块A的底面积。
7.2022年5月15日凌晨1点26分,中国自主研发的“极目一号”III型浮空艇从海拔4270m的科考营地顺利升空,如图甲所示,4点40分达到9032m,超过珠峰8848.86m的高度,创造浮空艇大气科学观测世界纪录。已知浮空艇体积约为9000m3,总质量约为2.6t。求:
(1)浮空艇受到的重力;
(2)已知科考营地的空气密度约为0.8kg/m3,此时浮空艇受到的浮力;
(3)为了有效控制浮空艇,用缆绳将其系在一辆质量为90t的锚泊车上,如图乙所示。浮空艇未升空时,缆绳处于竖直拉直状态且重力忽略不计,锚泊车对地面的压力。
8.放在水平桌面上的薄壁圆柱形容器重8N,底面积0.01 m2,弹簧测力计的挂钩上挂着一物块,现将物块从水面上方以恒定的速度下降,直至全部没入水中,容器内水的 深度由16cm升高到20cm,如图甲所示,图乙是绳子的拉力随时间t变化的图象,若不 计水的阻力(ρ水=1.0×103kg/m3),(g取 10N/kg)求:
(1)物块未放入水中时,容器底受到的水的压强;
(2)物块浸没在水中时受到的浮力;
(3)物块的密度;
9.如图所示,用轻质的细线将边长为10cm,质量为600g的正方体A和体积为的球体B相连接后轻轻地放入水中,两物体最终静止时恰好在水中处于悬浮状态,此时正方体A上表面到水面的距离为12cm()。求:
(1)将正方体A看成一个有质量的点,如图乙所示,请在图乙中画出正方体A的受力示意图;
(2)正方体A上表面所受水的压力大小;
(3)球体B的密度大小。
10.如图甲所示,A、B为不同材料制成的体积相同的实心正方体,物体A的质量为0.8 kg,圆柱形容器的底面积是A或B下表面积的4倍。B的下表面刚好在水面上,现沿竖直方向将A、B缓慢放入水中,直到B接触容器底部。上端绳子的拉力是F,F随B下降的距离h变化的图像如图乙所示。绳的质量和体积忽略不计。求:
(1)物体B的重力;
(2)物体B的密度;
(3)当B接触容器底部时,水对A下表面的压强。
11.小明用弹簧测力计拉着一圆柱体从水中匀速竖直向上运动,如图乙和如图丙分别记录的是圆柱体恰好运动到如图甲所示位置以后的0~6s时间内,弹簧测力计的示数随时间变化的F-t图象和圆柱体运动的路程随时间变化的s-t图象(不计水的阻力和柱体表面沾水的影响,g取10N/kg)求:
(1)圆柱体浸没在水中时受到的浮力大小;
(2)圆柱体的体积;
(3)圆柱体的密度;
(4)圆柱体竖直放置在水平桌面时对桌面的压强。
12.如图所示,一边长为,密度为的正方体木块,将它用细线系于某容器的水中,()。求:
(1)木块所受的浮力;
(2)细线的拉力;
(3)剪断细线后,木块静止时排开水的体积。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)50N;(2)5000Pa;(3)方法b与②对应,则方法a与①对应,2×103kg/m3
【详解】解:(1)容器A中水的重力为
(2)水对容器A底部的压力为
水对容器A底部的压强为
(3)方法b:向放置圆柱体乙的容器B加入质量为5kg的水,容器对桌面的压强变化量为
所以,方法b与方法②对应,则方法a与①对应。
方法a:圆柱体甲放入盛有水的容器A中,容器对水平桌面的压力变化量为
则圆柱体的质量为
方法a:圆柱体甲放入盛有水的容器A中,因圆柱体对水的压力和水对圆柱体的浮力是一对相互作用力,所以,圆柱体受到的浮力为
由前面的计算可知,圆柱体的重力为50N,浮力小于重力,故圆柱体沉底,所以,在物体完全浸没时,圆柱体的体积和排开水的体积相等,所以,圆柱体的体积是
圆柱体的密度为
答:(1)容器A中水的重力50N;
(2)水对容器A底部的压强p是5000Pa;
(3)通过计算判断方法b与②对应,则方法a与①对应,圆柱体甲、乙的密度是2×103kg/m3。
2.(1),60N;(2)10N;(3)。
【详解】(1)容器底受到水的压强
水对容器底的压力为
(2)木块的体积
木块浸没在水中时受到的浮力
(3)物体受到竖直向下的重力和拉力、竖直向上的浮力,处于静止状态,则物体的重力为
因为木块浸没在水中时的浮力大于木块的重力,所以剪断细线后,木块会上浮直至漂浮在水面上,由于木块漂浮,木块受到的浮力
由得此时排开水的体积浸入水中的体积
答:(1)此时容器底受到水的压强为4000Pa,压力为60N;
(2)此时物块受到的浮力为10N;
(3)细线剪断后,物块静止时浸入水中的体积为。
3.(1)100;(2)3.3×103Pa;(2)1.4×103kg/cm3
【详解】解:(1)已知物体A的质量和密度
mA=1.32kg,ρA=1.1×103kg/m3
则A的体积
又A的高度
hA=12cm=0.12m
所以A的底面积
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,由于A的底面积大于B的底面积,因此,此时受力面积为
SB=40cm2=4×10-3m2
A对B的压强
(3)结合图像可知
,
故可得
已知SA=100cm2,故容器底面积
S容=3SA=3×100cm2=300cm2
用细线将A竖直向上提升3cm,因为液体对容器底部的压力减小,所以可判断此时液面下降了,说明物体A是漂浮状态,物体A的重力
GA=mAg=1.32kg×10N/kg=13.2N
当细绳拉着物体A向上移动h=3cm后,细线的拉力F=6.3N,则此时物体A的浮力
F浮′=G-F=13.2N-6.3N=6.9N
设液面下降的高度为h,则物体A排开液体的体积变化量
V排=SA(h+h)=S容h
带入已知量可得
V排=1×10-2m2×(h+0.03m)=3×10-2h
解得
h=0.015m,V排=4.5×10-4m3
浮力的变化量
F浮=13.2N-6.9N=6.3N
则液体密度
答:(1)A的底面积为100cm2;
(2)A对B的压强为3.3×103Pa;
(3)该液体的密度为1.4×103kg/cm3。
4.(1)1×104Pa;(2)0.0275m/s;(3)
【详解】解:(1)移除磁铁前,水深h=1m,所以玻璃管底受到水的压强
p=ρgh=1.0×103kg/m3×10N/kg×1m=1×104Pa
(2)由图可知,球在露出水面前运动的时间为21s,根据可得,4~21s球上升的距离
s0=v0t=0.05m/s×17s=0.85m
则球在玻璃管上升过程中前4s上升的距离
s′=s-s0=1m-0.85m-2×0.02m=0.11m
所以球在玻璃管上升过程中前4s的平均速度
(3)由图可知,球4~21s时匀速上升,受力平衡,所以有
G+f=F浮
即
解得球的密度
答:(1)玻璃管底受到水的压强是1×104Pa;
(2)球在玻璃管上升过程中前4s的平均速度0.0275m/s;
(3)球的密度表达式。
5.(1)2.0N;(2)4×10﹣4m2;(3)0.6×103kg/m3
【详解】解:(1)由图乙知,当上升高度在20cm以上,圆柱体脱离水面,弹簧测力计示数F=2.0N,此时圆柱体处于空气中,圆柱体Q的重力为
由图乙知,圆柱体上升高度在0~10cm时,圆柱体Q浸没在水中,根据称重法可知,Q所受到的浮力为
(2)由阿基米德原理可得圆柱体Q的体积为
由图乙知,上升10cm时圆柱体上表面与水面恰相平,上升20cm时圆柱体恰好全部露出水面,所以圆柱体高度为
圆柱体的底面积为
(3)图丙中物块P和与圆柱体Q悬浮在水中,则P、Q排开水的体积为
P、Q所受的总浮力为
根据悬浮体积可知:P、Q的总重力为
则P的重力为
P的质量为
所以P的密度为
答:(1)圆柱体的重力为2.0N;
(2)圆柱体的底面积为4×10﹣4m2;
(3)将物块P与圆柱体Q用细线连接放入装水容器内,二者恰好悬浮如图丙所示。如果物块P的体积为400cm3,则物块P的密度为0.6×103kg/m3。
6.(1)4N;(2)2×103kg/m3;(3)100cm2
【详解】解:(1)由图知,当h1=0时,弹簧测力计的示数为10N,即物体A的重力G=10N,完全浸没在液体中时,排开液体的体积不变,根据阿基米德原理可知,受到的浮力不变,由F浮=G-F可知,测力计示数不变,故由图象可知物体的高度h=5.0cm;A浸没时受到液体的浮力
F浮=G-F=10N-6N=4N
(2)根据阿基米德原理可知物体所受的浮力
F浮=ρ酒精gV排=ρ酒精gV物
金属块A的体积
①
金属块A的密度
②
由①②得:金属块A的密度
(3)金属块A的底面积是
答:(1)金属块A完全浸没在液体受到的浮力为4N;
(2)金属块A的密度为2×103kg/m3;
(3)金属块A的底面积为100cm2。
7.(1)2.6×104N;(2)7.2×104N;(3)8.54×105N
【详解】解:(1)浮空艇受到的重力为
G艇=m艇g=2.6×103kg×10N/kg=2.6×104N
(2)此时浮空艇受到的浮力
F浮=ρ空气gV排=ρ空气gV=0.8kg/m3×10N/kg×9000m3=7.2×104N
(3)浮空艇未升空时,缆绳处于竖直拉直状态,此时浮空艇受到向下的重力和拉力、向上的浮力作用,根据力的平衡条件可知绳子的拉力
F拉=F浮﹣G艇=7.2×104N﹣2.6×104N=4.6×104N
锚泊车的重力为
G车=m车g=90×103kg×10N/kg=9×105N
锚泊车受竖直向下的重力、竖直向上的拉力和支持力作用,则地面对车的支持力为
F支=G车﹣F拉=9×105N﹣4.6×104N=8.54×105N
由于物体间力的作用是相互的,则锚泊车对地面的压力
F压=F支=8.54×105N
答:(1)浮空艇受到的重力为2.6×104N;
(2)此时浮空艇受到的浮力为7.2×104N;
(3)锚泊车对地面的压力为8.54×105N。
8.(1)1600Pa;(2)4N(3)2.5×103kg/m3
【详解】(1).物块未放入水中时,容器底受到的水的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.16m=1600Pa;
(2).物块浸没后,水的深度增加量:
△h=20cm 16cm=4cm=0.04m,
物块浸没在水中时物体排开水的体积:
V排=V物=S△h=0.01m2×0.04m=4×10 4m3,
物块受到的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×4×10 4m3=4N;
(3).由图乙可知,物块的重力G=F=10N,
物块的质量:m== =1kg,
物块的密度:ρ物= ==2.5×103kg/m3
答:(1).物块未放入水中时,容器底受到的水的压强为1600Pa;
(2).物块浸没在水中时受到的浮力为4N;
(3).物块的密度为2.5×103kg/m3;
9.(1) ;(2)12N;(3)
【详解】解:(1)对A进行受力分析A受到竖直向上的浮力,竖直向下的重力和拉力,如图所示:
(2)正方体A上表面所处的深度为
正方体A上表面所受水的压强
接触面积为
正方体A上表面所受水的压力大小为
(3)正方体A的体积为
正方体A和球体B浸入液体的总体积为
因为正方体A和球体B这个整体在水中悬浮,所以总重力等于浮力,故总重力为
A和B的总质量为
球体B的质量为
球体B的密度大小为
答:(1)将正方体A看成一个有质量的点,正方体A的受力示意图为;
(2)正方体A上表面所受水的压力大小为12N;
(3)球体B的密度大小为。
10.(1);(2);(3)
【详解】解:(1)物体A的重力
当h=0时,绳子的拉力大小等于物体A、B的重力之和,由图可知,当h=0时,拉力大小F0=50N,则物体B的重力为
(2)由图可知,绳子的拉力最后变为30N不变,此时物体A、B完全浸没在水中,浮力不变,此时物体A、B所受浮力之和为
物体A、B排开水的体积为
物体A、B的体积相同,所以物体B的体积为
物体B的质量
物体B的密度为
(3)物体A、B的边长为
由图可知,当h=30cm时,B接触容器底部,所以原来烧杯中水的深度为30cm,A、B的底面积为
烧杯的底面积
当A、B完全浸没以后,液面上升的高度为
当A、B完全浸没以后,烧杯中水的深度为
由图可知,当h=11.5cm时,绳子的拉力第二次减小,说明此时物体A开始进入水中,此时只有B浸没在水中,液面上升的高度是物体A、B完全浸没液面上升高度的一半,即此时液面上升高度为
由题意可知,A、B之间绳子的长度为
当B接触容器底部,A下表面到容器底部的距离为
A下表面到液面的距离为
则当B接触容器底部时,水对A下表面的压强
答:(1)物体B的重力为;
(2)物体B的密度为;
(3)当B接触容器底部时,水对A下表面的压强为。
11.(1)4N (2)4×10-4 m3 (3)1.25×103kg/m3 (4)2.5×103 Pa
【详解】解:(1)由F-t图像可知当t=2s时,圆柱体刚好离开水面,此时弹簧测力计的示数等于圆柱体的重力
G=F示=5N
当t=0s时,圆柱体刚好浸没水中,弹簧测力计的示数
F示′=G-F浮=1N
则圆柱体受到的浮力
F浮=G-F示′=5N-1N=4N
(2)根据阿基米德原理圆柱体浸没在水中时,圆柱体的体积
(3)圆柱体的质量
圆柱体的密度
(4)由图丙得出,在2s内圆柱体上升的路程为0.2m,即圆柱体的高h=0.2m,圆柱体的底面积
圆柱体对水平桌面的压力为圆柱体的重力,圆柱体对水平桌面的压强
答:(1)圆柱体浸没在水中时受到的浮力大小为4N;
(2)圆柱体的体积为4×10-4m3;
(3)圆柱体的密度为1.25×103kg/m3;
(4)圆柱体竖直放置在水平桌面时对桌面的压强为2500Pa。
12.(1);(2);(3)6×10-4m3
【详解】解:(1)因为正方体木块浸没水中,所以正方体木块排开水的体积
V排=V木=(0.1m)3=10-3m3
木块受到的浮力
F浮=ρ水V排g=1.0×103kg/m3×10-3m3×10N/kg=10N
(2)木块的重力
G木=ρ木gV木=0.6×103kg/m3×10N/kg×10-3m3=6N
因为木块静止,所以木块受到的浮力
F浮=G木+F拉
细线的拉力
F拉=F浮-G木=10N-6N=4N
(3)因为
F浮>G木
所以剪断后木块上浮,最后漂浮,则木块静止时受到的浮力
F浮′=G木=6N
木块静止时排开水的体积
答:(1)木块所受的浮力是10N;
(2)细线的拉力是4N;
(3)剪断细线后,木块静止时排开水的体积是6×10-4m3。
答案第1页,共2页
答案第1页,共2页
1.如图所示,两个完全相同的底面积为100cm2的轻质薄壁圆柱形容器A、B放在水平桌面上(容器足够高),另有两个完全相同的圆柱体甲、乙,其底面积为50cm2。A中盛有质量为5kg的水,B中放置圆柱体乙,(g取10N/kg)求:
(1)容器A中水的重力;
(2)水对容器A底部的压强p;
(3)若通过两种方法分别增大容器对水平桌面的压强和液体对容器底部的压强,并测出容器对水平桌面的压强变化量 p容、水对容器底部的压强变化量 p水,如下表所示。
方法 容器对水平桌面的压强变化量 p容(帕) 水对容器底部的压强变化量 p水(帕)
① 6000 3000
② 5000 8000
方法a:圆柱体甲放入盛有水的容器A中。
方法b:向放置圆柱体乙的容器B加入质量为5千克的水。
请根据表中的信息,通过计算判断方法a、b与表中方法①、②的对应关系,并求圆柱体甲、乙的密度。
2.如图所示,水平地面上有一底面积为1.5×10-2m2的圆柱形容器。容器中水深40cm,一个边长为10cm的正方体物块通过一根细线与容器底部相连,细线受到的拉力为4N。求:
(1)此时容器底受到水的压强和压力;
(2)此时物块受到的浮力;
(3)细线剪断后,物块静止时浸入水中的体积。
3.有两个不吸水的圆柱体A和圆柱体B,A的顶部系有一根轻质细线。已知A的质量为1.32kg,密度为1.1×103kg/m3,高为12cm,B的底面积为40cm2,求:
(1)A的底面积为多少cm2;
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,求A对B的压强;
(3)将A竖直放入薄壁柱形容器中,向容器中缓慢加入液体直至加满。液体体积与深度的关系如图所示。然后用细线将A竖直向上提升3cm,细线的拉力为6.3N,液体对容器底部的压力减小,求该液体的密度。(圆柱体A始终处于竖直状态)
4.图甲为研究匀速直线运动的实验装置,一个半径为2cm的球由于磁铁的吸引静止在盛水的玻璃管底,水深1m,移除磁铁后,球在玻璃管中上升,图乙为球在露出水面前运动速度与时间的关系图像,其中v0=0.05m/s,水的密度为1.0×103kg/m3,求:
(1)移除磁铁前,玻璃管底受到水的压强;
(2)球在玻璃管上升过程中前4s的平均速度;
(3)已知球上升时受到水的阻力与其速度的关系为f=kv,球的体积用V,水的密度用ρ0表示,请推导球的密度表达式(用字母表示)。
5.如图甲所示,弹簧测力计下端悬挂着一个实心圆柱体Q,圆柱体Q浸没在盛水的大水槽中,现将测力计缓缓提升,直到圆柱体Q全部露出水面一段距离,在该过程中弹簧测力计的示数F随圆柱体上升高度h的关系如图乙所示,水槽内水面的变化忽略不计。求:
(1)圆柱体浸没时受到的浮力。
(2)圆柱体的底面积。
(3)将物块P与圆柱体Q用细线连接放入水槽内,二者恰好悬浮,如图丙所示:如果物块P的体积为400cm3,求物块P的密度。
6.小虎同学研究弹簧测力计的示数F与金属块A下表面离液面的距离h的关系,实验装置如图甲所示。用弹簧测力计提着金属块A,使其缓慢浸入酒精中(ρ酒精=0.8×103kg/m3且液体未溢出,g=10N/kg),得到F与h的关系图象如图乙所示。请计算:
(1)金属块A完全浸没在液体受到的浮力;
(2)金属块A的密度;
(3)金属块A的底面积。
7.2022年5月15日凌晨1点26分,中国自主研发的“极目一号”III型浮空艇从海拔4270m的科考营地顺利升空,如图甲所示,4点40分达到9032m,超过珠峰8848.86m的高度,创造浮空艇大气科学观测世界纪录。已知浮空艇体积约为9000m3,总质量约为2.6t。求:
(1)浮空艇受到的重力;
(2)已知科考营地的空气密度约为0.8kg/m3,此时浮空艇受到的浮力;
(3)为了有效控制浮空艇,用缆绳将其系在一辆质量为90t的锚泊车上,如图乙所示。浮空艇未升空时,缆绳处于竖直拉直状态且重力忽略不计,锚泊车对地面的压力。
8.放在水平桌面上的薄壁圆柱形容器重8N,底面积0.01 m2,弹簧测力计的挂钩上挂着一物块,现将物块从水面上方以恒定的速度下降,直至全部没入水中,容器内水的 深度由16cm升高到20cm,如图甲所示,图乙是绳子的拉力随时间t变化的图象,若不 计水的阻力(ρ水=1.0×103kg/m3),(g取 10N/kg)求:
(1)物块未放入水中时,容器底受到的水的压强;
(2)物块浸没在水中时受到的浮力;
(3)物块的密度;
9.如图所示,用轻质的细线将边长为10cm,质量为600g的正方体A和体积为的球体B相连接后轻轻地放入水中,两物体最终静止时恰好在水中处于悬浮状态,此时正方体A上表面到水面的距离为12cm()。求:
(1)将正方体A看成一个有质量的点,如图乙所示,请在图乙中画出正方体A的受力示意图;
(2)正方体A上表面所受水的压力大小;
(3)球体B的密度大小。
10.如图甲所示,A、B为不同材料制成的体积相同的实心正方体,物体A的质量为0.8 kg,圆柱形容器的底面积是A或B下表面积的4倍。B的下表面刚好在水面上,现沿竖直方向将A、B缓慢放入水中,直到B接触容器底部。上端绳子的拉力是F,F随B下降的距离h变化的图像如图乙所示。绳的质量和体积忽略不计。求:
(1)物体B的重力;
(2)物体B的密度;
(3)当B接触容器底部时,水对A下表面的压强。
11.小明用弹簧测力计拉着一圆柱体从水中匀速竖直向上运动,如图乙和如图丙分别记录的是圆柱体恰好运动到如图甲所示位置以后的0~6s时间内,弹簧测力计的示数随时间变化的F-t图象和圆柱体运动的路程随时间变化的s-t图象(不计水的阻力和柱体表面沾水的影响,g取10N/kg)求:
(1)圆柱体浸没在水中时受到的浮力大小;
(2)圆柱体的体积;
(3)圆柱体的密度;
(4)圆柱体竖直放置在水平桌面时对桌面的压强。
12.如图所示,一边长为,密度为的正方体木块,将它用细线系于某容器的水中,()。求:
(1)木块所受的浮力;
(2)细线的拉力;
(3)剪断细线后,木块静止时排开水的体积。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)50N;(2)5000Pa;(3)方法b与②对应,则方法a与①对应,2×103kg/m3
【详解】解:(1)容器A中水的重力为
(2)水对容器A底部的压力为
水对容器A底部的压强为
(3)方法b:向放置圆柱体乙的容器B加入质量为5kg的水,容器对桌面的压强变化量为
所以,方法b与方法②对应,则方法a与①对应。
方法a:圆柱体甲放入盛有水的容器A中,容器对水平桌面的压力变化量为
则圆柱体的质量为
方法a:圆柱体甲放入盛有水的容器A中,因圆柱体对水的压力和水对圆柱体的浮力是一对相互作用力,所以,圆柱体受到的浮力为
由前面的计算可知,圆柱体的重力为50N,浮力小于重力,故圆柱体沉底,所以,在物体完全浸没时,圆柱体的体积和排开水的体积相等,所以,圆柱体的体积是
圆柱体的密度为
答:(1)容器A中水的重力50N;
(2)水对容器A底部的压强p是5000Pa;
(3)通过计算判断方法b与②对应,则方法a与①对应,圆柱体甲、乙的密度是2×103kg/m3。
2.(1),60N;(2)10N;(3)。
【详解】(1)容器底受到水的压强
水对容器底的压力为
(2)木块的体积
木块浸没在水中时受到的浮力
(3)物体受到竖直向下的重力和拉力、竖直向上的浮力,处于静止状态,则物体的重力为
因为木块浸没在水中时的浮力大于木块的重力,所以剪断细线后,木块会上浮直至漂浮在水面上,由于木块漂浮,木块受到的浮力
由得此时排开水的体积浸入水中的体积
答:(1)此时容器底受到水的压强为4000Pa,压力为60N;
(2)此时物块受到的浮力为10N;
(3)细线剪断后,物块静止时浸入水中的体积为。
3.(1)100;(2)3.3×103Pa;(2)1.4×103kg/cm3
【详解】解:(1)已知物体A的质量和密度
mA=1.32kg,ρA=1.1×103kg/m3
则A的体积
又A的高度
hA=12cm=0.12m
所以A的底面积
(2)将B竖直放在水平桌面上,再将A竖直放在B的正上方,由于A的底面积大于B的底面积,因此,此时受力面积为
SB=40cm2=4×10-3m2
A对B的压强
(3)结合图像可知
,
故可得
已知SA=100cm2,故容器底面积
S容=3SA=3×100cm2=300cm2
用细线将A竖直向上提升3cm,因为液体对容器底部的压力减小,所以可判断此时液面下降了,说明物体A是漂浮状态,物体A的重力
GA=mAg=1.32kg×10N/kg=13.2N
当细绳拉着物体A向上移动h=3cm后,细线的拉力F=6.3N,则此时物体A的浮力
F浮′=G-F=13.2N-6.3N=6.9N
设液面下降的高度为h,则物体A排开液体的体积变化量
V排=SA(h+h)=S容h
带入已知量可得
V排=1×10-2m2×(h+0.03m)=3×10-2h
解得
h=0.015m,V排=4.5×10-4m3
浮力的变化量
F浮=13.2N-6.9N=6.3N
则液体密度
答:(1)A的底面积为100cm2;
(2)A对B的压强为3.3×103Pa;
(3)该液体的密度为1.4×103kg/cm3。
4.(1)1×104Pa;(2)0.0275m/s;(3)
【详解】解:(1)移除磁铁前,水深h=1m,所以玻璃管底受到水的压强
p=ρgh=1.0×103kg/m3×10N/kg×1m=1×104Pa
(2)由图可知,球在露出水面前运动的时间为21s,根据可得,4~21s球上升的距离
s0=v0t=0.05m/s×17s=0.85m
则球在玻璃管上升过程中前4s上升的距离
s′=s-s0=1m-0.85m-2×0.02m=0.11m
所以球在玻璃管上升过程中前4s的平均速度
(3)由图可知,球4~21s时匀速上升,受力平衡,所以有
G+f=F浮
即
解得球的密度
答:(1)玻璃管底受到水的压强是1×104Pa;
(2)球在玻璃管上升过程中前4s的平均速度0.0275m/s;
(3)球的密度表达式。
5.(1)2.0N;(2)4×10﹣4m2;(3)0.6×103kg/m3
【详解】解:(1)由图乙知,当上升高度在20cm以上,圆柱体脱离水面,弹簧测力计示数F=2.0N,此时圆柱体处于空气中,圆柱体Q的重力为
由图乙知,圆柱体上升高度在0~10cm时,圆柱体Q浸没在水中,根据称重法可知,Q所受到的浮力为
(2)由阿基米德原理可得圆柱体Q的体积为
由图乙知,上升10cm时圆柱体上表面与水面恰相平,上升20cm时圆柱体恰好全部露出水面,所以圆柱体高度为
圆柱体的底面积为
(3)图丙中物块P和与圆柱体Q悬浮在水中,则P、Q排开水的体积为
P、Q所受的总浮力为
根据悬浮体积可知:P、Q的总重力为
则P的重力为
P的质量为
所以P的密度为
答:(1)圆柱体的重力为2.0N;
(2)圆柱体的底面积为4×10﹣4m2;
(3)将物块P与圆柱体Q用细线连接放入装水容器内,二者恰好悬浮如图丙所示。如果物块P的体积为400cm3,则物块P的密度为0.6×103kg/m3。
6.(1)4N;(2)2×103kg/m3;(3)100cm2
【详解】解:(1)由图知,当h1=0时,弹簧测力计的示数为10N,即物体A的重力G=10N,完全浸没在液体中时,排开液体的体积不变,根据阿基米德原理可知,受到的浮力不变,由F浮=G-F可知,测力计示数不变,故由图象可知物体的高度h=5.0cm;A浸没时受到液体的浮力
F浮=G-F=10N-6N=4N
(2)根据阿基米德原理可知物体所受的浮力
F浮=ρ酒精gV排=ρ酒精gV物
金属块A的体积
①
金属块A的密度
②
由①②得:金属块A的密度
(3)金属块A的底面积是
答:(1)金属块A完全浸没在液体受到的浮力为4N;
(2)金属块A的密度为2×103kg/m3;
(3)金属块A的底面积为100cm2。
7.(1)2.6×104N;(2)7.2×104N;(3)8.54×105N
【详解】解:(1)浮空艇受到的重力为
G艇=m艇g=2.6×103kg×10N/kg=2.6×104N
(2)此时浮空艇受到的浮力
F浮=ρ空气gV排=ρ空气gV=0.8kg/m3×10N/kg×9000m3=7.2×104N
(3)浮空艇未升空时,缆绳处于竖直拉直状态,此时浮空艇受到向下的重力和拉力、向上的浮力作用,根据力的平衡条件可知绳子的拉力
F拉=F浮﹣G艇=7.2×104N﹣2.6×104N=4.6×104N
锚泊车的重力为
G车=m车g=90×103kg×10N/kg=9×105N
锚泊车受竖直向下的重力、竖直向上的拉力和支持力作用,则地面对车的支持力为
F支=G车﹣F拉=9×105N﹣4.6×104N=8.54×105N
由于物体间力的作用是相互的,则锚泊车对地面的压力
F压=F支=8.54×105N
答:(1)浮空艇受到的重力为2.6×104N;
(2)此时浮空艇受到的浮力为7.2×104N;
(3)锚泊车对地面的压力为8.54×105N。
8.(1)1600Pa;(2)4N(3)2.5×103kg/m3
【详解】(1).物块未放入水中时,容器底受到的水的压强:
p=ρgh=1.0×103kg/m3×10N/kg×0.16m=1600Pa;
(2).物块浸没后,水的深度增加量:
△h=20cm 16cm=4cm=0.04m,
物块浸没在水中时物体排开水的体积:
V排=V物=S△h=0.01m2×0.04m=4×10 4m3,
物块受到的浮力:
F浮=ρgV排=1.0×103kg/m3×10N/kg×4×10 4m3=4N;
(3).由图乙可知,物块的重力G=F=10N,
物块的质量:m== =1kg,
物块的密度:ρ物= ==2.5×103kg/m3
答:(1).物块未放入水中时,容器底受到的水的压强为1600Pa;
(2).物块浸没在水中时受到的浮力为4N;
(3).物块的密度为2.5×103kg/m3;
9.(1) ;(2)12N;(3)
【详解】解:(1)对A进行受力分析A受到竖直向上的浮力,竖直向下的重力和拉力,如图所示:
(2)正方体A上表面所处的深度为
正方体A上表面所受水的压强
接触面积为
正方体A上表面所受水的压力大小为
(3)正方体A的体积为
正方体A和球体B浸入液体的总体积为
因为正方体A和球体B这个整体在水中悬浮,所以总重力等于浮力,故总重力为
A和B的总质量为
球体B的质量为
球体B的密度大小为
答:(1)将正方体A看成一个有质量的点,正方体A的受力示意图为;
(2)正方体A上表面所受水的压力大小为12N;
(3)球体B的密度大小为。
10.(1);(2);(3)
【详解】解:(1)物体A的重力
当h=0时,绳子的拉力大小等于物体A、B的重力之和,由图可知,当h=0时,拉力大小F0=50N,则物体B的重力为
(2)由图可知,绳子的拉力最后变为30N不变,此时物体A、B完全浸没在水中,浮力不变,此时物体A、B所受浮力之和为
物体A、B排开水的体积为
物体A、B的体积相同,所以物体B的体积为
物体B的质量
物体B的密度为
(3)物体A、B的边长为
由图可知,当h=30cm时,B接触容器底部,所以原来烧杯中水的深度为30cm,A、B的底面积为
烧杯的底面积
当A、B完全浸没以后,液面上升的高度为
当A、B完全浸没以后,烧杯中水的深度为
由图可知,当h=11.5cm时,绳子的拉力第二次减小,说明此时物体A开始进入水中,此时只有B浸没在水中,液面上升的高度是物体A、B完全浸没液面上升高度的一半,即此时液面上升高度为
由题意可知,A、B之间绳子的长度为
当B接触容器底部,A下表面到容器底部的距离为
A下表面到液面的距离为
则当B接触容器底部时,水对A下表面的压强
答:(1)物体B的重力为;
(2)物体B的密度为;
(3)当B接触容器底部时,水对A下表面的压强为。
11.(1)4N (2)4×10-4 m3 (3)1.25×103kg/m3 (4)2.5×103 Pa
【详解】解:(1)由F-t图像可知当t=2s时,圆柱体刚好离开水面,此时弹簧测力计的示数等于圆柱体的重力
G=F示=5N
当t=0s时,圆柱体刚好浸没水中,弹簧测力计的示数
F示′=G-F浮=1N
则圆柱体受到的浮力
F浮=G-F示′=5N-1N=4N
(2)根据阿基米德原理圆柱体浸没在水中时,圆柱体的体积
(3)圆柱体的质量
圆柱体的密度
(4)由图丙得出,在2s内圆柱体上升的路程为0.2m,即圆柱体的高h=0.2m,圆柱体的底面积
圆柱体对水平桌面的压力为圆柱体的重力,圆柱体对水平桌面的压强
答:(1)圆柱体浸没在水中时受到的浮力大小为4N;
(2)圆柱体的体积为4×10-4m3;
(3)圆柱体的密度为1.25×103kg/m3;
(4)圆柱体竖直放置在水平桌面时对桌面的压强为2500Pa。
12.(1);(2);(3)6×10-4m3
【详解】解:(1)因为正方体木块浸没水中,所以正方体木块排开水的体积
V排=V木=(0.1m)3=10-3m3
木块受到的浮力
F浮=ρ水V排g=1.0×103kg/m3×10-3m3×10N/kg=10N
(2)木块的重力
G木=ρ木gV木=0.6×103kg/m3×10N/kg×10-3m3=6N
因为木块静止,所以木块受到的浮力
F浮=G木+F拉
细线的拉力
F拉=F浮-G木=10N-6N=4N
(3)因为
F浮>G木
所以剪断后木块上浮,最后漂浮,则木块静止时受到的浮力
F浮′=G木=6N
木块静止时排开水的体积
答:(1)木块所受的浮力是10N;
(2)细线的拉力是4N;
(3)剪断细线后,木块静止时排开水的体积是6×10-4m3。
答案第1页,共2页
答案第1页,共2页
